はじめに
あるデータを回帰分析したいとします。極単純なデータであれば線形回帰で十分ですが、データが線形に並んでいなかったり、誤差が正規分布に従っていない場合は、線形回帰では予測誤差が大きくなってしまいます(線形回帰を最小二乗法で実施する場合は誤差が正規分布であることを仮定しています。)。
そこで、自身で回帰曲線を与えたり、誤差構造を与えたりできるモデルとして一般化線形モデル(以下、GLM)を使用します。
参考
環境
- macOS Majave 10.14.3
- statsmodels==0.9.0
手順
GLMの基本
GLMは線形予測子、リンク関数、誤差構造という3つの要素によって成り立っています。ぞれぞれ意味を説明します。
目的変数を$y$、説明変数を$x_i$とします。リンク関数を$\psi$としたとき、説明変数と誤差を含まないな目的変数の間に、次の関係が成り立つとします。
\psi(\hat y) = \sum_{i=0}^{M}w_i \phi_i(x)
この右辺の式を線形予測子といいます。
具体的なリンク関数と線形予測子を与えて、意味を見てみましょう。
説明変数は1変数とします。リンク関数$\psi(\hat y)$を$\log \hat y$として、線形予測子を$ \phi_i(x)=x^i$、$M=1$とします。すると上の式は次のようになります。
\log \hat y = w_0 + w_1 x
これを少し書き換えて$y=$の形にしてやります。すると次のようになります。
\hat y = e^{w_0 + w_1 x}
これは回帰モデルが$e$の肩に乗った式になっています。したがって、このモデルによる予測値は指数関数の曲線のような値になります。線形回帰モデルでは直線の予測しかできなかったのに対し、このモデルでは曲線の予測ができるようになっています。
このように、リンク関数は予測曲線の構造を決め、線形予測子は説明変数$x_i$が予測にどのように効くのかを決定します。
誤差構造はyが従う分布のことです。上の例で考えた式$y(x)$に対し、ある$x$を固定したときの$y(x)$の分布を決定します。
例えば誤差構造を平均$\lambda$のポアソン分布としてみましょう。このポアソン分布は、入力$x$に対する $\hat y(x)=e^{w_0 + w_1 x}$の値を平均値とした$y$の分布なので、$\lambda = e^{w_0 + w_1 x}$となります。最終的に$y$の分布は次のように書けます。
y \sim p(y|\lambda) \\
p(y|\lambda) = \frac{\lambda^y e^{-\lambda}}{y!} \\
\lambda = e^{w_0 + w_1 x}
これでモデルが出来ました。あとは最尤推定法でデータ$x_n, t_n$に対し、尤度$L = \prod_n p(t_n|\lambda(x_n, w))$を最大化するような$w$を求めれば良いことになります。
求めた$w$を代入した$\hat y = e^{w_0 + w_1 x}$が予測式になります。
細かい話
もう少しちゃんとした話をします。
一般化線形モデルは本来、目的変数$y$を指数型分布族で捉えようとするモデルです。指数型分布族は次のように表せる確率密度関数です。
p(y|\theta, \varphi) = \exp\left[\frac{y \theta -a(\theta)}{\varphi} + c(y, \varphi)\right]
この分布の平均値は$\mu = a'(\theta)$、分散は$V = \varphi a''(\theta)$です。この時点では入力$\mathbf{x}$は登場していません。
入力$\mathbf{x}$と$y$を結びつけるには、$y$の平均値を$\mathbf{x}$の式でモデリングしてやれば良いです。そこで、$y$の平均値$\mu = a'(\theta)$が$\theta$に依存することを考慮し、$\theta$と$\mathbf{x}$を結びつけるための、逆関数を持つ単調関数$g(\theta) = \mathbf{w^\top \phi(x)}$を考えます。こうして与えられた$\left(p(y|\theta, \varphi), g(\theta), w^\top \phi(x)\right)$の3要素を持ったモデルのことを一般化線形モデルと呼びます。
これによって、$y$の平均値は$\mu = a'(g^{-1}(\mathbf{w^\top \phi(x)}))$で与えられます。$\psi^{-1} = a'g^{-1}$と書いたときの$\psi$をリンク関数と呼びます。$g$を選ぶことで、予測曲線を決定します。特に$g$を恒等関数に取ったリンク関数を正準リンク関数と呼びます。
ポアソン分布のときは、指数型分布族の定義式とポアソン分布の密度関数を比べることで下記の対応がすぐに分かります。
\begin{align}
\varphi &= 1 \\
\theta &= \log \lambda \\
a(\theta) &= e^\theta \\
c(y) &= -\log y!
\end{align}
これから正準リンク関数が$\psi(\theta) = \log\theta$であることがわかります。
statsmodelを使ったモデル作成
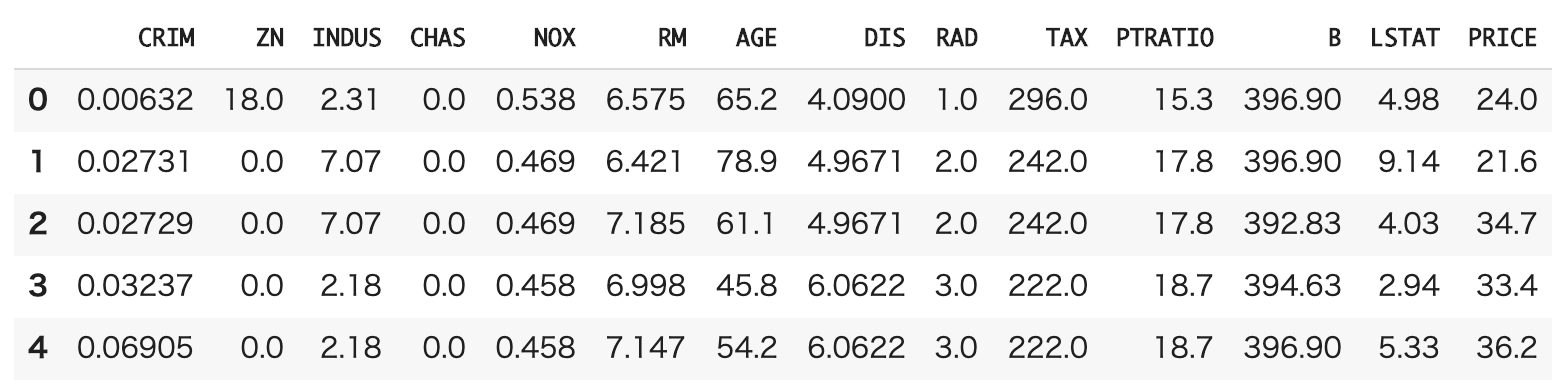
ボストン市の住宅価格データ(https://pythondatascience.plavox.info/scikit-learn/scikit-learn%E3%81%AB%E4%BB%98%E5%B1%9E%E3%81%97%E3%81%A6%E3%81%84%E3%82%8B%E3%83%87%E3%83%BC%E3%82%BF%E3%82%BB%E3%83%83%E3%83%88)を用いてGLMを試してみます。
ただし、以下では使い方を確認するにとどめ、チューニングなどは行いません。(GLM用に良いデータが有ればちゃんとやってみます)
statsmodelで使用できる誤差構造とリンク関数の組み合わせは下記のとおりです。
| 誤差構造 | リンク関数 | 使えると書いてないけどエラーにならないリンク関数 |
|---|---|---|
| Poisson | identity, log, sqrt | |
| Binomial | identity, log, cauchy, logit, probit, cloglog | |
| Gamma | identity, log, inverse_power | |
| Gaussian | identity, log, inverse_power | |
| InverseGaussian | identity, log, inverse_power, inverse_squared | |
| NegativeBinomial | identity, log, cloglog, nbinom, Power | sqrt, inverse_power, inverse_squared |
| Tweedie | identity, log, Power | sqrt, inverse_power, inverse_squared |
まずはデータを読み込みトレーニングとテストに分けます。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['PRICE'] = boston.target
X = df.drop('PRICE', axis=1)
y = df['PRICE']
# テータ分割
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size =0.8)
statsmodels.apiでリンク関数と誤差関数を、statsmodels.formula.apiでGLMモデルを使用します。
import statsmodels.api as sm
import statsmodels.formula.api as smf
# 説明変数と目的変数を一つの行列にする必要あり
data = pd.concat([X_train, y_train], axis=1)
# 線形予測子を定義
formula = "PRICE ~ 1 + INDUS + CHAS + RM + RAD"
# リンク関数を選択
link = sm.genmod.families.links.log
# 誤差構造を選択
family = sm.families.Poisson(link=link)
mod = smf.glm(formula=formula, data=data, family=family )
result = mod.fit()
print(result.summary())
モデルの評価方法はいくつかあると思いますが、AICはすぐに計算できて便利です。
# AIC
result.aic
予測はpredictメソッドを使用します。
y_pred = result.predict(X_test)
おわりに
今回は一般化線形モデルについて見てきました。一般化線形モデルは統計モデルなので、予測モデルがよく当てはまった場合、その誤差構造などから現象に潜むミクロな構造がわかるかもしれません。モデルを通して、なぜ変数がこのようなモデルによって説明できるのか考えるのが楽しくなると思います。