2024/04/19追記
普段は「通知が迷惑かなー」と思ってブックマークしていただいている方に通知せず記事を編集しているのですが、この記事をブクマしていただいている方は続きが気になっている方だと思いますので通知させていただきます。
結論から言うと、この記事を読んだ @pocokhc (ちぃがぅ)さんという方が金子勇さんが書いたED法のサンプルプログラムを見つけてくださいました。
ちぃがぅさんの記事はこちら
自分で解明したかったという気持ちも無いことは無いですが、バズった時点で誰かが実装してくれそうな気はしていました。新卒からIT業界に入って4年目が始まったところですが、業務以外で初めて業界にコントリビュートできた気がして嬉しいです！
追記ついでに、謝罪します。初回公開時に記事タイトル含め本文中で何か所か「Winney」と書いてしまっていた箇所がありました。失礼いたしました。誤字修正してあります。指摘してくださった何人かの方に感謝申し上げます。
はじめに
今更ですが映画『winny』を見ました。
劇中で、金子勇さんのセリフにED法という聞いたことのないアルゴリズムが登場しました。
『このNekoFightにはAIを搭載しています。AIの方式は単なる3層ニューラルネットで、学習アルゴリズムは私独自のED法です。
ED法は、バックプロパゲーションが実際の神経系のメカニズムとしてはありえないというのが気になって私の方で考え出した学習アルゴリズムですが、 学習速度が非常に速いのと、中間層を増やせば無制限に性能が上がるのが特徴のアルゴリズムです。』
(『Winny』, 2023年, 監督・脚本：松本優作)
彼が作っていたNekoFightというゲームのAIに使われているアルゴリズムのようで、ダウンロードページにセリフと同じ内容が書いてありました。
ED法について気になりネットで調べていると、下記の記述を見つけました。
ED法は、実際のヒトの脳の動きをシミュレーションする、金子さん独自のアルゴリズムです。論文もソースコードもないため、残念ながらどのように実装されているのか、分かっていませんが、2009年に開催された『第参回天下一カウボーイ大会』でプレゼンした映像がYoutubeに登録されています。(金子勇とWinnyの夢を見た 第6話 フリーソフト：https://note.com/fukuy/n/nfca21224eedc)
ED法は金子さんが考案したアルゴリズムで、論文やソースコードは無く、どのように実装されているのか分かっていないようです…
唯一の資料であるスライド発表を解読する
論文やソースコードなどが残っていないため、私がアクセスできる唯一の手掛かりは金子さんがED法について発表している上記の動画だけになります。この動画を詳細に観ていきましょう。
発表のコンセプト(動画冒頭~3:27)
挨拶のパートです。映画でも少し触れられていた、金子さんのユーモラスな一面が垣間見えます。
発表のタイトルは 『実際の神経系からヒントを得た新型人工知能モデル』。
ファイル共有ソフト『winny』で有名になった金子さんですが、ご専門はシミュレーションだそうです。発表では、「本物の脳みそを作ってやろう」 とおっしゃっています。
ニューラルネットワークについて(3:28~4:28)
最もポピュラーな脳のシミュレーションである、ニューラルネットワークについて紹介するパートです。
金子さんは「知っているというもので話します。」と言ってあまり詳細に語っていなかったので、ご存知無い方のために少し捕捉します。
ニューラルネットワークについての捕捉解説
脳の中にはニューロンと呼ばれる細胞が無数にあり、ニューロンどうしはお互いにつながり合って巨大なネットワークを作っています。
外界からの刺激を受けて、ニューロンは電気刺激を他のニューロンに伝えます。受け取ったニューロンは、その刺激がある閾値を超えると発火してさらに次のニューロンに刺激を伝えます。この連続で、ニューラルネットワークは複雑な情報処理を行っています。
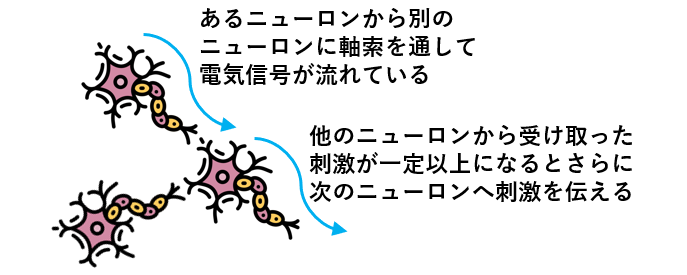
上記のニューロンの働きを、数理モデル化したものがニューラルネットワークです。
外界からの刺激を受けて発火したニューロンをX、Xからの電気刺激を受けるニューロンをY、XとYをつなぐ軸索をWと置いています。
Yが受ける刺激の強さは、XとYをつなぐ軸索Wの太さ(太いほど刺激を良く伝える)で決まると考えて、もともとの刺激の大きさXと、軸索の太さWをかけた値がYに伝わります。
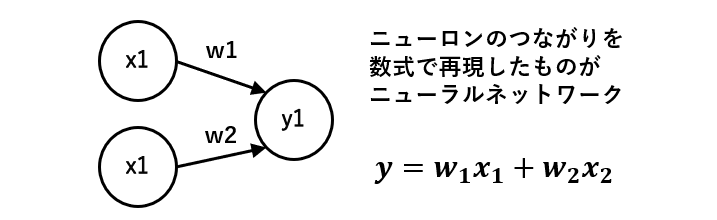
ニューラルネットワークを使ったAIは、一般的にWの値を調整することで入力Xに応じた適切なYを出力するように設計されています。
出力されたYを入力としてもう一度同じことを繰り返すと金子さんが作った3層ニューラルネットワークになります。最初に引用した『Winny』劇中のセリフで、
中間層を増やせば無制限に性能が上がる
とありますが、これは3層ニューラルネットワーク一般に言える普遍性定理のことでしょう。
普遍近似定理 (Cybenko (1989)など)
ニューラルネットワークは、⼗分な数のパラメタがあれば、連続関数を任意の精度で近似できる。
金子さんはバックプロパゲーションが嫌いという話(4:29~5:52)
バックプロパゲーション（誤差逆伝搬法）というのはWの値を調整する方法として最もポピュラーなアルゴリズムです。
金子さんはこのアルゴリズムが大嫌いだそうで、このパートではなぜ嫌いかについて力説しています。動画ではバックプロパゲーションについても詳しい説明は無いため捕捉しておきます。
バックプロパゲーションについての補足解説
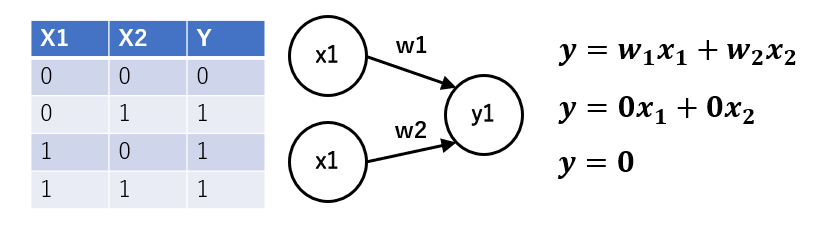
入力が二つで出力が一つの単層ニューラルネットワーク(下図)を使ってオアゲートを実装したいとします。
Wの初期値を0とすると、入力Xの値によらずYには0が出力されます。
※通常Wはランダムな値に初期化されますが、今回は簡単のために0としています。
どんな入力がきても0が出力されるゲートを、オアゲートに変える(学習させる)ために次の操作を行います。
STEP1
X1=0, X2=0の場合には出力y1は0になります。この場合、すでにオアゲートとしての期待した動作になっているためWはどちらも0のままです。
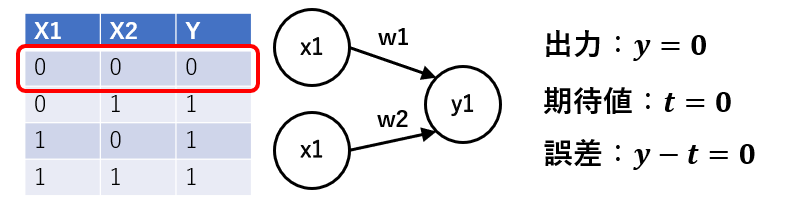
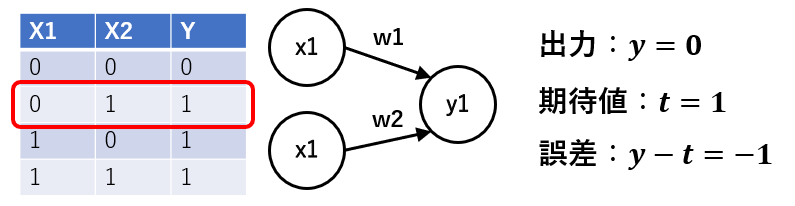
STEP2
X1=0, X2=1の場合にも当然出力y1は0になります。このとき、オアゲートとしては1を出力したいのに0が出力されているので、W2を少し大きくします。
例えば0.1を足してW2=0.1とすると、次にX1=0, X2=1が入力された時の出力は0.1になり、オアゲートの出力である1に少し近づきます。仮に出力が大きすぎる場合はWを少し減らします。
STEP3
STEP1, STEP2を全てのXの組み合わせに対して十分な回数行なった後、ニューラルネットワークがオアゲートとして振舞うようWが調整されているはずです。
この一連の手順を、バックプロパゲーションと呼びます。
※実際にはYを活性化関数に入れる必要がありそうですが、本題ではないため割愛。
既存のニューラルネットワークの詳細はこちら↓
ではなぜ金子さんはバックプロパゲーションが嫌いなのか
その理由はシンプルで、『絶対こんなことやれないですよ。本物では。』とのことです。
人間の神経系では勾配消失は起こらないですし、そもそも何層も前の脳細胞にどうやってフィードバックを渡すのかということでしょう。
そこで、嫌いなバックプロパゲーションの代替として金子さんが考え出したのがED法です。
本物の脳っぽくないから嫌いというのはシミュレーションが好きな金子さんの性格なら分かる気がしますが、そこで本物の脳っぽいアルゴリズムを考え出せるのが金子さんのすごいところですね。
※勾配消失についても捕捉しようかと思ったのですが、前提知識が色々あるので気になる方はリンクをご覧ください。すみません...
簡単に言うと、ニューラルネットワークの層が増えた時、手前の層では誤差がほとんど出なくなってWの更新が出来なくなるという問題です。
ED法の概要紹介(5:53~6:30)
- 日本語で言うと誤差拡散法
- バックプロパゲーションはエラーを後ろに渡すが、ED法はエラーを全体で共有している
- この話はここで初めてするので、ネットで調べても出てこない
という内容です。
ED法の図解(6:31~11:03)
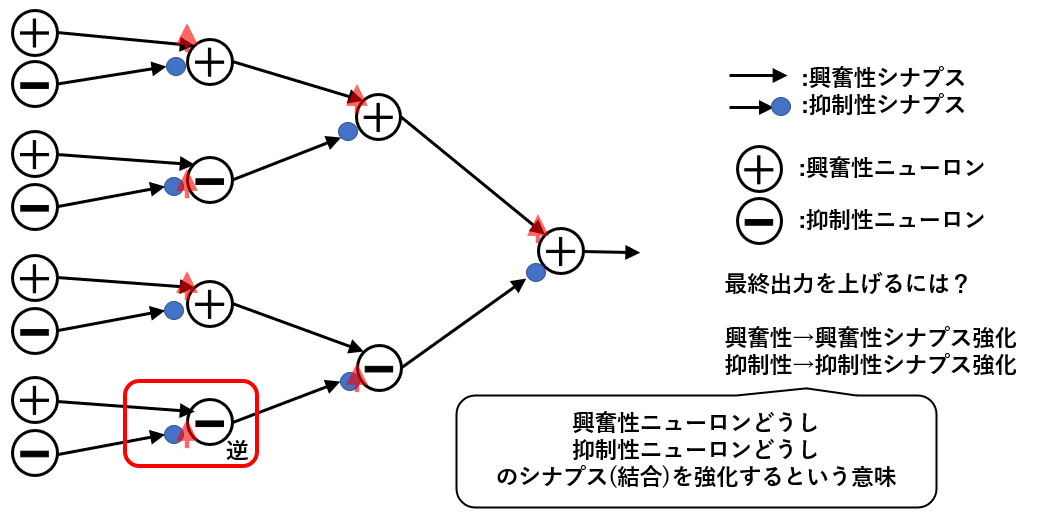
ED法のアイデアについて上記の図を使って解説しているパートです。
既存(当時)のニューラルネットワークは、各ニューロン(X)、シナプス(W)はどれも共通した性質をもっていましたが、このモデルでは興奮性ニューロンと抑制性ニューロンが用いられています。
学習のアルゴリズムとしては、
- 最終出力を上げたいときは、同じ種類のニューロンどうしの結合(図中赤い矢印)を強くする
- 最終出力を下げたいときは、違う種類のニューロンどうしの結合を強くする
という方法を取るそうです。
バックプロパゲーションのアルゴリズムは数学的には正しいかもしれないが、実際には有り得ないので大体の部分は参考にしつつ、出力側でのエラーを全部の層で○○しちゃえ（大事なところが聞き取れず。）というアイデアで考案されたとのことです。
そして、金子さんによると図の赤枠でかこまれた「逆」と書いてある箇所は上記の規則を満たさないそうです。しかし、『やってみると動くからいいじゃん』 とおっしゃっていました。映画ではよく確認せずに調書に署名してしまって裁判で不利な証拠として使われるシーンがありましたが、細かいことは気にしない性格みたいですね。
11:03以降
ベンチマークテストを行った結果既存のバックプロパゲーションより良い結果を得られたことや、強化学習への応用可能性についてのスライドのため、ED法の中身を知りたいというこの記事の目的からは外れるため解説しません。気になる方は元動画をご覧ください。
11:03以降に登場するヒントになりそうな情報としては、通常のニューラルネットワークはアミノ酸系ニューロンを参考にしているが、ED法ではモノアミン系ニューロンを参考にしている(元動画19:50あたり)というもののみだと思います。
金子さんによると、モノアミン系ニューロンは、神経伝達物質をドカッと周辺に拡散する(要検証)そうで、彼はこの動きが脳の学習に関わっているのではないかと見ているそうです。
ED法の中身についての仮説
ここからは私の推測です。
仮説1 - 各ニューロンは連続値ではなく二値をとる
通常のバックプロパゲーションによる学習を行うニューラルネットワークのことが大嫌いな金子さんの性格から考えてED法では各ニューロンは(0, 1)か、(-1, 1)の二値を取るよう設計するはずだと考えました。実際のニューロンも、入力となる刺激が閾値を超えると発火して次のニューロンに刺激を与え、閾値未満だと何もしません。
各ニューロンが二値を取り、連続値を取らないと仮定することで、ED法(誤差拡散法)という名前がついていることにも理由づけができます。 ED法というのはもともの人工知能関連の言葉ではなく、金子さんが初めて使った言葉でもありません。
一般的なED法といえば、各ピクセルの明るさが0(真っ黒)~255(真っ白) の値のいずれか値を持っている画像を0か255の二値の画像に変換するアルゴリズムです。この時、最も単純に考えると、対象のピクセルの明るさが閾値より低ければそのピクセルを0、高ければ255とすることを思いつきます。
しかし、それだと閾値付近の明るさを持つピクセルの情報が大きく失われてしまいます。それを解決するために、あるピクセルのもともと持つ明るさと、閾値との差 「誤差」 を隣接するいくつかのピクセルに渡すことで画像全体としては誤差の情報が失われなくなります。
連続値を二値に変換するという意味では金子さんがやっていることと同じであり、おそらく既存のED法から着想を得た命名だと思います。
また、ED法は学習速度が非常に速いのが特徴だそうですが、連続値を二値化して計算量を削減しもともとの誤差拡散法のように情報を何らかの方で失わせないことが可能だとしたらこの特徴も実現できそうです。
仮説2 - 二値は、(0, 1)ではなく(-1, 1)である
- 最終出力を上げたいときは、同じ種類のニューロンどうしの結合(図中赤い矢印)を強くする
- 最終出力を下げたいときは、違う種類のニューロンどうしの結合を強くする
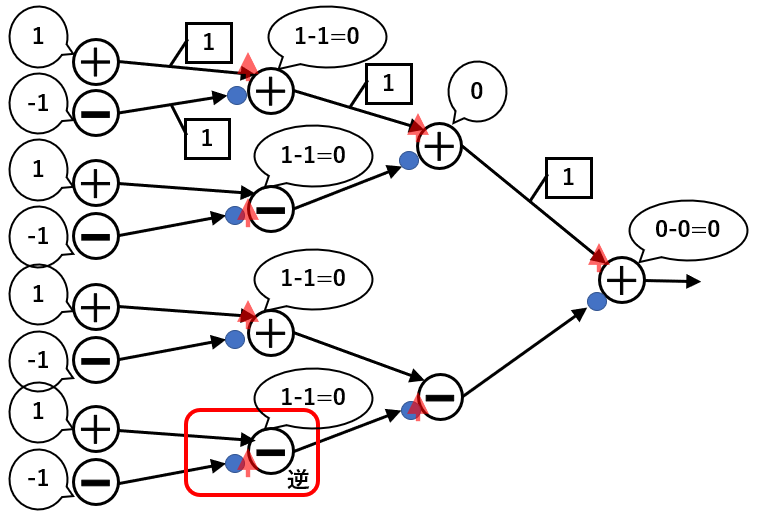
-1, 1にすると、ニューラルネットワークが上記のルールに従うためです。
例として、全てのWで初期値を1にして代入してみます。
この場合上のように各ニューロンの値によらず最終出力は0になります。
次に、同じ種類のニューロンどうしの結合を強くしてみます。通常のニューラルネットワークは0.1づつや、0.01づつ値を増やすことが多いですが、今回は簡単のために同じ種類のニューロンをつなぐWの値を+1して考えます。
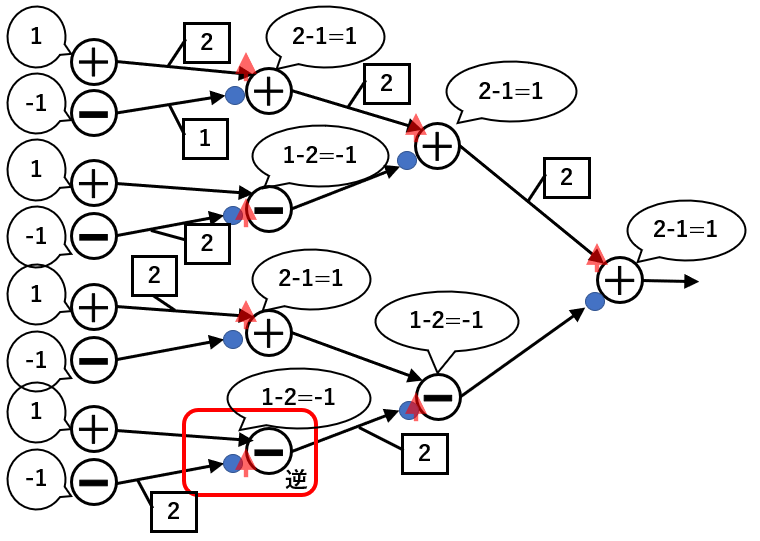
結果、最終出力は+1になり、ルール通り増えています。
逆に、違うニューロンどうしの結合を強めてみます。
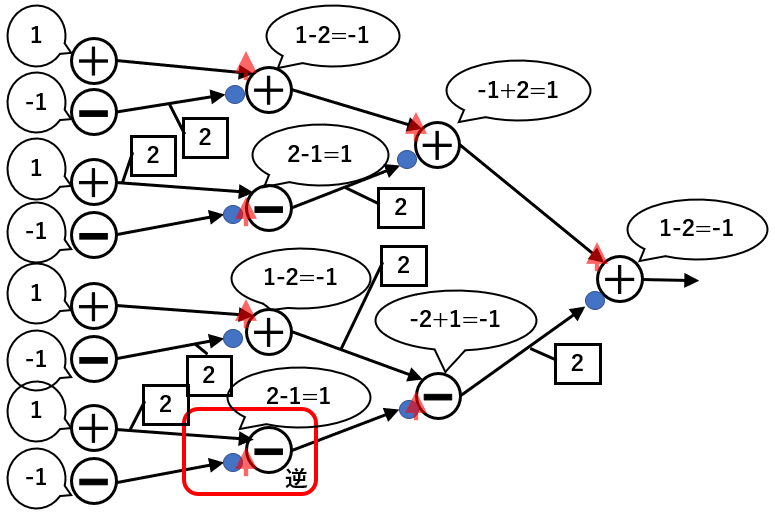
最終出力は-1になり、この場合もルール通り最終出力は減っています。
まとめ
仮説1, 2とも大枠は外していないと考えていますが、完璧にあっているというわけでもないと思います。スライド中の「逆」の意味については値を代入してみても良く分からなかったですし、ED法の名前の由来である誤差拡散法とのつながりも曖昧です。ED法を考えるうえで参考にしたという、モノアミン系ニューロンの働きについても知識不足です。
今回の記事では実際に実装を試みるところまではいけませんでしたが、今後、今回書ききれなかったいくつかのパターンも含めて実装してみて、ゆくゆくは完全解明を目指します。
もし情報をお持ちの方がいらっしゃいましたら、コメントで情報を提供いただけますと幸いです。