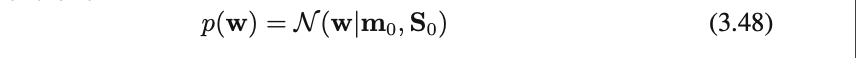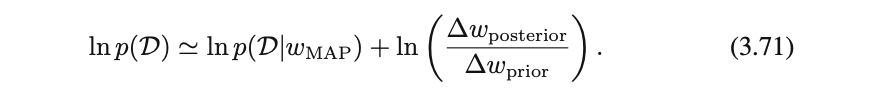#３.３ ベイズ線形回帰#
先週やった通り、線形回帰のパラメーターを最尤推定によって決める場合
・基底関数の数や形、正則化項によってモデルの複雑さが決まる
・↑の調整を失敗すると過学習を引き起こしたり、単純すぎるモデルになったりする
・データの一部を独立してテスト用データとして取っておき、テストすることで適切な調整ができるけど、計算量が大きい＆データの無駄遣い
ベイズ線形回帰なら、、、
過学習を回避し、訓練データだけからモデルの複雑さを自動的に決定できる！
##３.３.１ パラメーターの分布##
モデルパラメーター$w$の事前分布確率を導入しよう
前提ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
・目標変数$t$は一次元
・ノイズの精度パラメーター$β$は既知の定数
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
尤度関数・・・（3.1０）より, ガウス分布であり、指数にwの⼆次項のをもつ
事前分布・・・共役事前分布としてガウス分布（3.48）
事後分布・・・事後分布∝尤度関数×事前分布 なのでガウス分布
これまでに行ってきた計算を駆使すれば、(3.49)になるらしい
参考
P47：https://www.slideshare.net/aratahonda1/prml-3-33
Exercise 3.7：https://bicr.atr.jp//~mfukushima/PRML_resume.pdf
ただし
・事後分布はガウス分布なので、事後確率を最大にする重みベクトル$w$は、単純に$m_N$となる
・仮に無限に広い事前分布を考えると，事後分布の平均$m_N$は(3.15)で得られる最尤推定量 $w_{ML}$ と一致する
P49:https://www.slideshare.net/aratahonda1/prml-3-33
・そして$N = 0$ならば事後分布は事前分布に一致する．
ここで、議論を簡潔化するために、以降は事前分布を平均０，精度$α$の等方的ガウス分布で考える
対応する事後分布はかわらず（3.49）。ただし
ここで対数事後分布を求める
対数事後分布 ＝ 対数尤度 ＋ 対数事前分布
どこかで見た式・・・
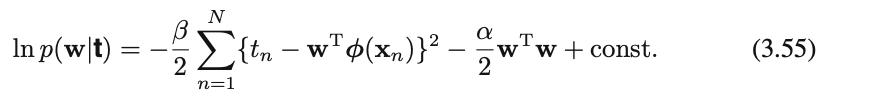
➡︎$w$に関して最⼤化することは, ⼆乗和誤差関数と⼆次の正規化項の和を最⼩化することに等しい（$λ=α/β$）
参考
https://qiita.com/kakiuchis/items/5cfe52e6f75dd75f96e7
###逐次更新の例###
単純な線形モデル$y(x,\vec{w})=w_0+w_1x$に対する逐次ベイズ学習の例
前提ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
・xは１次元の入力変数
・tは１次元の目標変数
・パラメーターαとβは既知とする（$α=2.0,β=25$）
・訓練データは$f(x,\vec{a})=a_0+a_1x$($a_0=-0.3,a_1=0.5$)にノイズを加えて生成
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
・直線を定義するには2点あれば十分なので、2点目のデータ観測ですでに不確定性の少ない事後分布が得られている
・データ観測が増えるに従って鋭い分布になっていく
##３.３.２ 予測分布##
パラーメーターを$w$を予測してたけど、
実践で本当にやりたいのは新しく観測された$x$に対する$t$を直接予測すること
➡︎(3.57)で定義される予測分布を評価する必要がある
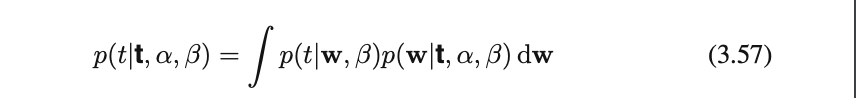
(3.8),(3.49),(2.115)から
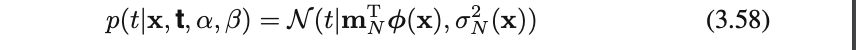
ただし
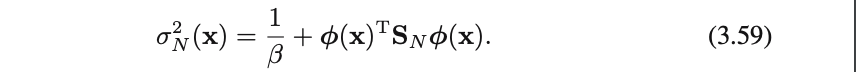
参考
P58：https://www.slideshare.net/aratahonda1/prml-3-33
Exercise 3.10：https://bicr.atr.jp//~mfukushima/PRML_resume.pdf
（3.59)はデータに含まれるノイズ＋$w$に関する不確かさ
観測データが追加されると事後分布は狭くなっていくので、$σ^2_{N+1}(x)≦σ^2_{N}(x)$が成り立ち
$N→∞$の極限では（3.59)の第二項は０に収束して、予測分布の分散はβによって決まるノイズ飲みになる
###予測分布の例###
関数$sin2πx$をガウス基底関数９個を用いたモデルで回帰
・予測の不確かさは$x$に依存し、データ点の近傍で最小となる
・観測するデータ点が増えると不確かさの度合いが減少する（標準偏差が小さくなっている）
上の事後分布から得たいくつかの$w$の標本に対する$y(x,w)のプロット$
##３.３.３ 等価カーネル##
訓練データの目標値の線形結合により予測を行う
線形基底関数モデル(3.3)に事後分布の平均解(3.53)を代入すると、予測平均を以下の形で表せる
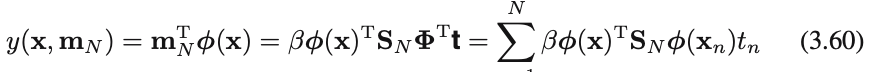
これは訓練データの⽬標変数$t_n$の線形結合になっているので
ただし
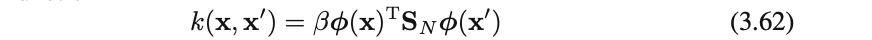
(3.62)を平滑化⾏列or等価カネールという
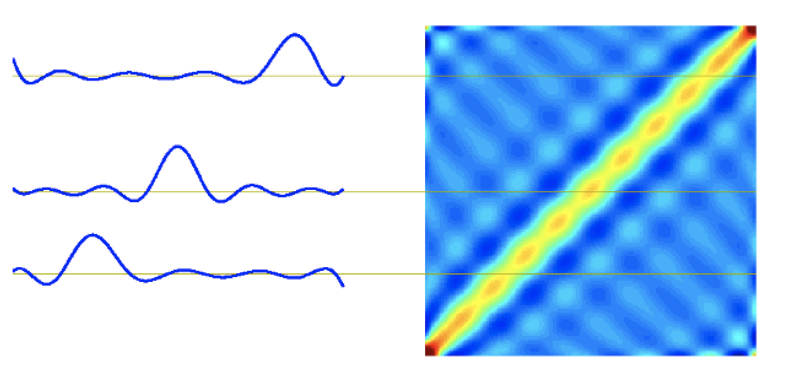
ガウス基底関数に対する等価カーネル
図3.1のガウス基底関数に対する$k(x, xʼ)$をプロット
$x$に近い$xʼ$を⼤きく重み付けしていることがわかる
多項式基底関数、シグモイド基底関数に対する等価カーネル
$x=0$の場合の$x’$をプロット
基底関数が局所的でなくても等価カーネルは$x’$に対して局所的な関数になることがわかる
その他の等価カーネル特徴（さらっと、、、）
・等価カーネルは共分散関数
P69参照：https://www.slideshare.net/aratahonda1/prml-3-33
・全てのデータ点ｘに対して、カーネル関数の合計は１
・他のカーネル関数と同様、等価カーネルは内積で表現可
##３.３.４ ベイズモデル比較##
ベイズの立場からモデル選択の問題を考えるよ
前提ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
・$M_i$はL個のモデル集合${M_i}(i=1,…,L)$
・モデルは観測されたデータ集合$D$上の確率分布
・データはL個のモデルのどれかによって生成されているが、どのモデルかは不明
・簡単のため事前確率$p(M_i)$がすべての$i$について等しい
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
訓練集合$D$が与えられたとき、モデルの事後分布は（3.66)で表せる
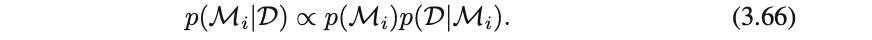
ベイズモデル比較ではモデルエビデンスと呼ばれる$p(D|M_i)$項が重要な働きをする
・モデルエビデンスはモデル$M_i$の下でのデータ$D$の起こりやすさを表している
・モデルの空間でパラメーターを周辺化した尤度関数とも見做すことができる（周辺尤度）
・モデルエビデンスの比$\frac{p(D|M_i)}{p(D|M_j)}$を**ベイズ因子（bayes factor）**という
モデルエビデンスの解釈
エビデンスの近似とか最大化する方法とかはまた後でやるっぽいので、ここではエビデンスの色々な解釈を。。。
パラメーター$w$をもつモデルに対して、モデルエビデンスは確率の加法・乗法定理より（3.68）と表せる
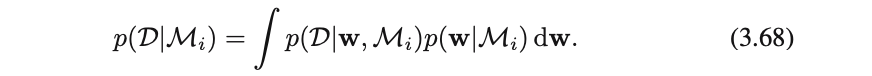
・一番もっともらしいモデル、つまりモデルエビデンスを最大化することで、モデル平均の単純な近似ができる
・サンプリング (11 章) の観点では、周辺尤度は事前分布$p(w|M_i)$からパラメータをサンプリングし、データ$D$を生成する確率と見なすことができる
・周辺尤度は事後分布を計算する際に用いるベイズの定理(3.69)の分母に表れる正規化項に等しい
また、パラメータに関する積分を単純近似することでモデルエビデンスの別の解釈を得ることができるらしいのでやってみる
まずは、簡単のためパラメータが1つしかないモデルを考える(今後Mの依存は省略)
事後分布はモデル$M_i$の依存性を省略すると$p(D|w)p(w)$に比例する
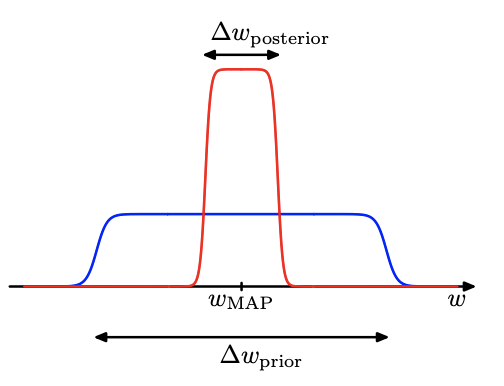
ここで事後分布が$w_{MAP}$で鋭くピークを持ち，その幅が$∆wposterior$の場合を考えると，分布の積分はピークの高さと幅の積で近似できる (図 3.12)
さらに事前分布が平坦でその幅が$∆wprior$であると仮定すれば$p(w) = \frac{1}{∆wprior}$
となるので，
さらに両辺について対数をとれば以下の式が得られる
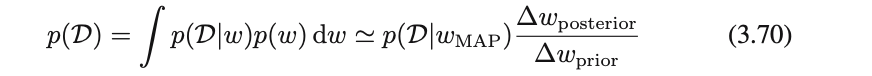
第１項はパラメータが$w_{MAP}$のときのデータへのフィティング度を表し、第２項はモデル複雑さに対するペナルティ項を表す
$∆wposterior<∆wprior$なので第２項は常に負であり、
モデルがデータに強くフィットするようにパラメータでは第２項は小さくなる＝ペナルティは大きくなる
モデルがパラメータを$M$個もつとき
同様の近似をそれぞれのパラメータについて行う
またすべてのパラメータについて $\frac{∆wposterior}{∆wprior}$ が等しいと仮定すると下記の式が得られる
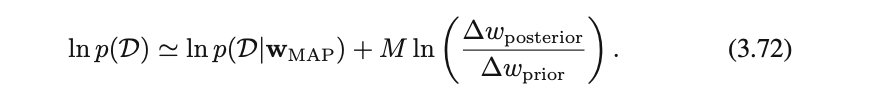
・パラメータの数が増えるとそれとともにペナルティ項も線形に増加する
・モデルを複雑にすると通常第１項は増加するが、第２項は減少する
➡︎周辺尤度最大化の観点からモデル選択を行うと、適切な複雑さを備えたモデルが選択される
図を使ってさらに検証
単純な$M_1$では$D_0$を生成出来ない
複雑な$M_3$では$D_0$になる確率が低い
ところで、、、
ベイズモデル比較は、モデル集合$M_i$の中に$D$を生成する真の分布が含まれていると仮定しているけど
その仮定って正しいの？？
モデル$M_1，M_2$を考え$M_1$が正しいモデルであると仮定して検証してみる
ベイズ因子を真のデータ生成の分布で平均すると、期待ベイズ因子が以下の形で表される
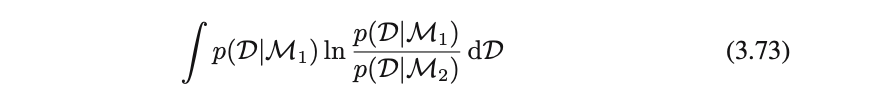
これもどこかで見た式・・・
KL-ダイバージェンスだ！
https://qiita.com/kanako-e/private/2af5ed52d7b850d36bd3#kl%E3%83%80%E3%82%A4%E3%83%90%E3%83%BC%E3%82%B8%E3%82%A7%E3%83%B3%E3%82%B9%E3%81%AE%E6%80%A7%E8%B3%AA
２つの分布が一致するときに0となり，それ以外では正となることより、
平均的には正しいモデルのベイズ因子の方が大きくなることがわかる．
まとめ
冒頭でも言ったけど、ベイズモデル比較では過学習を避けることができ、訓練データのみを用いて比較を行うことができます！
でも、、、
・他のアプローチと同様にモデルの形に関する仮定をおく必要があり、もしそれが間違っていたら誤った結果を導くことになる
・モデルエビデンスは事前分布の特性に強く依存し、変則事前分布に対しては分布が正規化できないためエビデンスを定義できない
したがって、実際の応用場面では独立なデータセットを分けておいて，そのデータを訓練終了後のシステムの評価に用いる方がよい（結局使えないってこと・・・？）