はじめに
「これからの強化学習」読んでますか?>挨拶
「これからの強化学習」の1.2節には、三目並べが出てきます。多椀バンディット問題と異なり、エージェントの行動が環境を変えます。また、報酬を「勝ったら+1、負けたら-1」とすると、決着するまで報酬が決まりません。そんな条件でどうやって指し手を考えればいいだろう、というのが主題です(多分)。
さて、AIの思考ルーチンを作るのに、例えばモンテカルロ木探索とかするわけですが、こういう(疑似)乱数が入ったコードのデバッグというのは一般に極めて困難です。そこで、厳密解がわかる小さな系で比較したくなるわけですね。
三目並べの手数ですが、9マスに交互に石を置いていくため、石をすべて区別したとしても9! = 362880通り、つまり対称性などを考えなくても楽勝で全探索ができます1。なので、ここでは全探索して、「もしすべての手を完全に読める神がいたら、評価関数はどうなるか」を計算してみようと思います。
コードはここに置いてあります。
使い方
内容を説明する前に、簡単な使い方の説明です。スクリプトには「状態」「確率を表示するか」「ファイル名」を指定できます。
マスの状態は、9文字の文字列で指定します。それぞれ「空白:0、先手:1、後手:2」です。
ただ状態を指定するとそのまま表示します。
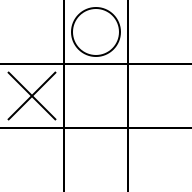
$ ruby ttt.rb 010200000
Input state
|o|
x| |
| |
-o FILENAMEで、状態をファイルに出力します。
$ ruby ttt.rb 010200000 -o fig1.png
Input state
|o|
x| |
| |
Save to fig1.png
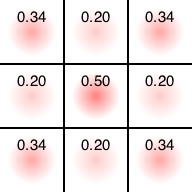
-sオプションをつけると確率を出力します。
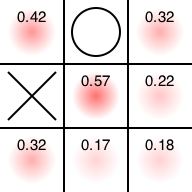
$ ruby ttt.rb 010200000 -s
Input state
|o|
x| |
| |
Probability
+0.42|+0.00|+0.32
+0.00|+0.57|+0.22
+0.32|+0.17|+0.18
これは現在の盤面の評価値で「この状態でどこに置いたらどれだけ有利になるか」を表す数値です。数字が大きいほど先手有利、小さいほど後手有利となります。
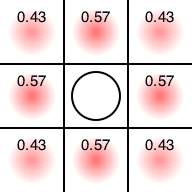
同時にファイル出力すると、画像ファイルに確率情報が出力されます。
$ ruby ttt.rb 010200000 -s -o fig2.png
Input state
|o|
x| |
| |
Probability
+0.42|+0.00|+0.32
+0.00|+0.57|+0.22
+0.32|+0.17|+0.18
Save to fig2.png
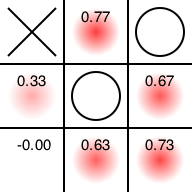
先手有利の思われるところ(そこに打つと勝率が高い)が赤く表示されています。
逆に、そこに置いたら不利になる場所は青く表示されます。
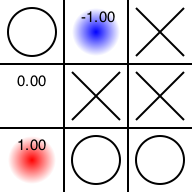
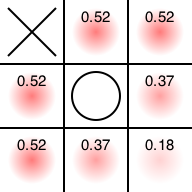
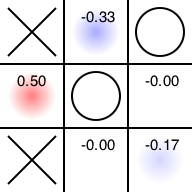
$ ruby ttt.rb 102022011 -s -o fig3.png
Input state
o| |x
|x|x
|o|o
Probability
+0.00|-1.00|+0.00
+0.00|+0.00|+0.00
+1.00|+0.00|+0.00
Save to fig3.png
後は戯言のようなものです。
評価関数とは何か
将棋や囲碁のように、交互に何かをするゲームでは、「相手の思考を読む」必要があります。人間は「この人は棒銀が好きだからこうやって受けよう」とか、「この人は乱戦になると脆いからそこに勝機を見出そう」とか考えるわけですが、一般論としてAIは、「相手は自分と同じように考える」と仮定して読みを進めます2。
さて、三目並べの「評価関数」とか何かを考えましょう。非常に簡単に言えば、「現在の状態が与えられた時、どこに打てばどれだけ勝つ確率があるか」で定義したくなります。
しかし、よく知られているように、三目並べはお互いが最善手を打つと必ず引き分けになります。そういう意味において、もし「相手が最善手を打つ」と仮定して確率を計算してしまうと、最初の何も置いていない場面は評価値オールゼロ、後は勝負が決まる盤面でその手筋のみ「1 (勝利)」、そうでないところは「0 (引き分け)」か「負け (-1)」という状態になってしまいます。
三目並べは「解かれている」問題なのでそれで良いのですが、いくら全探索可能とはいえ、それでは面白くありません。
そこで、「自分も相手も完全にランダムにプレイする」と仮定して、その状態で全探索することにしましょう。
こうすると、例えば相手が「勝ち確定」の手があるときにもその手を差さないという状況になってしまいますが、かまわず全探索してしまいます。
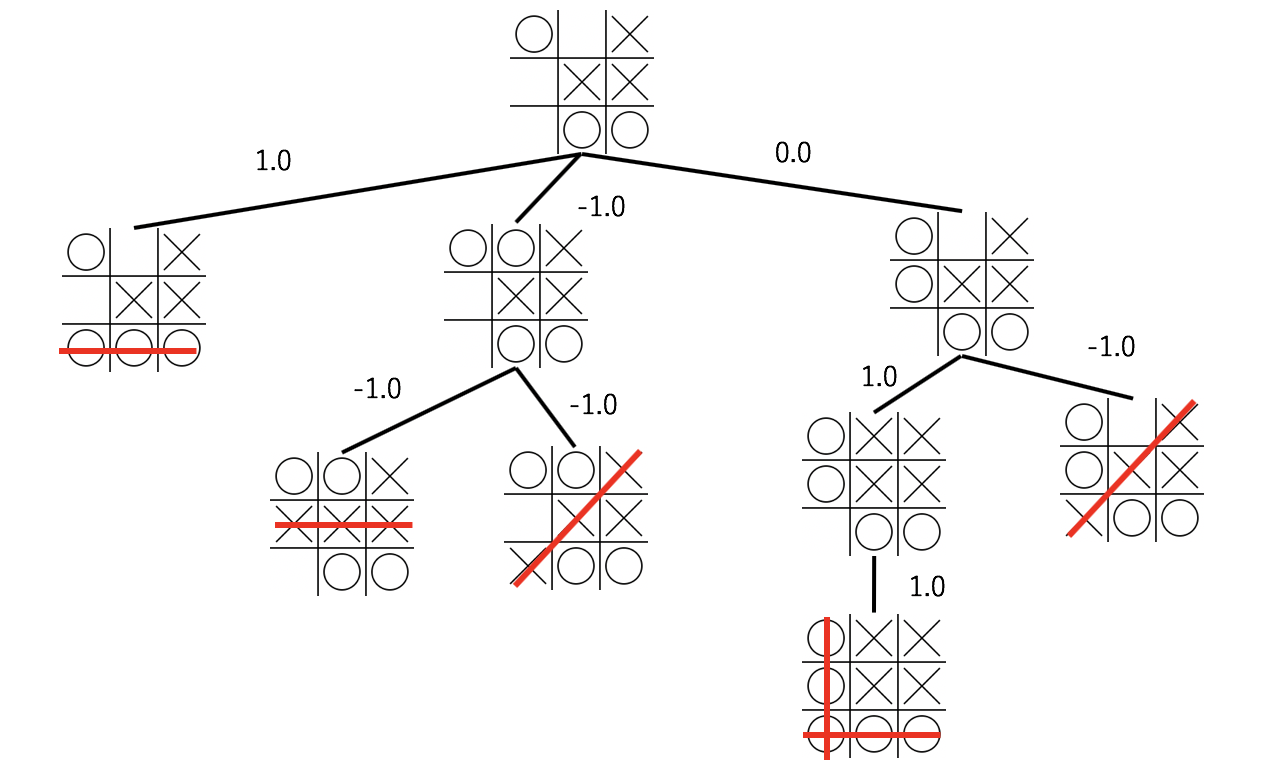
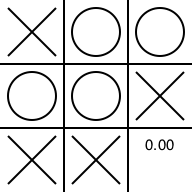
例えばこんな状態を考えましょう(実戦でこんな場面でてこないと思いますが)3。
次は先手番ですので勝ち確定ですが、あえて別の場所に打ったらどうなるか考えてみます。ここからの探索木はこんな感じです。
勝負が確定するまで木を展開し、勝ちなら+1、負けなら-1、引き分けなら0として、子ノードの平均を自分の手の評価値と考えることにします。
一番左にいけば勝ち確定なので1、真ん中の枝は負け確定なので-1、右の道は勝ちの未来と負けの未来があるのでちょうど0、といった具合です。
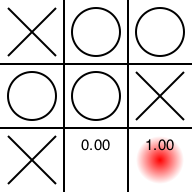
この確率を表示したものがこちらの図です。
赤(1.0)のマスに打ったら勝ち確定、青(-1.0)のマスに打ったら負け確定、0.0のマスに打ったらわからない、という意味です。これは評価値0のマスに打ったあと、後手が「勝利手があるにもかかわらずそれを見逃す」という行動を期待していることになりますので、これはおかしな仮定です。ですが、「後手が最善手を打つ」と仮定してしまうと完全引き分けとなり、評価関数が1か0か-1のみになって面白くないので、とりあえずこれで良しとします。
対戦してみる
さて、「自分も相手も全くランダムに打つ」と仮定して得られた「勝利確率」を「その盤面における行動価値関数」だと思って、その思考ルーチンが強いのか弱いのか調べてみましょう。「CPU」を先手番にします。
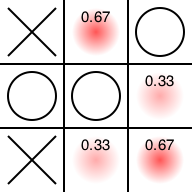
まず初期状態はこうなっています。
真ん中に置きたがってますね。そこに置いてあげましょう。
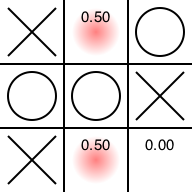
さて、いまは後手番なので、「後手番がそこに置いてくれたら勝つ確率が高くなる」場所の数値が高くなっています。端において欲しくなさそうですね。そこに置いてみましょう。
まだ先手有利は揺らぎません。置きたがってるマスが4つほどあります。適当に選んでみます。
後手番となりました。「後手がそこに置かないと先手の勝ちが確定する場所」を(当たり前ですが)もっとも嫌がっています。当然そこに置きます。
先手番です。「そこにおかないと後手番の勝ちが確定する」場所に置きたがっています。置かせてあげましょう。
後手番です。先手の勝ち目があるのでつぶします。
先手番です。まだ勝つ可能性が残る場所に置きたがっています。置かせてあげましょう。
後手番です。「後手がそこに置いてくれたら勝てるなぁ」という場所が赤く光っています。もちろんそこには置けません。
引き分けが確定しました。
まとめ
というわけで、「自分も相手も全くランダムに打つ」と仮定して全探索して計算した「勝利確率」を「行動価値関数」だと思ってAIの思考ルーチンを作ってもまぁまぁいけそうだ、ということがわかりました。これは要するに「ランダムなプレイアウトを十分な回数行った」結果です。ここから逆に「たとえ思考ルーチンがランダムであったとしても、十分な回数のプレイアウト(モンテカルロサンプリング)を行えばそこそこ強くなれそう」ということがわかりますね。
あとすごくどうでもいいですが、三目並べって、日本だと先手が「○」ですが、海外だと先手が「☓」が多いみたいですね。さらにどうでもいいことですが、Googleで「三目並べ」や「Tic Tac Toe」で検索すると三目並べができます。激しく接待プレイですが、もしまだやったことがない方はどうぞ4。
参考
他に三目並べの強化学習を行っている記事は多数あるため、参考のためにリンクをはっておきます。
- ChainerRLで三目並べを深層強化学習(Double DQN)してみた
- 三目並べをAlphaZeroで学習させる
- 三目並べを強化学習する
- Pylearn2で三目並べのAIをつくってみる
- モンテカルロ木構造(Monte Carlo Tree Search) MCTS その3
-
ちなみに実際の状態数はもっと少ないようです。詳細はWikipediaのTic-tac-toeの項目を参照。 ↩
-
昔はプロとの戦いの前などでいろいろ調整をしていたと思いますが、最近はそういう調整はしてないんじゃないかと思います。考え違いだったらすみません。 ↩
-
っていうかもう三目並べなんてやらないと思いますが・・・ ↩
-
いや、僕が実装したわけじゃないですけど。 ↩