はじめに
これからの強化学習という本があり、強化学習の新しい教科書として広く読まれはじめているようです。ですが、概念を数式できちんと定義していくスタイルで、かつ擬似コードやサンプルコードがほぼ無いというかなりソリッドな本で、これを読んで何かを実装するまで持っていくのは結構きついです。
ただ、1.1節に出てくる多椀バンディット問題についてはネットにわりとサンプル実装が転がっています。しかし、そのほとんどはPythonです。機械学習っていうと猫も杓子もPythonですね。それはそれでいいのですが、せっかくRubyで書いたのでそのコードを晒します。
コードはここに置いてあります。
多椀バンディット問題とは
多椀バンディット問題(Multi-Armed Bandit problem)とは、カジノに複数のスロットマシンがあるときに、もっとも儲かるような戦略を考える問題です。ただし、スロットマシンは当たる確率と、当たった時の報酬が固定されています。従って、最も報酬の期待値が高いスロットマシンをどうやって推定するか、という問題になっています1。
多椀バンディット問題は、強化学習の問題として考えると、
- 報酬が即時報酬しかない (遅延報酬がないため、「損して得取れ」のような戦略がない)
- 行動の結果、条件が変わらない (将棋のように、行動の結果として環境が変わらない)
という特徴があるため、問題がかなり簡略化されます。
というわけでこの問題をスクリプトを組みながら考えてみましょう。以下、スロットマシンを「腕」と呼びます。
カジノとプレイヤークラスの実装
まずはスロットマシンを束ねるカジノクラスを作るんですかね。
スロットマシンは「当たる確率」「当たった場合の報酬」の組で定義され、さらにそれがいくつか集まったものがカジノですから、こんな感じに定義したいところです。
bs = [[0.2, 1], [0.3, 1], [0.4, 1], [0.5, 1]]
c = Casino.new(bs)
そして、プレイする腕のインデックスを選ぶと、その腕の報酬を確率的に返してほしいところです。
以上を考えるとこんな実装になるでしょうか。
# 複数のバンディットをまとめるクラス
class Casino
Bandit = Struct.new(:prob, :award)
def initialize(arr)
@bandits = []
arr.each do |prob, award|
@bandits << Bandit.new(prob, award)
end
end
# プレイする腕を選ぶと、その腕の確率でawardを返す
def play(index)
if @bandits[index].prob > rand
@bandits[index].award
else
0
end
end
end
簡単ですね。
プレイヤーは、毎回「腕」を選ぶ必要があるので、最低限知って置かなければいけないのは「何本の腕があるか」です。また、後で「これまでの平均報酬」も知りたくなるでしょうから、それだけ定義しておきましょう。
# プレイヤークラス
class Player
def initialize(num:)
@num_bandits = num
@awards = 0.0
@t = 0
end
def average_awards
@awards.to_f / @t
end
end
以下、このPlayerクラスを継承し、playを定義していくことでプレイヤーを作ります。
ランダムプレイヤー
一番簡単なのは、「何も考えずにランダムに選ぶ」プレイヤーですね。
# ランダム
class RandomPlayer < Player
def play(casino)
@t += 1
i = rand(@num_bandits)
@awards += casino.play(i)
end
end
playにカジノクラスのインスタンスが渡されるので、そこに腕のインデックスをランダムに放り込むだけです。報酬が返ってくるので、それを総報酬@awardsに足しこんでいます。
Greedy
次に簡単なアルゴリズムは、「最初に最低n回ずつお試し」して、あとは「これまでに最も報酬期待値が良かったものを選ぶ」というアルゴリズムです。Greedyアルゴリズムと呼ばれます。
アルゴリズムとしては
- まだn回選んでない腕があったらそれを選ぶ
- すべてn回以上選んでいたら、報酬の期待値もっとも高い腕を選ぶ
となります。実装はこんな感じになるでしょうか。
# Greedy Player
class GreedyPlayer < Player
# min: 最低何回試すか
def initialize(num:, min:)
super(num: num)
@num_trials = Array.new(num) { 0 }
@got_awards = Array.new(num) { 0 }
@min_trials = min
end
def play(casino)
@t += 1
# まだ規定回数試していない腕があるか調べる
i = @num_trials.find_index { |v| v < @min_trials }
if i.nil? # すべて規定回数試した
i = @got_awards.index(@got_awards.max)
@awards += casino.play(i)
else # 規定回数試していない腕がある
a = casino.play(i)
@got_awards[i] += a
@awards += a
@num_trials[i] += 1
end
end
end
Greedyアルゴリズムの問題点として挙げられるのが「楽観的な誤りは正せるが、悲観的な誤りは正せない」というものです。
簡単のため、「お試し」を1度にしてしまいましょう。確率0.1で200の報酬が得られる腕Aと、確率1で100の報酬が得られる腕Bがあるとします。しかし、運良くこの人はAであたりを引いてしまいました。この人は一度ずつプレイした結果として
- Aの期待値: 200
- Bの期待値: 100
となっており、Aをプレイし続けます。ところが、実際にはAの報酬の期待値は20であり、遊んでいるうちにだんだん期待値が減ってきて、「あ、やっぱりBの方がいいじゃん」と、行動を修正します。
逆に、確率0.1で10000の報酬が得られる腕Aと、確率1で100の報酬が得られる腕Bがあったとしましょう。この人は一度ずつ遊んでみて、Aは外れてしまったので
- Aの期待値: 0
- Bの期待値: 100
だと思っており、今後はBだけを遊び続けます。Aの方が期待値(1000)が高いのに、Aはプレイされないためにその認識が改められることはありません。
教科書では
不確かな時は楽観的に(optimism in face of uncertainity)
と格言的に紹介されています。
ε-Greedy
Greedy法は最適戦略を見つけられない可能性がありました。そこで、小さい確率で行動にノイズを入れます。具体的には
- 一度も選んでない腕があればそれを選ぶ
- すべての腕を遊んだことがあれば
- 確率1-εで報酬期待値が最も高いものを選ぶ
- 確率εでランダムに選ぶ
簡単に言えば、ランダム戦略とGreedy戦略のハイブリッド戦略です。この「行動にランダムノイズを載せる」というのは単純ですがわりと強力な戦略で、様々な分野で効果を挙げています2。
実装はこんな感じでしょうか。
# epsilon-Greedy
class EGreedyPlayer < Player
# n: banditの数
# e: 確率epsilon
def initialize(num:, eps:)
super({num: num})
@num_trials = Array.new(num) { 0 }
@got_awards = Array.new(num) { 0 }
@epsilon = eps
end
def select_epsilon
if rand < @epsilon # 確率epsilonでランダム
rand(@num_bandits)
else
r = Array.new(@num_bandits) { |j| @got_awards[j].to_f / @num_trials[j] }
r.index(r.max)
end
end
def play(casino)
@t += 1
# まで試してない腕があったらそれを選ぶ
i = @num_trials.find_index(&:zero?)
i = select_epsilon if i.nil?
a = casino.play(i)
@num_trials[i] += 1
@got_awards[i] += a
@awards += a
end
end
ε-Greedyの弱点としては、「多数の試行により十分な知見が得られたにもかかわらず、一定確率でランダムに選ぶので、その分報酬の期待値が下がってしまう」というものが挙げられます。そのため、徐々にεを下げていく、などの改良が考えられます(いわゆるアニーリング)。
UCB1
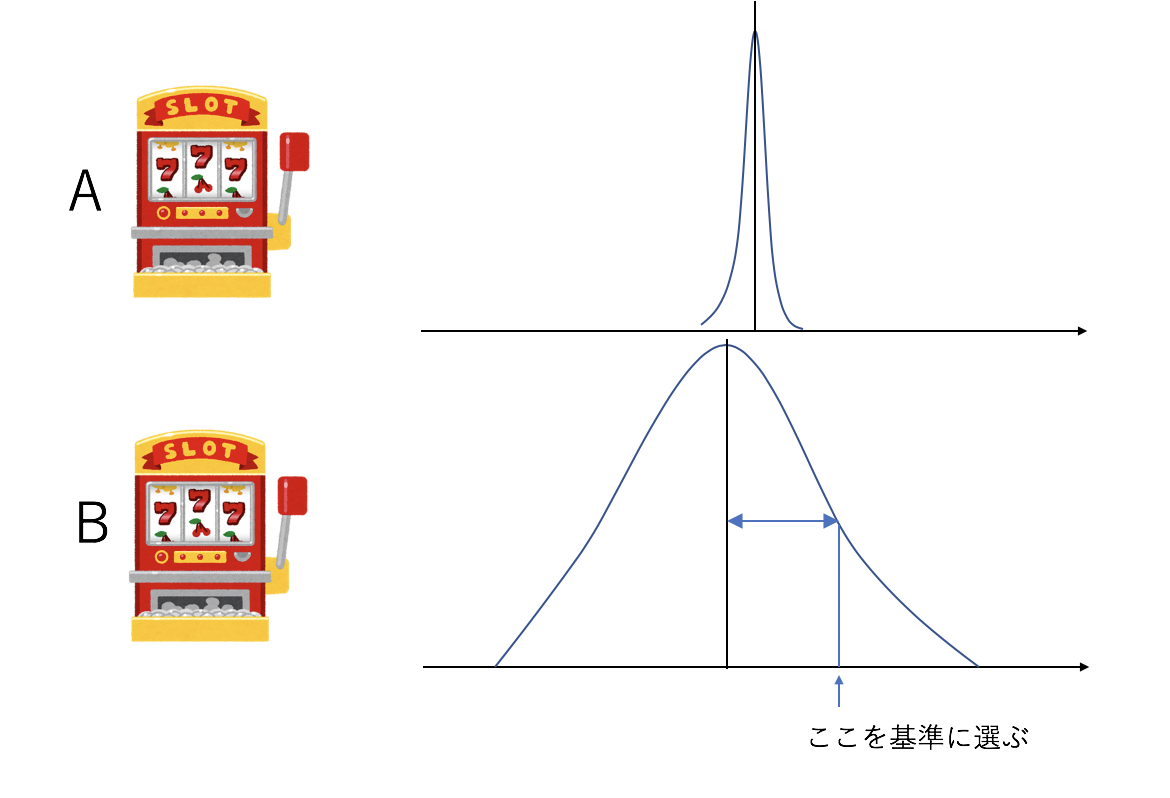
さて、「これからの強化学習」1.1節のハイライトはUCB1です。UCBはUpper Confident Boundの略で
簡単に言えば
- これまでの報酬期待値と、期待値の不確かさの半値幅の和が最大のものを選ぶ
というアルゴリズムです。
例えば「たくさん遊んだ腕Aと、ほとんど遊んでない腕Bがあり、腕Aの方が報酬の期待値が大きいことがわかっているが、Bについてはまだ十分な知見が得られていない」という状況で、単純なGreedyではAを選びますが、UCB1ではBを選びます。
そしてBに対する知見が集まって、「本当にAの方が良い」という自信がついたらAを選ぶことになります。
これまでの総プレイ回数を$t$、腕$i$のプレイ回数を$t_i$として、腕$i$の信頼区間の半値幅$U_i$は
U_i = \sqrt{\frac{2 \ln t}{t_i}}
で計算されます。UCB1はこれまでの腕$i$の報酬期待値を$\mu_i$として、$\mu_i + U_i$が最大になるような$i$を選ぶ戦略です。
実装はこんな感じになるでしょう。
# UCB1戦略
class UCB1Player < Player
# n: banditの数
# e: 確率epsilon
def initialize(num:)
super({num: num})
@num_trials = Array.new(num) { 0.0 }
@got_awards = Array.new(num) { 0.0 }
@max = 0.0
end
def select_ucb
mu = @got_awards.zip(@num_trials).map { |x, y| x / y }
r = Array.new(@num_bandits) do |j|
# 半値幅
u = Math.sqrt(2.0 * Math.log(@t) / @num_trials[j])
# 期待値と半値幅の和を返す
mu[j] + u
end
r.index(r.max)
end
def play(casino)
@t += 1
# まで試してない腕があったらそれを選ぶ
i = @num_trials.find_index(&:zero?)
# 全て試していたら半値幅と平均の和が最大の腕を選ぶ
i = select_ucb if i.nil?
a = casino.play(i)
@num_trials[i] += 1
@got_awards[i] += a
@awards += a
@max = a if @max < a
end
end
結果
というわけで教科書どおり、報酬を1に固定し、当選確率が0.2, 0.3, 0.4, 0.5の4つの腕があるカジノで、上記のプレイヤーを遊ばせてみましょう。
テストコードはこんな感じになるでしょうか。
N = 100
T = 10000
def test(pclass, args, casino)
ninv = 1.0 / N
r = Array.new(T) { 0.0 }
N.times do
player = pclass.new(args)
T.times do |i|
player.play(casino)
r[i] += player.average_awards * ninv
end
end
r
end
bs = [[0.2, 1], [0.3, 1], [0.4, 1], [0.5, 1]]
c = Casino.new(bs)
rp = test(RandomPlayer, {num: bs.size}, c)
gp = test(GreedyPlayer, {num: bs.size, min: 10}, c)
egp = test(EGreedyPlayer, {num: bs.size, eps: 0.1}, c)
up = test(UCB1Player, {num: bs.size}, c)
T.times do |t|
puts "#{t} #{rp[t]} #{gp[t]} #{egp[t]} #{up[t]}" if (t % 100).zero?
end
パラメータは
- Greedyの最低試行回数は10 3
- ε-Greedyのεは0.1
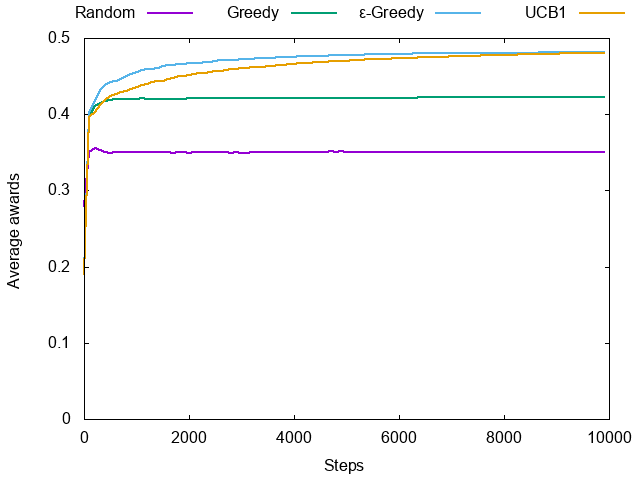
としています。教科書では10000ステップを10000回試してますが、遅かったので100回しか平均していません。結果はこんな感じです。
UCB1は最終的には最適戦略に収束するので、必ずε-Greedyに勝つはずですが、収束が遅いので、この時間内ではまだ勝ててないですね。
まとめ
「これからの強化学習」の1.1節に紹介されている多椀バンディット問題を問いてみました。この問題の解説は多数ありますが、西尾さんによる以下のスライドが特に教育的だと思います。
すごくどうでもいいんですけど、今回からRubocop入れてみたんですが、この人厳しすぎません?特にABCメトリクス超過警告を消すのにすげー時間がかかりました。慣れれば最初からひっかからないコードが書けるのかもしれませんが・・・4