ABC409に参加しました。
今回はD問題が茶色上位、E問題が緑色中位となっており、緑色コーダーの自分にとっては程よい難易度での5完となりました。
そろそろレート4桁が見えてきたかな...
A : Conflict
高橋君と青木君がどちらも欲しい商品があるかを確認していきましょう。
#include <bits/stdc++.h>
using namespace std;
#define rep(i,n) for(long long i=0;i<n;i++)
using ll = long long;
using Graph = vector<vector<int>>;
int main() {
int n;
cin >> n;
string a, b;
cin >> a >> b;
rep(i,n){
// 両方oならYesを出力してreturn
if(a[i] == 'o' && a[i] == b[i]){
cout << "Yes";
return 0;
}
}
// 条件を満たす商品が存在しなければNo
cout << "No";
return 0;
}
B : Citation
配列を用意して入力された値の要素を+1したあとで累積和を取ると解けそうな気がしますが、入力の最大値が$10^9$なので厳しいです。
しかしよく見ると$N ≤ 100$であることから要素数の最大は$100$なので、$x≤100$となることがわかります。
ということで$x$について全探索することでこの問題を解くことができます。
#include <bits/stdc++.h>
using namespace std;
#define rep(i,n) for(long long i=0;i<n;i++)
using ll = long long;
using Graph = vector<vector<int>>;
int main() {
int n;
cin >> n;
vector<int> a(n);
rep(i,n)cin >> a[i];
int ans = 0;
rep(i,101){
int cnt = 0;
rep(j,n){
if(a[j] >= i)cnt++;
}
// cnt(i以上の要素数)がiより大きければansを更新
if(cnt >= i)ans = i;
}
cout << ans;
return 0;
}
C : Equilateral Triangle
数学の問題ですね。
正$N$角形の頂点を結んで正三角形を何種類作れるかと考えることができます。
正三角形を作るためには円を三等分した点を取る必要があるので、$N$が3の倍数でない場合には答えは0となります。
$N$が3の倍数の時は正三角形を作ることができます。この時、点$a,b,c$間の距離はそれぞれ$l/3$であり、$a<b<c$であることに注意すると、点$a$を$0$ ~ $l/3$の範囲で動かせば全てのパターンを調べることができます。
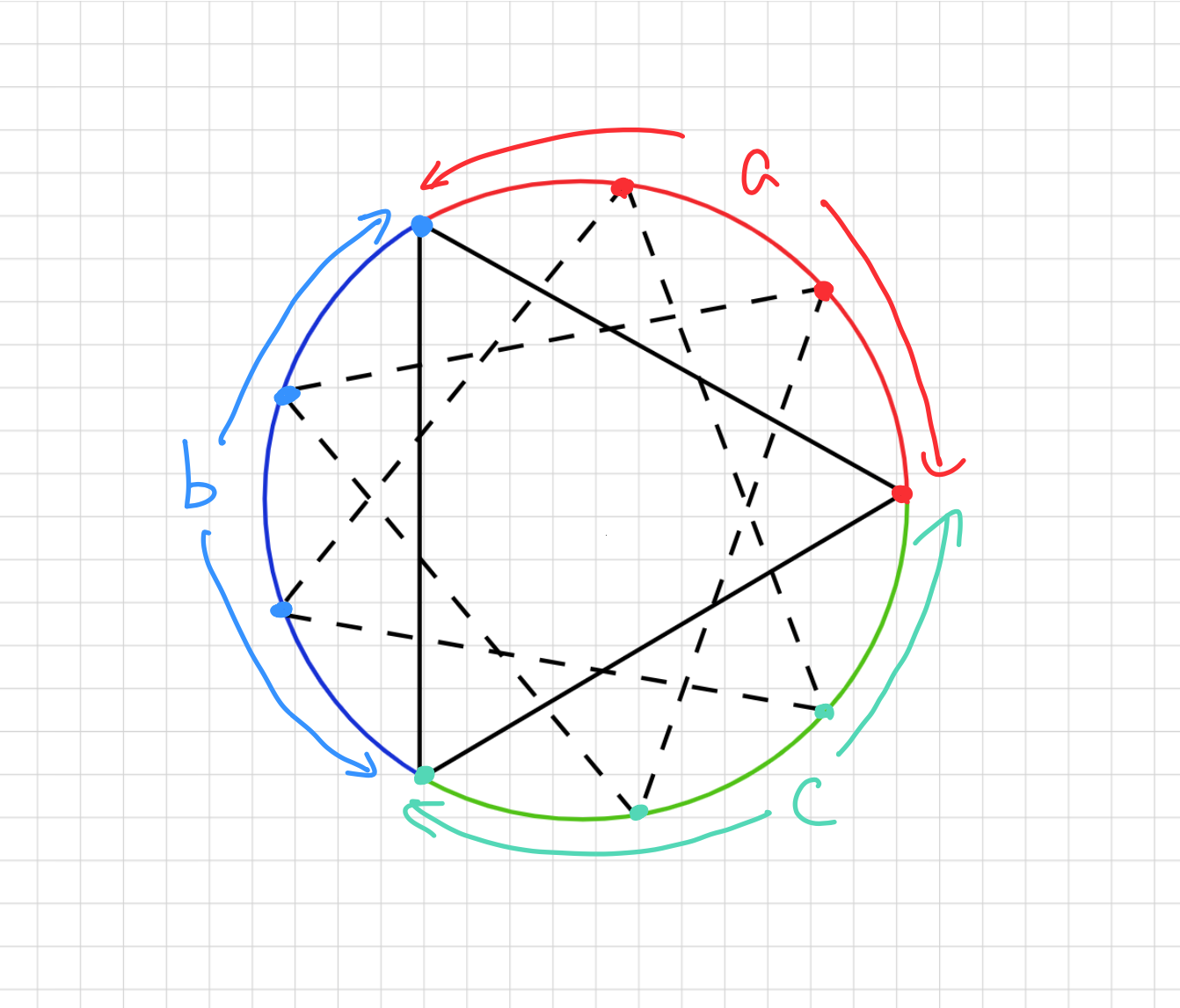
入力される点は前の点との距離のみが渡されるので受け取り方も工夫しないといけません。今回の実装では最初に距離$0$に点を置いておき、受け取った距離を足した位置に新しい点を置いています。
#include <bits/stdc++.h>
using namespace std;
#define rep(i,n) for(long long i=0;i<n;i++)
using ll = long long;
using Graph = vector<vector<int>>;
int main() {
ll n,l;
cin >> n >> l;
if(l % 3 != 0){
cout << "0";
return 0;
}
vector<ll> a(l,0);
a[0] = 1; // 最初の点はl=0の位置にあるとする
ll now = 0; // 現在の点の位置
// 円をn分割したそれぞれに何個頂点があるのかを記録していく
rep(i,n-1){
int tmp;
cin >> tmp;
now += tmp; // 距離を足すことで新しい頂点の位置を確定
now %= l; // 範囲は0~l-1なのでlで割ったあまりを取る
a[now]++;
}
ll t = l/3;
ll ans = 0;
// 答えは正三角形の頂点となる点の積で求められる
rep(i,t){
ans += a[i]*a[i+t]*a[i+2*t];
}
cout << ans;
return 0;
}
D : String Rotation
なかなか問題の読解が難しいです。
一言でいうと
- 文字列から一文字を抜き出して後ろのどこかに挿入することでできる文字列で辞書順最小のものを求めよ
となります。
まず考えたいのは文字を移動させることで辞書順はどう変化するのかです。
例えば$atcoder$という文字列に対して$a$を選んで後ろに移動させた場合、$a$をどこに移動したとしても先頭の文字は$t$になります。つまり$i$文字目を選ぶと元々の$i+1$文字目が新たに$i$文字目になります。
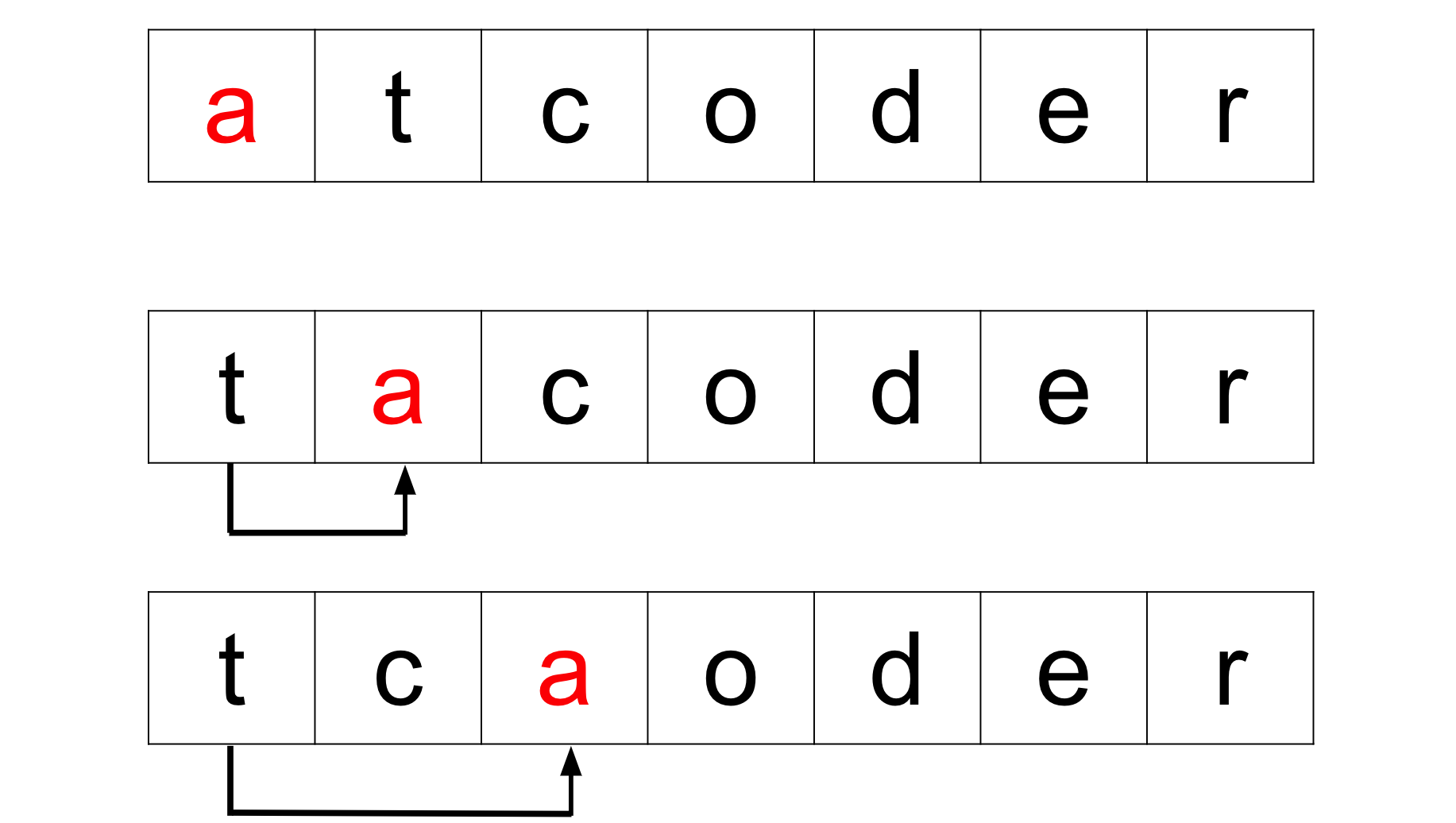
ここからわかることとしては$i$文字目と$i+1$文字目を見た時に$i$文字目より$i+i$文字目の方が辞書順で小さい時、$i$文字目を移動することで文字列の辞書順を小さくできるということです。($i$文字目のことを以降転倒文字と呼びます)
また文字列の先頭に近い部分の方が辞書順に影響を与えるので、選ぶべき文字は文字列を前から見ていったときに最初の転倒文字となります。
次に考えるのは選んだ文字をどこまで移動させるかです。
これは選んだ文字を移動した後の状態でも転倒文字であるならば、さらに移動することで辞書順を小さくできるので、選んだ文字が転倒文字でなくなるまで移動するのが最適であることがわかります。
ちなみに移動中に現在の文字と次の文字が一致している場合はさらに移動することが最適になります。(1敗)
#include <bits/stdc++.h>
using namespace std;
#define rep(i,n) for(long long i=0;i<n;i++)
using ll = long long;
using Graph = vector<vector<int>>;
void solve(){
int n;
string s;
cin >> n >> s;
int tmp = 0;
while(tmp < n && s[tmp] <= s[tmp+1])tmp++;
if(tmp == n){
cout << s << endl;
return;
}
int t = tmp;
while(tmp < n && s[t] >= s[tmp+1])tmp++;
if(tmp == n){
rep(i,n)if(i != t)cout << s[i];
cout << s[t] << endl;
}else{
rep(i,n){
if(i != t)cout << s[i];
if(i == tmp)cout << s[t];
}
cout << endl;
}
}
int main() {
int n;
cin >> n;
rep(i,n)solve();
return 0;
}
E : Pair Annihilation
実験をしてみると木の葉から根に集めていくように電子を移動させることが最適だとわかります。(未証明)
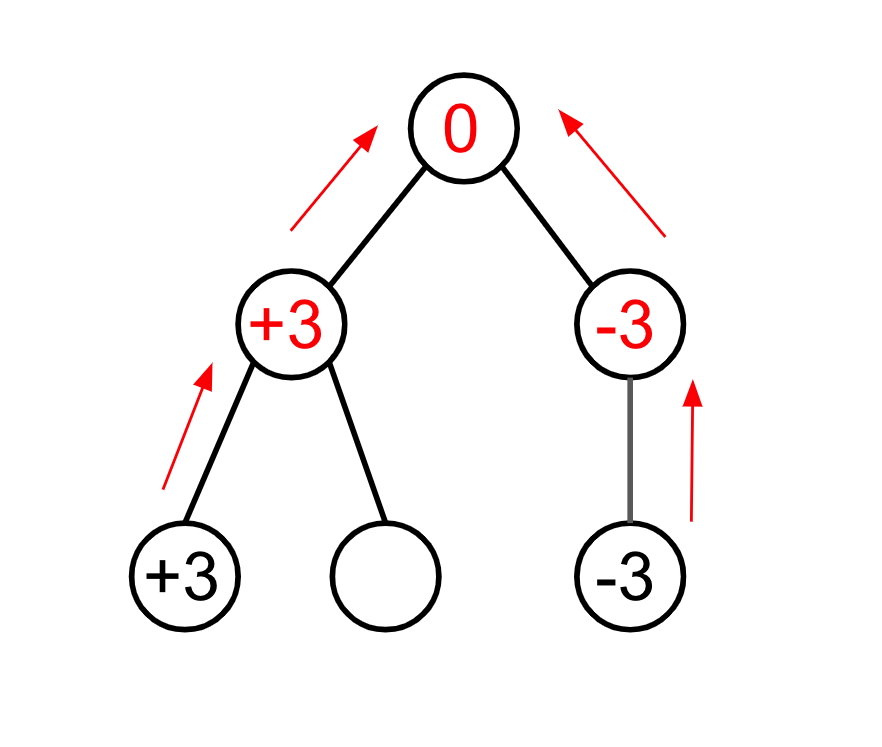
(ペアとなるべき電子はそれらが重なるノードまで移動しないと消滅しない)
したがって実装方針としては深さ優先探索をしながら帰りがけに電子を集めていく方法とします。
#include <bits/stdc++.h>
using namespace std;
#define rep(i,n) for(long long i=0;i<n;i++)
using ll = long long;
using Graph = vector<vector<pair<ll,ll>>>;
vector<ll> e,visited; // e : 各頂点の電荷の数
Graph g;
ll ans = 0;
ll dfs(ll now){
for(auto [t,u] : g[now]){
if(visited[t])continue;
visited[t] = true;
// 子ノードから受け取った電荷を加算する
e[now] += dfs(t);
// 動かす電荷の絶対値分エネルギーを加算する
ans += abs(e[t]*u);
}
return e[now];
}
int main() {
ll n;
cin >> n;
e.resize(n);
g.resize(n);
visited.resize(n,false);
rep(i,n){
ll t;
cin >> t;
e[i] = t;
}
rep(i,n-1){
ll a, b, c;
cin >> a >> b >> c;
a--;
b--;
g[a].push_back({b,c});
g[b].push_back({a,c});
}
visited[0] = true;
dfs(0);
cout << ans;
return 0;
}
F : Connecting Points
この問題も問題文がなかなか難しいですがゆっくり解読していきましょう。
$G$の頂点$u,v$に対して、$u,v$の距離$d$をマンハッタン距離$d(u,v) = |x_u - x_v|+|y_u - y_v|$で定義します。
これは頂点どうしの距離を($x$座標の距離)$+$($y$座標の距離)とするということですね。
$G$の二つの連結成分$A,B$に対して、$A,B$の頂点集合をそれぞれ$V(A),V(B)$としたとき、$A,B$の距離$d(A,B)$を$d(A,B) = min \{ d(u,v) | u∈V(A),v∈V(B)\}$で定義します。
頂点をいくつか連結したものに対しての距離の定義ですね。
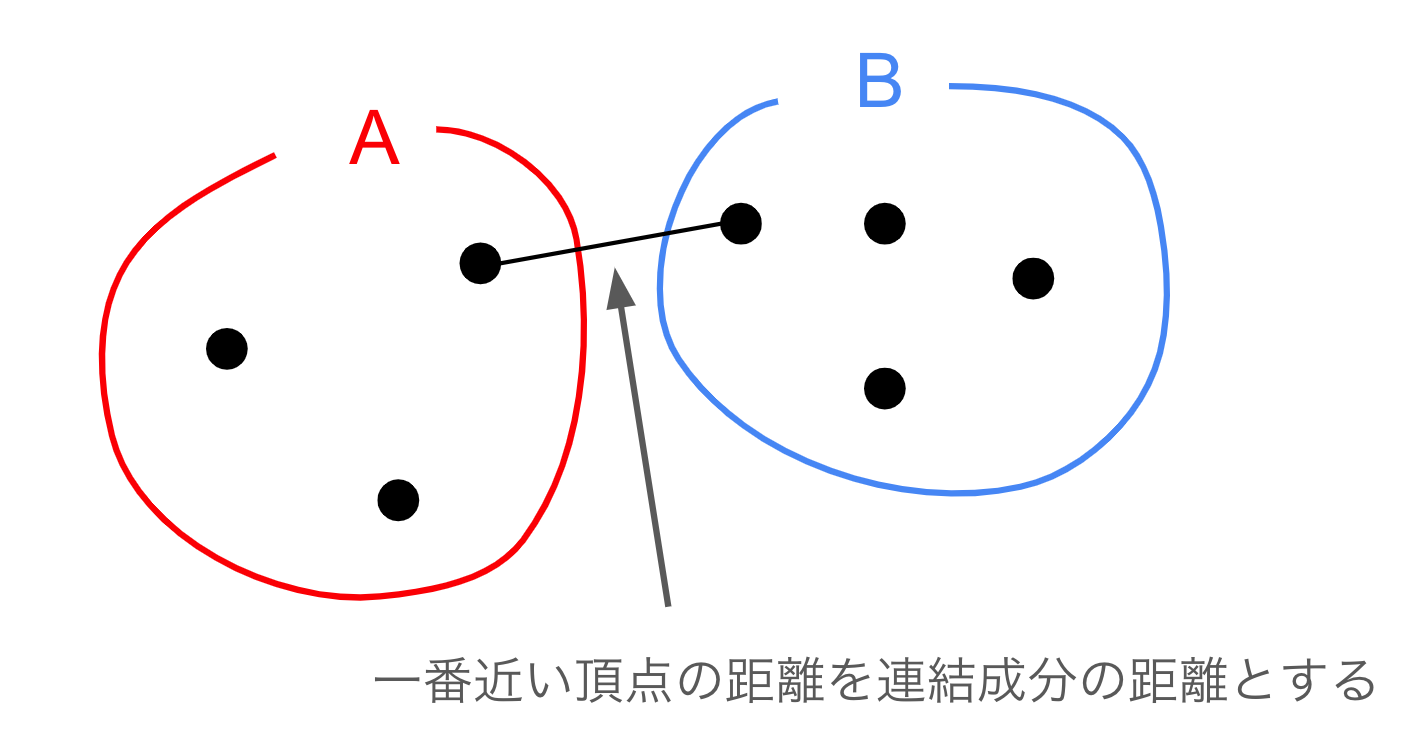
一言でいうと、
- 連結成分どうしの距離は、連結成分間で一番近い頂点の距離とする
それぞれのクエリは
- クエリ1 : 頂点を追加する
- クエリ2 : 距離が最短である全ての頂点を結ぶ
- クエリ3 : 二つの頂点が繋がっているか判定
となっています。
クエリ3はUnion-Findでできそうですね。
クエリ1もいけそうです。
問題はクエリ2です。愚直に考えると、全ての頂点どうしの距離を計算して最短距離を特定する方法が考えられます。頂点のペアは$_NC_2 = N(N-1)/2$種類、クエリが$Q$個なので計算量は$Θ(N^2Q)$となります。これは$N≤ 1500, Q≤ 1500$よりTLEしてしまいます。
この問題を解決するために優先度付きキューを使います。全ての距離を前計算して優先度付きキューに入れておくことで最短距離のペアを高速で見つけられるようになります。
キューに追加する頂点ペアの数は$_{N+Q}C_2 = (N+Q)(N + Q-1)/2$種類、追加に$Θ(log(N+Q))$かかるので、全体で$Θ((N+Q)^2log(N+Q))$でこの問題が解けました。
#include <bits/stdc++.h>
using namespace std;
#define rep(i,n) for(long long i=0;i<n;i++)
using ll = long long;
using Graph = vector<vector<int>>;
using Pair = pair<ll, ll>;
using Tuple = tuple<ll, ll, ll>;
struct UnionFind{
vector<int> par, rank, size, edge_count;
int cnt; // 繋いだ辺の数
UnionFind(int N) : par(N), rank(N, 0){
for(int i = 0; i < N; i++)par[i] = i;
cnt = 0;
}
int root(int x){
if(par[x] == x)return x;
return par[x] = root(par[x]);
}
void unite(int x, int y){
int rx = root(x);
int ry = root(y);
if(rx == ry){
edge_count[rx]++;
return;
}
cnt++;
if(rank[rx] > rank[ry])swap(rx, ry);
par[rx] = ry;
if(rank[rx] == rank[ry])rank[ry]++;
return;
}
bool same(int x, int y){
return root(x) == root(y);
}
int get_cnt(){
return cnt;
}
};
int main() {
ll n,q;
cin >> n >> q;
UnionFind uf(3000);// UnionFindはあり得る最大の頂点数で初期化する
vector<pair<ll,ll>> a;// 頂点を持っておく配列
rep(i,n){
ll x, y;
cin >> x >> y;
a.emplace_back(x,y);
}
priority_queue<Tuple, vector<Tuple>, greater<Tuple>> que;
rep(i,n){
for(int j = i + 1; j < n;j++){
auto [x,y] = a[i];
auto [xx, yy] = a[j];
ll tmp = abs(x - xx) + abs(y - yy);
que.push({tmp,i, j});
}
}
rep(i,q){
int t;
cin >> t;
if(t == 1){
n++;
ll x, y;
cin >> x >> y;
// 新しい頂点と他の頂点の距離を優先度付きキューにいれる
rep(i,n-1){
auto [xx,yy] = a[i];
ll tmp = abs(x - xx) + abs(y - yy);
que.push({tmp, i, n-1});
}
a.emplace_back(x,y);
}else if(t == 2){
if(que.empty()){
cout << "-1" << endl;
continue;
}
while(!que.empty()){
auto [w, x, y] = que.top();
que.pop();
// 頂点ペアが繋がっていなかったら同じ距離のものを全て繋ぐ
if(!uf.same(x,y)){
uf.unite(x,y);
while(!que.empty() && get<0>(que.top()) == w){
auto[ww, xx, yy] = que.top();
que.pop();
if(!uf.same(xx, yy))uf.unite(xx,yy);
}
cout << w << endl;
break;
}
// 全ての頂点が繋がっていた場合は-1
if(uf.get_cnt() == n - 1){
cout << "-1" << endl;
break;
}
}
}else{
ll a,b;
cin >> a >> b;
a--;
b--;
if(uf.same(a,b))cout << "Yes" << endl;
else cout << "No" << endl;
}
}
return 0;
}
まとめ
今回は、コードは単純だけど問題文の読解が難しい問題が多かった気がします。
最近ちょくちょく水パフォが取れているのでこの調子で来月には入水を達成したいです。
拙い記事なので誤り等ありましたらコメントお願いします。