因果推論初学者です。
最近統計的因果探索の最新手法を学ぶ機会があったのですが、基礎的手法であるLiNGAMが分かってないと全く話にならないなと気付いたため、LiNGAMの数式を読み、逐一Pythonで処理を追うことで理解を試みます。LiNGAMの推定には2つのアプローチがありますが、今回は独立成分分析(ICA)によるアプローチを用います。
実装にあたり、統計的因果探索 (機械学習プロフェッショナルシリーズ)の書籍[1]とLiNGAMの論文[2]、そして本家のGithubのコードを参考にしました。
LiNGAMで出来ること
例えば、4つの観測変数$x_1$,$x_2$,$x_3$,$x_4$を持つ$N$個の観測データがあったとします。そのデータから、線形で非巡回で誤差が非ガウス分布に従うような因果グラフを導き出します(下図)。
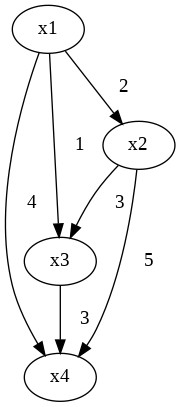
LiNGAMモデル
モデルを数式で示すと次のようになります。
$p$個の観測変数$x_1,x_2,x_3,…,x_p$に対して、LiNGAMモデルは
$$x_i = \displaystyle \sum_{j≠i} b_{i,j} x_j + e_i \qquad i=1,2,...,p\tag{1}$$
ただし$e_i$は誤差変数で、非ガウス連続分布で独立を仮定します。
モデルの行列表現は次のようになります。
$${\bf x} = {\bf Bx} + {\bf e} \tag{2}$$
${\bf B}$は係数行列であり、$p×p$の正方行列です。因果グラフについて非巡回を仮定しているため、観測変数の順序を正しい順序で並び替えると係数行列${\bf B}$は**対角成分がすべて0となる下三角行列(厳密な下三角行列)**となります。
STEP0 人工データの生成
今回は次のような人工データを作って因果グラフを求めてみます。先ほど図で示した因果グラフを基にデータを作ります。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.decomposition import FastICA
from sklearn.linear_model import LassoLarsIC, LinearRegression
from scipy.optimize import linear_sum_assignment
from graphviz import Digraph
# STEP0 人工データ生成
num_of_data = 1000
num_of_features = 4
_B_true = np.asarray([[0,0,0,0], [2,0,0,0], [1,3,0,0], [4,5,3,0]])
e1 = np.random.uniform(size=num_of_data)
e2 = np.random.uniform(size=num_of_data)
e3 = np.random.uniform(size=num_of_data)
e4 = np.random.uniform(size=num_of_data)
x1 = e1
x2 = _B_true[1,0] * x1 + e2
x3 = _B_true[2,0] * x1 + _B_true[2,1] * x2 + e3
x4 = _B_true[3,0] * x1 + _B_true[3,1] * x2 + _B_true[3,2] * x3 + e4
_X = np.asarray([x1, x2, x3, x4]).T
_columns = ["x1", "x2", "x3", "x4"]
# 観測変数をテキトーに並べ替え
order_shuffled = [3,0,2,1]
X = _X[:,order_shuffled]
columns = [_columns[i] for i in order_shuffled]
P_os = np.zeros_like(_B_true)
for i,j in enumerate(order_shuffled):
P_os[i,j] = 1
B_true = P_os@_B_true@P_os.T
DF_X = pd.DataFrame(X,columns=columns)
解となる厳密な下三角行列Bを作った後、観測変数の順序をテキトーに並べ替えます。ここでは、$(x_4,x_1,x_3,x_2)$の順とします。現実世界では本来正しい観測変数の順序なんて分からないためです。
STEP1 復元行列Wの推定
式$(2)$を変形すると、次のようになります。
\begin{align}
{\bf x} &= {\bf (I-B)}^{-1} {\bf e} \\
&= {\bf A} e \tag{3}
\end{align}
ここで、誤差変数ベクトル$\bf e$は独立で非ガウスなので、この式はICAモデルとみなすことが出来、行列$\bf A$の逆行列を復元行列$\bf $とすると$\bf{W=I-B}$となります。ただし、ICAによって求まるものは本来の$\bf W$から行の順序と尺度が異なる可能性のあるものとなります。よって、行の順序の置換行列${\bf P}$と、尺度を示す対角行列$\bf D$を用いて、ICAで推定される復元行列${\bf W_{ICA}}$は
\begin{align}
{\bf W_{ICA}} &={\bf PDW} \\
&= {\bf PD(I-B)} \tag{4}
\end{align}
となります。
それでは、実際にpythonで${\bf W_{ICA}}$を求めてみます。とはいえ、今回はICAがテーマではないので、scikit-learn内のFastICAでサクっと求めてしまいます。
# STEP1 W_ICA(PDW)の推定
ICA = FastICA(random_state=0)
ICA.fit(X)
W_ICA = ICA.components_
STEP2 置換行列Pの推定
式$(4)$を変形すると、次のようになります。
\begin{align}
{\bf P^{-1}W_{ICA}} &={\bf D(I-B)} \tag{5}
\end{align}
ここで、非巡回性より$\bf B$は対角成分は$0$なので、$\bf {I-B}$の対角成分は$1$、さらに尺度行列$\bf {D}$の対角成分は$0$でないので$\bf {D(I-B)}$の対角成分は$0$ではありません。よって、式$(5)$左辺において$\bf W_{ICA}$は対角成分に$0$が来ないような置換がなされなければなりません。よって、そのような置換行列$\bf \tilde{P}$とすると、その推定行列は
\begin{align}
{\bf \hat{\tilde{P}} = \mathop{\rm arg~min}\limits_{\bf \tilde{P}} \sum_{i=1}^p \frac{1}{|(\bf {\tilde{P} \hat{W}_{ICA}})_{ii}| }} \tag{6}
\end{align}
で推定されます。このような置換行列を求める問題は線形割り当て問題と考えられるので、ハンガリアン法等によって解くことが出来ます。
さて、実装ですが、例によってハンガリアン法がテーマじゃないのでscipyでサクっと解いてしまいます。
# STEP2 P_tilde_hatの推定
epsilon = 1e-16
cost = 1 / np.abs(W_ICA + epsilon)
row_ind, col_ind = linear_sum_assignment(cost)
P_tilde_hat = np.zeros_like(W_ICA)
for i,j in zip(row_ind,col_ind):
P_tilde_hat[i,j] = 1
P_tilde_hat = np.linalg.inv(P_tilde_hat)
逆数を取るときに0が現れると爆発してしまうので微小値εを足してます。
STEP3 尺度行列Dの推定
例によって$\bf {I-B}$の対角成分は$1$なので${\bf D(I-B)}$の対角成分は対角行列$\bf D$と同じです。よって、式$(5)$ より対角行列$\bf D$は${\bf P^{-1}W_{ICA}}$の対角成分と等しいと言えます。
よって、$\bf{D}$の推定行列は
\begin{align}
{\bf{\hat D} = diag(\hat{\tilde{P}} \hat{W}_{ICA})} \tag{7}
\end{align}
pythonで書くとこうなります。
# STEP3 D_hatの推定
D_hat = np.diag(np.diag(P_tilde_hat@W_ICA))
STEP4 復元行列Wと係数行列Bの推定
式$(5)$より、復元行列$\bf{W}$を推定行列は
\begin{align}
{\bf \hat W = \hat D^{-1} \hat{\tilde{P}} \hat{W}_{ICA}} \tag{8}
\end{align}
であり、係数行列$\bf{B}$を推定行列は
\begin{align}
{\bf \hat B = I - \hat W} \tag{9}
\end{align}
となります。
# STEP4 W_hat,B_hatの推定
W_hat = np.linalg.inv(D_hat)@P_tilde_hat@W_ICA
I = np.eye(num_of_features)
B_hat = I - W_hat
STEP5 因果的順序(causal order)の推測
ここまでの段階で、式$(2)$で示されるLiNGAMモデル式自体はほぼ求まったも同然なのですが、グラフを書くための因果の方向自体は未知です。よって、式$(2)$の観測変数順序を入れ替えることで$\bf{B}$が厳密な下三角行列となるような置換を発見しなければなりません。つまり、式$(2)$において置換行列$\bf{\ddot{P}}$をかけて
$${\bf \ddot{P} x} = {\bf \ddot{P} Bx} + {\bf \ddot{P} e} \tag{10}$$
$${\bf \ddot{P} x} = {\bf (\ddot{P} B\ddot{P}^{\mathrm{T}})\ddot{P}x} + {\bf \ddot{P} e} \tag{11}$$
このときの$\bf \ddot{P} B\ddot{P}^{\mathrm{T}}$が厳密な下三角行列に可能な限り近くなるような$\bf{\ddot{P}}$を探します。
このような置換行列を力任せ探索で求めてもよいのですが、考えられる置換行列の数は$p!$個のため限度があります。そこで、文献[3]ではこれを高速に求める方法が提案されています。
その手法では、まず$\bf \hat{B}$から絶対値の小さい順から$p(p+1)/2$個の成分を0に置き換えます。その後、観測変数を並び替えて下三角行列になるかどうか判定し、なれば終了、ダメならその次に小さい$\bf \hat{B}$の成分を0に置き換えてもう一度判定します。
下三角行列判定(=因果的順序の推測)方法ですが、
①まず$\bf \hat{B}$のうち成分が全て0の行を$i$行目とします。(存在しなければ判定はFlase)
②$i$を因果順序リストに加えます
③$\bf \hat{B}$の$i$行目と$i$列目を消して、新しい行列$\bf \hat{B}$として①に戻ります
完成した因果順序リストは祖先→孫です。
ではpython実装です。正直この部分は処理がややこしすぎて本家のコードを大いに参考にしました・・・。
# STEP5 因果的順序(causal order)の推測
pos_list = np.vstack(np.unravel_index(np.argsort(np.abs(B_hat), axis=None), B_hat.shape)).T
initial_zero_num = num_of_features * (num_of_features + 1) // 2
for i, j in pos_list[:initial_zero_num]: #p(p+1)/2個0に置換
B_hat[i, j] = 0
Mtx_lowtri = B_hat
causal_order = []
original_index = np.arange(num_of_features)
for i in range(num_of_features): #厳密な下三角行列判定
idx_row_all_zero_list = np.where(np.sum(np.abs(Mtx_lowtri), axis=1) == 0)[0]
if len(idx_row_all_zero_list) == 0:
print("厳密な下三角行列にならない")
break
idx_row_all_zero = idx_row_all_zero_list[0]
causal_order.append(original_index[idx_row_all_zero])
original_index = np.delete(original_index, idx_row_all_zero, axis=0)
mask = np.delete(np.arange(len(Mtx_lowtri)), idx_row_all_zero, axis=0)
Mtx_lowtri = Mtx_lowtri[mask][:, mask]
P_doubledot = np.zeros_like(B_hat)
for i,j in enumerate(causal_order):
P_doubledot[j,i] = 1
今回のデータでは1発で下三角行列になる因果的順序が見つかったのでコードはループしてません。きちんとした実装は本家のものを見てください。
STEP6 仕上げ、枝刈り
データの数が十分のときはSTEP5で導かれる係数行列で問題ありませんが、そうでない場合は枝刈りを最終仕上げとして用いることでモデルが改善されるそうです。
書籍では枝刈り手法の1つとしてAdaptive Lassoを用いることを提案しています。Adaptive Lassoでは、Lasso正則化項に関して$\bf w$で重み付けすることで、変数選択に一致性を持たせます。この$\bf w$は、線形回帰で推定される係数の逆数を用いることが提案されています。STEP5で求めた因果的順序に従って、それぞれの観測変数に関してAdaptive Lassoを行い、最終的な解とします。
実装では、まず線形回帰を行って係数を推定し、推定された係数から重みを求め、Lassoの入力データにその重みをかけて、Lassoの出力である推定量に重みをかければ求まります。
# STEP6 枝刈り
B_pred = np.zeros_like(B_hat, dtype='float64')
lr = LinearRegression()
reg = LassoLarsIC(criterion='bic')
for i in range(1,num_of_features):
#adaptive lasso
predictors = causal_order[:i] #予測変数
target = causal_order[i] #目標変数
lr.fit(X[:, predictors], X[:, target])
weight = 1/(np.abs(lr.coef_) + epsilon)
reg = LassoLarsIC(criterion='bic')
reg.fit(X[:, predictors] * weight, X[:, target])
B_pred[causal_order[i], causal_order[:i]] = reg.coef_ * weight
可視化
最後に、求めたモデルを可視化すると下図のようになります。
左から真のグラフ、STEP5で求めたグラフ、STEP6の処理を行ったグラフです。今回はデータが単純でデータ数も十分用意したため、STEP5の時点で十分上手くいってます。
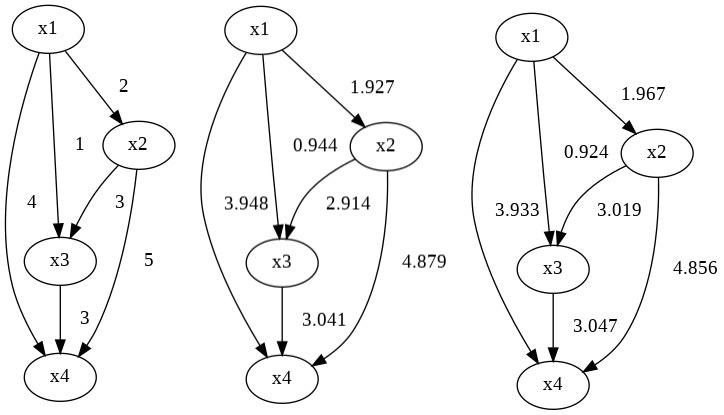
可視化はgraphvizを用いました。グラフ作成のコードは次のものを使いました。
def Make_Graph(columns, B):
Graph = Digraph(format="png")
for i, j in enumerate(columns):
for k, l in enumerate(columns):
if B[i, k] != 0:
Graph.edge(l, j, color="black", label= " " + str(B[i, k].round(3)))
return Graph
おわりに
以上、因果推論初学者が、書籍[1]や論文[2]を照らし合わせ、本家のコードを大いにカンニングし、LiNGAMを頑張って読み解きました。
参考文献とか
[1] 清水 昌平. 統計的因果探索 (機械学習プロフェッショナルシリーズ). 講談社.
[2] Shimizu et al. A linear non-Gaussian acyclic model for causal discovery. Journal of Machine Learning Research 7.Oct (2006): 2003-2030.
[3] Hoyer et al. New permutation algorithms for causal discovery using ICA. In Proceedings of International Conference on Independent Component Analysis and Blind Signal Separation(2006).