はじめに
この記事は株式会社ACCESSのAdvent Calendar 2020の12日目の記事です。
昨年のAdvent Calendarで扱ったPythonの非線形最小二乗法フィッティングライブラリのlmfitについて今年も書くことにします。
lmfitの概要的なところは、昨年の記事 (lmfitでモデルフィッティング) を参考にしてください。
同時モデルフィッティング
この記事では、「同時モデルフィット」というものについて扱います。
この記事でいう「同時」とは、複数のデータセットを同時にモデルでフィッティングすることを指します。
特段理由がなければ、2つのデータセットを別々にモデルフィッティングをして、それぞれの結果としてベストフィットパラメータを得ればよいです。しかし、2つのデータセットが因果関係をもち、その結果としてそれぞれのデータに適応するモデルのパラメータが関係性をもつ場合、その関係性をモデルフィットにも反映したくなります。
例えば、4つの検出器で同じ天体を同時に観測し、4つの検出器それぞれでエネルギースペクトルを取得したとします。しかし、この4つの検出器は、それぞれ特性が異なり、同じ天体のスペクトルが同時に同じだけの光子が入射したとしても、全く同じエネルギースペクトルが得られないとします。この問題を回避するために、天体のスペクトルを表すモデルと、検出器の特性を表すモデルとを組み合わせたモデルで、4つのエネルギースペクトルを同時にモデルフィッティングし、天体のスペクトルを表すモデルのパラメータは、4つのスペクトルに対して共通にし、検出器の特性を表すモデルのパラメータは、4つのデータそれぞれに設けようにします。
筆者はよく、こんなことをX線天文衛星すざく (Mitsuda et al. 2007) に搭載されたX線CCD検出器 XIS (Koyama et al. 2007) によって取得されたX線のエネルギースペクトルをフィッティングするときにやっていました。
I had simultaneously fitted X-ray spectra obtained by four XISs.
同時フィッティングというと"simultaneously"という単語を用いるので、なんか懐かしくなって英文かいちゃいました : )
lmfitで同時モデルフィッティング
データ
今回は、上に書いたような天体のデータを用意せず(面倒だ)、簡単なデータセットをここで用意します。
以下のようなシンプルな形をしたデータセットを用意することにします。ここで、$G(x)$は、正規分布、$C$は定数を表します。
f\left( x \right) = G \left( x \right) + C
import numpy as np
def gauss(x, cen, sigma, amp):
return amp * np.exp(-(x-cen)**2 / (2.*sigma**2))
def const(x, const):
return const
x = np.linspace(0, 2, 150)
d_1 = gauss(x, 1, 0.5, 10) + const(x, 5) + np.random.normal(size=x.size, scale=0.5) # data1
d_2 = gauss(x, 1, 0.5, 10) + const(x, 2.5) + np.random.normal(size=x.size, scale=0.5) # data2
data = np.array([d_1, d_2])
データは2×150の配列で与えている。
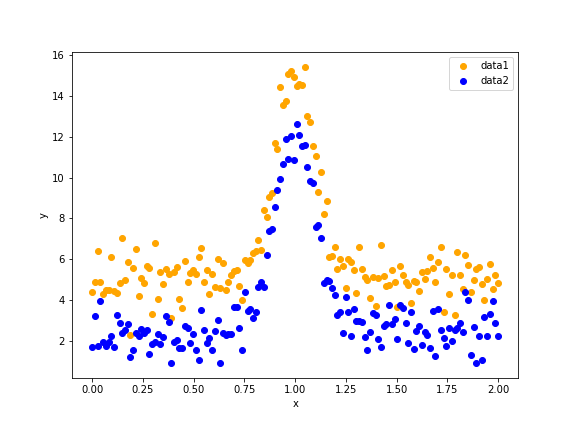
作成したデータをプロットすると以下のようになります。
正規分布のパラメータは、2つのデータセットで同じ値を使用し、定数の値のみ異なるようにしています。
また、ここで作ったデータをフィッティングするので、各データ点に正規分布にしたがったランダムノイズを付加するようにしています。
パラメータ
Parametersクラスオブジェクトを定義する。
import lmfit as lf
# Parameters クラスオブジェクトの宣言
fit_params = lf.Parameters()
# 各パラメータの設定
for i in range(data.shape[0]):
data_id = i+1
fit_params.add(name=f'cen_{data_id}', value=0.5, min=0, max=2)
fit_params.add(name=f'sigma_{data_id}', value=1, min=0, max=10)
fit_params.add(name=f'amp_{data_id}', value=1, min=0, max=100)
fit_params.add(name=f'const_{data_id}', value=0, min=0, max=100)
上でデータを作成するときに、正規分布関数のパラメータの値は、2つのデータセットで同じ値にしていたので、フィッティングするときには、これらのパラメータは2つのデータセット間で共通のパラメータとして扱うようにします。
for param_name in ( 'cen', 'sigma', 'amp' ):
fit_params[f'{param_name}_2'].expr = f'{param_name}_1'
パラメータを設定すると以下のようになる。
| name | value | initial value | min | max | vary | expression |
|---|---|---|---|---|---|---|
| cen_1 | 0.50000000 | 0.5 | 0.00000000 | 2.00000000 | True | |
| sigma_1 | 0.00000000 | 0 | 0.00000000 | 10.0000000 | True | |
| amp_1 | 0.00000000 | 0 | 0.00000000 | 100.000000 | True | |
| const_2 | 0.00000000 | 0 | 0.00000000 | 100.000000 | True | |
| cen_2 | 0.50000000 | 0.5 | 0.00000000 | 2.00000000 | False | cen_1 |
| sigma_2 | 0.00000000 | 0 | 0.00000000 | 10.0000000 | False | sigma_1 |
| amp_2 | 0.00000000 | 0 | 0.00000000 | 100.000000 | False | amp_1 |
フィッティング (目的関数の最小化)
目的関数を定義して、lf.minimize()メソッドを用いて定義した目的関数を最小化する。今回は、最小化の手法としてmethod=leastsq(Levenberg-Marquardt法)を使用する。
method=leastsq を使用する場合、最小化するものを配列でminimize()メソッドに与える必要があるので、 データとモデルの残差の配列を与えればよい。
まずは、与えられたパラメータでのモデルの値を算出するメソッドを定義する。
def calculate_model(params:lf.Parameters, x:np.ndarray, data_id:int):
return gauss(x, cen=params[f'cen_{data_id}'], sigma=params[f'sigma_{data_id}'], amp=params[f'amp_{data_id}']) + const(x, const=params[f'const_{data_id}'])
つづいて、データとモデルの残差を算出するメソッドを定義する。
def objective(params:lf.Parameters, x:np.ndarray, data:np.ndarray):
# make residual per data set
residual = 0.0 * data
for n in range(data.shape[0]):
residual[n] = data[n] - calculate_model(params, x, n+1)
# now flatten this to a 1D array, as minimize() needs
return residual.flatten()
ここでのポイントは、2次配列のデータを1行ごと(データセットごと)にモデルとの残差を求め、最終的にnp.ndarray.flatten()を用いて、1次配列として残差の配列を返すようにしている。また、目的関数として与えるメソッドは、function(params, *args, **kws)として定義する必要があることに注意しましょう。
最後にminimize()メソッドを用いて、目的関数を最小化しましょう。
result = lf.minimize(fcn=objective, params=fit_params, method='leastsq', args=(x, data))
minimize()メソッドの引数argsに、fcnで与えた目的関数のメソッドのparams以外のパラメータをtupleで順位を考慮して与える。argsの代わりにkwsの引数にdictでパラメータ名をdictのkeyとして与えることもできます。詳細は公式ドキュメントを参照してください。
フィッティング結果
以下のように、フィッティング結果のまとめを見られる。
# summary
print(lf.fit_report(result))
[[Fit Statistics]]
# fitting method = leastsq
# function evals = 37
# data points = 300
# variables = 5
chi-square = 73.4565291
reduced chi-square = 0.24900518
Akaike info crit = -412.126605
Bayesian info crit = -393.607693
[[Variables]]
const_1: 4.97696372 +/- 0.04419601 (0.89%) (init = 1)
cen_1: 1.00069722 +/- 0.00134922 (0.13%) (init = 1)
sigma_1: 0.09885423 +/- 0.00142645 (1.44%) (init = 0.1)
amp_1: 10.1194031 +/- 0.12193619 (1.20%) (init = 10)
const_2: 2.52890608 +/- 0.04419602 (1.75%) (init = 1)
cen_2: 1.00069722 +/- 0.00134922 (0.13%) == 'cen_1'
sigma_2: 0.09885423 +/- 0.00142645 (1.44%) == 'sigma_1'
amp_2: 10.1194031 +/- 0.12193619 (1.20%) == 'amp_1'
[[Correlations]] (unreported correlations are < 0.100)
C(sigma_1, amp_1) = -0.473
C(sigma_1, const_2) = -0.246
C(const_1, sigma_1) = -0.246
C(const_1, const_2) = 0.150
C(const_1, amp_1) = -0.147
C(amp_1, const_2) = -0.147
ベストフィットパラメータ値等は以下のプロパティが持っている。
result.chisqr # カイ自乗値
result.nfree # 自由度
result.redchi # 換算カイ自乗値
result.aic # aic
result.bic # bic
result.params['const_1'].value # パラメータの最適値
result.params['const_1'].stderr # パラメータの標準誤差
minimize()メソッドの返り値であるMinimizerResultクラスオブジェクトは、フィッティング結果をプロットするメソッドは用意されていないので、自前でmatplotlib.pyplotを用いてプロットする。
from matplotlib import pyplot as plt
fig, ax = plt.subplots(figsize=(8,6), nrows=2, gridspec_kw={'height_ratios': [2,1]})
ax[0].scatter(x, data[0], color='orange', label='data1')
ax[0].scatter(x, data[1], color='blue', label='data2')
ax[0].plot(x, calculate_model(result.params, x, 1), color='orange', label='model1')
ax[0].plot(x, calculate_model(result.params, x, 2), color='blue', label='model2')
ax[0].set_ylabel('y')
ax[0].tick_params(labelbottom=False)
ax[0].legend()
ax[1].scatter(x, data[0] - calculate_model(result.params, x, 1), color='orange')
ax[1].scatter(x, data[1] - calculate_model(result.params, x, 2), color='blue')
ax[1].set_ylabel('resudual')
ax[1].set_xlabel('x')
ax[1].axhline(0.0, ls='--', color='black')
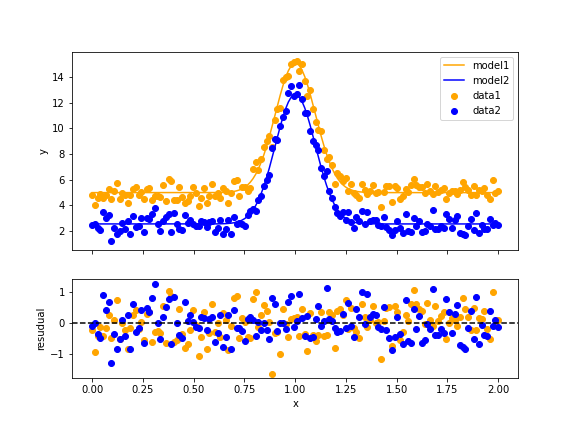
以下のグラフが描画できる。
きれいにフィッティングすることができていることが確認できる。
参考
引き続き、13日目の@SekiTさんの自然数に関する記事をお楽しみください!!