1.はじめに
Python機械学習プログラミング[第2版] という本を買って勉強を始めました。効率的な学習を進める為には、勉強した内容をアウトプットするのが効果的ということで、勉強した内容を備忘録の形でここに残すことを進めています。
なお、本ではコードを一部 jupyter notebook形式で記載しているようですが、ここでは.py形式でも実行できるような形式で記載したいと思います。
今回は、第5章次元削減の中の主成分分析です。
2.主成分分析(wineデータ)
主成分分析の目的は、分散が最大となる方向を複数見つけ出し、寄与率の高いものに絞り込み(次元削減し)、データを新たな空間に射影することです。
まず、テキストにあるコードを実行してみましょう。
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import numpy as np
import matplotlib.pyplot as plt
# データセットの読み込みとサマリー表示
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/'
'machine-learning-databases/wine/wine.data',
header=None)
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash',
'Alcalinity of ash', 'Magnesium', 'Total phenols',
'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins',
'Color intensity', 'Hue',
'OD280/OD315 of diluted wines', 'Proline']
print(df_wine.head())
print()
# データセットのトレーニングデータとテストデータへの分割(7:3)
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
stratify=y, random_state=0)
print('X_train.shape = ', X_train.shape)
print('y_train.shape = ', y_train.shape)
# Xデータの標準化
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)
# 固有値と固有ベクトルの計算
cov_mat = np.cov(X_train_std.T) # 共分散行列を計算
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat) # 共分散行列から固有値と固有ベクトルを計算
print('\nEigenvalues \n%s' % eigen_vals) # 固有値の表示
print('\nEigenvectors \n%s' % eigen_vecs) # 固有ベクトルの表示
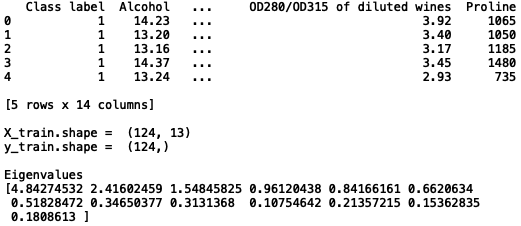

wineデータセットを読み込み、トレインとテストに7:3で分割します。ここで実際に使うのはトレインデータのみです。X_train.shape = (124, 13)なので、13次元のデータが124個あるわけです。
X_trainデータを標準化し、共分散行列(cov_mat)から固有値(Eigenvalues)と固有ベクトル(Eigenvectors)を計算します。13次元のデータなので、固有値は13個、それに対応する固有ベクトルは、13次元のものが13個得られます。
# 主成分のパレート図表示
tot = sum(eigen_vals)
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
plt.bar(range(1, 14), var_exp, alpha=0.5, align='center',
label='individual explained variance')
plt.step(range(1, 14), cum_var_exp, where='mid',
label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal component index')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
# 射影行列wの作成
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) # 固有対(固有値と固有ベクトルのセット)を作成
for i in range(len(eigen_vals))]
eigen_pairs.sort(key=lambda k: k[0], reverse=True) # 固有対のソート
w = np.hstack((eigen_pairs[0][1][:, np.newaxis],
eigen_pairs[1][1][:, np.newaxis])) # 上位2つのベクトルを取得
print('Matrix W:\n', w) # 射影行列w(13行×2列)を表示
# データセットを射影行列wで変換
X_train_pca = X_train_std.dot(w)
# 変換したデータをプロット
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_pca[y_train == l, 0],
X_train_pca[y_train == l, 1],
c=c, label=l, marker=m)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()
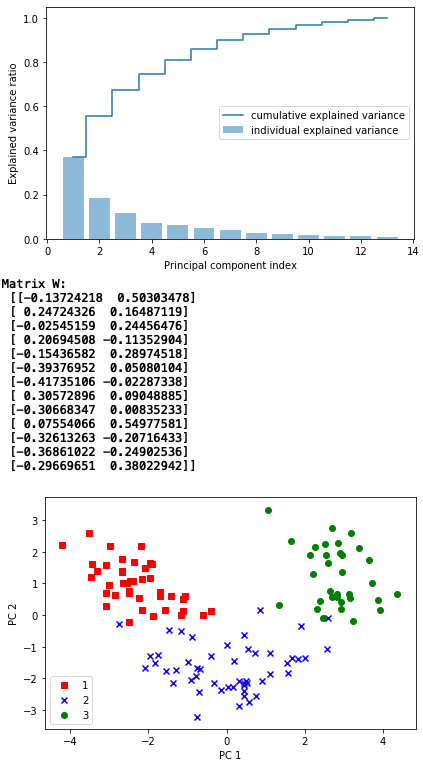
13個ある固有値の個々の大きさは、全体への寄与度を表すので、パレート図にしてみます。折れ線グラフは累積寄与度を表すので、上位2つの固有値で、全体の6割近くに寄与することが分かります。
固有対(固有値と固有ベクトルをセットしたもの)をソートし、上位2つの固有ベクトルを抽出し、射影行列W(13行×2列)を作成します。
13次元のトレイニングデータと2次元の射影行列の内積を取ることで、トレイニングデータが2次元に変換されます。これで、2次元グラフにプロット出来るようになるわけです。
実際に、2次元グラフにプロットすると、一目でこれなら線形分割できそうな感じが分かると思います。
3.主成分分析(irisデータ)
テキストには載っていませんが、シンプルなirisデータセットでも、やってみます。せっかくなので、共分散行列と固有値、固有ベクトルの関係も確認してみましょう。
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
# irisデータセットの読み込み
iris = datasets.load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
stratify=y,
random_state=0)
print('X_train.shape = ', X_train.shape)
print('y_train.shape = ', y_train.shape)
# Xデータの標準化
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)
# 固有値と固有ベクトルの計算
cov_mat = np.cov(X_train_std.T) # 共分散行列を計算
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat) # 共分散行列から固有値と固有ベクトルを計算
print('\ncov_mat \n%s' % cov_mat) # 共分散行列を表示
print('\nEigenvalues \n%s' % eigen_vals) # 固有値の表示
print('\nEigenvectors \n%s' % eigen_vecs) # 固有ベクトルの表示
array = np.array([[eigen_vals[0], 0, 0, 0],
[0, eigen_vals[1], 0, 0],
[0, 0, eigen_vals[2], 0],
[0, 0, 0, eigen_vals[3]]]) # eigen_valsからarrayを作成
print('\narray \n%s' % array)
print('\nEigenvectors(-1) \n%s' % np.linalg.inv(eigen_vecs)) # eigen_vecsの逆行列
results = eigen_vecs.dot(array).dot(np.linalg.inv(eigen_vecs))
print('\nEigenvectors * array * Eigenvectors(-1) = \n%s' % results)

train.shape = (105, 4)なので、トレインデータは4次元です。なので、固有値(Eigenvalues)は4個、固有ベクトル(Eigenvectors)は4次元が4個です。
さて、共分散行列(cov_mat)、固有値(Eigenvalues)、固有ベクトル(Eigenvectors)の関係を見てみましょう。
固有値(Eigenvalues)を対角に入れ、その他を0とした行列を array、固有ベクトル(Eigenvectors)の逆行列を Eigenvectors(-1)とします。
そうすると、共分散行列 = 固有ベクトル * array * 固有ベクトルの逆行列 という関係にあることが分かると思います (*は内積)。ちなみに、ある正方行列をこの様な形に分解することを固有値分解と言います。
さて、この後は、
# 主成分のパレート図表示
tot = sum(eigen_vals)
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
plt.bar(range(1, 5), var_exp, alpha=0.5, align='center',
label='individual explained variance')
plt.step(range(1, 5), cum_var_exp, where='mid',
label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal component index')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
# 射影行列wの作成
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) # 固有対(固有値と固有ベクトルのセット)を作成
for i in range(len(eigen_vals))]
eigen_pairs.sort(key=lambda k: k[0], reverse=True) # 固有対のソート
w = np.hstack((eigen_pairs[0][1][:, np.newaxis],
eigen_pairs[1][1][:, np.newaxis])) # 上位2つのベクトルを取得
print('Matrix W:\n', w) # 射影行列w(4行×2列)を表示
# データセットを射影行列wで変換
X_train_pca = X_train_std.dot(w)
# 変換したデータをプロット
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_pca[y_train == l, 0],
X_train_pca[y_train == l, 1],
c=c, label=l, marker=m)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()
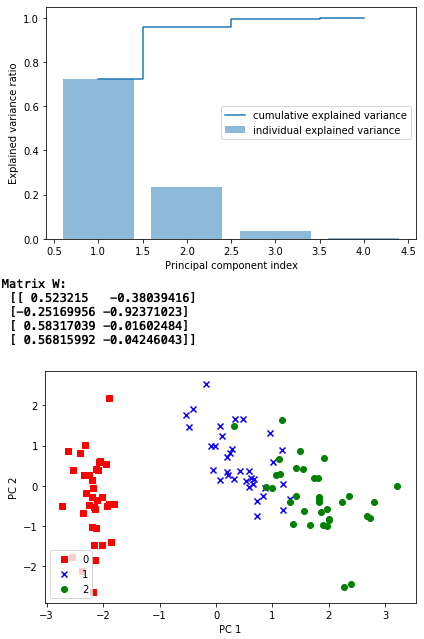
上位2つの固有ベクトルを抽出し、射影行列w(4行×2列)を作成し、トレイニングデータと射影行列の内積を取ると、4次元のトレイニングデータが2次元に変換されます。
2次元に変換されたデータをみると、クラス0は明確に線形分離できそうですが、クラス1と2は少し混じってしまっている感じですね。
4.主成分分析(sklearnライブラリー)
さて、sklearnには、主成分分析(PCA)がライブラリーにあるので、テキストのコードにある様に、これを使ってwineデータを主成分分析し、決定領域を表示をしてみましょう。
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from matplotlib.colors import ListedColormap
# 決定領域表示関数
def plot_decision_regions(X, y, classifier, resolution=0.02):
# setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# plot class samples
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0],
y=X[y == cl, 1],
alpha=0.6,
c=cmap(idx),
edgecolor='black',
marker=markers[idx],
label=cl)
# sklearnによるPCA
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)
lr = LogisticRegression(solver='lbfgs', multi_class='auto') # 引数追加
lr = lr.fit(X_train_pca, y_train)
# 学習データの決定領域表示
plot_decision_regions(X_train_pca, y_train, classifier=lr)
plt.title('PCA for traning_data')
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()
# テストデータの決定領域表示
plot_decision_regions(X_test_pca, y_test, classifier=lr)
plt.title('PCA for test_data')
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()
# 主成分の寄与率表示
pca = PCA(n_components=None)
X_train_pca = pca.fit_transform(X_train_std)
print('\npca.explained_variance_ratio_\n%s' %pca.explained_variance_ratio_)
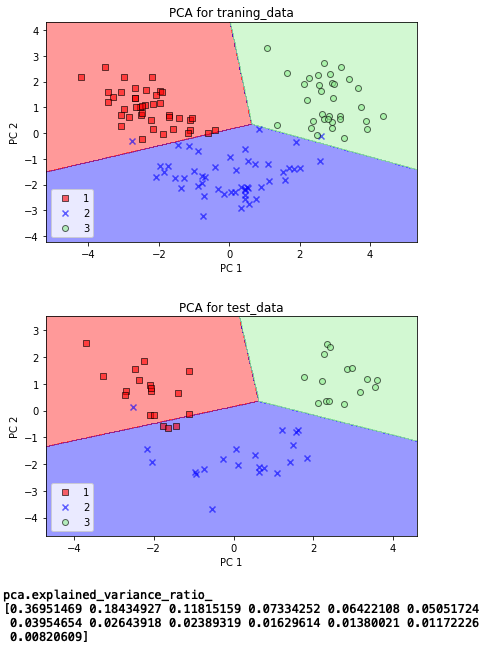
sklearn のライブラリーを使うと簡単ですね。なお、sklearnのバージョン(私が使っているのは 0.21.3)の関係で、テキストのコードのままだとワーニングが出るので、lr = LogisticRegression()に引数を追加しています。