ガウス過程回帰を頑張って理解する

はじめに

経緯

　弊は食品設計を行っているマンです。ベイズ最適化本である「Pythonで学ぶ実験計画法入門 ベイズ最適化によるデータ解析」を参考に、配合物性の最適化を行っている際、「ガウス過程とは・・・？？」と悩みました。

　その際、「ガウス過程と機械学習」という書籍が参考になったため、自身の理解を出力するために、この記事を書きました。n番煎じです。
　なお、本記事ではガウス過程を用いてガウス分布を出力する流れまでしか扱っていませんが、「ガウス過程と機械学習」ではガウス過程のポアソン分布への適用や、測定点数が膨大になった際の計算の省力化などが書いてあります。生物系出身の幣にもわかる解説をしてくださる良い本だと思います。

ガウス過程をやって何がうれしいの？

以下の点が便利です。

• 説明変数の次元に制限がない。（カーネル関数で、ベクトルの内積として処理するため）
• 推定値の不確かさを表現できる
• 非線形な特徴を表現可能（説明変数間の類似度を使用するため）

　ベイズ最適化の一例において、ガウス過程回帰における目的変数の推定値が高く、分散が大きい点（＝データセット内で探索されていない実験点）を探索することで、効率的な実験点の導出が行われています。ベイズ最適化の事例は三井情報株式会社さんの記事がわかりやすいです。

ガウス過程回帰の導出

前処理

　データをオートスケーリングすると後々便利です。オートスケーリングに関しては金子先生の記事がわかりやすいです。
$$ X = { x_1, x_2, \ldots, x_n } $$
のデータがあるとき、$X$ の平均を $\mu$ 、分散を $\sigma^{2}$ とします。
$$ (x_n - \mu)/ \sqrt{\sigma^{2}}$$
と処理することで、$X$ の平均を0、分散を1に変換することができます。説明変数間の尺度 (mPa、kgなど) が違うときにスケールを合わせることができます。当然ですが、オートスケーリングした値は$\sqrt{\sigma^{2}}$でかけて、$\mu$を足すことで元の値に戻すことができます。

導出

わかりやすい線形回帰から考えます。
データ数を $n$、
目的変数を $y$、
$$ y = {{ y_1, y_2, \ldots, y_n }} $$
説明変数を$X$、
$$ X = { x_1, x_2, \ldots, x_n } $$
Xの二乗項など、適当な変換を行う関数 $\phi(X)$ を、
$$ \phi(X) = { \phi_1(X), \phi_2(X), \ldots, \phi_H(X) } $$
特徴量にかける重みを $w$ とします。
$$ w = { w_1, w_2, \ldots, w_H }$$

すると線形回帰は次のように示せます。

\underbrace{
\begin{pmatrix}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{pmatrix}\\
}_{y}
=
\underbrace{
\begin{pmatrix}
\phi_0(x_1), \phi_2(x_1),\ldots, \phi_H(x_1) \\
\phi_0(x_2), \phi_2(x_2),\ldots, \phi_H(x_2) \\
\vdots, {\qquad} {\qquad} {\qquad} {\qquad} \vdots \\
\phi_0(x_n), \phi_2(x_n),\ldots, \phi_H(x_n) \\
\end{pmatrix}
}_{\Phi}
\underbrace{
\begin{pmatrix}
w_0 \\
w_1 \\
\vdots \\
w_H
\end{pmatrix}\\
}_{w}

ここで、 $w$は平均が 0 、分散が $\lambda^{2}I$ の正規分布に従って生成されていると仮定します。ここで $I$ は単位行列を示します。
$$ w \sim \mathcal{N}(0,\lambda^{2}I)$$
すると、ベクトル$w$ を行列$\Phi$で線形変換を行ったものとみなせるため、
$$y = \Phi w $$
も正規分布に従います。($ ➡\sim \mathcal{N}$)

単位行列

➡$m \times m$からなる対角成分が 1、それ以外の要素が 0 の行列

すると、$y(=\Phi w) \sim \mathcal{N}$ の期待値は $w$ の平均が0であるため次のように表せます。
$$\mathbb{E}[y]=\Phi \mathbb{E}[w]=0$$

次に、共分散行列 $\Sigma$を考えます。

共分散

共分散は二つの変数の相関を表します。 $$ a = \{ a_1, a_2, \ldots,a_n \}, \\ b = \{ b_1, b_2, \ldots,b_n \} $$ の$a$と$b$の共分散は $$ \Sigma_{ab} = \frac{1}{n}\sum^n_{i=1}{(a_n - \mu_a)(b_n - \mu_b)} $$

T(転置)

転置は行列の変換方法の一つです。$n \times m$行列を$m \times n$行列へ変換します。

\begin{pmatrix}
1,0,0,0 \\
2,1,0,3 \\
0,0,1,0 
\end{pmatrix}= 
\begin{pmatrix}
1,2,0 \\
0,1,0 \\
0,0,1 \\
0,3,0
\end{pmatrix}^T

\begin{align}\Sigma 
&= \mathbb{E}[yy^{T}] - \underbrace{\mathbb{E}[y]\mathbb{E}[y]^T}_{\mathbb{E}[w]が0であるため、0} \\
&=\mathbb{E}[(\Phi w)(\Phi w)^T] \\
&= \Phi \underbrace{\mathbb{E}[ww^T]}_{ww^Tは\lambda^2 のベクトルとなり\mathbb{E}[ww^T]は対角成分に\lambda^2をもつH \times H 行列となる} \Phi^T \\
&= \lambda^2 \Phi \Phi^T
\end{align}

よって、$y$ は
$$ y \sim \mathcal{N}(0,\lambda^2 \Phi \Phi^T)$$
で表すことができます。ガウス過程回帰では、$w$ を求めずして、$X$同士の関係性（$\Phi \Phi^T$）から$y$ (= $f(X)$)の分布を推測することができます。

ここで、$K = \lambda^2 \Phi \Phi^T$とおくと

K = \lambda^2 \Phi \Phi^T= \lambda^2 \begin{pmatrix} \vdots\\
\phi (x_n)^T \\
\vdots\\
\end{pmatrix}
\begin{pmatrix}
\cdots
\phi(x_n{'})
\cdots
\end{pmatrix}

と表すことができます。
$K$ は$n \times n$ の共分散行列であり、その行列の要素である$k_{nn{'}}$を考えます。

\begin{pmatrix}
k_{11}, \cdots, k_{1n{'}} \\
\vdots {\qquad} {\qquad} \vdots\\
k_{n1}, \cdots, k_{nn{'}}
\end{pmatrix}

k_{nn{'}} = \lambda^2 \underbrace{\Phi(x_n)^T \Phi(x_n{'}) }_{ベクトルの内積＝類似度を示す}

よって、$K$の各要素$k_{nn{'}}$は$\Phi(x_{n})$と$\Phi(x_{1\sim n})$の類似度であり、$K$は$X$間の類似度を格納した行列としてみることができます。

カーネル

では類似度を計算するための$X$の適当な変換($\Phi$)とは何でしょうか？ここでカーネル関数を考えます。カーネル関数 $k(x_n,x_n{'}) $は
$$k(x_n,x_n{'}) = \Phi(x_n)^T \Phi(x_n{'}) $$
を表します。
例えば、よく使われるガウスカーネルを$k(x_n,x_n{'})$にあてはめると
$$k(x_n,x_n{'}) = \theta_1 \exp(\frac{-|x_n - x_n{'}|^2}{\theta_2}) $$
となります。$\theta_1, \theta_2$はハイパーパラメーターです。
$x_n$に関わる項である$\exp(-|x_n - x_n{'}|^2)$だけを考えると、

\begin{align}
\exp(-|x_n - x_n{'}|^2 )
&= \exp\lbrace -(x_n- x_n{'})^2 \rbrace \\
&= \exp\lbrace -(x_n^2+x_n{'}^2) \rbrace \exp \lbrace 2x_nx_n{'} \rbrace \\
&= \exp\lbrace -(x_n^2+x_n{'}^2) \rbrace ( 1+\frac{2x_nx_n{'}}{1!} + \frac{(2x_nx_n{'})^2}{2!}+ \cdots ) \\
&= \exp\lbrace -(x_n^2+x_n{'}^2) \rbrace (1 \cdot 1 + \sqrt{ \frac{2}{1!}}x_n \cdot \sqrt{ \frac{2}{1!}}x_n{'} + \sqrt{ \frac{2^2}{2!}}x_n^2 \cdot \sqrt{\frac{2^2}{2!}} x_n{'}^2 + \cdots)
\end{align}

\begin{align}
\Phi(x_n)   = \exp\lbrace -x_n^2 \rbrace(1, \sqrt{ \frac{2}{1!}}x_n,  \sqrt{ \frac{2^2}{2!}}x_n^2, \cdots)^T
\end{align}

となります。
とはいえ、式展開をするのはめんどくさいので、
$$k(x_n,x_n{'}) = \theta_1 \exp(\frac{-|x_n - x_n{'}|^2}{\theta_2}) $$
に$x_n, x_n{'}$を代入して計算することで、展開後と同様の結果を得ることができます。
上記のような計算の省略をカーネルトリックといいます。

予測値の出力

*「ガウス過程と機械学習」のサポートページを一部改変して使います。
　カーネル関 $K$ が $n \times n$ の類似度の行列であるため、その出力値$f(x_n)$は $x_n$ 間の関係性に依存します。
例えば、$ X = x_1, x_2$ の二点が得られており、その時のカーネル行列が

 \begin{pmatrix}
1,{\quad} 0.8 \\
0.8,{\quad} 1 \\
\end{pmatrix}

の時、$f(x_1)$と$f(x_2)$の値は以下の散布図のようになります。

以下のコードを使って $f(x_n)$ の挙動を確認します。

# matplotlibのTeXレンダラーを無効にする
plt.rc('text', usetex=False)
  
# ガウスカーネル
def kgauss (params):
    [tau,sigma] = params
    return lambda x,y: exp(tau) * exp (-(x - y)**2 / exp(sigma))

# カーネル行列の計算
def kernel_matrix (xx, kernel):
    N = len(xx)
    eta = 1e-6
    return np.array (
        [kernel (xi, xj) for xi in xx for xj in xx]
    ).reshape(N,N) + eta * np.eye(N)

# 平均0, 共分散Kの多次元ガウス分布からランダムサンプリングする
def fgp (xx, kernel):
    N = len(xx)
    K = kernel_matrix (xx, kernel)
    return mvnrand (np.zeros(N), K)

# サンプル点を表示
def scatter_gaussian ():
    xx = np.linspace (xmin, xmax, N)
    for m in range(M):
        f = fgp (xx, kgauss((1,1)))
        plt.scatter (xx, f)
        plot(xx, f)
        plt.xlabel(r"$x_n$")
        plt.ylabel(r"$f(x_n)$")

# x のデータ範囲
xmin,xmax = -5,5
# 観測するデータ点数
N=5
# ランダムサンプリング回数
M=3
# データ点の確認用
print("X: ", np.linspace (xmin, xmax, N))
scatter_gaussian ()

以下の設定の際の出力$f(x_n)$および$N$を変化させた際の出力$f(x_n)$を確認します。

# x のデータ範囲
xmin,xmax = -5,5
# 観測するデータ点数
N=5
# ランダムサンプリング回数
M=3

X:  [-5.  -2.5  0.   2.5  5. ]

# x のデータ範囲
xmin,xmax = -5,5
# 観測するデータ点数
N=25
# ランダムサンプリング回数
M=3

X:  [-5.         -4.58333333 -4.16666667 -3.75       -3.33333333 -2.91666667
 -2.5        -2.08333333 -1.66666667 -1.25       -0.83333333 -0.41666667
  0.          0.41666667  0.83333333  1.25        1.66666667  2.08333333
  2.5         2.91666667  3.33333333  3.75        4.16666667  4.58333333
  5.        ]

測定点数 $n$ が増加するごとに$f(x_n)$が滑らかになっています。
ここまでの流れをまとめると、ガウス過程回帰は、$X = x_1, \ldots, x_n$を基に、$K$を作成、$f \sim \mathcal{N}(0, K)$から$f = f(x_1), \ldots, f(x_n)$ をサンプリングすることで、予測値を得ます。
　ガウス過程回帰では観測点のほかに、観測点間の未観測の点も予測分布を出力させることで、非線形の滑らかな関数を得ています。
　とはいえ、上記のコードではランダムな関数をサンプリングしているため、学習データを用いて、ハイパーパラメーターを学習させる必要があります。

ガウス過程回帰の学習

　学習の前に、ノイズに関して考えます。ノイズ $\epsilon = \epsilon_1, \ldots, \epsilon_n$ が正規分布に従って生成されるとき、$\epsilon$ および $y$ は次の様に示せます。

$$\epsilon = \mathcal{N}(0, \sigma^2) $$
$$y =f(X) + \epsilon$$
よって、$p(y|f)$ は
$$ p(y|f) \sim \mathcal{N}(f, \sigma^2 I)$$
となり、$X$ が与えられた際の$y$ は

\begin{align}
p(y|X) 
&= \underbrace{\int p(y|f)p(f|X)df}_{fについて積分除去} \\
&= \int \mathcal{N}(y|f, \sigma^2I) \mathcal{N}(f|\mu, K)df \\
&= \mathcal{N}(\mu, K+\sigma^2I)
\end{align}

となります。
　そのため、仮にカーネル関数がガウスカーネルであり、それにノイズ$\epsilon$ を加える場合、

\begin{align}
k(x, x') 
&= \theta_1 \exp(\frac{-|x - x'|^2}{\theta_2})+ \sigma^2 \underbrace{\delta(x, x')}_{x=x' の時に1, それ以外では0を返す関数}\\
&= \theta_1 \exp(\frac{-|x - x'|^2}{\theta_2})+ \underbrace{\theta_3}_{\theta_3= \sigma^2に置換}\delta(x, x')
\end{align}

となります。
$$\theta = (\theta_1, \theta_2, \theta_3)$$

　このパラメーター $\theta$ を動かして、評価関数が最小になるように学習を行います。既知データを $D$ 、未知データを

(y^{*}, X^{*})

とし、既知および未知の入力点を合わせて同時にカーネル行列を計算します。

\begin{pmatrix}
y_1\\
\vdots\\
y_n\\
y^{*}
\end{pmatrix}
=
\mathcal{N}
\begin{pmatrix}
\begin{pmatrix}
0 \\
\vdots\\
0 \\
0\\
\end{pmatrix}
,
\begin{pmatrix}
k_{11}, \cdots, k_{1n{'}} , k_{1^*}\\
\vdots {\qquad} {\qquad} \vdots\\
k_{n1}, \cdots, k_{nn{'}}, k_{n^*}\\
k_{^*1}, \cdots, k_{^*n{'}}, k_{^{**}}\\
\end{pmatrix}
\end{pmatrix}

ガウス過程回帰の予測分布は

p(y^{*}|X^{*}, D) = \mathcal{N}(k_{^{*}}^TK^{-1}y, k_{^{**}}-k_{^{*}}^TK^{-1}k_{^{*}}) \\

と示されます。また、精度行列として $\Lambda = K^{-1}$ と置けば、

\mathbb{E}[y^{*}|X^{*}, D] = \sum_{n=1}^Ny_n(\sum_{n'=1}^N\Lambda_{nn'}k(x^{*}, x_{n'}))

となり、各 $y_n$ の値をカーネル関数で重みづけていることで、$x_n$ が近い関係にある $y_n$ の影響を強めていることがわかります。
　そのため、予測分布の平均を用いてクロスバリデーション $R^2$および分散を計算し、評価関数を設計します。その後、この評価関数を最小にするハイパーパラメーター $\theta$ を勾配法で求めます。勾配法のコードはゼロから学ぶディープラーニングから一部拝借します。
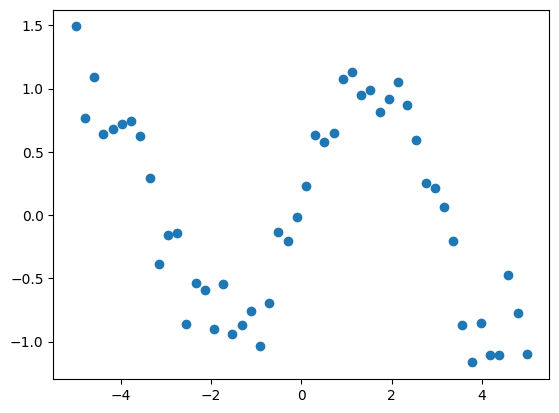
データは正弦波に正規分布のノイズを加えて生成させました。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pylab import *
from numpy.random import multivariate_normal as mvnrand
from sklearn.metrics import r2_score
import random
import tqdm

# おおもとの関数
def gpr_descent (x_train, y_train, kernel, params,lr, step_num):
    init_params = params
    #init_lr =lr
    grad_params, params_hist, r2cv_hist = gradient_descent(init_params, lr= lr, step_num=step_num)
    return grad_params, params_hist, r2cv_hist

# 勾配法を行う関数
def gradient_descent(init_params, lr = lr, step_num= step_num):
    x = init_params
    params_hist =[]
    r2cv_hist = []
    for step in tqdm.tqdm(range(step_num)):
        #lr = lr
        grad, r2cv = numerical_gradient(x)
        x = x- lr*grad
        params_hist.append(x)
        r2cv_hist.append(r2cv)

    return x, params_hist, r2cv_hist

# 勾配法の処理を行う関数, params±h の値の中心微分を計算。
def numerical_gradient(x):
    #極小の値を設定
    h = 1e-4
    #x の長さと同じリストを作成
    grad = np.zeros_like(x)
    r2cv = np.zeros_like(x)
    for idx in range(len(x)):
        tmp_val = x[idx]

        # f(x+h) の計算、fxh1 に値を保存
        x[idx] = tmp_val + h

        fxh1 = Kfold_cv(x_train, y_train, 5, kgauss, x)

        # f(x-h) の計算、fxh2 に値を保存
        x[idx] = tmp_val - h
        fxh2 = Kfold_cv(x_train, y_train, 5, kgauss, x)

        # gradに中心微分を格納
        grad[idx] = (fxh1-fxh2)/(2*h)
        # 値を基に戻す
        x[idx] = tmp_val
        r2cv[idx] = fxh2
    return grad, r2cv

# K fold クロスバリデーションを行う関数
def Kfold_cv(x, y ,  Kfold, kernel, params):
    num_fold = Kfold
    concat_data = np.stack([y, x], 1)
    df= pd.DataFrame(concat_data)
    df_shuffled = df.sample(frac = 1)
    num_unit = int(df.shape[0]/num_fold)
    r2cv = []
    std_list = []
    for i in range(0,num_fold):
        data_test = df_shuffled.iloc[i*num_unit:(i+1)*num_unit, :]
        list_train = [x for x in df_shuffled.index if x not in data_test.index]
        data_train = df_shuffled.iloc[list_train]
        pred, std = gpr(data_test[0], data_train[1], data_train[0], kernel, params)
        std_list.append(std)

        r2cv.append(r2_score(data_test[0], pred))

    # 最小化する評価関数。クロスバリデーションにおけるr2cv の平均からペナルティとして標準偏差を引く。
    obj_metric = -np.mean(np.array(r2cv))+(np.mean(np.array(std_list)/np.max(np.array(std_list))))*0.3


    return obj_metric


# ガウスカーネル
def kgauss (x0, x1):
    [theta1, theta2, theta3] = params
    kernel_value = theta1 * exp (-(x0 - x1)**2 / exp(theta2))+ theta3*(int(x0==x1))
    return kernel_value

# x_testとx_train のカーネル関数を計算
def kv (x, xtrain, kernel):
    return np.array ([kernel(x,xi) for xi in xtrain])

# カーネル行列の計算
def kernel_matrix (xx, kernel):
    N = len(xx)
    eta = 1e-6
    return np.array (
        [kernel (xi, xj) for xi in xx for xj in xx]
    ).reshape(N,N) + eta * np.eye(N)

def gpr (xx, xtrain, ytrain, kernel, params):
    K = kernel_matrix (xtrain, kernel)
    Kinv = inv(K)
    ypr = []; spr = []
    for x in xx:
        s = kernel (x,x)
        k = kv (x, xtrain, kernel)

        ypr.append (k.T.dot(Kinv).dot(ytrain))
        spr.append (s - k.T.dot(Kinv).dot(k))
    return ypr, spr

def gpplot (xx, xtrain, ytrain, kernel, params):
    ypr,spr = gpr (xx, xtrain, ytrain, kernel,params)
    plot (xtrain, ytrain, 'bx', markersize=10, label = "data_point")
    plot (xx, ypr, 'b-', label = "GPR_regression")
    plt.ylim(-5,5)
    fill_between (xx, ypr - 2*sqrt(spr), ypr + 2*sqrt(spr), color='#ccccff')

# データの作成
x_train = np.linspace(-5, 5,50)
y = np.sin(x_train)
y_train = y+np.random.normal(0,0.2, len(x_train))
#plt.plot(x_train, y)
plt.scatter(x_train, y_train)

# 学習
## 初期パラメーター
params = np.array([1, 1, 1])
## 学習率
lr = 0.001
## 学習回数
step_num = 100
grad_params, params_hist, obj_metrics_hist= gpr_descent(x_train =x_train,y_train =  y_train,kernel = kgauss, params = params,lr=  lr,step_num=  step_num)

# params 推移
params_array= np.array(params_hist)
for i in range(params_array.shape[1]):
  plt.plot(params_array[:,i], label=f'theta {i+1}')
plt.xlabel('Iteration')
plt.ylabel('theta[i] Value')
#plt.xscale('log')
#plt.yscale('log')
plt.legend()
plt.grid(True)
plt.show()

# 評価関数推移
obj_metrics_array= np.array(obj_metrics_hist)
for i in range(obj_metrics_array.shape[1]):
  plt.plot(obj_metrics_array[:,i], label=f'objective_values {i+1}')
plt.xlabel('Iteration')
plt.ylabel('objective_values')
#plt.xscale('log')
#plt.yscale('log')
plt.legend()
plt.grid(True)
plt.show()

# GPR可視化
xmin = -10
xmax = 10
N = 100
kernel = kgauss
params = grad_params #[0.1, 0.1, 0.1]
xx = np.linspace (xmin, xmax, N)
gpplot (xx, x_train, y_train, kernel, params)
plot(x_train, y, "--", color = "r", label = "True_function")
plt.legend()

　パラメーターおよび評価関数はステップ数10あたりでプラトー近くまで達していそうです。ガウス過程回帰により、データ密度の高い箇所の分散が小さく、正弦波の特徴をとらえた回帰モデルを作ることができました。よりデータの特徴を捉えるためには線形カーネルなど、様々なカーネルを組み合わせることで、柔軟にガウス過程回帰モデルを調整することでできます。

ベイズ最適化

　ガウス過程回帰（GPR）を用いて、獲得関数の最大化 (最小化) を行う手法です。金子先生の本に様々な獲得関数が書いてあります。今回はその一例として Probability in Target Range(PTR) を書きます。
　PTRは予測されたYが目標の値の範囲に収まる確率です。以下のステップを経て算出されます。

• 未知の入力点 $X^*$ を作成
• GPRにより $y^*$ の予測分布を算出
• 予測分布を目標の値の範囲で積分して確率を算出

　上記のPTRがもっとも大きく算出された未知入力点 $X^*$ を次点の実験候補とすることで、効率的な実験を行うことできます。

まとめ

　ガウス過程回帰を理解するために、自身の学びを出力しました。違っている点など見つかれば適宜修正します。ご指摘いただけると感謝です。