今回はWebGLでレイマーチングを実装します!
n番煎じな記事だと思いますが許してください
今回は、読者の方々にもすぐ実践してもらえるように、WebGL Shader Editorを自作しました。GitHubに上がっているので、よかったらRepositoryにスターをつけたりしてもらえるとモチベが上がって嬉しいです!!
また、今回は実装を主体として扱うので、レイマーチングについての説明はざっくりしかしてません。
詳しいことは他の方の記事に丸投げしています。ご了承ください。
レイマーチング is 何
レイマーチングとは、ポリゴン等を用いずに距離関数を使って様々な形状のオブジェクトを描画する方法です。描画されるシーン全体は板ポリゴンで、その板に対してFragment Shaderと呼ばれるシェーダーを記述し、その中で様々な表現を行います。
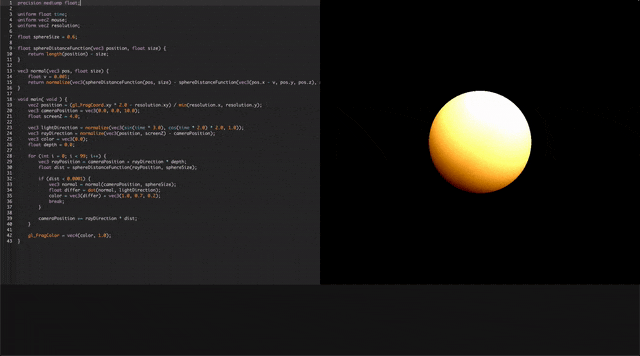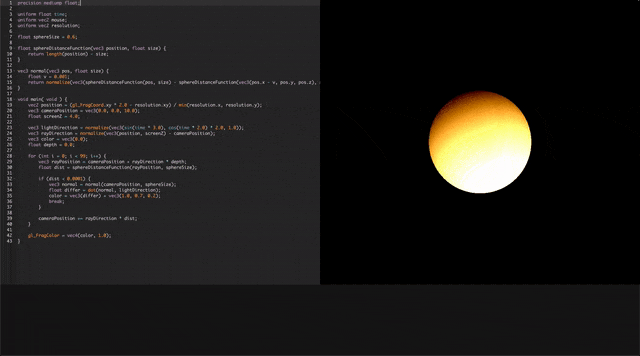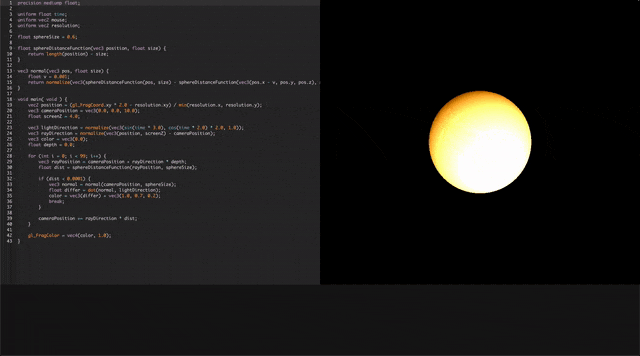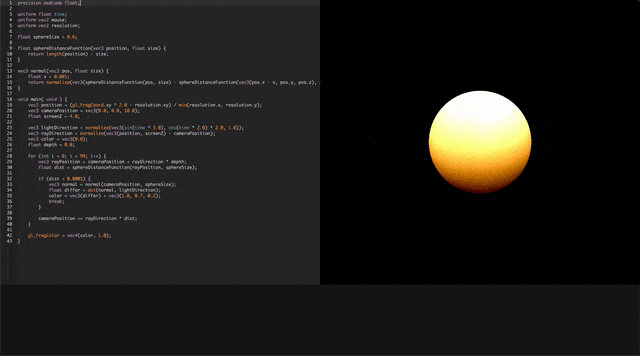
そしてこちらが、今回の完成形です。やっていきましょう。
Let's 実装
GLSLの構文的な解説は端折りますが、
レイマーチングが何故動くかを伝えられるように頑張って説明します。
円を描く
まずはレイを使わずに、距離関数だけを用いて円を描画するだけのコードを書いてみます。
このコードはこれから解説していきますので、一旦「こういうものなんだな〜」と眺めてください。
precision mediump float;
uniform vec2 resolution;
float circle(vec2 p, float r) {
return length(p) < r ? 1.0 : 0.0;
}
void main() {
vec2 position = (gl_FragCoord.xy * 2.0 - resolution.xy) / min(resolution.x, resolution.y);
vec3 color = vec3(circle(position, 0.5));
gl_FragColor = vec4(color, 1.0);
}
これを先程のEditorに貼り付けてCtrl + EnterまたはCommand + Enterで実行すると、
このような結果が得られると思います。
では、何故白い円が描かれたのかを説明します。魔術は使ってません。
まずGLSLの組み込み変数gl_FragCoordは2次元ベクトルで現在の座標を持っています。Fragment Shaderは、全部のピクセルに対してmain関数の中身を実行しています。そのため、この値が処理の度に変化します。
すなわち、自分の座標が円の半径に入っていれば白、外側なら黒ということを実装すれば白い円が描画できます。そこで円の内側であるかどうかを判定する距離関数circle()を実装しています。circle()の中身は単純で組み込み関数length()を用いて原点との距離を取得します。その距離がr未満なら1.0そうでなければ0.0を返す処理をしています。あとはgl_FragColorに取得した値を投げると、円が描画できるわけです。簡単ですね。
ちなみに、GLSLの座標系がちょっと変わっていて、左下が(0, 0)になっています。
そのためlength(gl_FragCoord.xy)を愚直に実装すると左下に円が描画されてしまいます。
この問題を解決するために、
vec2 position = (gl_FragCoord.xy * 2. - resolution.xy) / min(resolution.x, resolution.y);
main()の1行目にこのような処理をはさみ、画面の中央が(0, 0)になるよう座標を正規化しています。
このように現在の座標からオブジェクトとの衝突判定を行う関数を距離関数と呼びます。今回実装した距離関数は最も単純なもので、半径をとるだけですが、複雑な実装をこなすことで、様々な形状のオブジェクトを描画することができます。
レイを定義する
さて、シェーダーがどのように処理されて描画されるのかが伝わったと思います。次にレイを実装して球体を描画していきます。現実の空間を想像してもらえるとわかりやすと思いますが、カメラ(視点)が存在していて、その方向に光を飛ばしオブジェクトに当たると色が確定して描画される、という処理をします。当たり判定には先程の距離関数を用います。
ということでまた先にコードを貼ります。このコードではレイを定義して球体を描画しています。
precision mediump float;
uniform vec2 resolution;
float sphereSize = 0.6;
float sphereDistanceFunction(vec3 position, float size) {
return length(position) - size;
}
void main( void ) {
vec2 position = (gl_FragCoord.xy * 2.0 - resolution.xy) / min(resolution.x, resolution.y);
vec3 cameraPosition = vec3(0.0, 0.0, 10.0);
float screenZ = 4.0;
vec3 rayDirection = normalize(vec3(position, screenZ) - cameraPosition);
vec3 color = vec3(0.0);
for (int i = 0; i < 99; i++) {
vec3 rayPosition = cameraPosition + rayDirection;
float dist = sphereDistanceFunction(rayPosition, sphereSize);
if (dist < 0.0001) {
color = vec3(1.0);
break;
}
cameraPosition += rayDirection * dist;
}
gl_FragColor = vec4(color, 1.0);
}
こちらのコードを実行すると、このような結果が得られると思います。
多くの方はきっと「さっきと何が変わった???????」と困惑していると思いますが、
大丈夫です。安心してください、(レイマーチング)してますよ!
本当に球体かどうか疑問を抱くのはライティングが均一で立体感がないからです。それは次の法線を用いてライティングで解説をするので、まずはレイの定義と実行についてを説明していきます。確かに、一見するとただコードが長くなったのにさっきと結果が変わらないじゃん…という印象を抱きますが、実はレイがびゅんびゅん飛ばされていて、しっかり球体が描画されています。
まずは怖がらず、レイを使う前と後で変わったところを見ていきます。
// カメラが追加された、怖い
vec3 cameraPosition = vec3(0.0, 0.0, 10.0)
float screenZ = 4.0;
// rayって付いてるからレイが定義されている、こわい
vec3 rayDirection = normalize(vec3(position, screenZ) - cameraPosition);
vec3 color = vec3(0.0);
// 謎のfor文が追加されている、怖い
for (int i = 0; i < 99; i++) {
vec3 rayPosition = cameraPosition + rayDirection;
float dist = sphereDistanceFunction(rayPosition, sphereSize);
if (dist < 0.0001) {
color = vec3(1.0);
break;
}
cameraPosition += rayDirection * dist;
}
怖いですね… ![]() 怖くないです。
怖くないです。
まずは視点を定義するという話で、カメラの位置を3次元ベクトルで定義しています。カメラは(0, 0, 10)に設置されています。そして、rayDirectionはレイを飛ばす方向です。正規化した2次元ベクトルとスクリーンのZ座標を渡して3次元ベクトルを作り、そこからカメラの座標を引くことでレイの方向を決めています。
そしてこのfor文がレイをすすめる処理です。レイというのは光線で、視点の方向に一定距離ずつ進みます。進むたびに距離関数を用いてオブジェクトとの距離を計算します。
if (dist < 0.0001) { ... }
ここで、for内部のif文にこの様な処理がありますが、ここが当たり判定で、値が0に近いほど衝突しているとみなして、オブジェクトとの接触状態を確定します。さて、レイの進め方なのですが、カメラの座標にレイの方向を足し、距離を計算、次にカメラの座標をレイの方向と距離の積すすめるという処理をしています。それを最大99回繰り返し、その途中で距離が閾値未満になったら衝突し、色を白にしています。この99がレイマーチングのループ回数で、この値を大きくするほど遠くのオブジェクトまで描画することができます。
このようにしてレイを用いて球体のオブジェクトを描画することができました。難しそうに見えて、実はそうでもないということが伝わっていれば嬉しいです。
法線を用いてライティング
さて、のっぺりした描画とはオサラバします。いよいよライティング(光源処理)を行い、立体に見える物ができます。こちらが今回のコードです。
precision mediump float;
uniform vec2 resolution;
float sphereSize = 0.6;
float sphereDistanceFunction(vec3 position, float size) {
return length(position) - size;
}
vec3 normal(vec3 pos, float size) {
float v = 0.001;
return normalize(vec3(sphereDistanceFunction(pos, size) - sphereDistanceFunction(vec3(pos.x - v, pos.y, pos.z), size), sphereDistanceFunction(pos, size) - sphereDistanceFunction(vec3(pos.x, pos.y - v, pos.z), size), sphereDistanceFunction(pos, size) - sphereDistanceFunction(vec3(pos.x, pos.y, pos.z - v), size)));
}
void main( void ) {
vec2 position = (gl_FragCoord.xy * 2.0 - resolution.xy) / min(resolution.x, resolution.y);
vec3 cameraPosition = vec3(0.0, 0.0, 10.0);
float screenZ = 4.0;
vec3 lightDirection = normalize(vec3(0.0, 0.0, 1.0));
vec3 rayDirection = normalize(vec3(position, screenZ) - cameraPosition);
vec3 color = vec3(0.0);
float depth = 0.0;
for (int i = 0; i < 99; i++) {
vec3 rayPosition = cameraPosition + rayDirection * depth;
float dist = sphereDistanceFunction(rayPosition, sphereSize);
if (dist < 0.0001) {
vec3 normal = normal(cameraPosition, sphereSize);
float differ = dot(normal, lightDirection);
color = vec3(differ);
break;
}
cameraPosition += rayDirection * dist;
}
gl_FragColor = vec4(color, 1.0);
}
では早速実行してみましょう!
立体的〜〜〜!な球体が、描画されたと思います。ライティングが追加され、陰影がはっきりしました。一気に立体感が増してきました。が、そこまで複雑な処理は追加してません。レイは先程定義しました。ですので、怖がらずに見ていきましょう。
// 謎の関数
vec3 normal(vec3 pos, float size) {
float v = 0.001;
return normalize(vec3(sphereDistanceFunction(pos, size) - sphereDistanceFunction(vec3(pos.x - v, pos.y, pos.z), size), sphereDistanceFunction(pos, size) - sphereDistanceFunction(vec3(pos.x, pos.y - v, pos.z), size), sphereDistanceFunction(pos, size) - sphereDistanceFunction(vec3(pos.x, pos.y, pos.z - v), size)));
}
void main( void ) {
// lightってあるから光っぽい怖い
vec3 lightDirection = normalize(vec3(0.0, 0.0, 1.0));
// 深そう
float depth = 0.0;
for (int i = 0; i < 99; i++) {
// 深そう真相は如何に
vec3 rayPosition = cameraPosition + rayDirection * depth;
if (dist < 0.0001) {
// 謎の関数が使われて謎の処理をしている
vec3 normal = normal(cameraPosition, sphereSize);
float differ = dot(normal, lightDirection);
color = vec3(differ);
}
}
}
まずは今回追加した部分です。
まず、lightDirectionは光源の方向で(0, 0, 1)を向いています。depthは深度です。値が大きくなるほど浅くなります。そして一番大事な部分が関数normal()です。
vec3 normal(vec3 pos, float size) {
float v = 0.001;
return normalize(vec3(
/* x */ sphereDistanceFunction(pos, size) - sphereDistanceFunction(vec3(pos.x - v, pos.y, pos.z), size),
/* y */ sphereDistanceFunction(pos, size) - sphereDistanceFunction(vec3(pos.x, pos.y - v, pos.z), size),
/* z */ sphereDistanceFunction(pos, size) - sphereDistanceFunction(vec3(pos.x, pos.y, pos.z - v), size)
));
}
レイの座標をposに渡して(x, y, z)をvの値だけずらす微分を行っています。そうして得られた3次元ベクトルの値を組み込み関数normalize()を用いて正規化しています。その値を法線として返しています。
ここでnormal()が第1引数にレイの座標、第2引数に球体のサイズを渡すと法線ベクトルを返す関数である事がわかりました。レイが衝突した際の処理をもう一度見てみましょう。
vec3 normal = normal(cameraPosition, sphereSize);
float differ = dot(normal, lightDirection);
color = vec3(differ);
sphereSizeは頭で定義してる定数で0.6が入っています。つまり、カメラの座標(レイの座標)と球体の大きさを渡しています。次にdifferに法線ベクトルと光源のベクトルの内積を組み込み関数dot()を用いて取得しています。最後にその値を色として出力しています。このようにして、法線ベクトルを求めて無事ライティングすることに成功しました。
着色とアニメーション
さて、もうレイマーチングは実装しましたし、法線ベクトルを用いたライティングも実装しました。なので最後は味付けをしていこうと思います。まずは球体に色を付けます。と言っても、とても簡単ですのですぐに終わります。
color = vec3(differ) + vec3(1.0, 0.7, 0.2);
先程の色を確定する処理に新しい3次元ベクトルを加算してあげれば色がつけられます。
(r, g, b) = (1, 0.7, 0.2)を加算しました。これで、オレンジっぽい色になります。
たったこれだけです。
次に光を動かします。
これも簡単で光の方向を時間に合わせて動かすだけです。
vec3 lightDirection = normalize(vec3(sin(time * 3.0), cos(time * 2.0) * 2.0, 1.0));
現在の時間をtimeで取得して三角関数で動かしているだけです。
簡単な味付けは以上になります。そしてついに完成しました!!
Fun.
複製してみる(おまけ)
おまけパートとして、球体を複数描画してみたいと思います。まずは完成のコードから。
precision mediump float;
uniform float time;
uniform vec2 resolution;
float sphereSize = 0.6;
vec3 trans(vec3 p){
return mod(p, 6.0) - 2.0;
}
float sphereDistanceFunction(vec3 position, float size) {
return length(trans(position)) - size;
}
vec3 normal(vec3 pos, float size) {
float ep = 0.001;
return normalize(vec3(sphereDistanceFunction(pos, size) - sphereDistanceFunction(vec3(pos.x - ep, pos.y, pos.z), size), sphereDistanceFunction(pos, size) - sphereDistanceFunction(vec3(pos.x, pos.y - ep, pos.z), size), sphereDistanceFunction(pos, size) - sphereDistanceFunction(vec3(pos.x, pos.y, pos.z - ep), size)));
}
void main( void ) {
vec2 position = (gl_FragCoord.xy * 2.0 - resolution.xy) / min(resolution.x, resolution.y);
vec3 cameraPosition = vec3(0.0, 0.0, 10.0);
float screenZ = 4.0;
vec3 lightDirection = normalize(vec3(sin(time * 3.0), cos(time * 2.0) * 2.0, 1.0));
vec3 rayDirection = normalize(vec3(position, screenZ) - cameraPosition);
vec3 color = vec3(0.0);
float depth = 0.0;
for (int i = 0; i < 99; i++) {
vec3 rayPosition = cameraPosition + rayDirection * depth;
float dist = sphereDistanceFunction(rayPosition, sphereSize);
if (dist < 0.0001) {
vec3 normal = normal(cameraPosition, sphereSize);
float diffalent = dot(normal, lightDirection);
color = vec3(diffalent) + vec3(1.0, 0.7, 0.2);;
break;
}
cameraPosition += rayDirection * dist;
}
gl_FragColor = vec4(color, 1.0);
}
modを用いた複製方法です。以下実行画像ですが、集合体恐怖症の方は少し閲覧注意です。
まとめ
この記事を読んだ皆さんはレイマーチングを完全に理解したはずです。できてなかったら、ぼくの解説力が ![]() なので謝ります。今回は球体だけを描画しましたが、シェーダー芸人と呼ばれる人たちは恐ろしいものをたくさん作っています。とても楽しいので、ぜひWebGLでレイマーチングを始めましょう!
なので謝ります。今回は球体だけを描画しましたが、シェーダー芸人と呼ばれる人たちは恐ろしいものをたくさん作っています。とても楽しいので、ぜひWebGLでレイマーチングを始めましょう!あとリゼロはいいぞ(タイトルの伏線回収)
参考記事
レイマーチングがわかりやすく解説されているサイトです
・レイマーチングで球体を描く by doxasさん
・[GLSL] レイマーチング入門 vol.1 by edo_m18さん