標本平均の分散が母分散/標本サイズとなることを数値実験で確認する

背景

標本平均の期待値が母平均となることを数値実験で確認するの続編です。

今回は標本分散$s^2$が$\sigma^2/n$となることを数値実験で確認します($\sigma^2$:母分散、$n$:標本サイズ)。

数値実験

確率分布関数は一次元の一様分布[-1,+1)とします。標本サイズnをパラメータとし、1000回抽出を繰り返し、標本平均の分散値を計算しました。

#include <iostream>
#include <random>

int main(int argc, char **argv)
{
        std::mt19937 mt(0);
        double a = -1, b = 1;
        std::uniform_real_distribution<double> r(a, b);

        int num_of_sample = atoi(argv[1]);//標本サイズ
        int Iter = 1000;//試行回数

        double mean = 0;
        double var = 0;
        for (int iter = 0; iter < Iter; iter++)
        {
                double avr = 0;//標本平均
                for (int n = 0; n < num_of_sample; n++)
                {
                        double val = r(mt);
                        avr += val / (double)num_of_sample;
                }
                mean += avr / (double)(Iter + 1);
                var += avr * avr / (double)(Iter + 1);
        }
        var -= mean * mean;
        std::cout <<  num_of_sample << " " << var << std::endl;

        return 0;
}

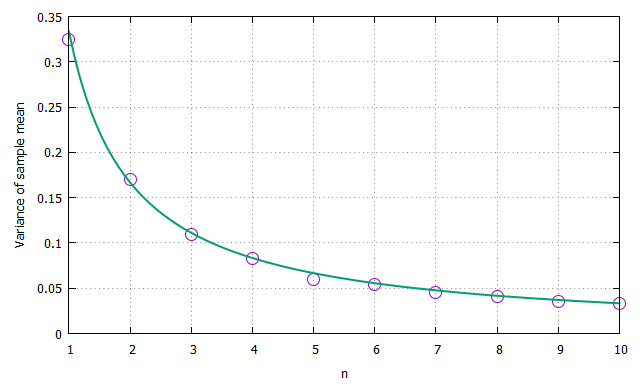
実線が$\sigma^2/n$です。ほぼ理論曲線に乗りました。

まとめ

標本平均の分散が母分散/標本サイズとなることを数値実験で確認することが出来ました。次回は標本分散の期待値を考えたいと思います。
次回：標本分散の期待値が母分散×(標本サイズ-1)/標本サイズとなることを数値実験で確認する