標本平均の期待値が母平均となることを数値実験で確認する

背景

最近、数理統計学の勉強を始めました。紙とペンで計算を追うのも楽しいのですが、数値実験も楽しいし、よい勉強になるので、少しずつ遊んでみることにしました。

まずは準備体操として、標本平均の期待値が母平均となることを数値実験で確認してみます。

数値実験

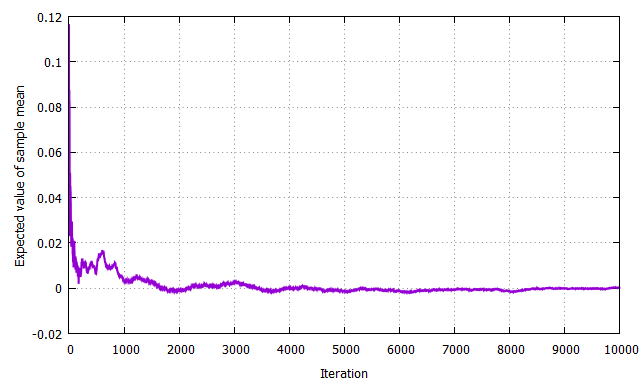
言語はC++を用います。確率分布関数は一次元の一様分布[-1,+1)とします。標本サイズは10とし、10000回抽出を繰り返し、標本平均の平均値が収束することを確認しました。

# include <iostream>
# include <random>

int main()
{
	std::mt19937 mt(0);
	double a = -1, b = 1;
	std::uniform_real_distribution<double> r(a, b);

	int num_of_sample = 10;//標本サイズ
	int Iter = 10000;//試行回数

	double sum = 0;
	for (int iter = 0; iter < Iter; iter++)
	{
		double avr = 0;//標本平均
		for (int n = 0; n < num_of_sample; n++)
		{
			avr += r(mt) / (double)num_of_sample;
		}
		sum += avr;

		std::cout << iter << " " << sum / (double)(iter + 1) << std::endl;
	}

	return 0;
}

母平均0に収束することが確認できました。

まとめ

標本平均の期待値が母平均となることが数値的に確認できました。標本サイズを変えたり、確率分布を変えたりして試してみてもよいですね（というか本来はすべき）。
次回：標本平均の分散が母分散/標本サイズとなることを数値実験で確認する