標本分散の期待値が母分散×(標本サイズ-1)/標本サイズとなることを数値実験で確認する

背景

標本平均の分散が母分散/標本サイズとなることを数値実験で確認するの続編です。
今回は標本分散の期待値が$\sigma^2\times(n-1)/n$となることを数値実験で確認します($\sigma^2$:母分散、$n$:標本サイズ)。

数値実験

言語はC++を用います。確率分布関数は一次元の一様分布[-1,+1)とします。標本サイズは10とし、3000回抽出を繰り返し、標本分散の平均値が収束することを確認しました。

# include <iostream>
# include <random>

int main(int argc, char **argv)
{
        std::mt19937 mt(0);
        double a = -1, b = 1;
        std::uniform_real_distribution<double> r(a, b);

        int num_of_sample = atoi(argv[1]);//標本サイズ
        int Iter = 3000;//試行回数

        double sum = 0;
        for (int iter = 0; iter < Iter; iter++)
        {
                double avr = 0;//標本平均
                double avr2 = 0;//二乗平均
                for (int n = 0; n < num_of_sample; n++)
                {
                        double val = r(mt);
                        avr += val / (double)num_of_sample;
                        avr2 += val*val / (double)num_of_sample;
                }
                sum += avr2 - avr*avr;
                std::cout << iter << " " << sum/(double)(iter+1) << std::endl;
        }

        return 0;
}

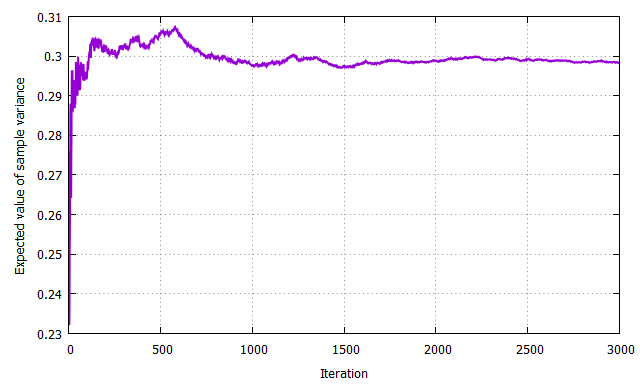
一様分布の母分散は$\sigma^2 = (b-a)^2/12=1/3$、標本分散の期待値はこれに$(10-1)/10$倍したものとなるはずであり、正しい値に収束している様子が確認できました。

まとめ

標本分散の期待値が母分散×(標本サイズ-1)/標本サイズとなることを数値実験で確認しました。つまり標本分散の期待値は母分散よりも小さい値となります。標本分散の値から母分散の値を推定する場合は注意が必要であり、ここから不偏分散という概念があらわれます。