NTT データ数理システムでリサーチャーをしている大槻 (通称、けんちょん) です。
今回はソートについて記します。
0. はじめに
データ構造とアルゴリズムを学ぶと一番最初に「線形探索」や「ソート」が出て来ます。これらのテーマは応用情報技術者試験などでも頻出のテーマであり、アルゴリズムの Hello World とも呼ぶべきものです。
特にソートは、
- 計算量の改善 ($O(n^2)$ から $O(n\log{n})$ へ)
- 分割統治法
- ヒープ、バケットなどのデータ構造
- 乱択アルゴリズムの思想
といった様々なアルゴリズム技法を学ぶことができるため、大学の授業でも、アルゴリズム関連の入門書籍でも、何種類ものソートアルゴリズムが詳細に解説される傾向にあります。本記事でも、様々なソートアルゴリズムを一通り解説してみました。
しかしながら様々な種類のソートを勉強するのもよいが、「ソートの使い方」や「ソートの使いどころ」について強調して学べるものがあった方がよいのではないかと考えています。特にソートアルゴリズムをとりまく環境はここ数十年で大きく変わりました:
| 昔 | 現在 | 変化による影響 | 備考 |
|---|---|---|---|
| ライブラリが充実していなかった | C++ の std::sort() をはじめ、ライブラリが充実している | ソートの種類よりも使いどころが重要になって来ている | |
| メモリが贅沢に使えなかった | メモリが贅沢に使える | 「内部ソート」の重要性は過去のものに | 組込系などでは依然として重要です |
| オブジェクト指向などやりづらかった | 簡単にオブジェクト指向ができる | 「安定ソート」の重要性は薄れている | 組込系などでは現在も重要かもしれません |
こうした時代の変化により、「どういう場面でどのソートが最強か」という議論の重要性が相対的に下がって来ています。昔は
【Before】
- 多くの場面では、クイックソートがよい
- 要素数が小さいときや、ほとんど整列済みに近いときは、挿入ソートも有力
- 要素数が小さくて、省メモリ性や安定性を重視したいときは、挿入ソートがよい
- 各要素が整数値であまり大きな絶対値をとらないときは、計数ソートや基数ソートもよい
- 安定かつ高速なソートが欲しいときは、マージソートがよい
といった議論が盛んに行われて来ました。しかし現代では、優れたソートライブラリを手軽に使用できるようになったり、「安定性」や「メモリ消費量」のことをあまり気にしなくて良くなったりしたため、
【After】
- 大体の場面では、既存のライブラリを使えばよい
- 要素が整数値であまり大きな絶対値をとらないときは、計数ソートや基数ソートもよい
といった程度の認識で十分になって来ています。既存の優れたライブラリとして、例えば C++ の std::sort() はクイックソートをベースとしながらも最悪時の計算量も $O(n\log{n})$ になるように工夫されていて、その他様々な高速化の工夫が施されています。実際、著者の環境でサイズ $n = 10,000,000$ 程度の配列に対して C++ の std::sort() とナイーブなクイックソートとを比較すると、std::sort() の方が 1.5 倍程度速かったです。
こうした時代の変化に対応したソートの入門資料があってもよいのではないかと考えて、本記事を執筆してみました。
0-1. ソートの性質などまとめ
本記事で登場するソートについて最初にまとめます。計算量、内部ソート、安定ソートの意味は下の方で解説しています。
| ソート | 平均計算量 | 最悪計算量 | 内部ソートか | 安定ソートか | 備考 |
|---|---|---|---|---|---|
| 挿入ソート | $O(n^2)$ | $O(n^2)$ | ◯ | ◯ | 初等整列法としてまずまずの性能です、ほとんど整列しているデータには強くて $O(n)$ で動作します |
| マージソート | $O(n\log{n})$ | $O(n\log{n})$ | × | ◯ | 最悪でも $O(n\log{n})$ と強いです |
| クイックソート | $O(n\log{n})$ | $O(n^2)$ | ◯ | × | 最悪では $O(n^2)$ ですが多くの場合高速です |
| ヒープソート | $O(n\log{n})$ | $O(n\log{n})$ | ◯ | × | オンライン処理に強いです |
| 計数ソート | $O(n + A)$ | $O(n + A)$ | × | ◯ | ソートしたい値が $1$ 〜 $A$ の整数のとき。$A$ が小さいときは有力です |
| 基数ソート | $O(n\log{A})$ | $O(n\log{A})$ | × | ◯ | 計数ソートを発展したものです、ソート対象が $0$~$A$ の整数値のとき |
| 選択ソート | $O(n^2)$ | $O(n^2)$ | ◯ | × | 発想は自然ですが遅いです。ヒープソートは選択ソートの思想を引き継いで高速化したものとも言えそうです |
| バブルソート | $O(n^2)$ | $O(n^2)$ | ◯ | ◯ | 遅いですが多くの亜種を生んでいます。コムソートはバブルソートの思想を引き継いで高速化したものと言えそうです |
| シェイカーソート | $O(n^2)$ | $O(n^2)$ | ◯ | ◯ | |
| ノームソート | $O(n^2)$ | $O(n^2)$ | ◯ | ◯ | |
| シェルソート | gap sequence に依存、うまく選ぶと最悪でも $O(n(\log{n})^2)$ にできます | gap sequence に依存 | ◯ | × | 未解決問題を孕んだミステリアスなソートです。挿入ソートの思想を引き継いで高速化したものと言えそうです |
| コムソート | - | $O(n^2)$ | ◯ | × | バブルソートに少し毛を生やして改良したようなソートで実装が超お手軽ですが、その割に超高速です。平均計算量は実験的にはほぼ $O(n\log{n})$ と言われています。 |
| ボゴソート | $O(nn!)$ | ◯ | × | ネタです |
0-2. ソートを学べるオンライン教材
本記事に準拠した、ソートアルゴリズムを学べるオンライン教材を作ってみました。ソートの使い方から、ソートアルゴリズムの詳細まで、段階的に学べる教材としました。
1 問 1 問は下図のような構成になっています。各問題に対して、ユーザが実装したプログラムを提出すると、その場でサーバー上で実行し、正しく挙動したかどうかをジャッジするものです。ぜひ併せて活用してみてください。
0-3. ソートの可視化
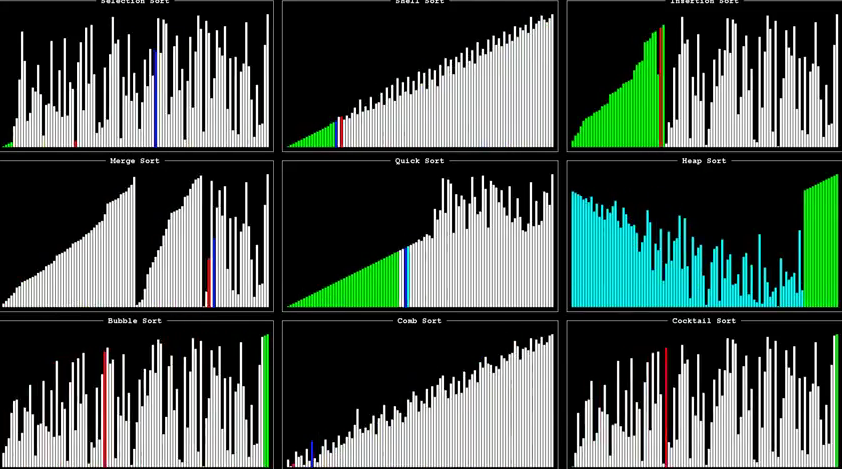
本記事で取り上げるソートアルゴリズム達の動きを可視化した、非常に面白い動画があります!
また一度に 9 つのソートを可視化して比較したものとして
があります。
1. ソートとは
ソートアルゴリズムは「小さい順に並び替える」アルゴリズムです。
(12, 66, 3, 23, 51, 89, 15, 37)
といった配列を
(3, 12, 15, 23, 37, 51, 66, 89)
と小さい順に並び替えます。必ずしも「小さい順」でなくてもよいですし、数値でなくてもよいです。
- 数値を大きい順に
- (3, 1, 9, 4) -> (9, 4, 3, 1)
- 数値のペアを辞書順に
- ((2, 70), (3, 1), (2, 54), (4, 77)) -> ((2, 54), (2, 70), (3, 1), (4, 77))
- 長方形を面積順に
- (2×100, 5×6, 10×8) -> (5×6, 10×8, 2×100)
- 文字列を辞書順に
- ("sort", "so", "algo", "study") -> ("algo", "so", "sort", "study")
実務で実際にソートアルゴリズムを用いる場面では、複雑なメンバ変数たちを抱えたオブジェクトについてソートすることも多いでしょう。そのような場面であっても、比較演算子「<」をオーバーロードしたものや、比較関数が定義できていれば、ソートを実行することができます。
2. ソートに要する計算時間
ソートアルゴリズムは、アルゴリズムの計算量オーダーを改善する過程を学ぶ題材として格好です。$n$ を並び替えたい要素数とします。
素朴な感性に基づくソートとしては
- 挿入ソート (かなり自然です)
- 選択ソート (貪欲法に基づいていて、とても自然です)
- バブルソート (それほど自然ではないかもしれません)
があります。これらは人間にとって自然なものですが、いずれも $O(n^2)$ の計算時間がかかります。しかし
- マージソート (分割統治法パラダイムを学べます)
- ヒープソート (ヒープはそれ自体が重要なデータ構造です)
といったより洗練されたアルゴリズムでは $O(n\log{n})$ の計算時間で終わらせることができます。このような $O$ 記法に不慣れな方向けに以下の記事も書きました:
ざっくりと言ってしまえば、
- $O(n)$ のアルゴリズムは、$n$ 回に比例した回数の計算ステップがかかる
- $O(n^2)$ のアルゴリズムは、$n^2$ 回に比例した回数の計算ステップがかかる
- $O(n\log{n})$ のアルゴリズムは、$n\log{n}$ 回に比例した回数の計算ステップがかかる
という感じです。
for (int i = 0; i < n; ++i) {
// なにかする
}
の形をしたアルゴリズムは $O(n)$ ですし、
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
}
}
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
}
}
の形をしたアルゴリズムはどちらも $O(n^2)$ になります。
このオーダー記法というものは慣れると物凄く使い勝手がよく、実装しようとしているアルゴリズムを実際に実装して実行しなくても、
どの程度の計算時間を要するかを予め大雑把に見積もることができる
ようになります!!!
もちろん $O(n^2)$ なアルゴリズムの正確な計算ステップ数が $\frac{1}{2} n^2$ 回で、$O(n)$ なアルゴリズムの正確なステップ数が $10n$ 回であることもあるわけですが、この $\frac{1}{2}$ や $10$ といった係数による差は微々たるもので、$n$ や $n^2$ といったオーダーの差が支配的であることがほとんどです。
さて、普通の PC では大体
$10^8$ 回のステップの計算に 1 秒かかる
という感じなのですが、それを踏まえて各オーダーのアルゴリズムが、入力サイズ $n$ に応じて計算ステップ数がどうなるかを大まかに整理してみます。1 秒以上かかる部分 (計算ステップ数が $10^8$ 回を超える部分) は 「-」 で記載しています。
| $\log{n}$ | $n$ | $n\log{n}$ | $n^2$ | $n^3$ | $2^n$ | $n!$ |
|---|---|---|---|---|---|---|
| 2 | 5 | 12 | 25 | 130 | 30 | 120 |
| 3 | 10 | 33 | 100 | 1,000 | 1,024 | 3,628,800 |
| 4 | 15 | 59 | 225 | 3.375 | 32,768 | - |
| 4 | 20 | 86 | 400 | 8,000 | 1,048,576 | - |
| 5 | 25 | 116 | 625 | 15,625 | - | - |
| 5 | 30 | 147 | 900 | 27,000 | - | - |
| 7 | 100 | 664 | 10,000 | 1,000,000 | - | - |
| 8 | 300 | 2,468 | 90,000 | 27,000,000 | - | - |
| 10 | 1,000 | 9,966 | 1,000,000 | - | - | - |
| 13 | 10,000 | 132,877 | 100,000,000 | - | - | - |
| 16 | 100,000 | 1,660,964 | - | - | - | - |
| 20 | 1,000,000 | 19,931,568 | - | - | - | - |
こうしてみると、$O(\log{n})$ はすごいですね。$n$ をいくら増やしてもビクともしません。それに比べて $O(n!)$ は一瞬で力尽きました。$O(2^n)$ も早々に力尽きてしまいました。$O(n^2)$ はそこそこ頑張りますがやはり $n$ が大きくなると厳しいです。$O(n\log{n})$ はかなり頑丈です。こうしてみると
- $O(n^2)$ のアルゴリズムでは $n \le 10,000$ くらいが限界
- $O(n\log{n})$ のアルゴリズムなら $n \le 1,000,000$ 程度ではまだ余裕
という圧倒的な差があることがわかります。本記事では「ソートの使いどころ」について見た後は、このようなオーダー改善を最短コースで体験するために、まずは
- 挿入ソート ($O(n^2)$)
- マージソート ($O(n\log{n})$)
に絞って見て行きたいと思います。その後で、クイックソート、ヒープソート、バケットソートについても見て行き、最後にその他の様々なソートを見て行きたいと思います。
3. ソートの使い方・使いどころ
3-1. ソートライブラリの使い方
現代のソート入門資料では欠かせない解説だと思います。各言語別に見て行きたいと思います。
C++
STL の <algorithm> をインクルードします。std::sort() が使えます。
# include <iostream>
# include <algorithm>
using namespace std;
int main() {
int N; // 要素数
int a[100000]; // 要素数 100000 以下とします
cin >> N;
for (int i = 0; i < N; ++i) cin >> a[i];
sort(a, a + N); // a[0:N] を小さい順にソート
// 出力
for (int i = 0; i < N; ++i) cout << a[i] << " ";
cout << endl;
}
入力として
8
12 66 3 23 51 89 15 37
を与えると出力結果として
3 12 15 23 37 51 66 89
が帰って来ます。上のソースコードでは配列でやっていましたが、std::vector についてもソートができます。
# include <iostream>
# include <algorithm>
# include <vector>
using namespace std;
int main() {
int N; // 要素数
vector<int> a;
cin >> N;
for (int i = 0; i < N; ++i) {
int a_temp;
cin >> a_temp;
a.push_back(a_temp);
}
sort(a.begin(), a.end()); // a を小さい順にソート
// 出力
for (int i = 0; i < N; ++i) cout << a[i] << " ";
cout << endl;
}
また、大きい順にソートしたいときは
# include <iostream>
# include <algorithm>
# include <vector>
using namespace std;
int main() {
int N; // 要素数
vector<int> a;
cin >> N;
for (int i = 0; i < N; ++i) {
int a_temp;
cin >> a_temp;
a.push_back(a_temp);
}
sort(a.begin(), a.end(), greater<int>()); // a を大きい順にソート
// 出力
for (int i = 0; i < N; ++i) cout << a[i] << " ";
cout << endl;
}
とすればよいですし、特殊な比較関数 (ここでは 50 と近い順でやってみます) で比較したいときは
# include <iostream>
# include <algorithm>
# include <vector>
using namespace std;
bool cmp(int a, int b) {
return abs(a - 50) < abs(b - 50);
}
int main() {
int N; // 要素数
vector<int> a;
cin >> N;
for (int i = 0; i < N; ++i) {
int a_temp;
cin >> a_temp;
a.push_back(a_temp);
}
sort(a.begin(), a.end(), cmp); // 50 と近い順にソート
// 出力
for (int i = 0; i < N; ++i) cout << a[i] << " ";
cout << endl;
}
とすればよいです。結果は
51 37 66 23 15 12 89 3
となりました。
Python
sorted を使うのが簡潔です
>>> sorted([12, 66, 3, 23, 51, 89, 15, 37])
[3, 12, 15, 23, 37, 51, 66, 89]
あるいは .sort() を用いてもよいでしょう
>>> a = [12, 66, 3, 23, 51, 89, 15, 37]
>>> a.sort()
>>> a
[3, 12, 15, 23, 37, 51, 66, 89]
その他の言語
その他の言語でのソートのやり方については、
の冒頭で「AtCoder に登録したら解くべき精選過去問 10 問を ◯◯◯ で解いてみた」シリーズをまとめたのですが、精選過去問 10 問のうちの 6 問目「ABC 088 B - Card Game for Two」がソートを用いる問題になっているので、各言語の 6 問目の解説を読むとよいです。
3-2. ソートアルゴリズムの使いどころ
ソートの使い道を挙げていきます。
大量の二分探索クエリの前処理として
配列の中から目的のものを探すのに、線形探索は $O(n)$ ですごく遅くて、二分探索なら $O(\log{n})$ で速いという話は、アルゴリズムを勉強するとしばしば耳にすることになります。二分探索ができるためには配列が予めソートされていることが必要なので、そこでソートの出番だというわけです。その辺りの話は
にも書いてあります。しかし疑問が浮かんだ方も多いと思います。
線形探索は遅いと言っても $O(n)$ でできる。
いくら二分探索が速いからと言って、予めソートするのに $O(n\log{n})$ かかるのでは意味がないのでは?
実際のところ「目的のものを探す」クエリが 1 回だけならばソートする意味はないです。しかし「目的のものを探す」クエリが大量に飛んで来るとなると話は大きく変わります。仮に配列サイズが $n$ で、 $Q$ 回のクエリが飛んで来るとすると
- 毎回線形探索では最悪 $O(Qn)$ の計算時間
- ソートしてから毎回二分探索なら最悪 $O(n\log{n} + Q\log{n})$ の計算時間
になります。$n = 100,000$, $Q = 100,000$ とすると
- 毎回線形探索: $10,000,000,000$ 回
- ソートして毎回二分探索: $3,321,928$ 回
という圧倒的な差が出ます。大規模データ解析の需要が高まっている昨今、このように様々なクエリを爆速に処理していくニーズはひたすらに高まっています。ソートはそのようなクエリの前処理として有効である場面はとても多いです。
特定のキーでデータを並び替えたりなど
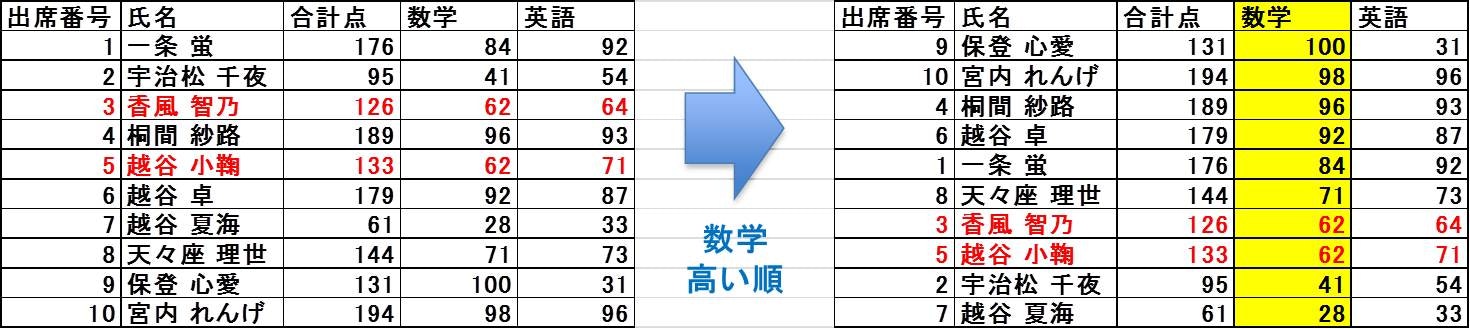
オーソドックスなソートの使い方です。
- 生徒の科目別成績表があって、科目ごとに得点順に並び替える
- データ分析の場面で特定のキーに沿ってデータを並び替える
など、多種多様な場面で使用されます。
このように特定のキーでデータを並び替える場面では「ソートの安定性」が重視されるときがあります。例えば上の例では、数学の得点が同点の香風智乃さんと越谷小鞠さんの順番はソートの前後で保たれていますが、このような性質を満たしたソートを安定ソートと呼びます。安定でないソートでは、この順番が入れ替わってしまう可能性があります。
しかし実は、安定でないソートを用いても以下のようにすれば問題を回避できます:
(数学の得点) をキーとする代わりに、(数学の得点, 生徒番号) のペアをキーとする
こうすることで、数学の得点が同点の生徒同士にもきちんとした「順序」がつけられます。現代では、このような少し複雑なキーによるソートも簡単にできるようになりました。
コンピュータグラフィックスや、タスクスケジューリングなど
コンピュータグラフィックス分野において、様々な物体を描画したり物体の相互干渉などを考えたりするとき、左や下(上)から順番に物体を処理していくことが多いが、このとき物体の位置関係をあらかじめソートしておくことでスムーズな処理が可能になります。類似の事情はタスクスケジューリングなどでも発生し、タスクをタスク発生時刻によってソートしておくことで、スムーズなスケジューリング処理が可能になることが多いです。
上位 k 個をとりたいとき
$n$ 個の整数 $a[0], a[1], \dots, a[n-1]$ が与えられたとき、その中の最小値を知りたい場面では、ソートするまでもなく線形探索すれば $O(n)$ で求めることができます。しかし小さい順に $k$ 個知りたいとなった場合にはソートの出番です。小さい順にソートして前から順に $k$ 個とればよいです。
小さい順に $k$ 個知りたい場面として代表的なものはビームサーチが挙げられます。ビームサーチは「あらゆるものを調べ尽くすことが不可能なほどに探索領域が広い」場面で、常に上位 $k$ 個の選択肢を確保しながら探索を進めていく方法なのですが、詳しく知りたい方は
を読んでいただければと思います。ビームサーチが有効に使われる場面として、最近大流行中のディープラーニングからの話題があります。自然言語処理の多くの分野でデファクトスタンダードとなった seq2seq 学習の推論時に decoder 部分でビームサーチを取り入れることが多く、単に貪欲法による推論を行うよりも精度が向上します。
数値計算時の情報落ちの影響を小さくする
数値積分はじめとした数値計算を行うとき、何個かの値を合計する処理をしばしば行います。そのときに怖いのは、絶対値の大きい値と絶対値の小さい値とを加算したときの「情報落ち」です。情報落ちを防ぐ対策の 1 つとして、合算する値を小さい順にソートして、その順に合計していくことが有効です。
様々な貪欲アルゴリズムの前処理として
広く知られている有名な貪欲アルゴリズムたちは、前処理としてソート処理を行うものが多いです:
- 全域最小木を求める Kruskal のアルゴリズム
- 前処理としてグラフの「辺」を重みが小さい順にソート
- 区間スケジューリング問題に対する貪欲解法
- 前処理として区間を終端時刻が早い順にソート
有名な貪欲アルゴリズムでなくても、貪欲法が有効な問題を解くときは、前処理としてのソートが有効なケースが多いです。
様々なアルゴリズムの前処理として
貪欲解法でなくても、前処理としてソートして順序を固定して考えることが有効なケースは多いです。よく言われる「二分探索」もその一例と言えます。その辺りの話は
が参考になります。
4. 挿入ソート: O(n^2)
それではいよいよ具体的なソートアルゴリズムに入っていきたいと思います。まずは素朴なソートから入って行きます。挿入ソートは、
- 前から順番に、i 番目の要素を適切な場所へ挿入することを繰り返す
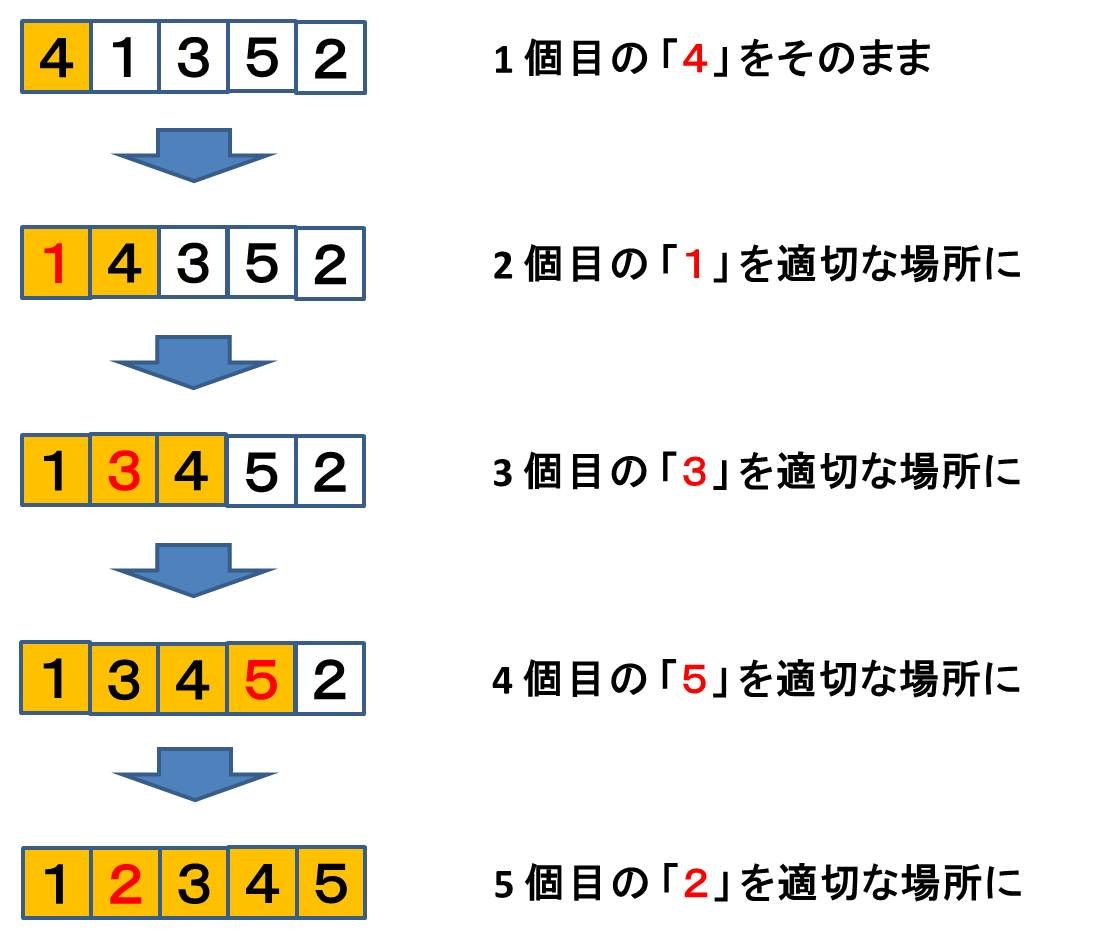
というアルゴリズムです。「41352」に対する動作例はこんな感じです。1 個目の「4」はそのままで、2 個目の「1」を適切な場所まで前に持っていきます。次に 3 個目の「3」を適切な場所まで前に持っていきます。次に 4 個目の「5」を適切な場所まで前に持っていきます (「5」はその手前の4より既に大きいので結局動きません)。最後に 5 個目の「2」を適切な場所まで前に持っていきます。
可視化動画「15 Sorting Algorithms in 6 Minutes」の 0:10 辺りから挿入ソートの可視化が載っていて、わかりやすいです。
これを C++ で実装すると以下のようになります:
# include <iostream>
# include <vector>
using namespace std;
int main() {
int n; // 要素数
cin >> n;
vector<int> a(n); // 整列したい配列ベクトル (サイズ を n に初期化)
for (int i = 0; i < n; ++i) {
cin >> a[i]; // 整列したい配列を取得
}
/* 挿入前の配列を出力してみる */
cout << "Before: ";
for (int i = 0; i < n; ++i) cout << a[i] << " ";
cout << endl;
/* 挿入ソート */
for (int i = 1; i < n; ++i) {
int v = a[i]; // 挿入したい値
// v を挿入する適切な場所 j を探す
int j = i;
for (; j > 0; --j) {
if (a[j-1] > v) { // v より大きいやつは 1 個後ろに移す
a[j] = a[j-1];
}
else break; // v 以下になったら止める
}
a[j] = v; // 最後に j 番目に v を挿入
/* 各ステップの配列を出力してみる */
cout << "After Step " << i << ": ";
for (int i = 0; i < n; ++i) cout << a[i] << " ";
cout << endl;
}
return 0;
}
標準入出力やデバッグ出力を含めているので少し長いコードになっています。これに以下の入力をしてみましょう:
5
4 1 3 5 2
そうすると出力は次のようになりました:
Before: 4 1 3 5 2
After Step 1: 1 4 3 5 2
After Step 2: 1 3 4 5 2
After Step 3: 1 3 4 5 2
After Step 4: 1 2 3 4 5
4-1. 挿入ソートの計算量
最悪ケースでは $O(n^2)$ かかります。具体的な最悪ケースは「54321」のようなケースです。毎回挿入すべき要素を先頭まで引っ張って行くので、そのときの移動回数は
$1 + 2 + ... + (n-1) = \frac{1}{2} n(n-1) = \frac{1}{2}n^2 - \frac{1}{2}n$
となり、これは $O(n^2)$ です。なお、$O(n^2)$ がいかに遅いかを実感するためには、サイズ $n = 10,000,000$ の入力を与えてみるとよいです。C++ の std::sort() なら 1 秒程度で終了しますが、挿入ソートでは 1 時間かかっても終わりません!
4-2. 挿入ソートの性質
内部ソート、安定ソートについては「9. ソートに関する追加 tips」のところで解説しています。
- 挿入ソートは内部ソート (外部メモリをほぼ必要としない) である (😄)
- 挿入ソートは安定ソート (同一キーの順序は保存) である (😄)
- 元々の数列がほとんど整列済みの場合は、高速に動作する (ほとんど swap する必要がないため)
このように挿入ソートは、$O(n^2)$ なソートアルゴリズムとしてはいい性質を備えています。他にメジャーな $O(n^2)$ なソートアルゴリズムとしては「選択ソート」「バブルソート」がありますが、多くの場合挿入ソートの方が高速に動作します。
また、ほとんど整列済みの数列 (具体的には、転倒数が $O(n)$ な数列) に対しては $O(n)$ で動作するという際立った特徴があり、場合によってはクイックソートよりも高速なことがあります。そのため C++ の std::sort() は基本的にはクイックソートをベースとしつつも、「配列全体がほとんど整列済みに近い状態になったら最後は挿入ソートを決める」など、挿入ソートも一部取り入れています。
参考資料:
5. マージソート: O(n log n)
さて、挿入ソートは素朴で安定なソートでしたが、$O(n^2)$ かかるものでした。これでは 1 秒以内にソートしようと思うと $n \le 10,000$ 程度までしか太刀打ちできません。これを $O(n\log{n})$ に改善します。そうすれば $n \le 10,000,000$ 程度までは 1 秒以内にソートできるようになります!
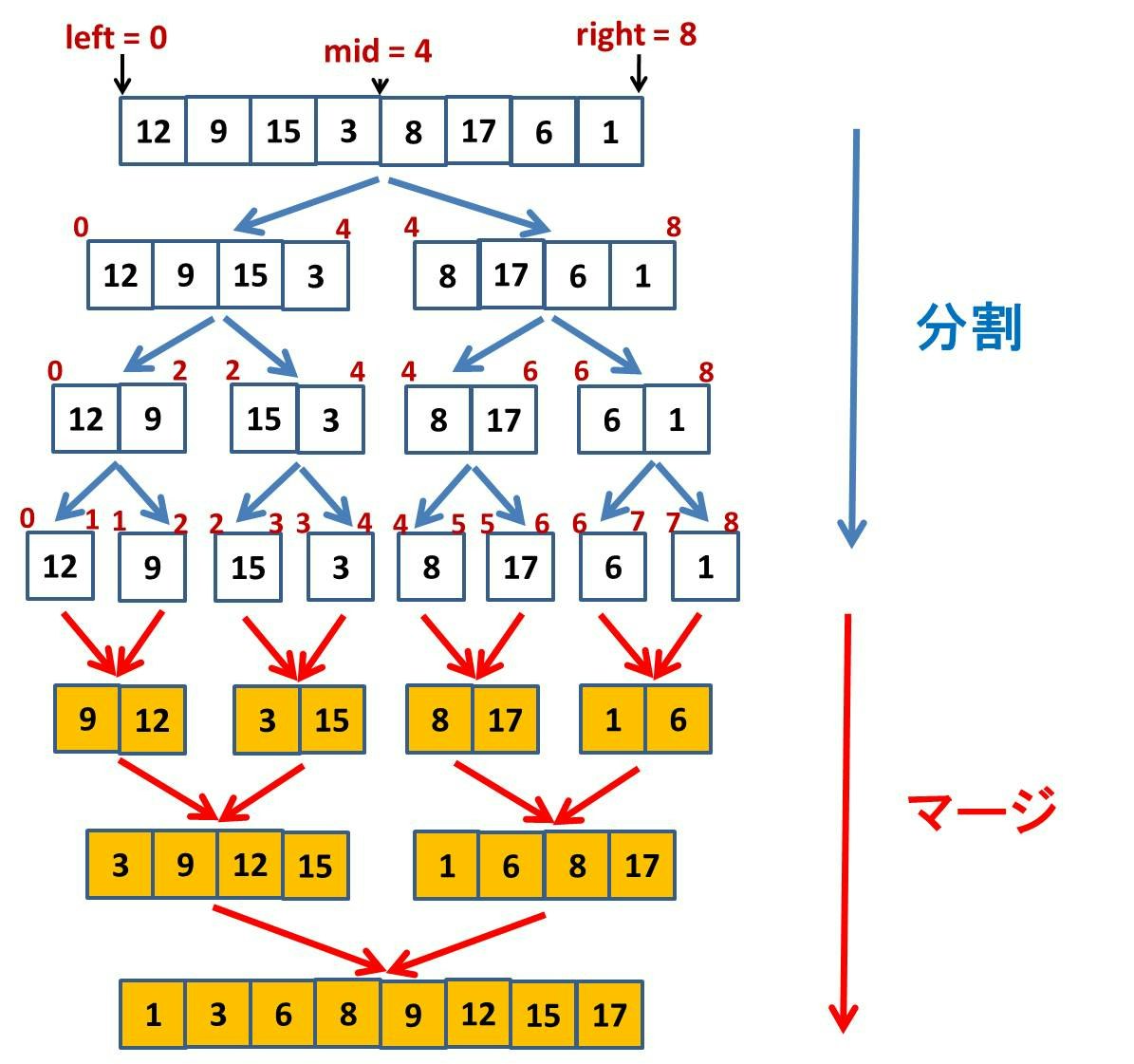
マージソートは、再帰を利用したソートアルゴリズムです。配列を半分に分けて、それぞれをソートしておいて、その 2 つをマージすることを繰り返します。MergeSort(a, left, mid) は配列の左半分をソートして、MergeSort(a, mid, right) は配列の右半分をソートします。そしてそれらをマージします。なお、マージソートの動きの直感的イメージについては可視化動画「15 Sorting Algorithms in 6 Minutes」の 1:06 の辺りを見るとよくわかります。
このように問題をいくつかの部分問題に分解して、それぞれ再帰的に解いて、マージしてまとめるアルゴリズム技法を分割統治法と呼びます。分割統治法については後日改めて特集記事を書きたいと思います。
MergeSort(a, left, right): 配列 a の left 〜 right 部分 a[left:right] をソートする
- right - left == 1 だったらリターンする (要素数 1 なので)
- mid = (left + right) / 2
- MergeSort(a, left, mid)
- MergeSort(a, mid, right)
- a[left:mid] と a[mid:right] をマージして、a[left:right] 全体をソート済み状態にする
という再帰関数を用意しておいて、
- MergeSort(a, 0, n)
を呼ぶ
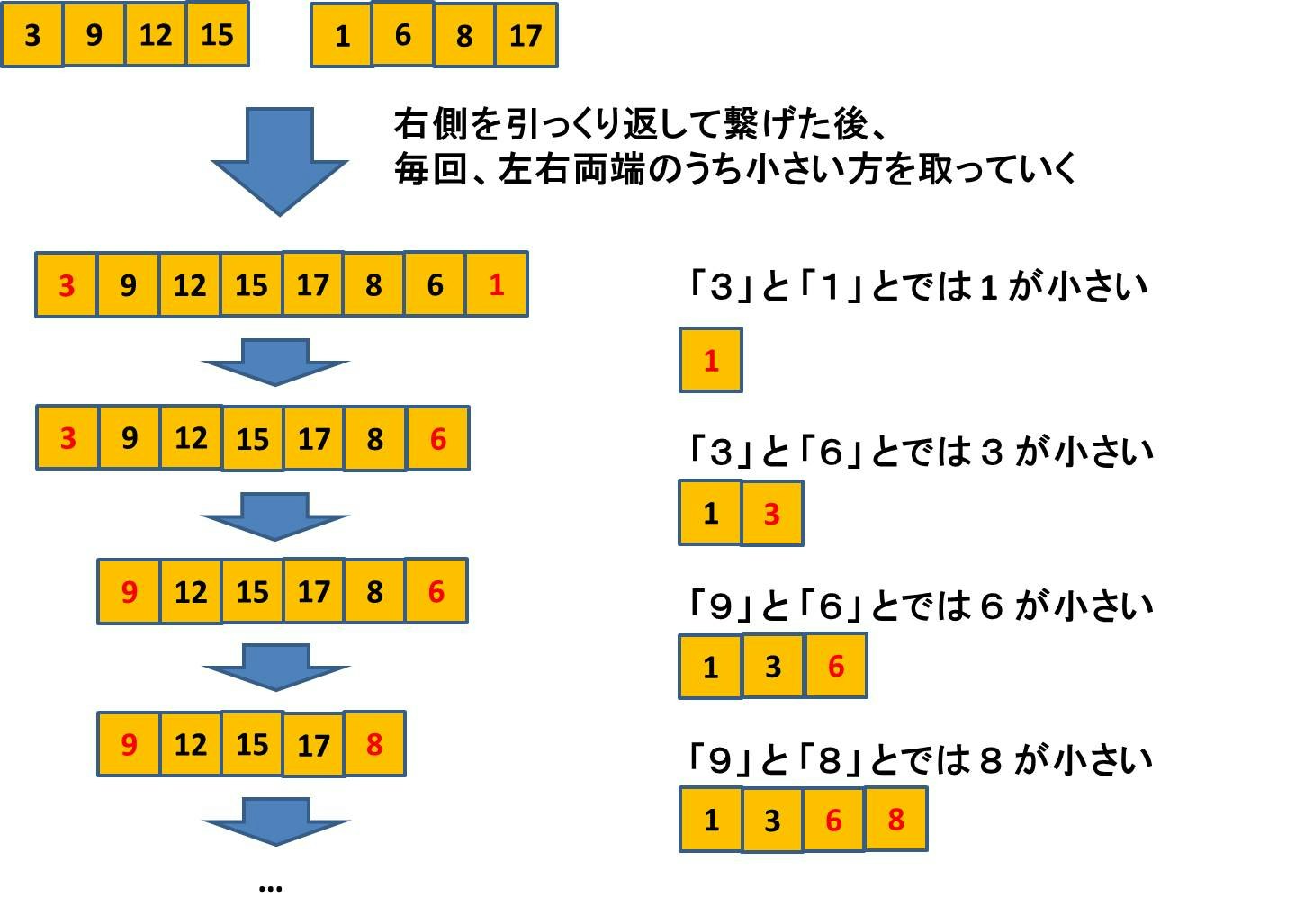
すごく複雑なことをやっているように見えてしまいますが、実際に頑張るのは「マージ」する部分になります。すなわち例えば下図のようなステップをどのように実装するかに尽きます。

ここをうまく実装できれば、再帰関数が全部よしなにしてくれます。マージ方法は図のようになります:
具体的な実装は以下のようになります。
# include <iostream>
# include <vector>
using namespace std;
/* 配列 a の [left, right) をソートします */
void MergeSort(vector<int> &a, int left, int right) {
if (right - left == 1) return;
int mid = left + (right - left) / 2;
// 左半分 [left, mid) をソート
MergeSort(a, left, mid);
// 右半分 [mid, right) をソート
MergeSort(a, mid, right);
// 一旦「左」と「右」のソート結果をコピーしておく (右側は左右反転)
vector<int> buf;
for (int i = left; i < mid; ++i) buf.push_back(a[i]);
for (int i = right-1; i >= mid; --i) buf.push_back(a[i]);
// マージする
int iterator_left = 0; // 左側のイテレータ
int iterator_right = (int)buf.size() - 1; // 右側のイテレータ
for (int i = left; i < right; ++i) {
// 左側採用
if (buf[iterator_left] <= buf[iterator_right]) {
a[i] = buf[iterator_left++];
}
// 右側採用
else {
a[i] = buf[iterator_right--];
}
}
}
int main() {
int n; // 要素数
cin >> n;
vector<int> a(n); // 整列したい配列ベクトル (サイズ を n に初期化)
for (int i = 0; i < n; ++i) {
cin >> a[i]; // 整列したい配列を取得
}
/* マージソート */
MergeSort(a, 0, n);
return 0;
}
5-1. マージソートの計算量
マージソートの計算量は最悪ケースでも $O(n\log{n})$ になります!!!
そのことを理解する方法は
- ざっくり図解する
- 計算量の漸化式をきっちり解く
といった方法があります。きちんと証明するには漸化式を解くのがよいですが、ここではざっくり図解することにします。漸化式を用いた計算量解析の議論については以下の記事を参考にしていただけたらと思います:
さて、マージソートの図を見ると、「分割」と「マージ」はそれぞれ $O(\log{n})$ ステップになることがわかります。というのも、1 回の分割で配列のサイズが半分になるので、配列サイズが 1 になるまでの分割回数は $O(\log{n})$ になります。そして 1 回のステップのマージ処理には $O(n)$ だけの計算時間がかかっていることがわかります。よってまとめると計算時間オーダーは $O(n\log{n})$ になります。
5-2. マージソートの性質
内部ソート、安定ソートについては「9. ソートに関する追加 tips」のところで解説しています。
- マージソートは外部ソート (外部メモリが必要) である (😩)
- マージソートは安定ソート (同一キーの順序は保存) である (😄)
マージソートは高速なソートでありながら安定ソートでもある特長があります。他に高速なソートとしては、クイックソート、ヒープソートがありますが、いずれも安定ソートではないです。しかしながらマージソートは、外部メモリ (上のソースコードでは baf) が必要で余分にメモリを食うことには注意が必要です。
...といったことが昔は言われていたのですが、マージソートはメモリを余分に食うとは言っても、元の入力配列の 2 倍のメモリ消費量程度で済みます。現代のメモリを潤沢に使える環境では、その程度のことは気にならないケースがほとんどです。なお、外部メモリをほとんど使わなくて済む in-place マージソートも研究されています。
マージソートはどんな入力ケースに対しても高速で、しかも安定ソートであることから、「マージソートちゃんマジソート」という標語もあり、実践的に用いるアルゴリズムの有力候補になります。ただしほとんどのケースに対してクイックソートの方が高速に動作するので、 C++ の std::sort() はクイックソートがベースになっています。
6. クイックソート: 乱択アルゴリズムのよい題材
クイックソートもマージソートと同様に、配列を分割して再帰的にソートする分割統治法アルゴリズムです。
マージソートは最悪時でも計算時間が $O(n\log{n})$ でおさまるのに対し、クイックソートは最悪時の計算時間が $O(n^2)$ かかります。それにもかかわらずクイックソートは「実用上は平均的に非常に高速」「外部メモリを必要としない内部ソートである」といった利点によりしばしば用いられます。
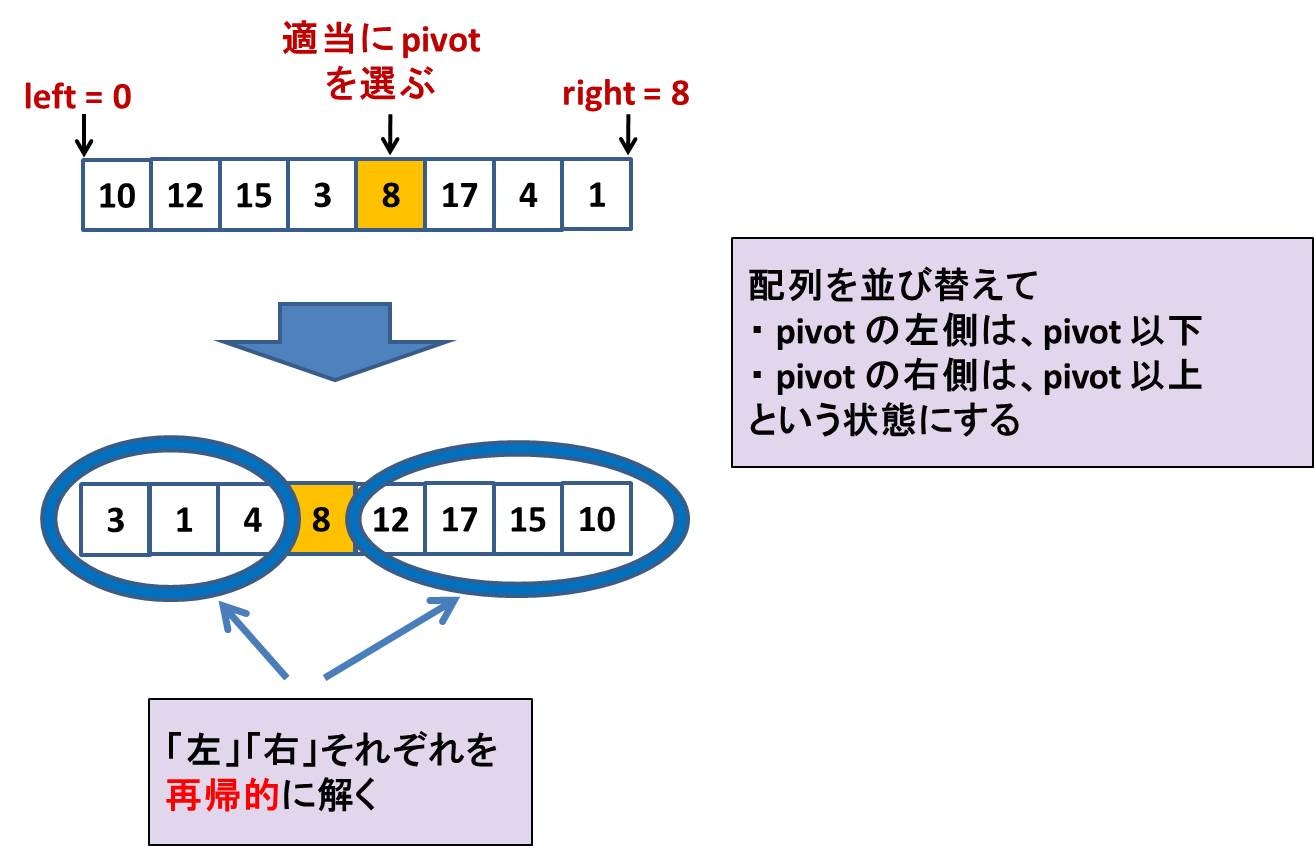
さて、クイックソートは以下のようなアルゴリズムです。配列の中から適当な要素 pivot を選び出し、配列全体を「pivot 未満のグループ」「pivot 以上のグループ」に分割して、それぞれを再帰的に解きます。ソート可視化動画「15 Sorting Algorithms in 6 Minutes」の 0:39 からクイックソートが可視化されていてわかりやすいです。
QuickSort(a, left, right): 配列 a の left 〜 right 部分 a[left:right] をソートする
- right - left == 1 だったらリターンする (要素数 1 なので)
- 配列 a[left:right] の要素を 1 つ選ぶ (pivot と呼ぶ)
- a[left:right] を適切に並び替えて、pivot より左側は pivot 未満、右側は pivot 以上になるようにする (このとき、pivot の来る index を i とする)
- QuickSort(a, left, i)
- QuickSort(a, i+1, right)
という再帰関数を用意しておいて、
- QuickSort(a, 0, n)
を呼ぶ
イメージを図にするとこのような感じです:
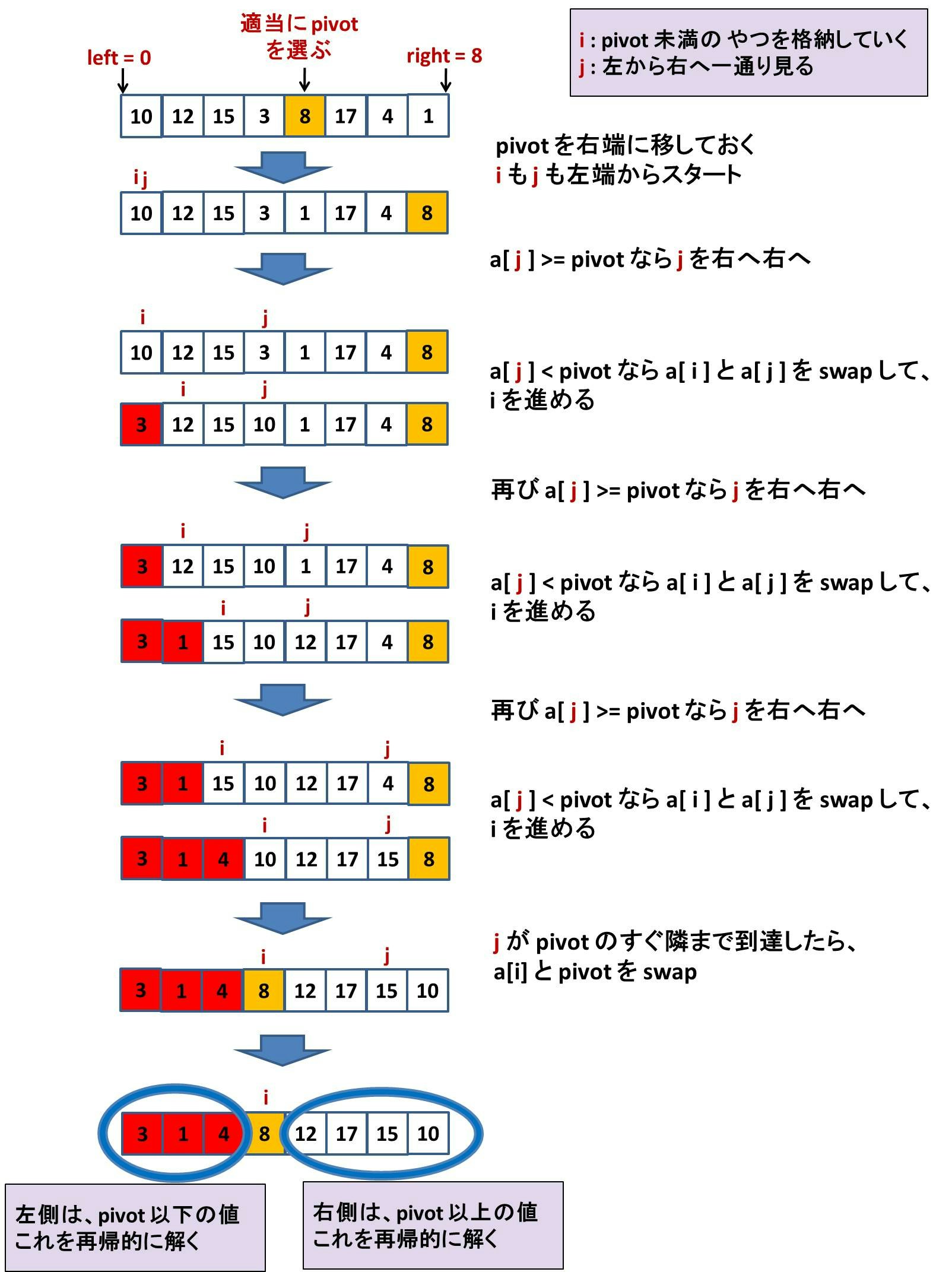
さて、当然難しいところは、配列を並び替えて「pivot の左側は pivot 未満、pivot の右側は pivot 以上」となるようにする部分です。これは以下のようにやります。少し技巧的に見えるかもしれません。
- j は配列を左から右へと一通り全部の値を見る
- そのうち pivot 未満だったやつを左詰めにしていく
という感じです。
以上の処理を C++ で実装すると以下のようになります:
# include <iostream>
# include <vector>
using namespace std;
/* 配列 a の [left, right) をソートします */
void QuickSort(vector<int> &a, int left, int right) {
if (right - left <= 1) return;
int pivot_index = (left + right) / 2; // 適当にここでは中点とします
int pivot = a[pivot_index];
swap(a[pivot_index], a[right - 1]); // pivot と右端を swap
int i = left; // iterator
for (int j = left; j < right - 1; ++j) { // j は全体を眺めて
if (a[j] < pivot) { // pivot 未満のがあったら左に詰めていく
swap(a[i++], a[j]);
}
}
swap(a[i], a[right - 1]); // pivot を適切な場所に挿入
/* 再帰的に解く */
QuickSort(a, left, i); // 左半分 (pivot 未満)
QuickSort(a, i + 1, right); // 右半分 (pivot 以上)
}
int main() {
int n; // 要素数
cin >> n;
vector<int> a(n); // 整列したい配列ベクトル (サイズ を n に初期化)
for (int i = 0; i < n; ++i) {
cin >> a[i]; // 整列したい配列を取得
}
/* クイックソート */
QuickSort(a, 0, n);
return 0;
}
6-1. クイックソートの計算量
クイックソートの計算量は、ピボットの選び方に依存します。
もし最大限に偏った非常に悪いピボットの選び方をすると計算時間は $O(n^2)$ になります。例えばピボットによる左右分割が、常に片方が 0 個でもう片方にすべて偏った場合には計算時間が $O(n^2)$ になります。
反対に常に分割が左右均等に分かれていれば、計算時間は $O(n\log{n})$ になります。そればかりか実は少々偏らせる程度では $O(n^2)$ にはならず、例えば分割が毎回 1:99 に分かれるとしても、1:99 で不変である限りは計算時間は $O(n\log{n})$ になります (ここはよく誤解されがちです)。
クイックソートの計算量は平均的には $O(n\log{n})$ になります。しかしそれが言えるためには
入力として与えられる配列の順序を表す順列は、$n!$ 通りのパターンが等確率で出現する
という重要な仮定が必要です。現実的には入力分布の偏りによって、そのような仮定が成立すると期待できない状況も多々考えられます。そこでクイックソートのピボット選択を乱択化する手法が考えられます。
6-2. クイックソートの乱択化
乱択アルゴリズムとは、「ランダムに選ぶ」という要素を含めたアルゴリズムのことです。アルゴリズムを乱択化することには多彩な役割があるのですが、以下のスライドに非常によくまとまっています:
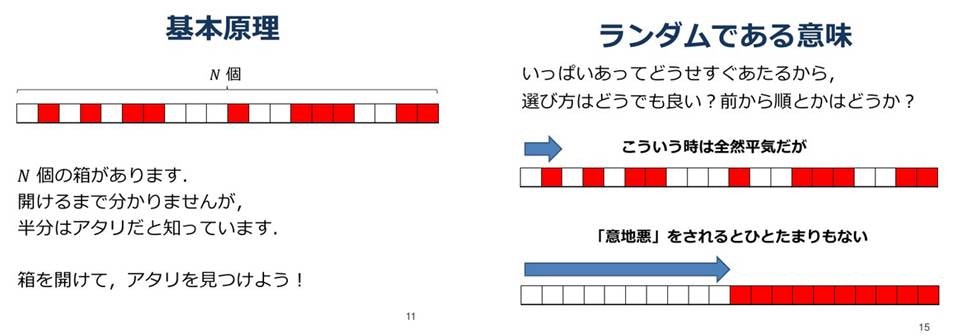
- プログラミングコンテストでの乱択アルゴリズム (下図はスライドからの引用)
スライドにもあるように、アルゴリズムを乱択化することは「意地悪なケース」や「入力が偏っているケース」への対策として有効です。クイックソートの例で言えば、配列の中からピボットを選択する部分を乱択化することが有効です。乱択化したクイックソートの平均計算量は $O(n\log{n})$ になります。そのことの詳しい解析は
- アルゴリズムイントロダクション の「7.4 クイックソートの解析」
- 数学ガール 乱択アルゴリズム の「第10章 乱択アルゴリズム」
に載っているので参考にしていただけたらと思います。
6-3. クイックソートの性質
内部ソート、安定ソートについては「9. ソートに関する追加 tips」のところで解説しています。
- クイックソートは内部ソート (外部メモリを必要としない) である (😄)
- クイックソートは安定ソート (同一キーの順序は保存) でない (😩)
マージソートと真逆ですね。クイックソートは実用上高速で、しかも内部ソートであることが、古くから盛んに用いられる要因になりました。C++ の std::sort() もクイックソートがベースになっていて、最悪時の計算時間の悪化に対応するために次章のヒープソートを取り入れたり (イントロソートとよびます)、少しでも高速にするために挿入ソートも取り入れたりしているようです。その結果、特に C++11 以降の std::sort() は最悪時の計算時間も $O(n\log{n})$ になることが保証されていて、実際上もナイーブなクイックソートと比べるとかなり高速に動作します。
- 参考: STLのsortの計算量
7. ヒープソート: オンラインクエリについて
ヒープソートもマージソートと同様、最悪時でも計算時間が $O(n\log{n})$ になります。
外部メモリを必要としない In-place ソートであるという嬉しい特長がありつつも、平均的な速度ではクイックソートに劣り、省メモリ性が必要な場面でもクイックソートでよくて、安定性が必要なときはマージソートを使いたくなるため、実用上の活躍の場はあまり無いソートアルゴリズムでもあります。
しかしながら、ヒープはそれ自体重要なデータ構造であり、ヒープを学ぶ意味は大いにあると言えます。またヒープソートは「与えられた配列をただ一度ソートするアルゴリズム」というよりは、配列の中身が変わったり、配列に新たな要素を追加したり、要素を削除したりすることが想定される場面で「最小値を常に取り出せるようにするアルゴリズム」だという側面も強いです。
7-1. ヒープとは
以下のような二分木 (またはそれを配列で表現したもの) をヒープと呼びます:
- 親ノードの値は子ノードの値以上である (図で言えば、例えばノード 2 はノード 5 の親ですが、ノード 2 の値は 15 で、ノード 5 の値 6 より大きいです)
- 木のノード番号が一番大きいノードより若い番号のノードはすべてある (図で言えば、ノード 11 があったらノード 0~10 はあります)

ヒープは配列を用いて簡単に実装することができます。単純にノード番号順に並べるだけでよいです。配列にするときに、親と子の関係を表現できる必要があるのですが
- ノード $k$ の子供は、$2k+1, 2k+2$ である
- ノード $k$ の親は、$(k-1)/2$ である (余りは切り捨て)
という関係が見て取れます。実際、例えばノード 2 の子供は、22 + 1 = 5 と、 22 + 2 = 6 になっています。逆にノード 5 の親は (5-1)/2 = 2 になっていますし、ノード 6 の親も (6-1)/2 = 2 (余り切り捨て) になっています。

7-2. ヒープができること
ヒープは以下のクエリを高速に処理することができます。特に「最大値の削除」を $O(\log{n})$ でできるのは優秀で、もし単なる配列でこれを実現しようと思ったら $O(n)$ かかります。削除した分の隙間を詰めないといけないためです。
| 処理内容 | 計算時間 | 備考 |
|---|---|---|
| 配列に値 $v$ を追加 | $O(\log{n})$ | 追加してもヒープ状態を保ちます |
| 配列内の最大値を知る | $O(1)$ | 二分木のルート (ノード 0) の値です |
| 配列から最大値を削除 | $O(\log{n})$ | ルートを消して木を整えます |
ヒープに値 v を追加
さきほどのヒープに値 17 を挿入しようとしてみましょう。とりあえず、17 をヒープの最後尾に加えてみます。しかし、図に示す通り、親ノードの方が本来値が大きくなるべきなのに逆転してしまっています!

そこで、逆転している部分を swap することで逆転関係を解消します。これにより、ノード 5 とノード 12 との親子関係がスッキリしました。注意点として、これによって元々良好だった「ノード 5 とノード 11 との親子関係」が壊れることはないです。なぜなら、ノード 11 にしてみれば、元の親よりもさらに大きな値が来ることになるからです。

しかし今度は、ノード 2 とノード 5 との親子関係がぎくしゃくしてしまいました。ですのでやはり値を swap します。そうすると今度はノード 0 とノード 2 の親子関係はしっくり来ているので、ヒープ全体としてちゃんと平和が保たれた状態になりました!

このように、ヒープに新たな値 $v$ を追加するときは、
- とりあえず最後尾にくっつける
- 親との関係が OK になるまで上へ上へと swap していく (最悪でもルートまで行って止まる)
という風にします。二分木の高さは $O(\log{n})$ なので、計算量は最悪時でも $O(\log{n})$ になります。
ヒープの最大値を知る
単にルートの値を見るだけでよいです。上図の例で言えば、ルートの値は 19 でそれが最大です。
ヒープから最大値を削除する
これができるのが強みです。

まずとりあえずはルートを削除してしまいます。これではヒープが崩壊してしまうので、とりあえず最後尾にあるノードを抜擢してルートに引っ張り上げます。

そうするともちろん親子関係が崩れてしまうので先程と同じように swap を繰り返して調整します。まず、抜擢したルートから見て左右の子供のうち、大きい方と swap します。なぜなら小さい方と swap してしまうと、その小さい子供が大きい子供の親になってしまって良くないからです。

あとはこれを均衡が保たれるようになるまで繰り返します。

計算時間は、最悪ケースではルートから一番下まで行くので $O(\log{n})$ になります。
7-3. ヒープの実装例
以上の心得があればヒープは簡単に実装できます。なお、C++ には既にヒープの実装があり、std::priority_queue を用いることができます。
# include <iostream>
# include <vector>
using namespace std;
struct Heap {
vector<int> heap;
Heap() {}
/* ヒープに値 v を挿入 */
void push(int v) {
heap.push_back(v); // 最後尾に値追加
int i = (int)heap.size() - 1; // 追加されたノード番号
while (i > 0) {
int p = (i - 1) / 2; // 親のノード番号
if (heap[p] >= v) break; // 逆転なかったら終わり
heap[i] = heap[p]; // 自分のノードを親の値に
i = p; // 自分は上に行く
}
heap[i] = v; // v は最終的にはこの位置に
}
/* 最大値を知る */
int top() {
if (!heap.empty()) return heap[0];
else return -1;
}
/* 最大値を削除 */
void pop() {
if (heap.empty()) return;
int v = heap.back(); // ノードに持ってくる値
heap.pop_back();
int i = 0; // 根から降ろしていく
while (i * 2 + 1 < (int)heap.size()) {
// 子供同士を比較して大きい方を child1 とする
int child1 = i * 2 + 1, child2 = i * 2 + 2;
if (child2 < (int)heap.size() && heap[child2] > heap[child1]) child1 = child2;
if (heap[child1] <= v) break; // 逆転なかったら終わり
heap[i] = heap[child1]; // 自分のノードを子供の値に
i = child1; // 自分は下に行く
}
heap[i] = v; // v は最終的にはこの位置に
}
};
7-4. ヒープソートの計算量と性質
このようなヒープがあればヒープソートは簡単に実現できることがわかるかと思います。
- サイズ $n$ の配列 $a[0:n]$ の要素をすべてヒープに挿入する ($O(\log{n})$ × $n$ 回)
- ヒープの最大値を順に pop して配列の後ろから詰めていく ($O(\log{n})$ × $n$ 回)
いずれのフェーズも $O(n\log{n})$ で実現できるので全体としての計算量も $O(n\log{n})$ になります。
ヒープソートは明らかに安定ソートではないです。なお、ヒープソートは一見「ヒープ」という外部メモリが必要そうに見えてしまうのですが、次節で見るように実は入力配列 $a$ そのものをヒープにしてしまうことによって、In-place な実装をすることができます。したがって
- ヒープソートは内部ソートである (😄)
- ヒープソートは安定ソートではない (😩)
という感じになります。
7-5. ヒープソートの in-place な実装
ソートしたい配列 a そのものをヒープにして以下のような実装ができます。
# include <iostream>
# include <vector>
using namespace std;
/* a のうち n 番目までをヒープとして、i 番目のノードについて下と比べて逆転していたら解消する */
void Heapify(vector<int> &a, int i, int n) {
int child1 = i * 2 + 1; // 左の子供
if (child1 >= n) return; // 子供がないときは終了
if (child1 + 1 < n && a[child1 + 1] > a[child1]) ++child1; // 子供同士を比較
if (a[child1] <= a[i]) return; // 逆転がなかったら OK
swap(a[i], a[child1]); // swap
/* 再帰的に */
Heapify(a, child1, n);
}
void HeapSort(vector<int> &a) {
int n = (int)a.size();
/* a 全体をヒープにするフェーズ */
for (int i = n / 2 - 1; i >= 0; --i) {
Heapify(a, i, n);
}
/* ヒープから 1 個 1 個最大値を pop するフェーズ */
for (int i = n - 1; i > 0; --i) {
swap(a[0], a[i]); // ヒープの最大値を左詰め
Heapify(a, 0, i); // ヒープサイズは i に
}
}
int main() {
int n; // 要素数
cin >> n;
vector<int> a(n); // 整列したい配列ベクトル (サイズ を n に初期化)
for (int i = 0; i < n; ++i) {
cin >> a[i]; // 整列したい配列を取得
}
/* ヒープソート */
HeapSort(a);
return 0;
}
7-6. より高度なオンラインクエリについて
ヒープソートはソートアルゴリズムというよりは、ヒープそのものの重要性を学ぶアルゴリズムという印象です。ヒープの特徴は
- 値 v を高速に挿入できる
- 最大値が常にわかる
- 最大値を高速に削除できる
というものでした。しかし実用上はより高度な機能が欲しくなるときもあります。具体的には「最大値が常にわかる」だけでなく、「小さい順に k 番目の値も常にわかる」ようなものが欲しいときもあります。もし
- 値 v を挿入できる
- 小さい順に k 番目の値がわかる
- 配列内に値 v があるかどうかを検索できる (さらに v が配列内で何番目に小さな値なのかも知る)
- 値 v を削除できる
という操作をすべて高速に行うことができたならば、いわばオンラインソートが高速にできているということができるでしょう。そのような処理を状況に応じて実現できるデータ構造を以下の記事に特集しましたので、興味のある方は参考にしていただけたらと思います:
8. 計数ソート: バケットは重要なデータ構造
計数ソートはバケットを用いるもので、単純な場合にはビンソート、バケットソートなどとも呼ばれます。これまでに見て来た挿入ソート、マージソート、クイックソート、ヒープソートとは毛色が異なるものです。
これまでのソートアルゴリズムは「大小比較」を元にしていました。ソートする配列の中身が数値だろうと、図形だろうと、文字列だろうと、大小比較ができるならばなんでもよいという圧倒的な汎用性がありました。一般に比較に基づくソートアルゴリズムは、今後どんなものを開発したとしても
任意の比較に基づくソートアルゴリズムは最悪時には $O(n\log{n})$ 回の比較が必要である
ことが示されています。証明はそれほど難しくはないです。「比較」に基づくソートアルゴリズムは「a > b ならばこうする、a <= b ならばこうする」といったように二分決定木を形作るものと考えることができます。ソートによって得られる最終状態は $n!$ 通りありうるので、二分決定木が $n!$ 個のリーフを持つ必要がありますが、そのために必要な二分決定木の高さ $h$ は、
$2^h \ge n!$
よって
$h \ge O(n\log{n})$ (Stirling の公式を用います)
が成り立ち、最悪時には $O(n\log{n})$ 回の比較が必要であることが言えます。このことから特に、マージソートとヒープソートはともに漸近的に最適な比較ソートであることが言えます。
ところが、計数ソートは一見すると $O(n)$ にできてしまうように見えます。そんな計数ソートを紹介します。
8-1. 計数ソート
ソートしたい配列 $a$ の各要素のキー値が $1$ から $A$ までの整数だったとします。そのとき、以下のような集計処理を行います。このような num 配列はしばしばバケットと呼ばれます。
num[i] := 配列 $a$ の中に数値 i が何個あったか
これは配列全体を for 文を舐めれば簡単にできます。そしてこの集計処理を行ったらソートを復元するのは簡単です:
# include <iostream>
# include <vector>
using namespace std;
const int MAX = 100000; // 配列の値は 100000 未満だとします
int main() {
int n; // 要素数
cin >> n;
vector<int> a(n); // 整列したい配列ベクトル (サイズ を n に初期化)
for (int i = 0; i < n; ++i) {
cin >> a[i]; // 整列したい配列を取得
}
/* 各要素の個数をカウントします */
/* num[v] := v の個数 */
int num[MAX] = {0};
for (int i = 0; i < n; ++i) {
++num[a[i]]; // a[i] をカウントします
}
/* num の累積和をとります */
/* sum[v] := v 以下の値の個数 */
int sum[MAX] = {0};
for (int v = 1; v < MAX; ++v) {
sum[v] = sum[v-1] + num[v];
}
/* sum を元にソート */
/* sorted: a をソートしたもの */
vector<int> sorted(n);
for (int i = n-1; i >= 0; --i) {
sorted[--sum[a[i]]] = a[i];
}
return 0;
}
注意点として、ソートしたい要素のキーが「$1$ から $A$ までの整数」であるばかりでなく、ソートしたい要素自体がただの「$1$ から $A$ までの整数」だった場合には下のような直感的な簡潔な実装も可能です:
# include <iostream>
# include <vector>
using namespace std;
const int MAX = 100000; // 配列の値は 100000 未満だとします
int main() {
int n; // 要素数
cin >> n;
vector<int> a(n); // 整列したい配列ベクトル (サイズ を n に初期化)
for (int i = 0; i < n; ++i) {
cin >> a[i]; // 整列したい配列を取得
}
/* 各要素の個数をカウントします */
/* num[v] := v の個数 */
int num[MAX] = {0};
for (int i = 0; i < n; ++i) {
++num[a[i]]; // a[i] をカウントします
}
/* ソート済み配列 */
vector<int> sorted;
for (int v = 1; v < MAX; ++v) { // 各キー値 v に対して
for (int i = 0; i < num[v]; ++i) { // その個数分並べる
sorted.push_back(v);
}
}
return 0;
}
最初の累積和 sum を用いた実装では、ソートしたい配列の各要素が複雑なオブジェクトのインスタンスであった場合 (キー値は $1$ から $A$ までの整数) にも対応できるものになっています。また、これは計数ソートを基数ソートへと発展させる際に重要なことですが、計数ソートは安定ソートになっています。
8-2. 計数ソートの計算量
計数ソートの計算量は $O(n + A)$ になります。計数ソートはそもそも $A = O(n)$ である場合に使われることを考えると $O(n)$ であると言えます。
マージソートやヒープソートが $O(n\log{n})$ であったことに比べると夢のように思える計算量ですが、適用場面はキー値が $1$ から $A$ までの整数値であり、しかも $A$ が $A = O(n)$ 程度の小ささである場合に限られます。それでも例えば {$1, 2, ..., n$} の順列が与えられてそれを並び替えたいという場面は実用上も度々出現しますので、そのような場面ではクイックソートをも圧倒する無類の強さを誇ります。
8-3. 基数ソート (Radix Sort)
計数ソートをさらに発展させたもので、いわゆる「整数」など、位取り記数法で表現可能な対象をソートするアルゴリズムです。計数ソートは
num[i] := 配列 $a$ の中に数値 i が何個あったか
というバケットを用いたソートアルゴリズムでしたが、これでは配列中の数値が巨大になると厳しいです。そこで基数ソートの出番で、例えば配列中の数値が 7 桁以内であることがわかっていたら
- まず 1 の位について計数ソートする
- 次に 10 の位について計数ソートする
- 次に 100 の位について計数ソートする
- …
- 最後に 1,000,000 の位について計数ソートする
という風にやればよいです。直観的には 1,000,000 の位から順にソートしたくなるのですが、それだと各桁について再帰的にソートしていくことになるので、各桁についてソートする度に新たなバケットを用意するか、既に使っているバケットの中身を一旦他の場所で管理したりしなければならないコストが生じます。1 の位から順にソートするのであれば、次の桁へと移るたびに大小関係の優先度が上昇していくので、他の桁のことを気にせず猪突猛進にソートしていくことができます。ただし、各桁ごとのソートが安定ソートである必要があります。計数ソートは安定ソートなので要件を満たしています。
基数ソートの動きは可視化動画「15 Sorting Algorithms in 6 Minutes」の 1:55 からあります。ソートしたいキー値が整数だとわかっていれば非常に高速です。計算時間は $O(nk)$ ($k$ は最大桁数) になります。
8-4. バケットの考え方
計数ソート・基数ソートに限らず、バケットは非常に重要な概念です。バケットやそれに類するデータ構造を用いて実現できるアルゴリズムは数多く、Binary Indexed Tree を用いて転倒数を数え上げたり、k 番目の要素を求めたりする話題は、まさにバケット法の典型的な有効活用例と言えます。
また、基数ソートと類似の発想を用いるデータ構造として Radix Heap というものがあります。実際上高速なヒープで、最短経路を求めるダイクストラ法の高速化にも使えます。
- 参考: 色々なダイクストラ高速化 (yosupo さん)
9. ソートに関する追加 tips
ここから先は、
- ソートマニアになりたい
- 大学の講義の試験や応用情報試験などの対策として様々なソートを学ぶ必要がある
という方向けにソートに関する追加トピックを整理していきます。
9-1. 内部ソートと外部ソート
ソートに限らず、アルゴリズムの良さを示すものの 1 つに in-place 性と呼ばれるものがあります。これはアルゴリズムが入力を受け取った後に追加のメモリを (ほとんど) 使用しないものを指します。
ソートで言えば、
- 並び替えたい対象のサイズ $n$
- 並び替えたい対象の配列 $a[0:n]$
の分のメモリは入力を受け取るためにそもそも必要ですが、ソート処理の多くを配列 a 上の swap 操作で済ませることができるものを指します。そしてソートを終えた時には、出力データが入力データを上書きする形になります。In-place なソートを内部ソート、そうでないソートを外部ソートを呼びます。
メモリ使用量に厳しい制限のあった時代は「ソートアルゴリズムを内部ソートにできるか」というのは重要な問題意識でした。現代では特別に意識する必要のある場面は限られていますし、むしろ
- バグを埋め込みにくい実装をするのがよい
という観点からは、In-place 性を極端に追求する必要性は薄くなっていると言えるでしょう。組込系などの一部のメモリ使用量制限の厳しい状況下では重要な概念になります。
9-2. 安定なソートとは
ソートアルゴリズムの良さを示すものとして、安定性も挙げられます。安定なソートとは
同じキーをもつ要素間の順序関係が保たれる
ものを指します。つまり、5 つの要素
(3, A), (2, B), (6, C), (3, D), (1, E)
を数値をキーとして並び替えるときに
(1, E), (2, B), (3, D), (3, A), (6, C)
となってしまうのならば、それは安定なソートとは呼べないです。例えばクイックソートは安定性の保証はできないですが、マージソートは安定性の保証ができます。
ソートの安定性もメモリ使用制限の厳しい環境では重要な概念かもしれないですが、オブジェクト志向的なプログラミングが簡単にできるようになった現代では重要性が薄れています。それは、安定でないソートであっても、以下のようにして簡単に安定なソートにすることができるからです:
a[0], a[1], ..., a[N-1] を並び替えたいとき、代わりに
(a[0], 0), (a[1], 1), ..., (a[N-1], N-1) を辞書順に並び替える
この解決法は、単に「安定でないソートを安定にする」だけでなく、
- k 番目に大きい要素の id はなんであったか
を取り出すこともできるようになります。むしろその用途で使用することが多いテクニックです。
もちろん追加のメモリ容量を必要とするため、メモリ容量制限が厳しい環境では使えないテクニックですが、現代では一部の組込系を除いて、そのような場面は限られているでしょう。
10. その他のソート
ここまでに登場したソート以外の様々なソートを紹介します。
10-1. 選択ソート
選択ソートはそこそこメジャーなソートです。大学の授業などでも教えていることが多いと思いますし、恐らく最初に習うソートアルゴリズムでもあります。発想はとても自然で、貪欲法に基づいています。
- 配列の中から「残っているもののうち一番小さいものを前に持って来る」を繰り返す
というアルゴリズムです。選択ソートは計算量オーダーは $O(n^2)$ と効率が悪いです。内部ソートですが、安定ソートではありません。発想が自然なだけに色々と惜しい感じのソートですが、ヒープソートは選択ソートの思想を効率化して $O(n\log{n})$ に改良したものだと言えるでしょう。選択ソートの動きの直感的イメージについては可視化動画「15 Sorting Algorithms in 6 Minutes」の 0:00 からを見るとよくわかります。
# include <iostream>
# include <vector>
using namespace std;
void SelectionSort(vector<int> &a) {
for (int i = 0; i < (int)a.size(); ++i) {
int min_index = i; // i 番目以降で一番小さい値を探す
for (int j = min_index; j < (int)a.size(); ++j) {
if (a[j] < a[min_index]) {
min_index = j; // より小さいのがあったら更新
}
}
// 交換
swap(a[i], a[min_index]);
}
}
int main() {
int n; // 要素数
cin >> n;
vector<int> a(n); // 整列したい配列ベクトル (サイズ を n に初期化)
for (int i = 0; i < n; ++i) {
cin >> a[i]; // 整列したい配列を取得
}
/* 選択ソート */
SelectionSort(a);
return 0;
}
10-2. バブルソート
バブルソートも比較的メジャーなソートで、やはり大学の授業などで教えていることも多いと思われます。発想はそこそこ自然で、
- 配列の中から「大きさが逆転している部分があったら swap する」を繰り返す
というアルゴリズムです。バブルソートは計算量オーダーは $O(n^2)$ と効率が悪いです。内部ソートであり、安定ソートでもあります。しかし $O(n^2)$ な効率悪い初等ソートアルゴリズムの中でも大分遅い方です。バブルソートの動きの直感的イメージについては可視化動画「15 Sorting Algorithms in 6 Minutes」の 4:00 からを見るとよくわかります (下の実装とは左右の動きの向きは逆です)。
# include <iostream>
# include <vector>
using namespace std;
void BubbleSort(vector<int> &a) {
for (int i = 0; i < (int)a.size() - 1; ++i) {
for (int j = (int)a.size() - 1; j > i; --j) {
if (a[j - 1] > a[j]) { // 大きさが逆転している箇所があったら swap
swap(a[j - 1], a[j]);
}
}
}
}
int main() {
int n; // 要素数
cin >> n;
vector<int> a(n); // 整列したい配列ベクトル (サイズ を n に初期化)
for (int i = 0; i < n; ++i) {
cin >> a[i]; // 整列したい配列を取得
}
/* バブルソート */
BubbleSort(a);
return 0;
}
10-3. シェーカーソート
シェーカーソートは大分マイナーです。大学の授業でも教えているところは少数でしょう。バブルソートのスキャンを双方向にして少し改良したソートで計算時間オーダーは $O(n^2)$ です。バブルソートの、わざわざ整列されているところも愚直にスキャンしていくような無駄な部分を少し省いた感じです。この改良により、挿入ソートと同様「ほとんど整列済みの入力データ」に対しては割と高速に動作します。内部ソートでもあり、安定ソートでもあります。可視化動画「15 Sorting Algorithms in 6 Minutes」の 4:19 からシェーカーソートです。
# include <iostream>
# include <vector>
using namespace std;
void ShakerSort(vector<int> &a) {
/* [left_ubdex, right_index] がスキャン範囲 */
int left = 0;
int right = (int)a.size() - 1;
while (true) {
/* 順方向スキャン */
int last_swap = left; // 最後に swap した index
for (int i = left; i < right; ++i) {
if (a[i] > a[i + 1]) {
swap(a[i], a[i + 1]);
last_swap = i;
}
}
right = last_swap; // スキャン範囲を狭める
if (left >= right) break; // スキャン範囲がなくなったら break
/* 逆方向スキャン */
last_swap = right ;// 最後に swap した index
for (int i = right; i > left; --i) {
if (a[i] < a[i - 1]) {
swap(a[i], a[i - 1]);
last_swap = i;
}
}
left = last_swap; // スキャン範囲を狭める
if (left >= right) break; // スキャン範囲がなくなったら break
}
}
int main() {
int n; // 要素数
cin >> n;
vector<int> a(n); // 整列したい配列ベクトル (サイズ を n に初期化)
for (int i = 0; i < n; ++i) {
cin >> a[i]; // 整列したい配列を取得
}
/* シェーカーソート */
ShakerSort(a);
return 0;
}
10-4. ノームソート
ノームソートもかなりマイナーです。大学の授業でも教えているところは少数でしょう。挿入ソートとよく似ていますが、挿入する部分をバブルソートっぽくやったソートで計算時間オーダーは $O(n^2)$ です。やはり挿入ソートと同様「ほとんど整列済みの入力データ」に対しては割と高速に動作し、その他の入力データに対しても挿入ソートと同等の性能を持っています。内部ソートでもあり、安定ソートでもあります。可視化動画「15 Sorting Algorithms in 6 Minutes」の 4:34 からノームソートです。
# include <iostream>
# include <vector>
using namespace std;
void GnomeSort(vector<int> &a) {
int g = 1;
while (g < (int)a.size()) {
if (a[g - 1] <= a[g]) ++g; // 逆転していないので 1 個進む
else {
swap(a[g - 1], a[g]); // 逆転しているところは swap
if (g > 1) --g; // 左端にならない限り 1 個戻る
}
}
}
int main() {
int n; // 要素数
cin >> n;
vector<int> a(n); // 整列したい配列ベクトル (サイズ を n に初期化)
for (int i = 0; i < n; ++i) {
cin >> a[i]; // 整列したい配列を取得
}
/* ノームソート */
GnomeSort(a);
return 0;
}
10-5. シェルソート
現在なお計算時間オーダーに関する未解決問題を孕んだミステリアスなソートです。挿入ソートを改良して、まず比較的離れた要素間で飛び飛びに大雑把に挿入ソートをしておいて、少しずつ比較する要素間の間隔を小さくしながらの挿入ソートを繰り返します。最後には通常の挿入ソートを行います。「挿入ソートはほとんど整列済みのデータには強い」という性質を活かしたソートだと言えます。ただし飛び飛びの要素を swap しているので安定ソートではなくなります。シェルソートの動きについては可視化動画「15 Sorting Algorithms in 6 Minutes」の 3:37 からあります。
離れた要素間で飛び飛びで挿入ソートするときのギャップの設定を gap sequence と呼び、シェルソートの性能を大きく左右する重要な選択となります。英語版 wikipedia に gap sequence の設定に関する改良史が詳細に記述されています。ここでは Marcin Ciura’s gap sequence (701, 301, 132, 57, 23, 10, 4, 1) を用いた実装を示します。
# include <iostream>
# include <vector>
using namespace std;
const int gaps[8] = {701, 301, 132, 57, 23, 10, 4, 1};
void ShellSort(vector<int> &a) {
for (int i = 0; i < 8; ++i) {
int g = gaps[i];
/* ギャップ g で挿入ソート */
for (int i = g; i < (int)a.size(); ++i) {
int v = a[i]; // 挿入したい値
int j = i; // 挿入する場所
for (; j >= g; j -= g) {
if (a[j - g] > v) {
a[j] = a[j - g];
}
else break;
}
a[j] = v;
}
}
}
int main() {
int n; // 要素数
cin >> n;
vector<int> a(n); // 整列したい配列ベクトル (サイズ を n に初期化)
for (int i = 0; i < n; ++i) {
cin >> a[i]; // 整列したい配列を取得
}
/* シェルソート */
ShellSort(a);
return 0;
}
10-6. コムソート
コムソートはマイナーではありますが、パズル愛好家などに人気のソートアルゴリズムでもあります。
バブルソートに少し毛を生やした程度の見た目で実装は非常にお手軽ながら、実験的には体感 $O(n\log{n})$ と言われるほど高速に動作するソートアルゴリズムです。クイックソートと同様、最悪ケースを引くと $O(n^2)$ とはっきり遅くなるようですが、最悪ケースを引くのは非常にレアであるという報告もあります。なお、コムソートも内部ソートではありますが安定ソートではないです。
挿入ソートをシェルソートへ改良するのと同様の改良を施します。ここでは gap を 1/1.3 倍ずつ縮めて行く実装をします。
# include <iostream>
# include <vector>
using namespace std;
void CombSort(vector<int> &a) {
int g = (int)a.size();
while (true) {
bool nonswaped = true; // swap されてないかどうか
g = max((g * 10) / 13, 1); // gap を縮める (1 以上にはする)
/* 間隔 g でバブルソートっぽく */
for (int i = 0; i + g < (int)a.size(); ++i) {
if (a[i] > a[i + g]) {
swap(a[i], a[i + g]);
nonswaped = false;
}
}
if (g == 1 && nonswaped) break; // g = 1 で swap なしなら break
}
}
int main() {
int n; // 要素数
cin >> n;
vector<int> a(n); // 整列したい配列ベクトル (サイズ を n に初期化)
for (int i = 0; i < n; ++i) {
cin >> a[i]; // 整列したい配列を取得
}
/* コムソート */
CombSort(a);
return 0;
}
10-7. ボゴソート
ネタです。配列のランダムシャッフルを繰り返して、それが整列済になっていたら止めるというものです。$n \le 10$ 程度までであればどうにか終了してくれますが、$n \ge 15$ となると宝くじで一等を当てる確率よりも低い確率が当たるまでシャッフルを繰り返さなければならず、非常に苦しいです。$n \ge 100$ となったら、宇宙が誕生してから今までの時間を 5000 兆回繰り返しても終了しないでしょう。
# include <iostream>
# include <vector>
# include <cstdlib>
using namespace std;
void Shuffle(vector<int> &a) {
int n = (int)a.size();
for (int i = n - 1; i > 0; --i) {
int k = rand() % (i + 1);
swap(a[i], a[k]);
}
}
void BogoSort(vector<int> &a) {
while (true) {
bool swapped = true;
for (int i = 0; i + 1 < (int)a.size(); ++i) {
if (a[i] > a[i + 1]) {
swapped = false;
}
}
if (swapped) break;
Shuffle(a);
}
}
int main() {
int n; // 要素数
cin >> n;
vector<int> a(n); // 整列したい配列ベクトル (サイズ を n に初期化)
for (int i = 0; i < n; ++i) {
cin >> a[i]; // 整列したい配列を取得
}
/* ボゴソート */
BogoSort(a);
return 0;
}
11. 参考書
ソートアルゴリズムを学ぶ上で参考になる書籍などを挙げていきます。
言わずと知れたアルゴリズムの世界的教科書です。前半の何章かはソートアルゴリズムの詳細な解析を行っています。
- プログラミングコンテスト攻略のためのアルゴリズムとデータ構造 (通称、螺旋本)
プログラミングコンテストを志す方向けの書籍ですが、様々なアルゴリズムやデータ構造を体系的に学べる書籍でもあります。オンラインジャッジを通して実際にソースコードを実装してジャッジすることにより、確かな理解度を獲得しながら学ぶことができます。ソートアルゴリズムにもかなりの紙面を割いて解説しています (個人的にはプログラミングコンテスト向けの書籍としてはソートに関する解説はもう少し省いてしまってもよかった気もしますが...)。
有名なソートからマニアックなソートまで、相当詳細に解説がなされています。英語版の方がより詳しく、内容の信憑性も高いです。
「8章 ソート」にて、各種ソートアルゴリズムの並行コンピューティング技法が詳細に議論されています。本記事はソートアルゴリズムを現代的な視点から捉え直したいという試みでしたが、その観点からは「ソートを並行処理する」というのは極めて重要な問題意識と言えるでしょう。クイックソートや基数ソートは、並行ソートとしても優れていることがわかります。
様々な言語でのソートライブラリの使い方を知るのに役立ちます。
12. なぜソートを学ぶのか
本記事のタイトルを回収します。現代のライブラリ充実環境において、ソートを学ぶ意味は
- ソートの使いどころを学ぶ
- ソートという題材を通して、様々なアルゴリズム技法を学ぶ
というところにあると思います。「どのソートが強いのか」という議論は、現代では
- 洗練されたソートアルゴリズムが実装されたライブラリが豊富にある
- ソートの内部性や安定性が本当に必要になる場面も少なくなった
といった理由により、重要性が薄れて来ている印象です。それよりも「ソートライブラリの使い方」や「ソートアルゴリズムの使いどころ」を学んで行く方が重要そうに思います。
一方ソートアルゴリズムは、計算オーダー改善、分割統治法、ヒープ、バケット、乱択アルゴリズムの思想といった様々なアルゴリズム技法を学べる格好の題材であることには変わりありません。本記事を通して「アルゴリズムとデータ構造」という分野の一端を感じ取っていただけたなら、とても嬉しく思います。