Ruby アルゴリズム 線形探索と二分探索

Rubyを通して線形探索と二分探索を学ぶ

##線形探索(リニアサーチ)
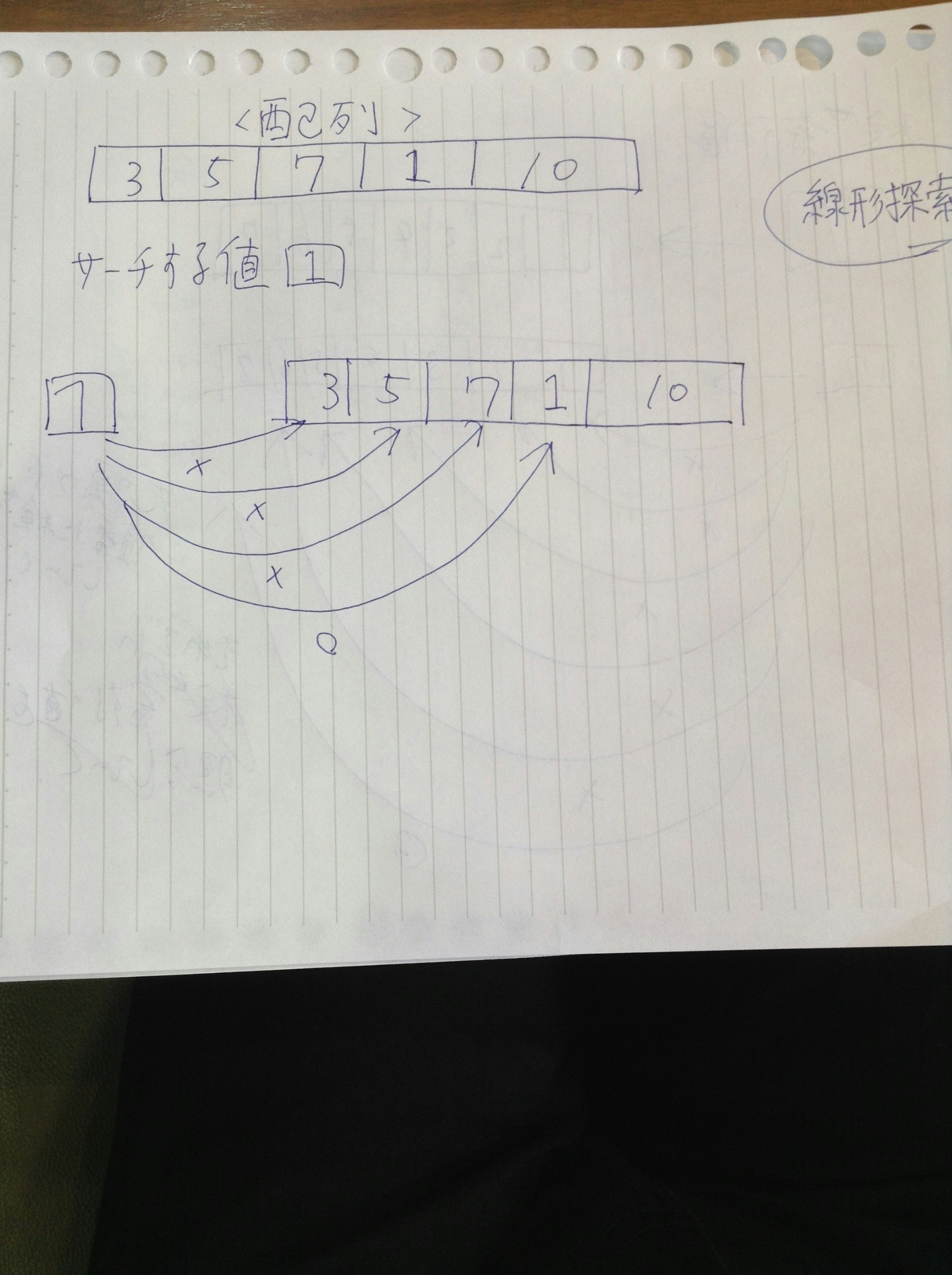
線形探索(リニアサーチ)とはリストの先頭から終端に向かって目的の要素を探し出すアルゴリズム。

とても単純で書きやすいアルゴリズムであるがリストのデータ量が多くなればなるほどに遅くなる。

def linear_search(arr_size, value)

  arr = (1..arr_size).to_a

  arr.each do |number|
    if number == value
      return "Found!"
    end
  end
end

下記イメージ図

##二分探索(バイナリサーチ)
二分探索(バイナリーサーチ)はソート済みの配列において、検索する間隔を半分に分割しながらデータを探し出すアルゴリズム
リニアサーチより高速であるがデータを必ずソートしなければならない

手順
１：配列を昇順もしくは降順にソートする。
２：配列の中央の要素を調べる
３：中央の要素が目的のデータより大きければ中央より後半の部分を調べる、また目的のデータより小さければ中央より前半の部分を調べる。
４：２に戻る

def binary_search(arr_size, value)
  arr = (1..arr_size).to_a

  left = 0
  right = arr.last
  mid = 0

  while left <= right do
    mid = (left + right) / 2
    if arr[mid] == value
      return "Found!"
    elsif arr[mid] < value
      left = mid + 1
    else
      right = mid - 1
    end
  end
end

下記イメージ図

##ベンチマークで検証

require 'benchmark'

#(以下省略)

puts Benchmark.measure { linear_search(1000, 100) }
puts Benchmark.measure { binary_search(1000, 100) }

=> 0.000000   0.000000   0.000000 (  0.000063)
=> 0.000000   0.000000   0.000000 (  0.000057)
 
puts Benchmark.measure { linear_search(100000, 10000) }
puts Benchmark.measure { binary_search(100000, 10000) }

=> 0.010000   0.000000   0.010000 (  0.004974)
=> 0.000000   0.000000   0.000000 (  0.004211)

puts Benchmark.measure { linear_search(100000, 99999) }
puts Benchmark.measure { binary_search(100000, 99999) }

=> 0.010000   0.000000   0.010000 (  0.011502)
=> 0.000000   0.000000   0.000000 (  0.004361)

検索範囲が大きくなればなるほど線形探索と二分探索の検索結果が大きくなっていく、また検索する対象が後尾になればなるほど二分探索の結果が早くなる。