こんにちは、大学 1 年生になったばかりの E869120 です。
私は競技プログラミング(競プロ)が趣味で、AtCoder や日本情報オリンピックなどに出場しています。ちなみに、2021 年 4 月 20 日現在、AtCoder では赤(レッドコーダー)です。
今回は、競技プログラミングにおける典型問題を毎朝投稿する「競プロ典型 90 問」という取り組みについて、そしてその活用方法について記します。
1. はじめに
皆さん、競技プログラミング(競プロ)をご存知でしょうか。
近年、競プロの存在感が急激に高まっており、最近では IT 業界・大学生・中高生の間でも広まっています。特に国内最大のコンテストサイトである AtCoder の知名度は相当高く、2017 年 9 月時点での参加登録者数は 3.7 万人であったのに対し、2020 年 6 月には 20 万人を突破し、現在もなお人気が伸び続けています。
しかし、競技プログラミングの実力を伸ばすのは決して簡単なことではありません。例えば AtCoder では、コンテストの成績に応じてレーティングが付けられるのですが、「9 割以上の企業においてアルゴリズム構築能力がカンストする」とされる黄色コーダーに到達するのは僅か 1.7%未満と極めて少なく、次表の通り **3 分の 2 以上が一番下の灰色コーダー**であるという事実があるのです。1
| 色 | 灰色 | 茶色 | 緑色 | 水色 | 青色 | 黄色 |
|---|---|---|---|---|---|---|
| レーティング | 1 以上 | 400 以上 | 800 以上 | 1200 以上 | 1600 以上 | 2000 以上 |
| 位置 | - | 上位 33% | 上位 19% | 上位 10% | 上位 5% | 上位 2% |
競プロにおける「上達の壁」
そこで私は、主に以下の 3 点が競技プログラミングにおける上達の壁になっているのではないかと考えています。
- 基礎的なコーディングの知識。for 文・条件分岐・配列などを使った基本的なプログラムが書けるかどうか。(レーティング 1~99 程度)
- 競プロで戦うために必要な、最低限のアルゴリズムや数学の知識。例えば二分探索・動的計画法・グラフ理論・逆元といったものが挙げられる。(レーティング 100~1199 程度)
- アルゴリズムや数学的知識 [2. で扱ったもの] をどうやって実際の問題に応用するか、考察面・実装面両方含めた典型テクニック。(レーティング 200~1999 程度)
今はどの壁が問題か?
現在、1. と 2. についてはかなり教材が整備されており、例えば 1. のプログラミングの基本を学ぶにあたっては、
- C++入門 AtCoder Programming Guide for beginners (APG4b)
- JOI 公式教材|Introduction to JOI
- Qiita|厳選!C++ アルゴリズム実装に使える 25 の STL 機能
などが参考になります。また、2. のアルゴリズム・数学の知識に関しては、次のような書籍や記事を読むことで身に付けることができます。
- 問題解決力を鍛える!アルゴリズムとデータ構造(通称:けんちょん本)
- プログラミングコンテスト攻略のためのアルゴリズムとデータ構造(通称:螺旋本)
- Qiita|アルゴリズム・AtCoder のための数学
一方、3. は他の 2 つと比べると教材が整っておらず、さらに近年も問題傾向が目まぐるしく変わっていることから、現在の出題傾向に沿った典型問題を解くのが一番の上達法だといわれています。
しかし、コンテストは週 1 回しか行われないため、コンテストだけでは練習量が少ないです。また、典型テクニックを集めた教材として「過去問精選 100 問」などもありますが、出題分野を知っている状態で過去問を解くのと、一から初見の問題を解くのでは、難易度やモチベーションの面で大きな差があり、人によっては合わないかもしれません。
「競プロ典型 90 問」のゴール
そこで、「競プロ典型 90 問」という新企画では、毎日新規問題を投稿することで、競プロ参加者のモチベーションを上げることに加え、多種多様な「典型アルゴリズムの活用方法」「典型考察テクニック」「実装テクニック」といったものを知ってもらい、最終的には
90 問全部を解いた後、競プロなどで要求される様々な問題解決のテクニックを網羅的に身に付けている状態になり、実力アップに繋げてもらうこと
を最大の目標にしています!!!
「競プロ典型 90 問」完成(2021/7/12 追記)
2021/7/11 に最後の問題が投稿され、90 問すべてが揃い、教材が完成しました。
今後は毎朝の投稿はありませんが、AtCoder 上で過去問として解くことができます。是非挑戦してみてください!!!
目次
| 章 | タイトル | 備考 |
|---|---|---|
| 1. | はじめに | |
| 2. | 競プロ典型 90 問とは? | この企画の説明をします |
| 3. | 初心者向け ~典型問題を解く前に~ | ここからサポートします |
| 4. | どのような問題が出題されるか? | 本記事のメインです |
| 5. | 典型 90 問を解くにあたって重要な 4 個のポイント | |
| 6. | おわりに |
2. 競プロ典型 90 問とは?
まず、「競プロ典型 90 問」とは、次のような企画です。
この企画の最大の特徴は問題が朝に投稿されることです。次のような理由があります。
- 1 日かけて問題の解法や実装方針を考えるには最適である
- 通勤・通学時間帯と重なるため、多くの参加者にとって、すき間時間を活用できる
- 大半のコンテストは夜遅い時間帯に開催されるため、コンテストにあまり参加できない、夜が苦手な人(主に中学生や高校生)への配慮ができる
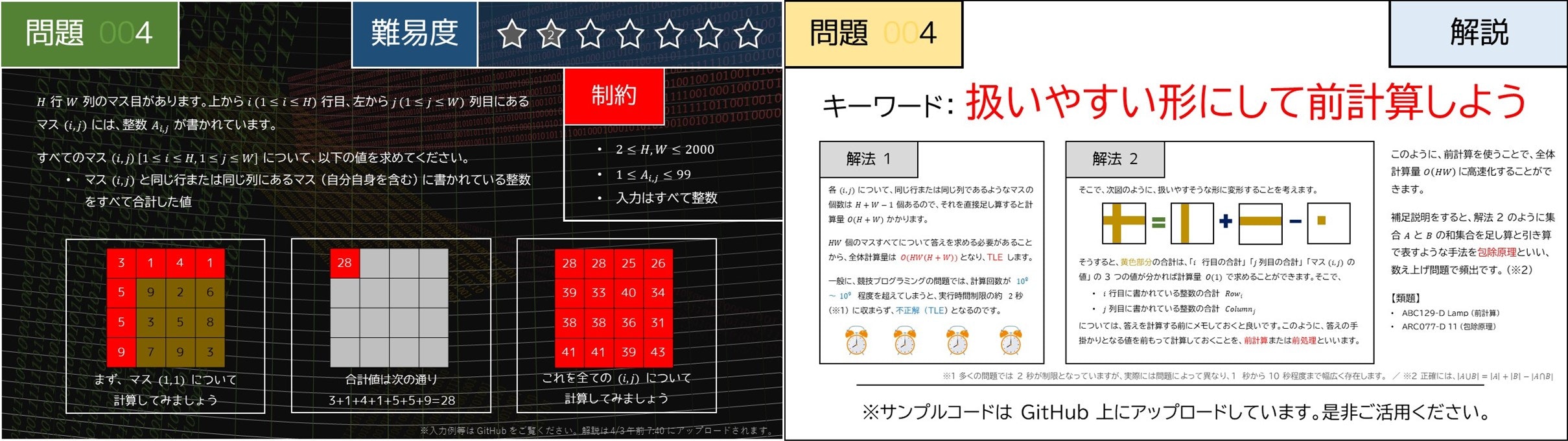
また、問題解説にも特徴があります。Twitter では新規問題や解説が下図のような感じで投稿されるのですが、解説では各問題のキーワードが載せられており、問題をふと振り返ったときに「どのような典型テクニックが問われるか」が一目でわかる作りになっています。
AtCoder での常設ジャッジ(2021/4/20 追記)
現在、この企画は概ね好評となっているため、AtCoder にてジャッジシステム(自分が書いたソースコードを提出し、正解を出すかどうか自動で判定を行ってくれるページ)が追加されました。リンクは次の通りです。
毎日 15 時頃に、その日の問題が AtCoder に追加され、提出ができるようになるシステムとなっています。4 月 20 日現在、19 個の問題が既に追加されています。また、各問題には難易度が付けられており、次表のようになっています。(Diff. は仮に AtCoder のコンテストに出題された場合、どのレーティング帯の半分の参加者が解きそうかを示しています)
| 星の数 | ★1 | ★2 | ★3 | ★4 | ★5 | ★6 | ★7 |
|---|---|---|---|---|---|---|---|
| 配点 | 1 点 | 2 点 | 3 点 | 4 点 | 5 点 | 6 点 | 7 点 |
| Diff. | ~149 | 150~399 | 400~799 | 800~1199 | 1200~1599 | 1600~1999 | 2000~ |
最後に、この企画はどんな層を対象としているのでしょうか。
対象とする実力層
「競プロ典型 90 問」は、基本的なプログラミングの知識が付いている、AtCoder レーティング 200(灰色上位)~ 1999(青色) 程度の層をメインターゲットにしています。
レーティング 199 以下の参加者は、
- 基本的なプログラミング言語の知識が身についていない
- AtCoder で出題される問題の形式に慣れていない
といったケースが多いので、もう少し簡単な問題を解くことを推奨しています。詳しくは 3 章をご覧ください。
ここまで、「競プロ典型 90 問」の概要について紹介しました。しかし、読者の中にはプログラミング始めたての人や、AtCoder に参加して間もない人もいると思うので、次章では典型 90 問に取り掛かる前にやるべきことについてまとめます。
3. 初心者向け ~典型問題を解く前に~
まず、競技プログラミングに参加したり、AtCoder の問題を解いたりするにあたって、以下の 2 つのことが前提条件として要求されます。
- あるプログラミング言語(C++ など)を用いて、プログラムを書けること
- AtCoder などのプログラミングコンテストで出題される問題のイメージをつかみ、問題形式に慣れること
では、どのようにすれば、このような能力が身につくのでしょうか。
3-1. プログラムを書けるようにする!
1 章でも紹介しましたが、現在 AtCoder では素晴らしい教材が整備されています。
この教材は、いわゆる "Hello World" と呼ばれる「出力するだけのプログラム」から、ループ・条件分岐・配列などの書き方、そして計算量やビット演算などアルゴリズムと直接関わる知識までカバーしています。ジャッジシステムが用意されているため、ソースコードを提出して正誤を確認することもできます。
3-2. AtCoder の出題形式に慣れる!
次に、競プロで出題される問題のイメージをつかむには、次の教材が最適です。
これは、@drken さんによって作成された「AtCoder の簡単な過去問を 10 問集めた教材」で、現在数万人が利用しています。AtCoder Beginner Contest (ABC) の A~C 問題レベルとなっており、プログラムの書き方を学んだ後に解く問題としては丁度良い難易度です。これもジャッジシステムが用意されています。
3-3. このレベル層にとって有効な記事
本章の最後に、AtCoder 始めたての人にとって良さそうな記事を紹介します。
です。この記事では AtCoder への登録方法から、過去問精選 10 問(AtCoder Beginners Selection)の解き方まで掲載されています。典型 90 問に取り掛かる前に、読んでおくと良いと思います。
この章では、「競プロ典型 90 問」を解くレベルに達する前に初心者がやるべきことについて紹介しました。次は 4 章、いよいよ本題です。この企画ではどのような問題が出題されるのか。皆さん、続きも是非お読みください。
4. どのような問題が出題されるか?
まず、競技プログラミングには様々な「典型」があります。詳しくは 4-3. 節で述べますが、頻出アルゴリズムとデータ構造だけでもこれだけあります2。(下に行けば行くほど難易度が上がります)
| 全探索 | 二分探索 | 深さ優先探索 | 幅優先探索 |
| 動的計画法(DP) | ダイクストラ法 | Warshall-Floyd 法 | クラスカル法 |
| 高速な素数判定法 | 冪乗を高速に計算する手法 | 逆元を計算する手法 | 累積和 |
| グラフ構造 | 木構造 | Union-Find | 座標圧縮 |
| 半分全列挙 | エラトステネスの篩 | ダブリング | Grundy 数 |
| Rolling Hash | 平方分割 | 最大流 | 最小カット |
| 最小費用流 | 二部グラフ判定 | 二部マッチング | FFT |
| 行列累乗 | Binary Indexed Tree | セグメント木 | 強連結成分分解 |
また、競プロで問われるのはアルゴリズムだけでなく、考察・実装の典型といったものもあります。AtCoder Beginner Contest (ABC) の D 問題までに出題されそうな範囲の中で、私が 2 分でパッと思いついたものだけでも、これだけあるのです。
- $N$ が小さい場合を考える(ARC117B など)
- 偶奇(パリティ)で場合分けして解く(ABC086C など)
- 全部調べ上げる変量を工夫して選んで全探索する(ABC085C など)
- $O(2^N)$ 系の全探索は 2 進数を用いた「bit 全探索」を使う(ABC197C など)
- 複雑な構造の全探索は再帰関数を使う(ABC196D など)
- 答えで二分探索して判定問題に落とす(ABC023D など)
- 誤差が気になるときは整数で処理する(ABC169C など)
- 3 つの要素 $i, j, k$ を扱うときは真ん中である 2 つ目を考える(ABC077C など)
- マンハッタン距離は 45 度回転すると整理しやすくなる(ABC178E など)
- 幾何問題は三角関数等を使って実装できることもある(ABC168C など)
- 余事象を考える(ABC193C など)
- $N \leq 16$ なら全探索など、制約から解法をエスパーする(ABC190C など)
- ある量でソートすると貪欲法が通用するようになる(ABC091C など)
- 辞書順最小問題は前から貪欲に決めていく(ABC076C など)
- マス目や座標を回転させることで実装量を減らす(JOI2020 二次予選 A など)
紙面の都合上これくらいにさせていただきますが、AtCoder Beginner Contest の E・F 問題に出題されるものを含めると、他にもたくさんあります。「競プロ典型 90 問」では、このような典型テクニックを網羅し、皆さんに様々なことを知ってもらうことを最大の目標にしています。しかし、文字数の都合上、本記事で全部説明することはできない上、あまりにも問題数が多いとネタバレになってしまうので、2 問に絞って紹介します。
4-1. 問題 010:Score Sum Queries(★2)
【問題概要】
大学には $N$ 人の一年生が在籍しており、クラスは $2$ つあります。学籍番号 $i$ 番の生徒は $C_i$ 組で、期末試験の点数は $P_i$ 点でした。
以下の形式の質問が $Q$ 個与えられるので、順に答えてください。
- 学籍番号 $L_i \sim R_i$ の $1$ 組生徒における、期末試験点数の合計
- 学籍番号 $L_i \sim R_i$ の $2$ 組生徒における、期末試験点数の合計
- これら $2$ つをそれぞれ求めよ。
【制約】
- $1 \leq N \leq 100000$
- $1 \leq Q \leq 100000$
- $0 \leq P_i \leq 100$
- $1 \leq C_i \leq 2$
- $1 \leq L_i \leq R_i \leq N$
- 入力はすべて整数
【数値例】
- $N = 7$
- $(C, P) = (1, 72), (2, 78), (2, 94), (1, 23), (2, 89), (1, 40), (1, 75)$
- $Q = 1$
- $(L, R) = (2, 6)$
- 答え:$(63, 261)$
【キーポイント】
- 累積和
【解法】
まず、以下のように for 文ループを用いたプログラムを書くと、全体計算量が $O(NQ)$ となります。競プロでは $10^8 \sim 10^9$ 回程度の計算回数しか許されないので、残念ながら**実行時間超過(TLE)**となってしまうのです。
// 入力部分は省略
for (int i = 1; i <= Q; i++) {
int Answer1 = 0, Answer2 = 0;
for (int x = L[i]; x <= R[i]; x++) {
if (C[x] == 1) Answer1 += P[x];
if (C[x] == 2) Answer2 += P[x];
}
cout << Answer1 << " " << Answer2 << endl;
}
そこで、累積和をメモする手法を考えてみましょう。具体的には、以下の値を持ちます。
- 学籍番号 $1 \sim i$ 番の $1$ 組生徒における、期末試験点数の合計 $S1_i$
- 学籍番号 $1 \sim i$ 番の $2$ 組生徒における、期末試験点数の合計 $S2_i$
例えば前述の数値例の場合、$S1, S2$ の値は次図の通りになります。$S1, S2$ のようなものを累積和といいます。
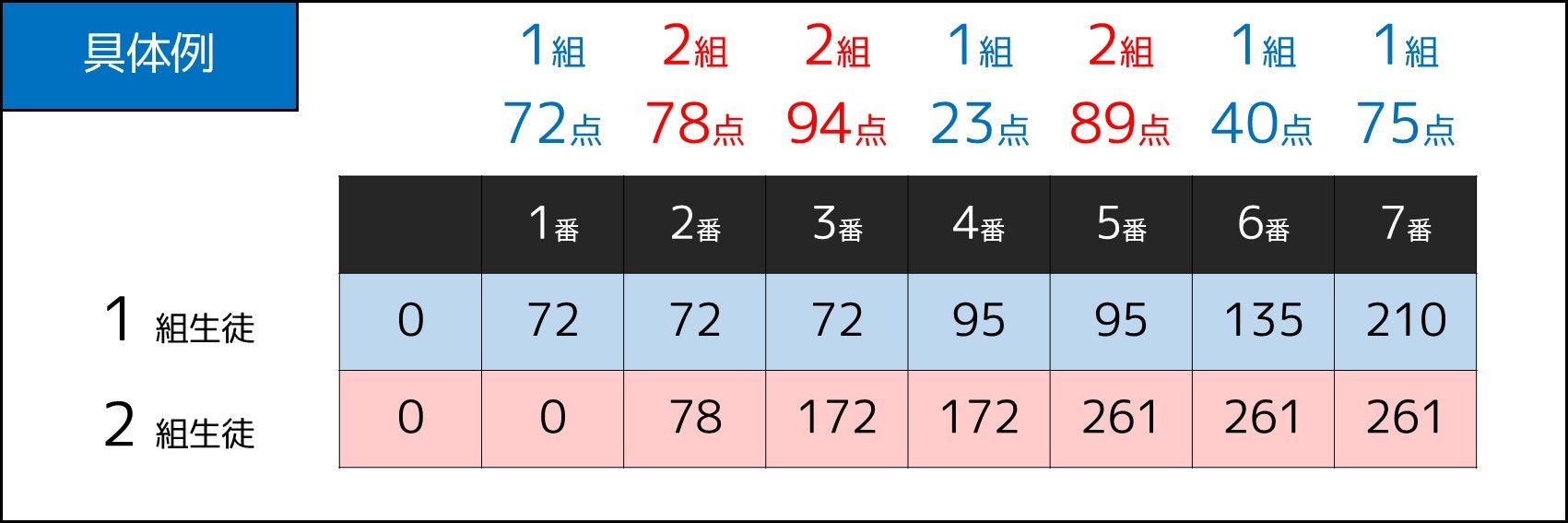
そこで、次のような性質が成り立つのです。
- 学籍番号 $L \sim R$ 番の $1$ 組生徒における、期末試験点数の合計は $S1_R - S1_{L-1}$
- 学籍番号 $L \sim R$ 番の $2$ 組生徒における、期末試験点数の合計は $S2_R - S2_{L-1}$
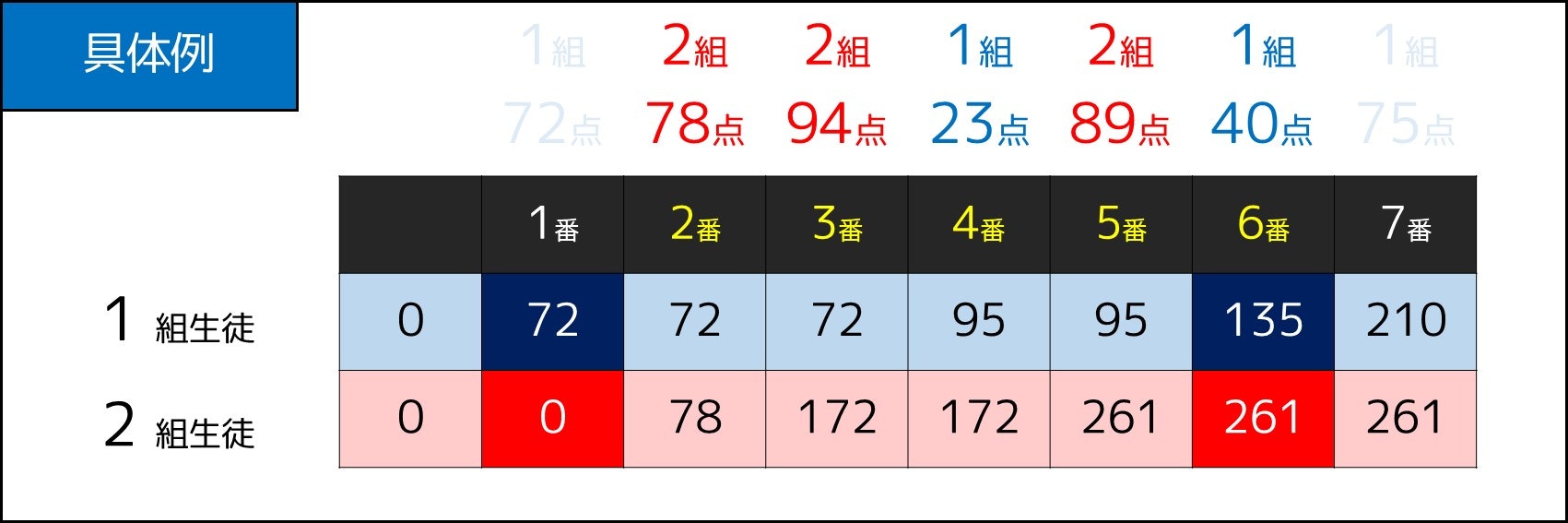
例えば下図の例で $(L, R) = (2, 6)$ の場合、
- $1$ 組生徒における期末試験点数の合計は $23 + 40 = 63$
- $2$ 組生徒における期末試験点数の合計は $78 + 94 + 89 = 261$
ですが、確かに $S1_6 - S1_1 = (135 - 72) = 63$、$S2_6 - S2_1 = (261 - 0) = 261$ となり、実に一致しているのです!!!
では何故そうなるのでしょうか。これは以下の性質が成り立つからです。
($L$ 番目から $R$ 番目の和)= ($1$ 番目から $R$ 番目の和)-($1$ 番目から $L-1$ 番目の和)
この手法を使うと、累積和 $S1, S2$ の計算に $O(N)$、質問に答えるのに $O(Q)$ かかるため、全体計算量は $O(N + Q)$ となります。プログラムは十分高速に動作し、正解(AC) を出すことができるのです。C++ での実装例は以下のようになります。
# include <iostream>
using namespace std;
// 入力
int N, Q;
int C[100009], P[100009], L[100009], R[100009];
// 累積和
int S1[100009], S2[100009];
int main() {
// Step #1. 入力
cin >> N; for (int i = 1; i <= N; i++) cin >> C[i] >> P[i];
cin >> Q; for (int i = 1; i <= Q; i++) cin >> L[i] >> R[i];
// Step #2. 1 組・2 組それぞれの累積和を取る
for (int i = 1; i <= N; i++) {
S1[i] = S1[i - 1];
S2[i] = S2[i - 1];
if (C[i] == 1) S1[i] += P[i];
if (C[i] == 2) S2[i] += P[i];
}
// Step #3. クエリに答える
for (int i = 1; i <= Q; i++) {
int Answer1 = S1[R[i]] - S1[L[i] - 1];
int Answer2 = S2[R[i]] - S2[L[i] - 1];
cout << Answer1 << " " << Answer2 << endl;
}
return 0;
}
【コメント】
最初の解法では $O(NQ)$ かかって実行時間超過すると書かれていますが、どうやって TLE するかどうかを見積もれば良いのでしょうか。実は目安があって、各計算量オーダーに対して $N$ が次表の値までであれば間に合うことが多いです。ただし、プログラムの性能の定数倍によって変動する場合があるので、注意してください。
| $O(\log N)$ | $O(N)$ | $O(N^2)$ | $O(N^3)$ | $O(2^N)$ |
|---|---|---|---|---|
| 何でもあり | 10^8 程度 | 10000 ~ 20000 程度 | 400 ~ 600 程度 | 20 ~ 25 程度 |
なお、場合によっては制約から想定解法の計算量オーダーを予測して、解法を絞り込むという考察テクニックが使える場合もあります。
【類題】
- JOI 2007 本選 1 - 最大の和
- JOI 2010 本選 1 - 旅人
- AtCoder Beginner Contest 177 C - Sum of product of pairs
- AtCoder Beginner Contest 182 D - Wandering
4-2. 問題 001:Yokan Party(★4)
【問題概要】
長さ $L$ [cm] のようかんに $N$ 個の切れ目があります。左から $i$ 個目の切れ目は、左から $A_i$ [cm] の位置にあります。
あなたは $N$ 個の切れ目のうち $K$ 個を選び、選んだ場所でようかんを $K+1$ 個のピースに分割したいです。そこで、以下の値をスコアとします。
- $K+1$ 個のピースのうち、最も短いものの長さ
スコアが最大となるように分割する場合に得られるスコアを求めてください。
【制約】
- $1 \leq K \leq N \leq 100000$
- $0 < A_1 < A_2 < \cdots < A_N < L \leq 10^9$
- 入力はすべて整数
【数値例】
- $N = 7$
- $L = 45$
- $K = 2$
- $A = (7, 11, 16, 20, 28, 34, 38)$
- 答え:$12$
例えば、左から 3 番目と 5 番目の切れ目を選んで分割すると、左のピースから順に 16 [cm]・12 [cm]・17 [cm] となり、スコアは 12 となります。
【キーポイント】
- 答えで二分探索
- 左から決めていく貪欲法
【解法】
まず、次のような問題が $O(N)$ で解けると仮定しましょう。
答えが $border$ 以上であるかどうか判定する問題。
詳しくは解法セクションの後半で述べる。
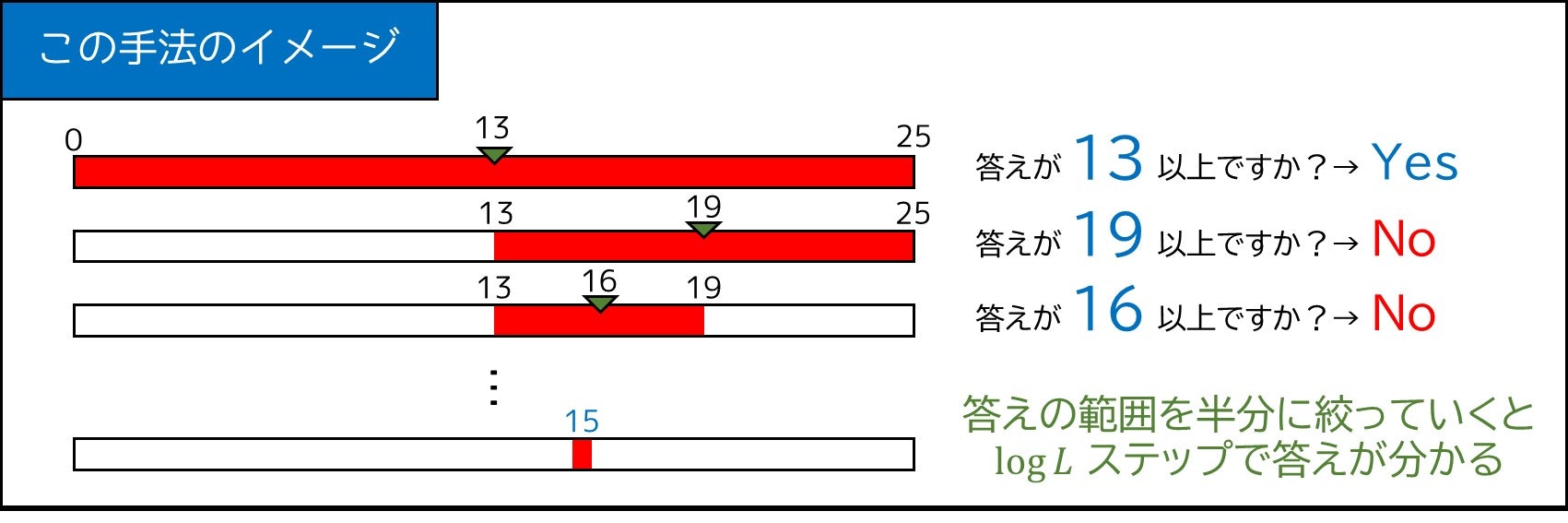
そこで、答えはどのようにして求められるのでしょうか。二分探索アルゴリズムを応用して、1 回の質問で探索範囲を半分に絞る、次のような手法が考えられます。(答えが $0$ 以上 $L\div(K+1)=15$ 以下であることが分かっているものとします)
| 質問 | 答え | 結論 |
|---|---|---|
| 答えは 8 以上か? | Yes | 答えの範囲は 8 ~ 15 に絞れる |
| 答えは 12 以上か? | Yes | 答えの範囲は 12 ~ 15 に絞れる |
| 答えは 14 以上か? | No | 答えの範囲は 12 ~ 13 に絞れる |
| 答えは 13 以上か? | No | 答えは 12 であることが分かる |
具体的に説明すると、アルゴリズムは次のようになります。
- 答えが $l$ 以上 $r$ 未満であることが分かっているものとする
- そこで、「答えは $(l+r) / 2$ 以上ですか?」という質問をする
- Yes の場合:この質問によって、答えの範囲が $(l+r) / 2$ 以上 $r$ 未満に絞れる
- No の場合:この質問によって、答えの範囲が $l$ 以上 $(l+r) / 2$ 未満に絞れる
このとき、答えとしてあり得る最大値を $L$ とするとき、答えを 1 通りに絞るまでに $O\lceil \log L \rceil$ 回の質問をする必要があります。
では次に後半パートを説明します。以下の問題はどうやって解けば良いのでしょうか。
答えが $border$ 以上であるか判定する問題
これは前半パートに比べれば簡単で、左の切れ目から順に考えて、一番ギリギリのところで貪欲に切っていけば良いです。例えば前述の数値例で $border = 12$ の場合、下図のようになります。
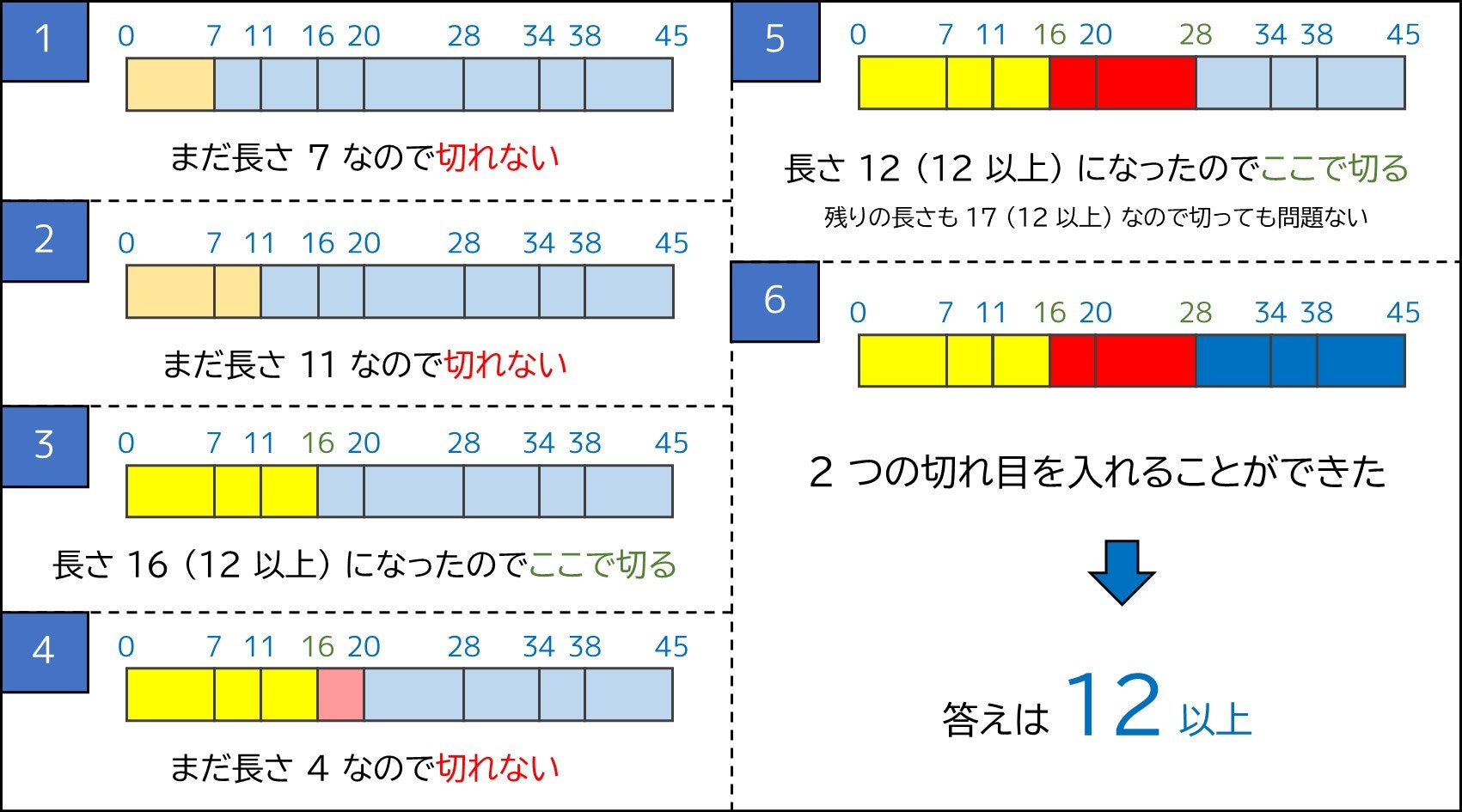
このように、答えで二分探索する典型テクニックと貪欲法を組み合わせることで、全体計算量 $O(N \log L)$ でこの問題を解くことができました。C++ での実装例は以下のようになります。
# include <iostream>
using namespace std;
long long N, K, L;
long long A[1 << 18];
bool solve(long long M) {
long long cnt = 0, pre = 0;
for (int i = 1; i <= N; i++) {
if (A[i] - pre >= M && L - A[i] >= M) {
cnt += 1;
pre = A[i];
}
}
if (cnt >= K) return true;
return false;
}
int main() {
// Step #1. 入力
cin >> N >> L;
cin >> K;
for (int i = 1; i <= N; i++) {
cin >> A[i];
}
// Step #2. 答えで二分探索
long long left = -1;
long long right = L + 1;
while (right - left > 1) {
long long mid = left + (right - left) / 2;
if (solve(mid) == false) right = mid;
else left = mid;
}
cout << left << endl;
return 0;
}
【コメント】
このように、「最大値を最小化してください」「最小値を最大化してください」といった系統の問題は、答えを二分探索することで高速に解けることが多いです。似たような系統の問題として、平均最大化というものもあり、これも一工夫すれば二分探索で解ける形になります。
【類題】
- AtCoder Beginner Contest 023 D - 射撃王
- Square869120Contest #5 B - Emblem
- AtCoder Regular Contest 101 D - Median of Medians
4-3. その他の問題たち
今回は紙面の都合上 2 問しか紹介できませんでしたが、他にも様々な問題が「競プロ典型 90 問」に収録されています。その中には、本記事で紹介しきれなかった典型も含めて、初級者向けの簡単な問題(★2程度)から上級者向けの難しい問題(★7)まで、様々なレベルのものが含まれています。
現在までに投稿されたすべての問題は
に掲載されていますので、皆さん是非解いてみてください。また、各問題で重要となるキーワードを含めた解説は、
に載っています。皆さん是非ご活用ください。
5. 典型 90 問を解くにあたって重要な 4 つのポイント
本記事の最後に、「競プロ典型 90 問」に出題される問題を解くにあたって重要なポイントを 4 つに分けて記します。
それぞれ、順番に説明していきたいと思います。
5-1. 解法が分かったら実装もしよう!
プログラミングコンテストでは、解法が分かっても正解(AC)を出すプログラムを提出しなければ得点できないため、例えば次のような参加者が多く表れます。
今日の ABC の D 問題、解法は分かったのに実装ができなかった。
このせいでレーティングが 20 落ちてしまった。
また、実装方針によっては実装量が膨大になる一方で、正しい実装方針を選ぶと楽に実装できるタイプの問題もあります。したがって、プログラムの実装に慣れるのは非常に重要です。
があるので、是非これを活用し、正解(AC)を出すところまでやりましょう。また、GitHub にサンプルコードが掲載されているので、これを見ても良いかもしれません。
5-2. 1 日考えて解けなかったら解説を見よう!
競技プログラミングでは、自分にとって難しい問題を長時間かけて考察することは非常に重要です。特に、非典型問題の正解が要求される橙色コーダー以上を目指すにあたっては必須の練習方法といえるでしょう。
しかし、この企画で投稿される問題は典型問題がほとんどで、アルゴリズムやテクニックを知っているかどうかがそのまま問われる場合もあります。したがって、その日に投稿された問題が翌朝になっても分からなかった場合、解説を見ることを推奨します。3
ただし、いくら典型とはいえ、考察を行う過程で学ぶことも非常に多いので、
30 秒考えても分からないので解説を見る
といった練習方法はおすすめしません。「1 日」が一つの目安ではないかと考えています。
5-3. 類題も解いてみよう!
解説を読むことで習得したアルゴリズムや典型テクニックも、1 つ問題を解くだけで、
- どのような問題に使えるかが分かるようになっている
- アルゴリズムの実装に慣れている
といった状態にできる人はほとんどいません。そこで、解説に載っている類題のうちいくつかを解いてみることをおすすめしています。
というサイトを使うことで AtCoder の過去問が全部見られるので、是非活用しましょう。なお、類題の中には本当に難しいものも含まれているので、全部解く必要はないと考えています。
5-4. コンテストに参加しよう!
最後に、最も重要なことを書きます。これはコンテストに出場することです。
いくら毎日問題が投稿されるとはいえ、同じアルゴリズム・典型テクニックが 90 問の中で 2 度出題されない場合も多く、一度習得したものを忘れる可能性もあります。したがって、コンテストで問題を解くことは、良い復習の機会になるのではないかと考えています。
また、コンテストで「競プロ典型 90 問」で出題された「典型」を使う問題が解けたとき、
あ、これ典型 90 問の「〇〇〇」で見たから解けた!!!!!
と嬉しい気持ちになると思います。このような面でも、モチベーションアップに繋がります。
6. おわりに
競技プログラミングでは、いわゆる「典型力」を付けることが大切です。つまり、様々な典型アルゴリズムや典型テクニックを知っておくこと、そしてどんな問題にこのような典型が使えるのかを理解しておくことが重要になってくるのです。
そこで、皆さんの「典型力」を高めることで全体の実力アップに少しでも貢献できればと思い、「競プロ典型 90 問」という企画を立案したので、一人でも多くの人が参加し有効活用していただけると、とても嬉しい気持ちです。
最後に、これは大学 1 年生が書いた記事なので、分かりにくい部分も多かったと思われますが、最後までお読みいただきありがとうございました。
謝辞
今回は、毎日 1 問アルゴリズムや競プロの典型問題を投稿する企画について書きました。これはおそらく、少なくとも私が調べた中では日本初の試みです。
そんな中、テストケース作成などに協力していただき、本企画の実現を可能なものにしてくださった Hec さん、ikd さん、kaage さん、Kazu1998k さん、kichi2004_ さん、m_99 さん、MMNMM さん、monkukui さん、Nachia さん、netyo715 さん、square1001 さん、tsutaj さん、yuto1115 さん、そして AtCoder の常設ジャッジを用意してくださった chokudai さん、そして競技プログラミングに関わるすべての方々に感謝申し上げます。本当にありがとうございました。