0. はじめに: クォータニオンについて思うこと
はじめまして!
NTTデータ数理システムで機械学習やアルゴリズムといった分野のリサーチャーをしている大槻 (通称、けんちょん) です。
本記事は、東京大学航空宇宙工学科/専攻 Advent Calendar 2018 の 3 日目の記事として書きました。僕は学部時代を工学部 航空宇宙工学科で過ごし、情報理工学系研究科 数理情報学専攻で修士取得後、現職に就いて数年になります。
航空宇宙時代は人工衛星の姿勢制御について関心を抱き、特に磁気センサや磁気トルカを用いた姿勢制御系について研究していました。数理工学へと分野を変えてからも、当時お世話になった先輩方と磁気トルカを用いた姿勢制御手法について共同研究して論文を書いたり、ディープラーニングなどを用いた画像認識技術を追求する過程ではリモートセンシングに関する話題ものぼったりなど、航空宇宙業界とは何かと強い繋がりを感じています。
本記事ではクォータニオンについて総整理します。クォータニオン (四元数) は、
などなど、幅広い分野で活用されているトピックです。航空宇宙業界と 3D ゲーム業界との両方で盛んに用いられているという点でとても興味深いです。特に最近では Unity の流行により、職業ゲームプログラマだけでなく、趣味で 3D ゲーム制作を楽しむ方にとっても、クォータニオンについて理解したいという方が増えているのを感じます。
本記事では、クォータニオンについて必要な事柄を総整理するとともに、クォータニオンをワカッタ感覚で納得することを目標にします。
1. クォータニオンを用いてやりたいこと
そもそもクォータニオンを使って何がやりたいのでしょうか?大きく分けて以下の 2 つがあるように思います。
- 3D 空間における「回転」を表す
- 3D 物体の「姿勢」を表す
2 つと言ったのですが、メインは「回転」の方でしょう。「姿勢」は単純に「どういう回転でその向きになったか」として捉えることができます。
注意点として、「姿勢」は「方向」よりも多くの情報を含んでいます。クォータニオンを用いた回転を扱うときに、回転させたい対象が「姿勢」なのか「方向」なのかを混乱しないようにすることが肝要です。方向は「進行方向」や「視線」といったものを表していますが、姿勢はそれに加えて、その方向周りの角度の情報も含みます。航空機でいえば、機首の向いている方向だけでなく、機首に対して機体がどれだけ傾いているのかも指定してはじめて機体の姿勢が完全に決まります。数理的には以下のようになっています。
| 自由度 | 備考 | |
|---|---|---|
| 方向 | 2 | 進行方向は三次元ベクトル (3 個のパラメータ) で表せますが、そのベクトルの大きさは意味を持たないので 1 減らして 2 です |
| 姿勢 | 3 | 方向 + 1 です |
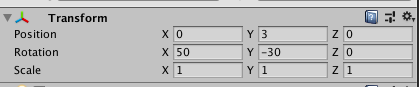
つまり、姿勢は最小 3 個のパラメータで表せるということです。回転も姿勢と本質的に同じものなので、同様に 3 個のパラメータで表せます。実際にオイラー角は 3 個のパラメータで姿勢や回転を表します (回転を表す方法はクォータニオンだけではなく、オイラー角による方法もメジャーな方法の 1 つです)。オイラー角は Unity ではインスペクターの Rotation 項目で表示されているやつです (しかし transform.rotation は Quaternion 型なので少し紛らわしいですね...この記事でも注意喚起がなされています)。
そして後述するようにクォータニオンは 4 個のパラメータで姿勢を表すので、それらに何の制約もないと冗長になります (姿勢を表す方法が一意に定まらず、1 自由度残ってしまう)。ですのでその 4 個のパラメータを縛る制約が 1 つあります。具体的には「ノルムが 1」という制約です。
さらに姿勢や回転を表す表現方法にはもう 1 つ回転行列 (または基底変換行列という DCM とも呼ばれるもの) があり、9 個のパラメータ (3 × 3 行列) で表します。それらを縛る制約は「正規直交行列である」です。
1-1. クォータニオンとは
クォータニオンは任意軸回転がキーワードとして言及される場面も多いです。いかなる回転 (三次元空間内) も表現できることが強みです。具体的には以下のように定義します。
三次元空間において
- 方向ベクトル $(\lambda_x, \lambda_y, \lambda_z)$ を回転軸として
- 角度 $\theta$ だけ回転する
という「回転」を表すクォータニオンは、四次元ベクトル $(\lambda_x \sin{\frac{\theta}{2}}, \lambda_y \sin{\frac{\theta}{2}}, \lambda_z \sin{\frac{\theta}{2}}, \cos{\frac{\theta}{2}})$ で表します。
これらは Unity では、Quaternion 型変数を qua として、
- qua.x = $\lambda_x \sin{\frac{\theta}{2}}$
- qua.y = $\lambda_y \sin{\frac{\theta}{2}}$
- qua.z = $\lambda_z \sin{\frac{\theta}{2}}$
- qua.w = $\cos{\frac{\theta}{2}}$
という風に対応しています (が、Unity の Quaternion を扱うときにこれらの成分を直接触ることはあまりないかもです...スクリプトリファレンスにもクォータニオンに熟知していない限りは x, y, z, w の値を直接変更しないでくださいと書いてあります)。また Unity で上記の定義に則ってクォータニオンを生成するときは Quaternion.AngleAxis を用います (オイラー角など他の方法でクォータニオンを生成する方法は後述します)。
// Y 軸 (上方向) まわりに 30 度回転するのを表すクォータニオン
Quaternion.AngleAxis(30, Vector3.up)
ところで上の定義を見ると
- なんでいきなり三角関数が...
- $\frac{\theta}{2}$ ってなんだよ... $\theta$ でいじゃん...
と思ってしまいそうです。その答えは「こう定義すれば具体的な回転計算が超楽だから」なのですが、本記事を読み進めて行くことで少しずつ実感していただけたらと思います。
1-2. クォータニオンによる回転操作
クォータニオンによる「回転」を定義したからには、実際に「三次元ベクトル」や「姿勢」を回転させる計算方法を導出してあげる必要があります。三次元ベクトル $\vec{v}$ の回転計算は
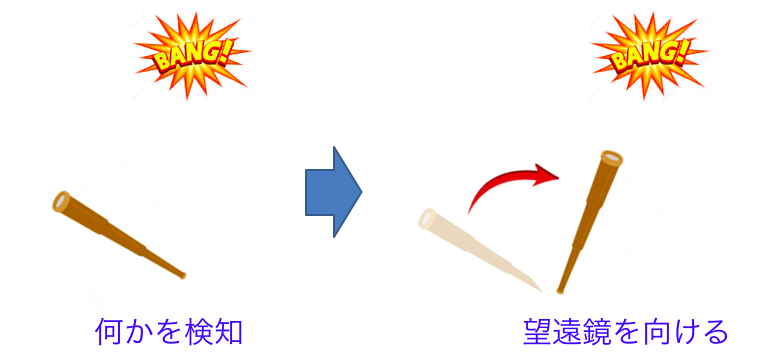
- キャラクターの視線をある方向へと徐々に向けて行く (3D ゲーム)
- 宇宙機に搭載した望遠鏡を所望の方向へ向ける (航空宇宙)
といった場面で必要になります。
また、姿勢 $p$ の回転計算は、
- クォータニオンとクォータニオンの補間 (3D ゲーム)
- 航空機や宇宙機の三軸姿勢制御 (航空宇宙)
といった場面で必要になります。
結論としては、三次元ベクトル $\vec{v}$ や姿勢クォータニオン $p$ に対し、回転 $q$ を実施した結果は以下のように大変シンプルなものになります!!!!!!!
| 回転させるもの | 回転結果 | 備考 |
|---|---|---|
| ベクトル $\vec{v}$ | $q \otimes \vec{v} \otimes \bar{q}$ | $\bar{q}$ は $q$ の逆回転 |
| 姿勢クォータニオン $p$ | $q \otimes p$ |
逆に
回転操作をシンプルな計算で実現できるように、クォータニオンをあのように定義した
とも言えます。なお、クォータニオン同士のかけ算 $q \otimes p$ や、クォータニオンとベクトルとのかけ算 $q \otimes \vec{v}$ はまだ定義していないですが、1-4 で導入します。また、こうした事柄はクォータニオンを自分で実装する場合には必要な知見なのですが、Unity ではいずれも単に
v2 = q * v // 三次元ベクトル v の回転
p2 = q * p // 姿勢 p の回転
と「*」演算子で実現することができます。$q \otimes \vec{v} \otimes \bar{q}$ な量を q * v と記述するのは少し紛らわしさがありますが、実用上とても簡便です。演算子の順番は重要で、左右を入れ替えてはダメです。
1-3. なぜクォータニオンなのか
三次元空間上での回転や姿勢を表現する方法には代表的なものが 3 つあります。
| パラメータ数 | メモリ消費 | 計算上の扱いやすさ | 備考 | |
|---|---|---|---|---|
| クォータニオン | $4$ | ⚪︎ | ◎ | バランス型で、その他様々なメリットがあります |
| オイラー角 | $3$ | ◎ | × | 具体的な姿勢をイメージしやすく、メモリ的にも優しいですが、計算上の難点を抱えています |
| 回転行列 or DCM | $9$ | × | ⚪︎ |
どの方法にもメリット・デメリットがあるので、状況に応じて使いこなせばいいのですが、総じてクォータニオンはバランスがとれた優秀な方法であることがわかります。
オイラー角はたった 3 個のパラメータで回転や姿勢を表現できるので、メモリ消費は少なくて済むのですが、三角関数を多用することもあって計算時間的には大きくなってしまいます。それどころかもっと悪いことに、オイラー角の二番目の角度が $±90$ 度になる場合が特異点となって計算上の大きな問題を引き起こすことが知られています (詳しくはジンバルロックを参照)。端的に言えば、ヨーとロールの区別ができなくなってしまう状態です。しかしながら特に航空機の世界では
- そもそもジンバルロックが起こるような状態にならない (ピッチが $±90$ 度になる状態...下図のような墜落時などに発生しそうな相当ヤバイ状態です...戦闘機などでは考慮が必要です)
- ヨー、ピッチ、ロールという概念がとてもなじみ深い
といった理由によって盛んに用いられています。また、3D ゲームの世界などにおいても、オイラー角の直感的なイメージしやすさから、UI や API 部分では用いられるケースも多いです。
次に回転行列についてですが、実は回転行列とクォータニオンは本質的には同じものです (数学的には準同型性によって繋がっています)。回転行列は 9 個のパラメータで表すのに対し、
回転行列のもつ性質を失わずに、4 個のパラメータに圧縮したものがクォータニオンである
と言えるでしょう。それだけでなく数値的にも数値誤差を生じにくくなることが知られています。まとめるとクォータニオンは
- メモリ的にもそこそこ優しく
- 計算時間的にもとても速く
- 回転行列の性質を引き継いでいるので回転の結合計算も容易にできて
- ジンバルロックなどの計算上の問題を引き起こすこともなく
- 計算時に数値誤差を生じにくく (この記事を参照)
- 回転の連続的変化や補間計算もしやすい (この記事を参照)
ということで、非常にバランスのとれた優秀なステータスをしていることがわかります。唯一のデメリットは
クォータニオンが与えられたときに、具体的な回転や姿勢をイメージしにくい
くらいでしょうか...この対策としては
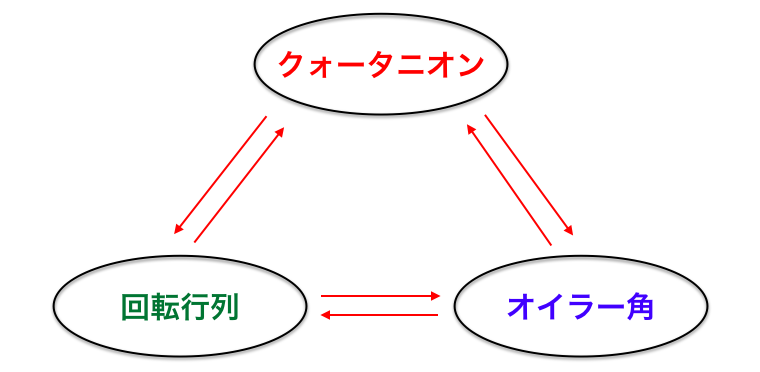
- クォータニオンからオイラー角への変換 (とその逆)
- クォータニオンから回転行列 (DCM) への変換 (とその逆)
を押さえることが挙げられます。なお、「クォータニオン」「オイラー角」「回転行列 (DCM)」はすべて簡単な計算で相互変換が可能です。ここではクォータニオンから回転行列への変換を下に挙げます。
\begin{pmatrix}
q_x^2-q_y^2-q_z^2+q_w^2 & 2(q_xq_y-q_zq_w) & 2(q_xq_z+q_yq_w) \\
2(q_xq_y+q_zq_w) & -q_x^2+q_y^2-q_z^2+q_w^2 & 2(q_yq_z-q_xq_w) \\
2(q_xq_z-q_yq_w) & 2(q_yq_z+q_xq_w) & -q_x^2-q_y^2+q_z^2+q_w^2
\end{pmatrix}
その他についてはこの資料などが詳しいです。
1-4. クォータニオンのかけ算
クォータニオンの演算について中身を特に知る必要がない場合には「2. クォータニオンの使い方」まで飛ばしていただけたらと思います。
さて、「1-2. クォータニオンによる回転操作」では、クォータニオンのかけ算を定義することなく持ち出してしまいました。クォータニオンのかけ算は以下のように定義します。
クォータニオン $p = (p_x, p_y, p_z, p_w)$ に対して、回転クォータニオン $q = (q_x, q_y, q_z, q_w)$ を施して得られるクォータニオンは
\begin{align}
q \otimes p = (
&q_w p_x - q_z p_y + q_y p_z + q_x p_w, \\
&q_z p_x + q_w p_y - q_x p_z + q_y p_w, \\
&-q_y p_x + q_x p_y + q_w p_z + q_z p_w, \\
&-q_x p_x - q_y p_y - q_z p_z + q_w p_w)
\end{align}
で与えられる。
ここで、$q \otimes p$ などは $qp$ と略記することが多いです。また上記の式は行列を用いるとスッキリと見通しよく書くこともできます。
qp =
\begin{pmatrix}
q_w & -q_z & q_y & q_x \\
q_z & q_w & -q_x & q_y \\
-q_y & q_x & q_w & q_z \\
-q_x & -q_y & -q_z & q_w
\end{pmatrix}
\begin{pmatrix}
p_x \\
p_y \\
p_z \\
p_w
\end{pmatrix}
大変シンプルな計算で回転計算ができることがわかります。「どこからこんな式が出て来るんだ...」という感じではありますが、3-2 で見るようにクォータニオンが複素数を自然に拡張したものであることを思い出すと、上記の式も自然に導くことができます。
また、クォータニオンと三次元ベクトルとをかけ算するときは、三次元ベクトル $\vec{v} = (v_x, v_y, v_z)$ をクォータニオン $(v_x, v_y, v_z, 0)$ と同一視してかけ算します。したがって、クォータニオンと三次元ベクトルとの積はクォータニオンになります。注意点として、三次元ベクトル $\vec{v}$ をクォータニオン $q$ によって回転して得られる三次元ベクトルは $q\vec{v}\bar{q}$ であると紹介したのですが、一見これはクォータニオンに見えます。しかし実際に計算すると必ず w 成分が $0$ になって $(r_x, r_y, r_z, 0)$ の形になるので、$q\vec{v}\bar{q}$ を再び三次元ベクトルに戻すことができます。
最後にクォータニオンのかけ算の式を見ていると、ベクトルの外積が思い浮かびます。実際密接な関係があり、
クォータニオンの w 成分を $0$ にしてかけ算計算したものは、ベクトルの外積に対応している (計算結果の w 成分を無視します)
ことがわかります。このことを逆に利用するとクォータニオンのかけ算を、ベクトルの外積を用いて表すことができて、具体的にはクォータニオン $q = (q_x, q_y, q_z, q_w)$ を $q = (\vec{q_v}, q_w)$ と表すことにすると、
\begin{align}
qp
&= (\vec{q_v}, q_w) \otimes (\vec{p_v}, p_w) \\
&= ((\vec{q_v} \times \vec{p_v} + p_w\vec{q_v} + q_w\vec{p_v}), (q_w p_w - \vec{q_v} \cdot \vec{p_v}))
\end{align}
と計算できます。
1-5. クォータニオンの定義についての注意点
注意点 1: 回転方向 (右手系と左手系)
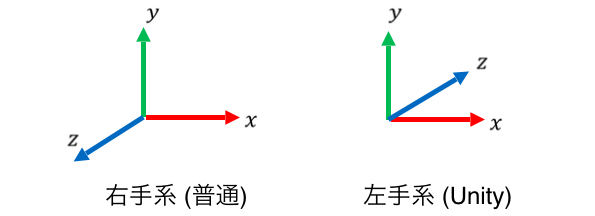
航空宇宙業界やその他多くの業界でクォータニオンを扱う場合はほぼすべて右手系の座標系を用いる一方で、Unity では
- x 軸方向: 右
- y 軸方向: 上
- z 軸方向: 前
という風に左手系が採用されているというややこしい事情があります。なお下図は右手系の一例を示していますが、具体的な座標系の取り方はフレームワークによって様々なものがあるようです (この記事を参照)。
この違いによるクォータニオンへの影響としては、
- 右手系では回転方向は反時計回りを正の向きとして測る
- 左手系では回転方向は時計回りを正の向きとして測る
と考え直す必要があります。しかし実際上は難しく考えずに「Unity では角度を時計回りで考える」とだけ認識していれば問題ないことが多いです。こういった事情に関する話は、詳しくはこの記事を参考にしていただけたらと思います。
注意点 2: 回転クォータニオンのノルムは 1
上の自由度に関する議論と関連するのですが、クォータニオンの定義において回転軸 $(\lambda_x, \lambda_y, \lambda_z)$ は、通常ノルムは $1$ に統一して考えます。つまり $\lambda_x^2 + \lambda_y^2 + \lambda_z^2 = 1$ とします。回転軸は「方向」だけが重要で大きさには意味がないので、ノルムを $1$ に統一するのは自然です。
そしてこのとき、クォータニオンのノルムも必ず $1$ になります:
\begin{align}
\lambda_x^2 \sin^2{\frac{\theta}{2}}
+ \lambda_y^2 \sin^2{\frac{\theta}{2}}
+ \lambda_z^2 \sin^2{\frac{\theta}{2}}
+ \cos^2{\frac{\theta}{2}}
&= (\lambda_x^2 + \lambda_y^2 + \lambda_z^2)\sin^2{\frac{\theta}{2}}
+ \cos^2{\frac{\theta}{2}} \\
&= \sin^2{\frac{\theta}{2}} + \cos^2{\frac{\theta}{2}} \\
&= 1
\end{align}
また反対に、ノルムが $1$ の四次元ベクトルは、必ず何らかの回転を表すクォータニオンになっていることもわかります。なお Unity の Quaternion.AngleAxis を用いるときに指定する回転軸はノルムが $1$ でなくても内部で $1$ になるように正規化してくれるようです。
注意点 3: もう 1 つのクォータニオン
実は、同一の回転を表すクォータニオンは一意ではなく、クォータニオン $q = (q_x, q_y, q_z, q_w)$ に対して全要素の符号を反転したクォータニオン $−q=(−q_x, −q_y, −q_z, −q_w)$ もまったく同一の回転を表すクォータニオンになります。つまり、回転軸も回転方向も逆方向にした回転は、元の回転と同じ回転になっています。
似て非なるものとして、共役クォーニタオン $\bar{q} = (−q_x, −q_y, −q_z, q_w)$ は「逆回転」を表しています。Unity では Quaternion.Inverse に対応しています。
2. クォータニオンの使い方
いよいよクォータニオンの実際の使い方について見て行きます。
まずは 1 番目のクォータニオンの生成方法がすべての基本になります。具体的に実現したい回転運動があっても、それをクォータニオンで表す術を知らなければ何もできなくなってしまいます。
そして 2 番目は主に Unity での応用を意識しており、3 番目以降は主に航空宇宙での応用を意識しています。Unity では三次元物体の回転や姿勢状態はプログラマがすべて把握して天下りに指定することが多いので、クォータニオンを連続的に変化させていく方法が重要になります。一方航空宇宙では航空機・宇宙機の姿勢状態は現実世界の物理法則に則っているので、姿勢状態をシミュレーションしたり、推定・制御したりする手法が重要になります。
2-1. クォータニオンの生成
クォータニオンを使う立場にとって真っ先に重要なことは、具体的に実現したい回転をクォータニオンとして表す方法を習得することでしょう。以下の 3 つが代表的だと思います。3 番目に挙げた Unity 関数 Transform.LookAt はクォータニオンを返すものではないですが、物体を回転させる操作を行います。いずれも頻繁に用いられるものですが、特に 3 番目の LookAt は使い勝手がよくて便利です。
| 指定するもの | Unity 関数 | 備考 | |
|---|---|---|---|
| 1 | 回転軸と回転角度 | Quaternion.AngleAxis | クォータニオン本来の定義 |
| 2 | オイラー角 | Quaternion.Euler | 角度を 3 つ指定します |
| 3 | 向けたい方向 | Transform.LookAt | 今の向いてる方向 (デフォルトで上方向) と、向けたい方向を指定します |
関数の使い方の補足
1 番目と 2 番目について、基本的には
- 回転させたいもの (姿勢 Quaternion や、方向ベクトル Vector3) がある
- 実現したい回転を表すクォータニオンを作る
- 「*」演算子を適用して回転させる (1-2 を参照)
という使い方になりますが、回転させたいものが特に Transform 型そのものの場合は、Transform.Rotate を直接適用してしまうのが早いと思います。そのあたりのことはこの記事に詳しく書かれています。
- ある回転軸まわりの、ある角度の回転
- オイラー角を指定しての回転
の両方に対応している便利関数です。
Transform.LookAt について
とにかく難しいことを考えずに「指定した方向を向かせたい」ときに使えるとても便利な関数です。カメラを特定のものを注視させる処理を簡単に実現できます。こちらも
にとても詳しく載っています。
オイラー角について
オイラー角の定義には様々な流儀があるのですが、例えば Unity では
- Z 軸まわりに $\psi$ だけ回転
- 新たな X 軸まわりに $\theta$ だけ回転 (1 の回転後の X 軸まわり)
- 新たな Y 軸まわりに $\phi$ だけ回転 (2 の回転後の Y 軸まわり)
という回転を $(\psi, \theta, \phi)$ と表し、オイラー角と呼びます。ここでは「Z 軸 -> X 軸 -> Y 軸」の順で書いたのですが、この順番には様々な異なる流儀があり、状況に応じて使い分けることになります。
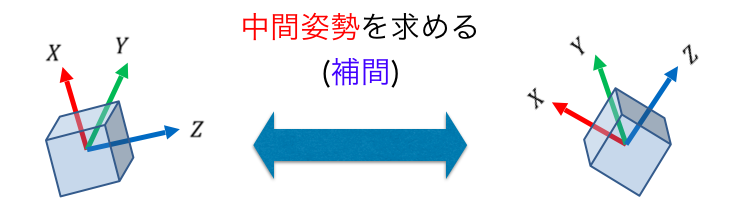
2-2. クォータニオンの連続的回転・補間
これはいわゆる Unity でおなじみの球面回転補間 Quaternion.Slerp ですね。回転状態 $q_1$ と回転状態 $q_2$ の中間の状態をいとも簡単に求めることができます。
Quaternion.Slerp の使い方自体はとても簡単で、例えば
float t = Time.time;
Quaternion from_qua = Quaternion.Euler(0f, 0f, 0f);
Quaternion to_qua = Quaternion.Euler(0f, 0f, 90f);
this.transform.rotation = Quaternion.Slerp(from_qua, to_qua, t);
という感じに使えます。Quaternion.Slerp の第三引数 $t$ は $[0, 1]$ の範囲で指定します。$t = 0$ なら from_qua に一致し、$t = 1$ なら to_qua に一致します。上のコードは 1 秒で 90 度回転する処理になっています。
なお、クォータニオンの大円補間に関しては幾何学的に大変美しく明快な構造があります。この記事にとても詳しく書かれているので、是非読んでみるととても面白いです。
2-3. クォータニオンのシミュレーション
航空宇宙では航空機や宇宙機は物理法則に則った回転運動をします。そのため姿勢制御のためにはシミュレーション技術が欠かせません。
- 予め様々な環境での挙動をシミュレートする
だけでなく運用時に
- 角速度を積分した情報も組み合わせて、高精度な姿勢推定を行う (カルマンフィルタなど)
ためにも、姿勢に関する微分方程式が必要になります。大きく分けて 2 つの微分方程式があります。
- 純粋に「角度を微分したら角速度」を記述したもの (キネマティクス)
- いわゆる「剛体の回転運動方程式」を記述したもの (ダイナミクス)
クォータニオンを用いるとそれぞれ簡単に表すことができて、キネマティクスを表す微分方程式は角速度を $(\omega_x, \omega_y, \omega_z)$ として
\dot{q} =
\frac{1}{2}
\begin{pmatrix}
0 & \omega_z & -\omega_y & \omega_x \\
-\omega_z & 0 & \omega_x & \omega_y \\
\omega_y & -\omega_x & 0 & \omega_z \\
-\omega_x & -\omega_y & -\omega_z & 0
\end{pmatrix}
\begin{pmatrix}
q_x \\
q_y \\
q_z \\
q_w
\end{pmatrix}
となります。これはクォータニオンとベクトルとのかけ算の表記を用いると
$$\dot{q} = \frac{1}{2}q\omega$$
と簡単に書くことができます。数値シミュレーションを行ったり、拡張カルマンフィルタを構築したりする場合には、これを差分方程式の形にします。次にダイナミクスは航空機や宇宙機の慣性テンソルを $I$、はたらくトルクを $T$ として、
\frac{d^B}{dt}(I\omega) = T -\omega \times I\omega
が成立します。ここで $\frac{d^B}{dt}$ は機体座標系において成分ごとに微分することを意味しています。特に機体座標系を慣性主軸にとると (慣性テンソルが対角成分以外が $0$ となるようにとると)、以下のように展開できます。
I_x \dot{w_x} = T_x + (I_y - I_z) \omega_y \omega_z \\
I_y \dot{w_y} = T_y + (I_z - I_x) \omega_z \omega_x \\
I_z \dot{w_z} = T_z + (I_x - I_y) \omega_x \omega_y
2-4. クォータニオンを用いた姿勢推定・制御
姿勢制御を行う前にまずは自身の姿勢状態を推定するタスクが非常に大切です。研究開発の場面では姿勢推定をひたすら頑張ることが多く、むしろ凝った制御を行わない限りは、姿勢推定ができれば姿勢制御系は機械的に PID フィードバック制御系を組むなどして導出できることが多いです。
姿勢推定する方法は大きく分けて 2 つの方向性があります。それぞれにメリット・デメリットがあります。
- スターセンサなどを用いて、座標変換などを利用して直接姿勢を求める
- ジャイロセンサなどを用いて角速度を測定し、それを数値積分する
1 の方法は高精度に姿勢を推定できる場合が多いです。また、データを積分することによる数値誤差の蓄積の影響もなく、姿勢が大きく変化しているような状況にも対応できます。しかしながら欠点としては、姿勢を観測する周期が長く (数 Hz くらいの感じ)、超高精度な姿勢制御を行う場合にはとても間に合わなくなることが挙げられます。他に機体座標系の構造のミスアライメントの影響を直接受けることもデメリットとして挙げられます。
2 の方法はそれ単体では成立しないでしょう。角速度を積分していくうちに数値誤差が蓄積して行きますし、ジャイロセンサ自体のもつバイアス誤差も蓄積して行きます。しかしながら、ジャイロセンサは計測に関わる応答動作が迅速であり、非常に短い観測周期を達成することができます (数百 Hz くらいの感じ)。なお、この方法を用いるときは前節で紹介したキネマティクス微分方程式を用います。
これらの方法のよいところどりを目指した方法として、拡張カルマンフィルタを用いた方法が、現在航空宇宙における姿勢推定系のデファクトスタンダードになっています。基本的にはジャイロセンサの計測した角速度を数値積分しつつ、時々得られるスターセンサからの計測値を用いて「尤もらしい値を推定する」という手法です。ジャイロセンサのもつバイアスも一緒にまとめて推定してしまうというカッコイイ方法です。
ここでは 1 の方法の指針を簡単に紹介します。まず、回転行列について考察します。回転行列は DCM (基底変換行列、方向余弦行列) であるという見方があります。つまり、回転行列を
\begin{pmatrix}
C_{11} & C_{12} & C_{13} \\
C_{21} & C_{22} & C_{23} \\
C_{31} & C_{32} & C_{33}
\end{pmatrix}
として、回転前の座標系 (基準座標系) の基底ベクトルを $\vec{e_x}, \vec{e_y}, \vec{e_z}$ としたとき、回転後の座標系 (機体座標系) の基底ベクトル $\vec{b_x}, \vec{b_y}, \vec{b_z}$ としたとき、
\begin{align}
\vec{b_x} &= C_{11} \vec{e_x} + C_{21} \vec{e_y} + C_{31} \vec{e_z} \\
\vec{b_y} &= C_{12} \vec{e_x} + C_{22} \vec{e_y} + C_{32} \vec{e_z} \\
\vec{b_z} &= C_{13} \vec{e_x} + C_{23} \vec{e_y} + C_{33} \vec{e_z} \end{align}
という関係が成り立つので、
(\vec{b_x} \vec{b_y} \vec{b_z}) = (\vec{e_x} \vec{e_y} \vec{e_z})
\begin{pmatrix}
C_{11} & C_{12} & C_{13} \\
C_{21} & C_{22} & C_{23} \\
C_{31} & C_{32} & C_{33}
\end{pmatrix}
となります。つまり「基準座標系から機体座標系への基底変換行列」は回転行列そのものとなっています。回転行列を基底変換行列とみなすことのメリットとしては、あるベクトルの成分が、基準座標系で記述された成分値 $(x_i, y_i, z_i)$ と、機体座標系で記述された成分値 $(x_b, y_b, z_b)$ で与えられていたときに
\begin{pmatrix}
x_i \\
y_i \\
z_i
\end{pmatrix}
=
\begin{pmatrix}
C_{11} & C_{12} & C_{13} \\
C_{21} & C_{22} & C_{23} \\
C_{31} & C_{32} & C_{33}
\end{pmatrix}
\begin{pmatrix}
x_b \\
y_b \\
z_b
\end{pmatrix}
という関係性が得られることが挙げられます (線型代数学で学ぶ内容がここで活きます)。これにより、「宇宙機において何個かの星についての、星カタログの情報 (基準座標系) とスターセンサの情報 (機体座標系) とから、宇宙機の姿勢状態を推定する」といったシンプルかつ重要な応用ができるようになります。理論上は 2 個の星についての情報があれば、DCM を復元することができます。
3. そもそもクォータニオンとは
近年クォータニオンに対しては
- 数学的なもので実体がよくわからない
- 別に内部の数学を知っている必要はなく、使い方がわかっていればいい
という風潮が強いと感じています。しかし中身がよくわからないものを扱うことに居心地の悪さを感じる方も多いのではないでしょうか。クォータニオンの数学は難しいと思い込んでいる方も多いですが、実際はとても単純明快なものです。本節ではクォータニオンの中身に興味のある方向けにクォータニオンの実体を紹介したいと思います。
3-1. クォータニオンの実体
クォータニオンとはそもそも何なのか、モヤモヤした気持ちを抱いている方も多いと思いますが、実体は四次元ベクトルだと思って差し支えないです。ただし以下の点で特別な四次元ベクトルになっています。
クォータニオン同士の掛け算ができて、掛け算した結果もクォータニオンになる
普通のベクトル同士も足し算、引き算はできますが、掛け算は一般には定義できないです。掛け算っぽいものとして「内積」はありますが、内積は掛け算した結果がベクトルではなくスカラーになるので、また少し違うものです。三次元ベクトルに限っては「外積」があります。実は外積とクォータニオンの掛け算には密接な関係があります。クォータニオンの第四成分を 0 にしたもの同士の掛け算は、三次元ベクトルの外積とぴったり対応します (その話題について興味のある方は「七次元の外積」を読むと面白いです)。
さて、しかもクォータニオンに定義された掛け算はただの掛け算ではないのです!すごいことに、
- クォータニオン $q_1$ で表される回転
- クォータニオン $q_2$ で表される回転
を立て続けに実行する操作は、それ自体 1 つの回転とみなせるわけですが、それはクォータニオン $q_2q_1$ で表される回転になっているわけです。この性質があるために、クォータニオンはとても便利に活用することができます。クォータニオンを用いた回転の合成が容易なのも、補間ができるのも、シミュレーション計算ができるのも、元はと言えばこの性質に依っています。
3-2. 複素数の拡張としてのクォータニオン
クォータニオンの数学的側面について解説した資料では、必ずと言っていいほど最初に複素数が登場します。クォータニオンは日本語では四元数であり、複素数の拡張になっています。
- 二次元平面内での回転は、2 × 2 行列でも、複素数 (複素平面) でもできる
- 三次元空間内での回転は、3 × 3 行列でできる
...となると、複素数の三次元空間内回転バージョンを考えたくなります。それが四元数だというストーリーです。ハミルトンはまさにこの問題に精魂を注ぎ込み、一生を捧げる貢献をしました。
余談なのですが、高校数学ではしばしば「行列」と「複素数平面」はどちらかが指導要領に採用されるとどちらかが削られる傾向にあります。上記のストーリーを考えると少し微妙な気持ちになることがあります。確かに行列も複素数平面も「二次元平面内の回転を扱える」という点で共通しているので、どちらかを教えればいいという考えもわかるのですが、同じ事柄を実現する複数のものを学ぶことによって見えて来る世界もあると思うのです。
さて、複素数は 2 個の実数 $x, y$ を用いて $x + yi$ と表される数であり、これは二次元実数ベクトル $(x, y)$ ともみなせます。同様に四元数は 4 個の実数 $x, y, z, w$ を用いて $w + xi + yj + zk$ と表される数であり、四次元実数ベクトル $(x, y, z, w)$ ともみなせます。というわけで、クォータニオンは特別な四次元ベクトルになっています。整理すると以下のような感じです。
||対応ベクトル|実現する回転|回転行列|
|---|---|---|---|---|
|実数 $x$|一次元ベクトル $(x)$|-|1 × 1 行列|
|複素数 $x + yi$|二次元ベクトル $(x, y)$|二次元回転|2 × 2 行列|
|四元数 $w + xi + yj + zk$|四次元ベクトル $(x, y, z, w)$|三次元回転|3 × 3 行列|
注意点として、三次元回転を表すクォータニオンは特にノルムが $1$ である必要がありますし、逆にノルムが $1$ のクォータニオンは特に回転を表すものになっています。思えば複素平面上での回転を表す複素数も、ノルム (絶対値) が $1$ である必要がありました。
クォータニオン (四元数) 自体にはノルムが $1$ という制約はないですが、航空宇宙や 3D ゲームの文脈で言及されるクォータニオンは暗黙にノルムが $1$ であることを課しており、特にノルムが $1$ のクォータニオンのことをクォータニオンと呼んでいる感じです。
3-3. 四元数のかけ算
複素数のかけ算は
$$i^2 = -1$$
によって残りは分配法則によって決まりました。すなわち
\begin{align}
(a + bi)(c + di) &= ac + adi + bci - bd \\
&= (ac - bd) + (ad + bc)i
\end{align}
です。四元数では単位が $i, j, k$ と 3 つあるので、これらすべての、$3 × 3 = 9$ 通りの組合せのかけ算を決めてあげます。色んなことが考えられるかもしれませんが
$$i^2 = j^2 = k^2 = ijk = -1$$
だけ決めるとあとはすべて自動的に決まってしまいます。例えば $ijk = -1$ の両辺に左から $i$ をかけると、$-jk = -i$ となって、$jk = i$ であることが決まります。この調子で行くと
| $i$ | $j$ | $k$ | |
|---|---|---|---|
| $i$ | $-1$ | $k$ | $-j$ |
| $j$ | $-k$ | $-1$ | $i$ |
| $k$ | $j$ | $-i$ | $-1$ |
と求まります。注意点として、複素数では成り立った交換法則が、四元数では成り立ちません。現に $ij = k$ ですが $ji = -k$ となっていて $ij \neq ji$ です。
そしてこの表が決まると、一般の四元数のかけ算も分配法則で計算できます。実際にやってみると「1-4. クォータニオンのかけ算」で登場したかけ算と完全に一致することがわかります。
さて、いくつか四元数に関する定義を行い、様々な性質を紹介します。まず
- 四元数 $q$ のノルム: $|q| = \sqrt{q_w^2 + q_x^2 + q_y^2 + q_z^2}$
- 四元数 $q$ の共役四元数: $\bar{q} = q_w - q_xi - q_yj - q_zk$
- 四元数 $q$ の逆数: $q^{-1} = \frac{\bar{q}}{|q|^2}$
であり、$qq^{-1} = q^{-1}q = 1$ が成立します。特に三次元回転を表すクォータニオンは $|q| = 1$ であるため、$q^{-1} = \bar{q}$ となります。つまり共役四元数が逆回転を表しています。
四元数の重要な性質の 1 つは「体」であること、すなわち逆数が定義できて割り算もできることでしょう。逆にそうなるように最初に
$$i^2 = j^2 = k^2 = ijk = -1$$
と決めた感じです。実は $a + bi + cj + dk + ...$ ($a, b, c, d, ...$ は実数) の形で体となるものは、「実数」「複素数」「四元数」の 3 通りしかないことが知られています。注意点として、四元数体は実数体や複素数体と異なり掛け算の交換法則が成り立たないです。数学的にはそのようなものは斜体と呼ぶことが多いです。
3-4. クォータニオンから回転行列への準同型性
前に「三次元回転行列がもつ性質を失わずに 4 個のパラメータに圧縮したものがクォータニオンである」と書きました。そのことを深掘りします。
| 回転させるもの | 回転結果 | 備考 |
|---|---|---|
| ベクトル $\vec{v}$ | $q \vec{v} \bar{q}$ | $\bar{q}$ は $q$ の逆回転 |
| 姿勢クォータニオン $p$ | $qp$ |
というのがほぼすべてなのですが、これを考えていきます。
その前にノルムが $1$ の複素数 $z = x + yi$ は二次元回転を表していましたが、対応する 2 × 2 行列を $T(z)$ と書くことにすると
T(z) =
\begin{pmatrix}
x & -y \\
y & x
\end{pmatrix}
です。そして 2 つの複素数 $z_1, z_2$ に対して
T(z_2 z_1) = T(z_2)T(z_1)
が成り立っていました。これはすなわち、複素数のかけ算がそのまま 2 回回転に対応していることを示しています。
一般に 2 つの群 $G, G'$ に対して写像 $f: G \to G'$ があって任意の $x, y \in G$ に対して
$$f(xy) = f(x)f(y)$$
を満たすとき、$f$ を準同型写像と呼び、$G$ と $G'$ は準同型な関係で結ばれているいうことになります。これはすなわち $G$ と $G'$ がかけ算の意味では本質的に同じ構造を持っていることを意味しています。ノルム 1 の複素数から、二次元回転行列に対して、準同型写像があります。
この準同型性がそのまま、ノルム 1 のクォータニオンから、三次元回転行列に対しても成立します!これこそがクォータニオンのよい性質の根底にあるものです。クォータニオンのかけ算がちょうどピッタリ 2 回回転に対応しているのです。
大変な計算になるのですが、
- ベクトル $\vec{v}$ をクォータニオン $q$ によって回転したものは $q\vec{v}\bar{q}$ になること
- 下で定義される行列を $T(q)$ として、$T(q_2q_1) = T(q_2)T(q_1)$ が成り立つこと
は計算によって確かめることができます。
\begin{pmatrix}
q_x^2-q_y^2-q_z^2+q_w^2 & 2(q_xq_y-q_zq_w) & 2(q_xq_z+q_yq_w) \\
2(q_xq_y+q_zq_w) & -q_x^2+q_y^2-q_z^2+q_w^2 & 2(q_yq_z-q_xq_w) \\
2(q_xq_z-q_yq_w) & 2(q_yq_z+q_xq_w) & -q_x^2-q_y^2+q_z^2+q_w^2
\end{pmatrix}
このうち前者についてはこの記事に具体的な計算があるので参考にしてもらえたらと思います。そして実は後者については、前者の計算が確かめられていたら証明は簡単です。ベクトル $\vec{v}$ に対してまずクォータニオン $q_1$ な回転をしてクォータニオン $q_2$ な回転をして得られるベクトルは、
$$q_2(q_1 \vec{v} \bar{q_1})\bar{q_2} = (q_2 q_1) \vec{v} (\overline{q_2q_1})$$
になりますが、これはよく見るとベクトル $\vec{v}$ にクォータニオン $q_2q_1$ な回転をしたものになっています。すなわち任意のベクトル $\vec{v}$ に対して、
- クォータニオン $q_1$ な回転をして
- クォータニオン $q_2$ な回転
をしたものと
- クォータニオン $q_2q_1$ な回転
をしたものが一致することになります。よって $T(q_2q_1) = T(q_2)T(q_1)$ は成立します。
4. おわりに
本記事ではクォータニオンについて、基礎的なところから数理的なところまで総合的に整理してみました。クォータニオンについて個人的に思うこととして、航空宇宙業界、ロボティクス、3D ゲーム業界...と分野横断的に使われているところにとても魅力を感じています。
クォータニオンに限らず、僕は様々な分野で横断的に活用できる数理工学手法が大好きです。人工知能、レコメンド、シフトスケジューリング、金融、生産計画、物流... と幅広く活用できる数理最適化などはまさにその典型例と言えますし、機械学習や数値解析なども多岐にわたる分野で活躍しています (下図は 講義資料 より引用)。
本記事の隠れたテーマとして「扱いたい対象の背後にある数理をきちんと学べば様々な場面で応用が利くことの一例を示したい」という気持ちがありました。それが少しでも伝わったならばとても嬉しい気持ちです。