はじめに
カルマンフィルタといったら一般的に線形カルマンフィルタのことを指すが、この線形カルマンフィルタは線形システムのモデルにしか適用できない。
そこで、この線形カルマンフィルタを非線形モデルに適用できるよう拡張されたのが拡張カルマンフィルタ(Extended Kalman Filter, EKF)となります。
拡張カルマンフィルタ(Extended Kalman Filter)
線形カルマンフィルタの場合、状態空間モデルは以下の式で表されていました。
- 状態空間モデル(線形)
\begin{align}
\boldsymbol{x}(k+1) &= \boldsymbol{A} \boldsymbol{x}(k) +
\boldsymbol{B} \boldsymbol{u}(k) + \boldsymbol{v}(k) \tag{1}\\
\boldsymbol{y}(k) &= \boldsymbol{C} \boldsymbol{x}(k) + \boldsymbol{w}(k) \tag{2}\\
\end{align}
なお、線形カルマンフィルタの詳細については前回の記事を参考にしてください。
・SLAM(Simultaneous Localization and Mapping)と環境計測センサについて
拡張カルマンフィルタの場合、状態空間モデルは以下の式で表わされます。
- 状態空間モデル(非線形)
\begin{align}
\boldsymbol{x}(k+1) &= \boldsymbol{f}(\boldsymbol{x}(k), \boldsymbol{u}(k)) + \boldsymbol{v}(k) \tag{3}\\
\boldsymbol{y}(k) &= \boldsymbol{h}(\boldsymbol{x}(k)) + \boldsymbol{w}(k) \tag{4}\\
\end{align}
但し、
$\boldsymbol{f}(\cdot)$:$\boldsymbol{x}(k)$及び、$\boldsymbol{u}(k)$の非線形関数
$\boldsymbol{h}(\cdot)$:$\boldsymbol{x}(k)$の非線形関数
$\boldsymbol{f}(\cdot)$と$\boldsymbol{h}(\cdot)$は、どちらの非線形関数であるため、直接共分散行列を計算することができません。しかし、これらの関数を線形近似することによって線形カルマンフィルタと同じ要領で解くことができます。線形システムと非線形システムは対立する関係ではなく、非線形システムの特殊な場合が線形システムであるととらえることが重要です。
拡張カルマンフィルタでは非線形の状態方程式と観測方程式の偏微分行列(ヤコビアン)を用います。
\begin{align}
\boldsymbol{A}(k) &= \left.\frac{\partial \boldsymbol{f}(\boldsymbol{x}, \boldsymbol{u})}{\partial \boldsymbol{x}}\right|_{\boldsymbol{x}=\boldsymbol{\hat{x}}(k), \boldsymbol{u}=\boldsymbol{u}(k)} \tag{5}\\
\boldsymbol{C}(k) &= \left.\frac{\partial \boldsymbol{h}(\boldsymbol{x})}{\partial \boldsymbol{x}}\right|_{\boldsymbol{x}=\boldsymbol{\hat{x}}(k)} \tag{6}\\
\end{align}
この場合のカルマンフィルタの時間更新式は次のようになります。
- 予測ステップ
\begin{align}
事前状態推定値&: \boldsymbol{\hat{x}}^-(k) = \boldsymbol{f}(\boldsymbol{\hat{x}}(k-1), \boldsymbol{u}(k-1)) \tag{7}\\
線形近似&: \boldsymbol{A}(k-1) = \left.\frac{\partial \boldsymbol{f}(\boldsymbol{x}, \boldsymbol{u})}{\partial \boldsymbol{x}}\right|_{\boldsymbol{x}=\boldsymbol{\hat{x}}(k-1), \boldsymbol{u}=\boldsymbol{u}(k-1)} \tag{8}\\
& \boldsymbol{C}(k) = \left.\frac{\partial \boldsymbol{h}(\boldsymbol{x})}{\partial \boldsymbol{x}}\right|_{\boldsymbol{x}=\boldsymbol{\hat{x}}(k)} \tag{9}\\
事前誤差共分散行列&: \boldsymbol{P}^-(k) = \boldsymbol{A}(k-1) \boldsymbol{P}(k-1) \boldsymbol{A}^T(k-1) + \boldsymbol{Q}(k-1) \tag{10}\\
\end{align}
- フィルタリングステップ
\begin{align}
カルマンゲイン行列&: \boldsymbol{G}(k) = \boldsymbol{P}^-(k) \boldsymbol{C}^T(k) (\boldsymbol{C}(k) \boldsymbol{P}^-(k) \boldsymbol{C}^T(k) + \boldsymbol{R}(k))^{-1} \tag{11}\\
状態推定値&: \boldsymbol{\hat{x}}(k) = \boldsymbol{\hat{x}}^-(k) + \boldsymbol{G}(k)(\boldsymbol{y}(k) - \boldsymbol{h} (\boldsymbol{\hat{x}}^-(k)) \tag{12}\\
事後誤差共分散行列&: \boldsymbol{P}(k) = (\boldsymbol{I} - \boldsymbol{G}(k) \boldsymbol{C}) \boldsymbol{P}^-(k) \tag{13}\\
\end{align}
例題
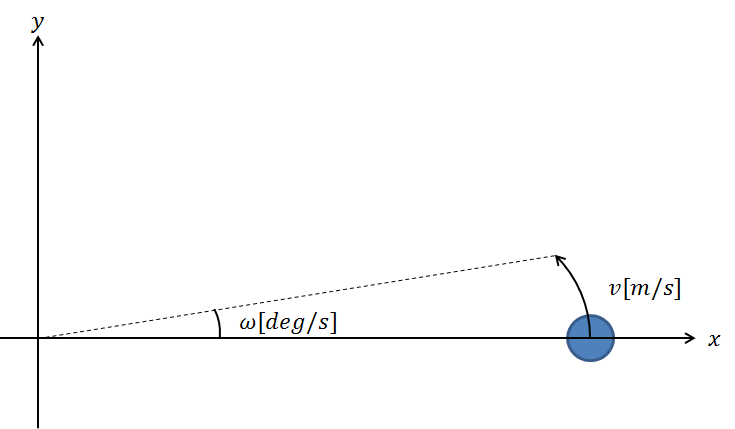
2次元座標において、あるロボットが速度$v[m/s]$、角速度$\omega[deg/s]$で周回移動するものとします。このとき、ロボットの移動には誤差$\boldsymbol{v}(k)$を含みます。また、ロボットの位置を観測するセンサも誤差$\boldsymbol{w}(k)$を含みます。サンプリング周期は$\Delta t$とします。ここで、観測された軌跡から実際の軌跡を拡張カルマンフィルタによって推定します。
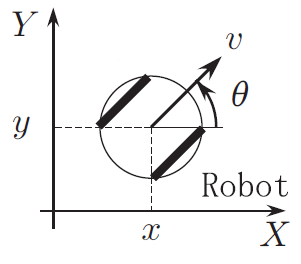
ここで、ロボットの姿勢を定義します。
$x,y,\theta$はそれぞれ、ロボットの$X$座標、$Y$座標、姿勢角を表し、姿勢ベクトル$\boldsymbol{x}(k)$は以下のように定義されます。
\boldsymbol{x}(k) =
\begin{bmatrix}
x(k) \\
y(k) \\
\theta(k) \\
\end{bmatrix} \tag{14}\\
よって状態方程式は以下のようになります。
\begin{align}
\boldsymbol{\hat{x}}^-(k+1) &= \boldsymbol{f}(\boldsymbol{\hat{x}}(k),\boldsymbol{u}(k)) \\
&=
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
\boldsymbol{\hat{x}}^-(k)
+
\begin{bmatrix}
v & 0 & 0 \\
0 & v & 0 \\
0 & 0 & \omega \\
\end{bmatrix}
\boldsymbol{u}(k) \\
\end{align} \tag{15}\\
但し、
\boldsymbol{u}(k) = \begin{bmatrix}
\Delta t \cdot cos\theta(k) \\
\Delta t \cdot sin\theta(k) \\
\Delta t \\
\end{bmatrix} \tag{16}\\
するとヤコビアンは以下のように求められます。
\frac{\partial \boldsymbol{f}(\boldsymbol{x}, \boldsymbol{u})}{\partial \boldsymbol{x}} =
\begin{bmatrix}
1 & 0 & v \cdot \Delta t \cdot cos\theta(k) \\
0 & 1 & v \cdot \Delta t \cdot sin\theta(k) \\
0 & 0 & 1 \\
\end{bmatrix}
\tag{17}\\
次は観測値$\boldsymbol{y}(k)$を定義します。
まず、観測ベクトル$\boldsymbol{y}(k)$を以下のように定義します。
\boldsymbol{y}(k) =
\begin{bmatrix}
x(k) \\
y(k) \\
\end{bmatrix} \tag{18}\\
$x,y$はそれぞれ、観測されたロボットの$X$座標、$Y$座標を表します。
次に、観測値$\boldsymbol{y}(k)$は「真の位置$\boldsymbol{x}_{gt}(k)$+観測雑音$\boldsymbol{w}(k)$」で与えられるものとします。そうすると、観測値は以下の式で算出されます。
\boldsymbol{y}(k) =
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
\end{bmatrix}
\boldsymbol{x}_{gt}(k)
+ \boldsymbol{w}(k)
\tag{19}\\
例題の説明は以上です。
上記例題を実装したスクリプトはGitHubで公開しています。
・GitHub - extended_kalman_filter.py
また、スクリプトを実行した結果は以下のようになります。
(画像をクリックするとYouTubeへジャンプします。)
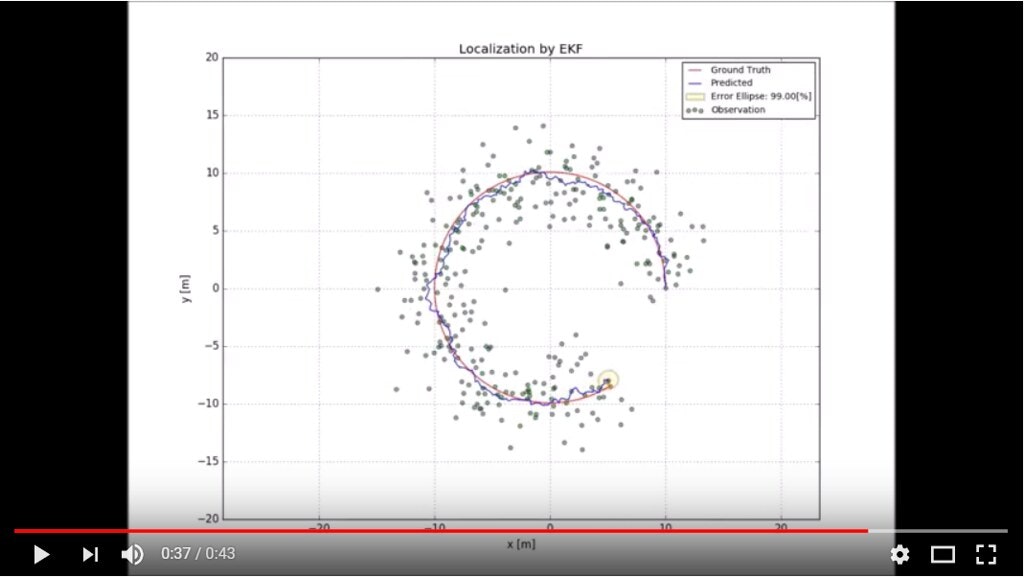
青い点が拡張カルマンフィルタによる推定値になるのですが、その回りに見える黄色の薄い楕円は誤差楕円(Error Ellipse)となっています。
上記誤差楕円を含め、スクリプトを書く際は以下のサイトを参考にさせていただきました。
・拡張カルマンフィルタを使用した自己位置推定MATLABサンプルプログラム
・カルマンフィルタにおける誤差楕円の計算方法
先駆者に感謝します。
おわりに
次はパーティクルフィルタやろうかな・・・