はじめに
皆さん、SLAMというものをご存知でしょうか?SLAM(Simultaneous Localization and Mapping)とは自己位置推定と環境地図作成を同時に行う今流行?の技術です。最近よく耳にする自動運転システムもこのSLAMという技術を用いているらしいです。
環境計測センサ
自己位置推定は与えられた環境地図上で自分自身がが今、どこにいて、そしてどのような姿勢をしているのかをセンサデータより推定することです。(環境地図が与えられていない場合もありますが、ここでは与えられていることを前提で話します。)
自己位置推定には、一般的に以下のセンサが使用されます。
GPS
GPSとは上空にある数個の衛星からの信号をGPS受信機で受け取り、受信者が自身の現在位置を知るシステムです。GPSを利用して計測を行う上での最大の利点は、基線なしに基準点を計測できることです。よって屋外のような開けた場所では非常に有効です。しかし、欠点そして樹木や建物などの遮蔽物が多く存在する環境ではGPS信号を補足することが困難となり、自己位置推定の精度が大きく低下する場合があります。

距離測定センサ
距離測定センサには以下のようなものがある。
カメラ
カメラを使った距離計測センサには大きく分けて以下の2つがある。一般的にカメラを使った距離計測の利点は画像という視覚情報(Red/Green/Blue) + 距離情報(Depth)が取得できることにある。よって距離を計測しながらテクスチャの解析(道路の白線検地や標識認識など)を行うことができる。
-
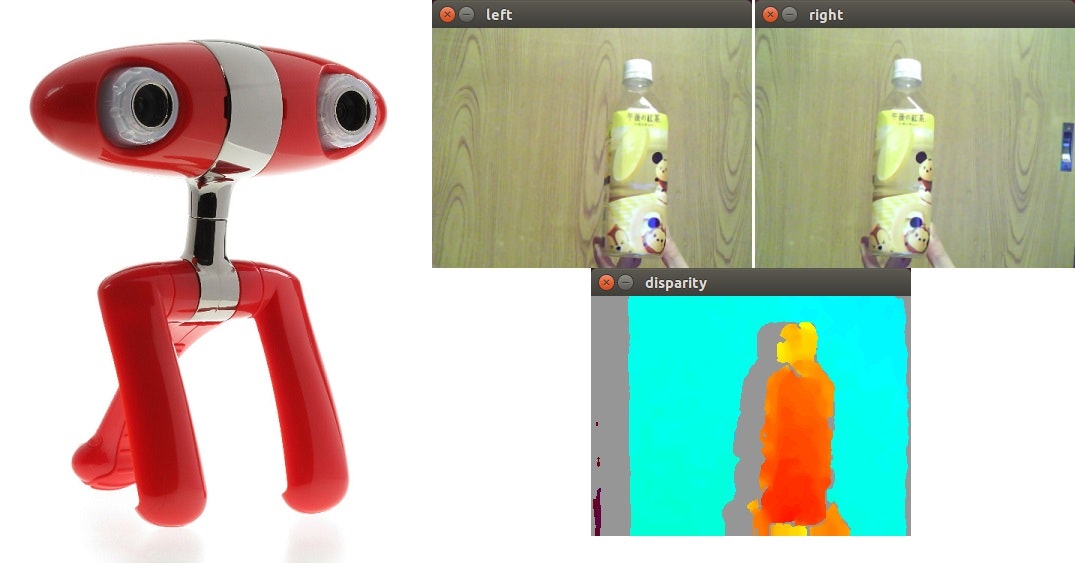
ステレオカメラ
単に2台のカメラを並列に並べたカメラセンサです。2台のカメラで画像を同時に2枚取得し、両画像間の視差から三角測量によって距離を算出することができます。一方の画像のある1ピクセルに対応するピクセル点をもう一方の画像上から探索する必要があり、この作業をステレオマッチングと呼ぶ。このステレオマッチングはテクスチャ情報を基に探索する必要があり、その分の計算コストも必要になりまた、対応点を正確に探索できなかった場合は著しく測定精度が下がってしまうような欠点がある。
取得された画素数にもよるが、一般的にステレオマッチングはかなりの計算コストを要することからGPUやFPGA等のステレオマッチング専用のハードウエアを使わないと実用に耐えない気がします。
-
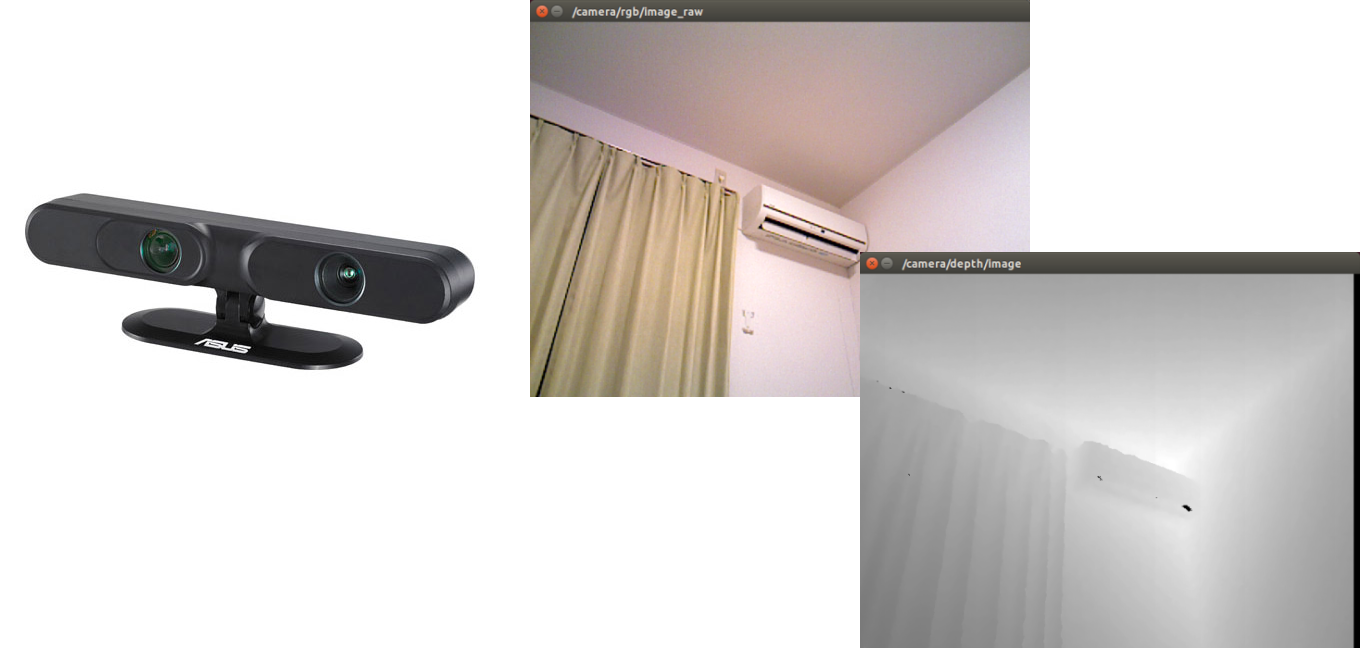
デプスカメラ
30Hz~60Hz程度のパルスで投影された赤外線をカメラで読み取り、光が往復した時間から距離を算出するセンサです。この算出方法はToF(Time of Flight)とも呼ばれ、Kinect v2にも搭載されています。(Kinect v1はToFではないようです。)カラー画像の取得と距離を同時に取得できることからRGBDカメラとも呼ばれます。
ステレオカメラと同等の情報が得られますが、こちらの利点はステレオカメラに比べ、計算コストが小さく、画像処理専用のハードウエアを使用しなくてもリアルタイム性を十分確保できることにある。欠点として、日光の当たる屋外や、赤外線の反射率が極めて高い鏡や金属、吸収率が極めて高い黒色の物体のように、赤外線をカメラで読み取ることができないような環境では計測不可となってしまうことである。
レーザーレンジファインダ(LRF)
レーザーレンジファインダ(LRF)とは、赤外線レーザーを発振してそれを目標物に照射、その反射の度合いで目標物までの距離を一瞬で測定出来るという光学機器です。一瞬で測定できるため、リアルタイム性はかなり高いですが、環境の1平面分しか測定できないため、カメラに比べ、取得できる情報が少ないという欠点があります。

オドメトリ
車やロボットに取り付けられた車輪の回転量から位置を推定する手法です。デッドレコニングともいいます。エンコーダをジャイロなどのセンサ情報を足し合わせて、逐次自身の位置と姿勢を算出していきます。カーナビにも搭載されているらしく、GPSが取得できないトンネル内等でも自身の位置を正確に推定できるのはこのオドメトリのおかげらしいです。

自己位置推定
上記のセンサを用いて得られた測定結果を統合し、自己位置同定することでより精度の高い自己位置推定を行うことができると考えられます。自己位置推定の技術の一般的な方法にはカルマンフィルタがあります。
カルマンフィルタ
カルマンフィルター(Kalman filter)は、誤差のある観測値を用いて、ある動的システムの状態を推定あるいは制御するための、無限インパルス応答フィルターの一種です。
もっと詳細を知りたい方は以下で非常に分かりやすく書かれているので参考にしてみるとよい。
カルマンフィルタの目的は、時刻$k$において、雑音の混入した時系列データ$y(k)$が観測されたとき、その背後にある物理量(状態)を、その時刻において利用可能な観測データ $\{y(k), i=1,2,...,k\}$ と時系列の状態空間モデルを用いることによって推定することです。
- 状態空間モデル
\begin{align}
\boldsymbol{x}(k+1) &= \boldsymbol{A} \boldsymbol{x}(k) +
\boldsymbol{B} \boldsymbol{u}(k) + \boldsymbol{v}(k) \tag{1}\\
\boldsymbol{y}(k) &= \boldsymbol{C} \boldsymbol{x}(k) + \boldsymbol{w}(k) \tag{2}\\
\end{align}
但し、
$\boldsymbol{x}(k)$:$n$次元状態ベクトル
$\boldsymbol{y}(k)$:$p$次元観測ベクトル
$\boldsymbol{u}(k)$:$r$次元制御入力ベクトル
$\boldsymbol{v}(k)$:平均ベクトル$0$、共分散行列$\boldsymbol{Q}$の$n$次元システム雑音ベクトル
$\boldsymbol{w}(k)$:平均ベクトル$0$、共分散行列$\boldsymbol{R}$の$p$次元観測雑音ベクトル
$\boldsymbol{A}$:$n \times n$状態遷移行列
$\boldsymbol{B}$:$n \times r$制御行列
$\boldsymbol{C}$:$p \times n$観測行列
このとき、カルマンフィルタの時間更新式は次のようになります。
- 予測ステップ
\begin{align}
事前状態推定値&: \boldsymbol{\hat{x}}^-(k) = \boldsymbol{A} \boldsymbol{\hat{x}}(k-1) + \boldsymbol{B} \boldsymbol{u}(k-1) \tag{3}\\
事前誤差共分散行列&: \boldsymbol{P}^-(k) = \boldsymbol{A} \boldsymbol{P}(k-1) \boldsymbol{A}^T + \boldsymbol{Q} \tag{4}\\
\end{align}
- フィルタリングステップ
\begin{align}
カルマンゲイン行列&: \boldsymbol{G}(k) = \boldsymbol{P}^-(k) \boldsymbol{C}^T (\boldsymbol{C} \boldsymbol{P}^-(k) \boldsymbol{C}^T + \boldsymbol{R})^{-1} \tag{5}\\
状態推定値&: \boldsymbol{\hat{x}}(k) = \boldsymbol{\hat{x}}^-(k) + \boldsymbol{G}(k)(\boldsymbol{y}(k) - \boldsymbol{C} \boldsymbol{\hat{x}}^-(k)) \tag{6}\\
事後誤差共分散行列&: \boldsymbol{P}(k) = (\boldsymbol{I} - \boldsymbol{G}(k) \boldsymbol{C}) \boldsymbol{P}^-(k) \tag{7}\\
\end{align}
カルマンフィルタでは、状態推定値を与える平均値(最尤推定値)$\boldsymbol{\hat{x}}(k)$だけでなく、状態推定値の精度を表す誤差共分散行列$\boldsymbol{P}(k)$も取得できることが一番の特徴になります。これによって、得られた状態推定値がどの程度信頼性があるものなのかを定量的に判断可能となります。
おわりに
カルマンフィルタといったら一般的に線形カルマンフィルタのことを指しますが、この線形カルマンフィルタは線形システムのモデルにしか適用できないという欠点があります。自動運転となると環境の変化や制御は当然非線形となり、線形カルマンフィルタを適用は困難となります。そこで次回、非線形システムを対象とした、「拡張カルマンフィルタ」についてお話ししたいと思います。