なんの記事?
Entity Linking 後編 に続く発展編です。
前回の実装までで、表層形を用いて候補を絞り込んだエンティティ・リンキングシステムを実装し、評価まで行いました。
本記事では、表層形による候補絞り込みを行わないエンティティリンキングモデルを実装します。
表層形を用いない候補探索の歴史
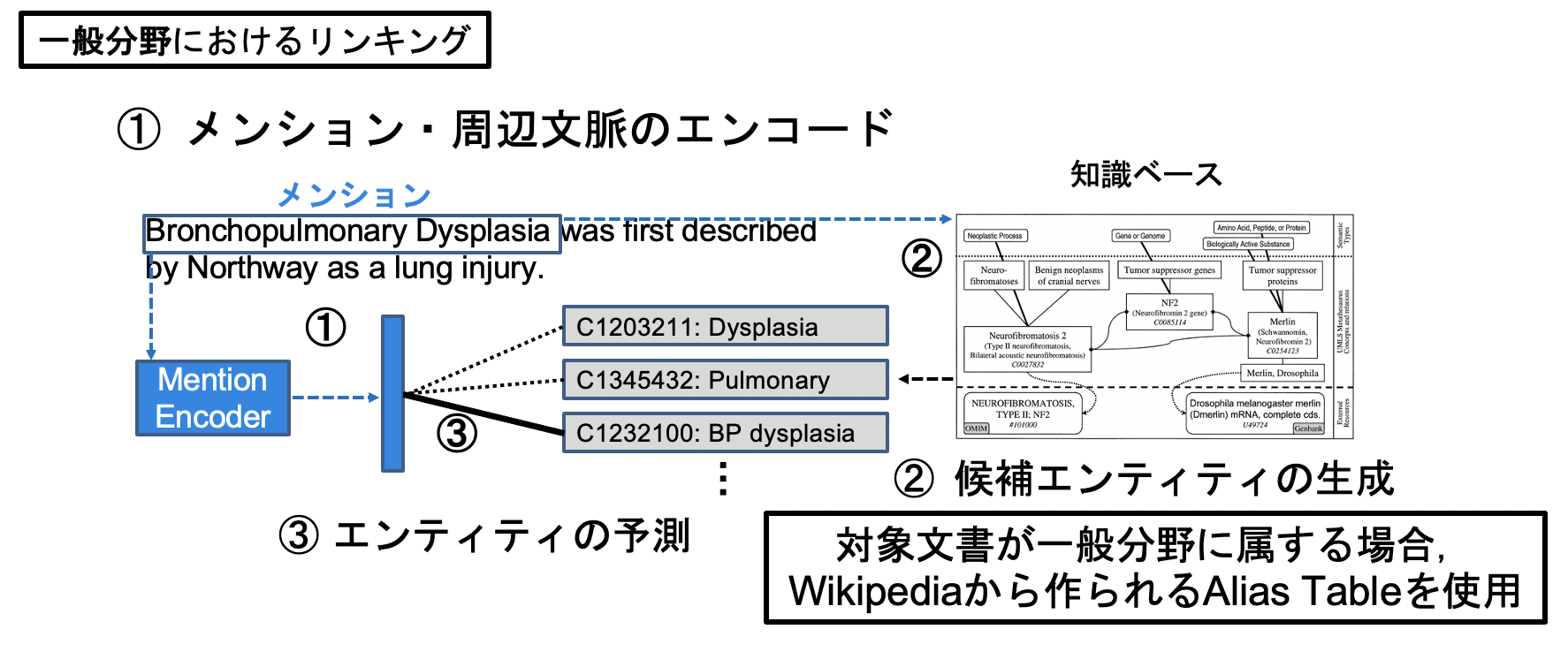
エンティティ・リンキング 前編 でも述べたように、エンティティ・リンキングではこれまで、表層形やWikipedia・Webコーパスの出現頻度情報を用いた候補生成を行い、残された候補からリンクエンティティを予測することが行われてきました。
このような情報を利用した候補生成は、Eshel et al., 2017; Gupta et al., 2017; Yamada et al., 2016; Ganea and Hofmann, 2017; Le and Titov, 2018; Cao et al., 2018 などで行われています。
事前に表層形や頻度情報を利用した候補生成を行うことで、真に予測すべきエンティティを予測する際の計算コストが、主なメリットです。
表層形を用いた候補生成のデメリット
ここで、表層形や頻度情報を用いた候補生成のデメリットを考えてみましょう。
頻度情報も含めて、メンションとエンティティの表層形そのものに候補生成が縛られている点が、デメリットになります。
具体例を通してみてみましょう。下記は、MedMentionsにおいて、表層形を用いた候補生成では、正解エンティティを生成出来なかった例になります。
MedMentionsは生物医学分野です。Wikipediaやウェブコーパスが扱うエンティティ全般は、一般ドメインと呼ぶことにしましょう。
一般ドメインに属するエンティティの場合、大量のウェブコーパスや、Wikipedia内の頻度情報・アンカーテキストから、充実した表層形辞書を作製することが可能です。
ところが、ドメインが限定された場合、一般ドメインと比してそのようなコーパスや頻度情報を確保することは難しいとされます。
加えて、メンションは文書中に多様な形で現れるので、それらすべてに対してルールを作製したり、候補辞書を用意することは更に難しくなります。
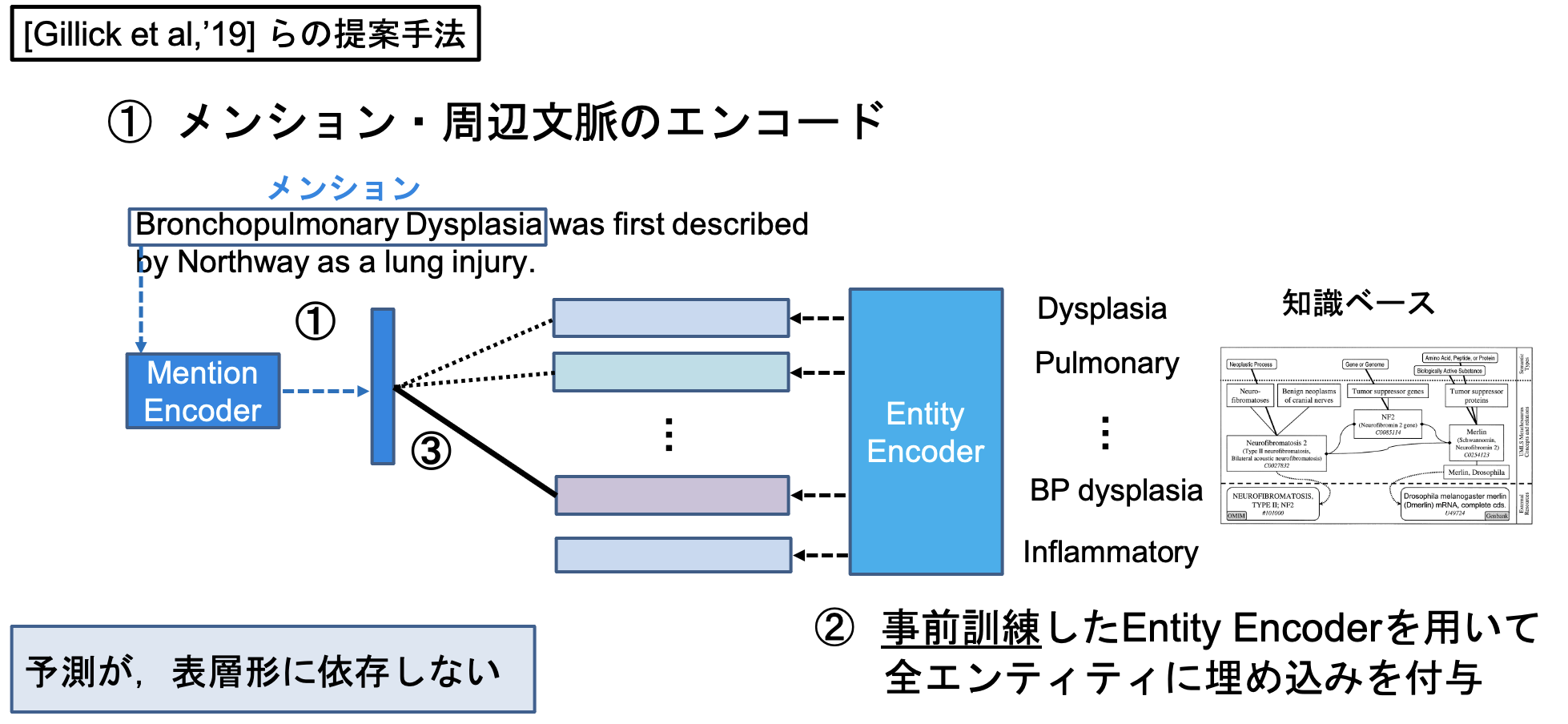
Bi-encoder構造 × 近似近傍探索 を用いたエンティティ・リンキング
そこで、表層形に縛られないメンションの候補エンティティ探索を考えます。手順は以下のようになります。
実際の論文では、エンコーダはBERTの先頭トークン、faissが近年では用いられます。今回もそれに従い、実装していきましょう。
とは言うものの、実装部分はほんの少しだけです。モデルについては前回までで実装が完了しており、
- 全entityに対する埋め込みの出力実装
- 埋め込みのfaissへの格納
- 評価部分
の実装のみになります。
実装
全entityに対する埋め込みの出力実装
ds = EntitiesInKBLoader(params)
entities = ds._read()
entity_ids = ds.get_entity_ids()
vocab = build_vocab(entities)
entity_loader = build_one_flag_loader(params, entities)
entity_loader.index_with(vocab)
predictor = KBEntityEmbEncoder(model, ds)
entity_idx2emb = {}
print('===Encoding All Entities from Fine-Tuned Entity Encoder===')
for entity_id in tqdm(entity_ids):
its_emb = predictor.predict(entity_id)['encoded_entities']
entity_idx2emb.update({entity_id: its_emb})
if params.debug and len(entity_idx2emb) == 300:
break
DatasetReaderを用いて知識ベース内全エンティティ用のリーダーを作製し、それをエンコーダに食わせるだけで終わります。
EntitiesInKBLoader の実装についてはソースコードを参照して下さい。
エンティティ埋め込みのfaissへの格納
自分が普段使いまわしているクラスをそのまま載せます。このクラスのインスタンスがそのまま、faissの探索エンジンになります。
import faiss
import numpy as np
class KBIndexerWithFaiss:
def __init__(self, config, entity_idx2emb, kbemb_dim=768):
self.config = config
self.kbemb_dim = kbemb_dim
self.article_num = len(entity_idx2emb)
self.entity_idx2emb = entity_idx2emb
self.search_method_for_faiss = self.config.search_method_for_faiss
self._indexed_faiss_loader()
self.KBmatrix, self.kb_idx2entity_idx = self._KBmatrixloader()
self._indexed_faiss_KBemb_adder(KBmatrix=self.KBmatrix)
def _KBmatrixloader(self):
KBemb = np.random.randn(self.article_num, self.kbemb_dim).astype('float32')
kb_idx2entity_idx = {}
for idx, (entity_idx, emb) in enumerate(self.entity_idx2emb.items()):
KBemb[idx] = emb
kb_idx2entity_idx.update({idx: entity_idx})
return KBemb, kb_idx2entity_idx
def _indexed_faiss_loader(self):
if self.search_method_for_faiss == 'indexflatl2': # L2
self.indexed_faiss = faiss.IndexFlatL2(self.kbemb_dim)
elif self.search_method_for_faiss == 'indexflatip': #
self.indexed_faiss = faiss.IndexFlatIP(self.kbemb_dim)
elif self.search_method_for_faiss == 'cossim': # innerdot * Beforehand-Normalization must be done.
self.indexed_faiss = faiss.IndexFlatIP(self.kbemb_dim)
def _indexed_faiss_KBemb_adder(self, KBmatrix):
if self.search_method_for_faiss == 'cossim':
KBemb_normalized_for_cossimonly = np.random.randn(self.article_num, self.kbemb_dim).astype('float32')
for idx, emb in enumerate(KBmatrix):
if np.linalg.norm(emb, ord=2, axis=0) != 0:
KBemb_normalized_for_cossimonly[idx] = emb / np.linalg.norm(emb, ord=2, axis=0)
self.indexed_faiss.add(KBemb_normalized_for_cossimonly)
else:
self.indexed_faiss.add(KBmatrix)
def _indexed_faiss_returner(self):
return self.indexed_faiss
インスタンスの中に kb_idx2entity_idx があります。実際のfaissの探索では、faissに格納された行列のインデックスが返されるため、このように faissのインデックス:実際のエンティティのインデックス を対応させる辞書が必要になります。
また、後の近似近傍探索でコサイン類似度を用いる場合は、事前の正規化が必要になります。こちらも注意しましょう。
def _indexed_faiss_KBemb_adder(self, KBmatrix):
if self.search_method_for_faiss == 'cossim':
KBemb_normalized_for_cossimonly = np.random.randn(self.article_num, self.kbemb_dim).astype('float32')
for idx, emb in enumerate(KBmatrix):
if np.linalg.norm(emb, ord=2, axis=0) != 0:
KBemb_normalized_for_cossimonly[idx] = emb / np.linalg.norm(emb, ord=2, axis=0)
self.indexed_faiss.add(KBemb_normalized_for_cossimonly)
else:
self.indexed_faiss.add(KBmatrix)
評価部分
探索部分
今回はモデルの中で、実際にfaissによる探索を行います。
contextualized_mention = self.mention_encoder(context)
distances, in_faiss_idxes = self.faiss_searcher.indexed_faiss.search(contextualized_mention.cpu().numpy(),
k=self.args.how_many_top_hits_preserved)
for mention_idx, in_faiss_candidates, gold_duidx_ in zip(mention_uniq_id.cpu().numpy(), in_faiss_idxes, gold_duidx.cpu().numpy()):
candidate_entity_idxes = [self.faiss_searcher.kb_idx2entity_idx[idx]
for idx in in_faiss_candidates]
self.mention_idx2candidate_entity_idxs.update({mention_idx:
{'candidate_entity_idx':candidate_entity_idxes,
'gold_entity_idx': gold_duidx_}})
モデルの中で別途 mention_idx2candidate_entity_idxs に、探索結果を保存しています。これ以外にも、モデルのアウトプット部分にメンションの埋め込みを入れておき外部で保存し、その後でfaissによる探索を行うやり方も考えられます。
評価部分
トップ候補のどの位置で含まれていたかを見る、Recall@X を用います。Recall@1だと本タスクでの正解率に相当します。
def candidate_recall_evaluator(dev_or_test: str, model, params, data_loader):
model.mention_idx2candidate_entity_idxs = copy.copy({})
evaluate(model=model, data_loader=data_loader, cuda_device=0, batch_weight_key="")
r1, r5, r10, r50 = 0, 0, 0, 0
for _, its_candidate_and_gold in model.mention_idx2candidate_entity_idxs.items():
candidate_entity_idxs = its_candidate_and_gold['candidate_entity_idx']
gold_idx = its_candidate_and_gold['gold_entity_idx']
if gold_idx in candidate_entity_idxs and candidate_entity_idxs.index(gold_idx) == 0:
r1 += 1
r5 += 1
r10 += 1
r50 += 1
continue
elif gold_idx in candidate_entity_idxs and candidate_entity_idxs.index(gold_idx) < 5:
r5 += 1
r10 += 1
r50 += 1
continue
elif gold_idx in candidate_entity_idxs and candidate_entity_idxs.index(gold_idx) < 10:
r10 += 1
r50 += 1
continue
elif gold_idx in candidate_entity_idxs and candidate_entity_idxs.index(gold_idx) < 50:
r50 += 1
continue
else:
continue
r1 = r1 / len(model.mention_idx2candidate_entity_idxs)
r5 = r5 / len(model.mention_idx2candidate_entity_idxs)
r10 = r10 / len(model.mention_idx2candidate_entity_idxs)
r50 = r50 / len(model.mention_idx2candidate_entity_idxs)
print('{}'.format(dev_or_test), 'evaluation result')
print('recall@{}'.format(params.how_many_top_hits_preserved), round(r50 * 100, 3), '%')
print('detail recall@1, @5, @10, @50',
round(r1 * 100, 3), '%', round(r5 * 100, 3), '%', round(r10 * 100, 3), '%', round(r50 * 100, 3), '%',
)
candidate_entity_idxs 内に正解エンティティがあればそのインデックスを参照し、最終的なリコールを算出しています。
実験結果
| Recall@X | 1 (Acc.) | 5 | 10 | 50 |
|---|---|---|---|---|
| dev_recall | 21.58 | 42.28 | 50.48 | 67.11 |
| test_recall | 21.50 | 40.29 | 47.95 | 64.52 |
今回は学習率以外とくに調整せず、このような結果となりました。
前回、テストデータでの正解率は68%だと報告しました。その数字と比べると、この数字は大きく劣るように一見見えます。
しかし、ここで重要であるのが、これらの数字はメンションとエンティティの表層形を一切使用しない候補探索によって出されたものであるということです。
今回使用したMeSHのエンティティ数は約29,054エンティティを含みます。
それぞれのメンションに対して、表層形を用いずエンコーダの出力のみを用いた探索を行い、約20%のメンションに対しては正解エンティティを30,000エンティティの中から見つけ出すことが出来ています。これは非常に驚異的です。
実際のBi-encoderを用いたエンティティ・リンキングでは、例えばGillick et al., '19 ではハイパーリンクを用いた約1億のアノテーションを用いています。
それに対して、今回用いた教師データは10,000で、Gillickらの10,000分の1に過ぎません。
まとめ
今回は、前回と異なり、メンションとエンティティの表層情報を一切用いないエンティティ・リンキングシステムを実装し、その評価を行いました。
実際のシステムでは、表層形での候補探索とBi-encoderによる候補探索をハイブリッドに用いることで、高い正解率やリコールを実現できる見込みがあることが分かりました。
ソースコード