\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
はじめに
様々な量子アルゴリズムの基礎となっている量子フーリエ変換($QFT$)と量子位相推定($QPE$)ですが、これらについて可視化しながら確認をしてみるという記事になります。
細かい部分については他の方々が詳しくかつ分かりやすく解説してくださっているので、そちらに譲ろうと思います。
QFTとQPEについて
QFTとQPEの概要
ここでまず、$QFT$と$QPE$が**何をやっているのか?**ですが、ざっくり言うと
- $QFT$:ある状態ベクトル$j$のスペクトル分解を量子回路で実現する
- $QPE$:あるユニタリ行列の$U$の固有値を量子回路によって近似的に求める
ということをしています。
この$QFT$と$QPE$の関係性ですが、$QPE$は$QFT$の逆操作である逆量子フーリエ変換($QFT^\dagger$)を使って位相推定を実現しています。
それだけなら古典の高速フーリエ変換($FFT$)だけで良いのでは?なぜわざわざ量子でやるの?と思われるかもしれませんが、$QFT$の優位性は計算量の観点にあります。
通常の$FFT$ではサンプル数$N$に対して$O(NlogN)$の計算量ですが、$QFT$は$n$個のqubitに対して$O(n^2)$となります。
ここで重ね合わせが活きているのですが、$n$個のqubitには$2^n$個のサンプルを埋め込むことが可能です。
なので、等価の比較をするのであれば、$FFT$の計算量$O(NlogN)$に対して$N=2^n$を適用することで以下の様に計算量を比較することができます。
FFT:O(n2^n)\\
QFT:O(n^2)
このように、圧倒的に$QFT$が計算量の観点で速い事がわかります。
ただし、いくら$QFT$であろうとも計算結果の観測に結局指数時間を要するので、全スペクトルを抽出するような用途ではなく、与えられた状態ベクトルのピークを求めるような用途で使うことで威力を発揮します。
そして位相キックバックを連鎖的に適用した結果に$QFT$の逆操作である$QFT^\dagger$をかけることで$QPE$を実現し、さらにこの$QPE$によって素因数分解や量子化学計算が実現できるのです。
そういうわけで、この2つのアルゴリズムは量子コンピュータの有用性を高める非常に重要なアルゴリズムなのです。
ちなみに位相キックバックを活用したアダマールテスト1でももちろん位相推定はできるのですが、アダマールテストでは測定用の量子ビットが1つなので、固有値が収束するまで何度か計算実行を繰り返してユニタリ行列の固有値を求めるような手順となってしまいます。
一方、$QPE$はアダマールテストの発展型とも言え、位相を誤差なく表現できるビット数の分の測定ビットを用意しさえすれば、精度良くユニタリ行列の固有値を求めることができます。
QFTとQFTの導出
以下が非常に分かりやすく解説されていますのでここで紹介させていただきます。
- $QFT$
- $QPE$
QFTを"見て"みる
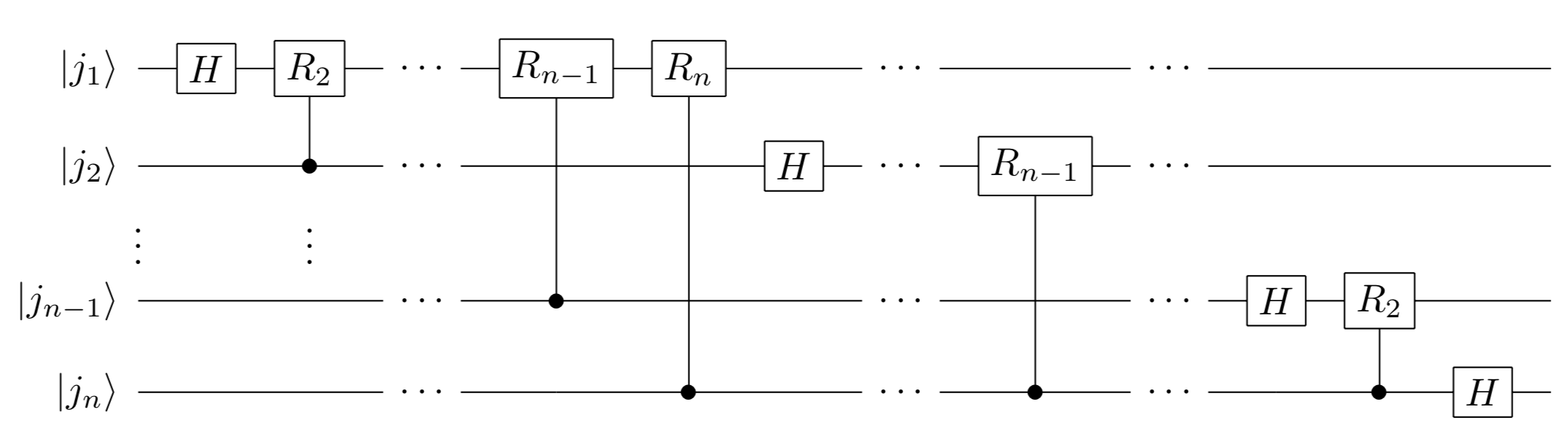
QFTの一般的な量子回路
入力される状態ベクトル $\ket{j}$ を $\ket{j_1...j_n}$ と表したとき、この入力に対するスペクトル分解を行う量子回路は次のように示されます。(スワップゲートは省略)
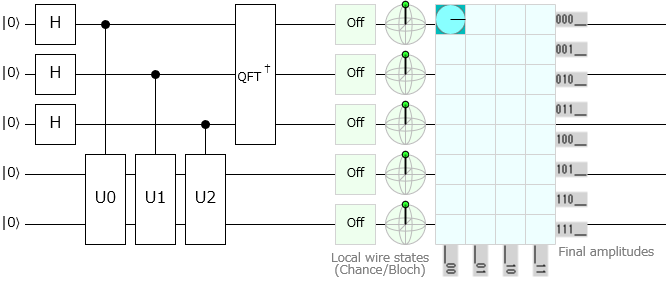
重ね合わせ状態を入力としたQFTを実行してみる
$QFT$に入力する状態ベクトルとして、3量子ビット全ての重ね合わせである
\ket{x} = \sum_{j=0}^7 \frac{1}{\sqrt{8}} \ket{j}
を入力すると本当に $\ket{000}$ が出力されるのかを確かめてみましょう。
確かに $\ket{000}$ が出力されており、フーリエ変換が正しくできていることが確認できました。
アニメーションで見てみる
8量子ビット、すなわち $2^8=256$個 の整数値に対して順番に$QPE$を実行した場合のアニメーションです。
入力と出力を見ると見事に入力ビットのON/OFFの動きが出力ビットの位相方向の動きに分解されて連動している様子がわかります。
QPEを"見て"みる
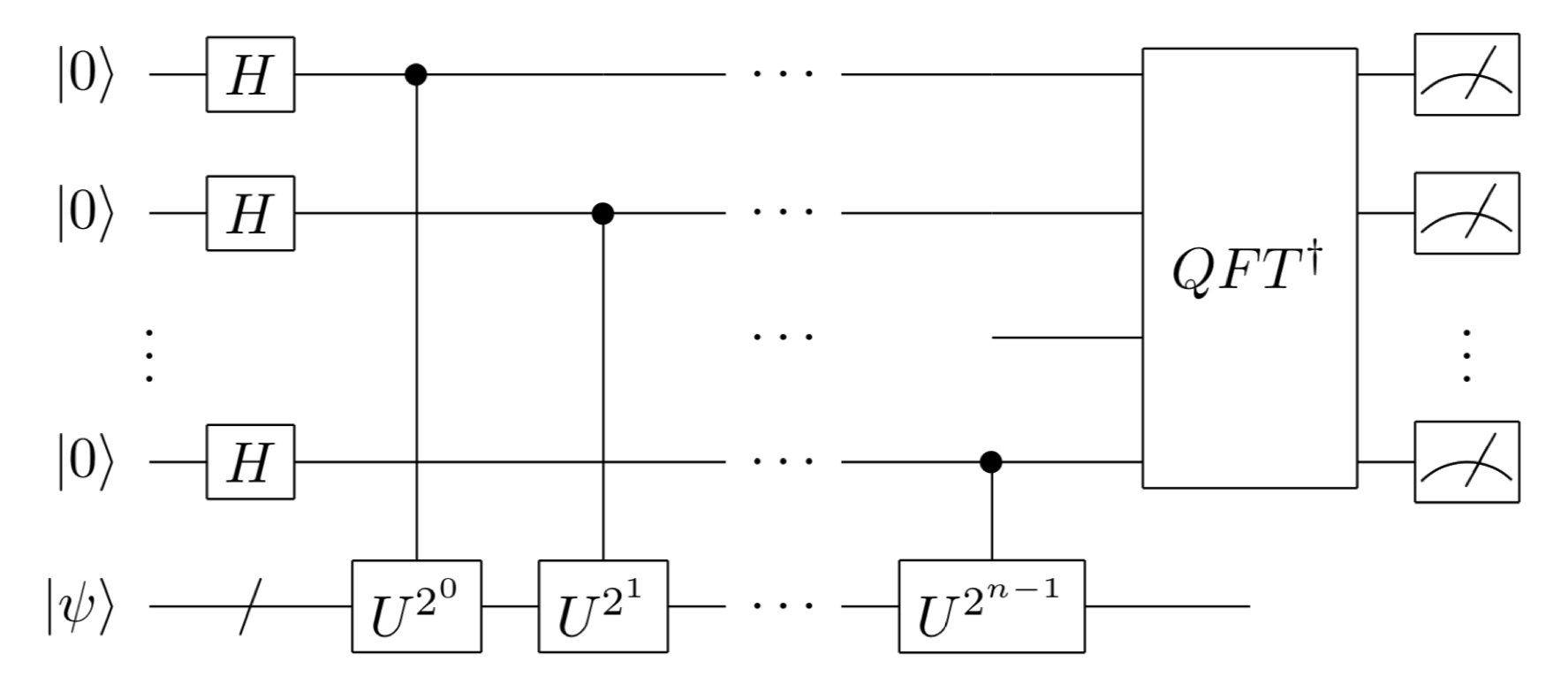
QPEの一般的な量子回路
アダマールテストでは測定用の量子ビットは1つでした1が、ここでは測定用の量子ビットを $n$ 個用意します。
その上で、あるユニタリ行列$U$の固有ベクトル $\ket{\psi}$ を入力したとき、$U$の固有値を求める量子回路は次のように示されます。
4x4のユニタリ行列に対してQPEを実行してみる
試しに4x4のユニタリ行列の位相推定ということで、$T$ゲートと$S$ゲートのテンソル積である以下のユニタリ行列について位相推定をしてみましょう。
\left[\begin{matrix}1 & 0 & 0 & 0\\0 & e^{\frac{i \pi}{4}} & 0 & 0\\0 & 0 & i & 0\\0 & 0 & 0 & i e^{\frac{i \pi}{4}}\end{matrix}\right]
今回はちゃんと位相推定ができていることを確認するので、固有ベクトルと固有値は既知ですが、それぞれの固有ベクトルの固有値、10進数表記の位相、2進数表記の位相をまとめると以下の通りです。
| 固有ベクトル | 固有値 | 10進数表記の位相 | 2進数表記の位相(2$\pi$は10進数) |
|---|---|---|---|
| $\ket{00}$ | $1$ | $0$ | $0.000\times2\pi$ |
| $\ket{01}$ | $e^{i{\pi/4}}$ | $\pi/4$ | $0.001\times2\pi$ |
| $\ket{10}$ | $e^{i{\pi/2}}$ | $\pi/2$ | $0.010\times2\pi$ |
| $\ket{11}$ | $e^{i{3\pi/4}}$ | $3\pi/4$ | $0.011\times2\pi$ |
つまり、例えば $\ket{01}$ を入力したら測定ビット側では $\ket{001}$ が測定されることが期待されます。
また、誤差なく位相推定をするには、2進数表記の位相の小数点以下の桁数から測定ビットが3個必要であることもわかります。
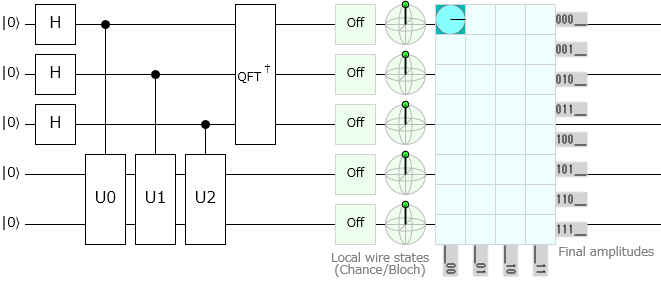
この回路をQuirkで表現してみましょう。すっきりと教科書どおりに書くとこのような感じの回路になります。
Quirkで表示する
ちなみにユニタリゲートの中身も愚直に表現して、かつ、$QFT^\dagger$の中身も表現してしまうとこのような感じの量子回路になります。
測定用ビットが3量子ビットだけにもかかわらず、ちょっと鬱陶しくなってしまいましたね。
Quirkで表示する
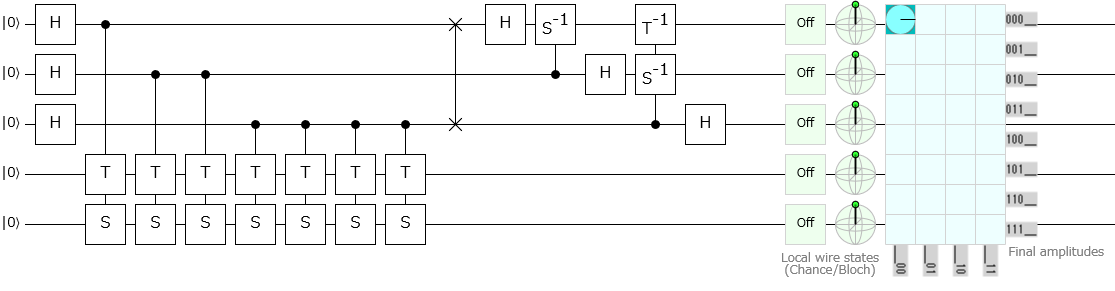
ではQuirkで作った回路に入力していきましょう。
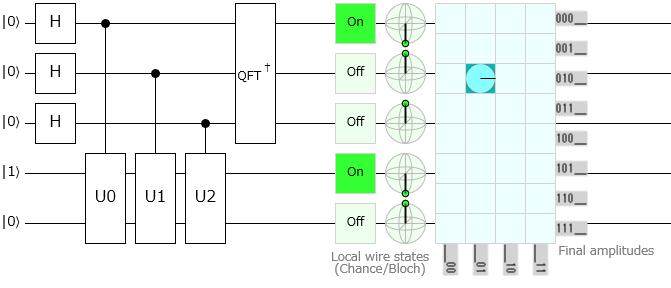
|00〉を入力する
測定ビットで $\ket{000}$ が観測されていますので、位相は $0$ と推定されたことになります。
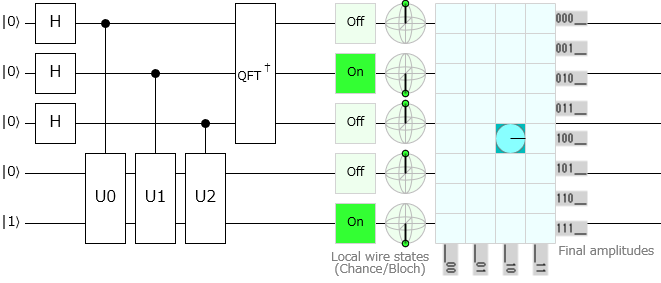
|01〉を入力する
測定ビットで $\ket{001}$ が観測されていますので、位相は $\pi/4$ と推定されたことになります。
|10〉を入力する
測定ビットで $\ket{010}$ が観測されていますので、位相は $\pi/2$ と推定されたことになります。
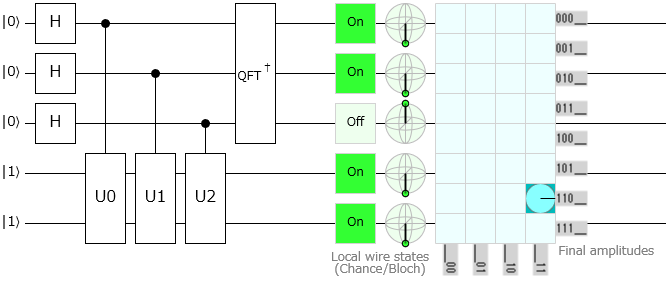
|11〉を入力する
測定ビットで $\ket{011}$ が観測されていますので、位相は $3\pi/4$ と推定されたことになります。
位相をバイナリで表現するのが難しいユニタリ行列に対してQPEを実行してみる
先程「位相を誤差なく表現できるビット数の分の測定ビットを用意しさえすれば、精度良くユニタリ行列の固有値を求めることができる」ということを言いました。
それでは位相をバイナリで誤差なく表現できないようなユニタリ行列に$QPE$を実行するとどうなるのでしょうか。
ここでは固有値の位相として$1/3\times2\pi$つまり$0.3333...\times2\pi$を持つ2x2のユニタリ行列 $U$ を考えます。
\left[\begin{matrix}1 & 0\\0 & e^{\frac{ i 2\pi}{3}}\end{matrix}\right]
このようなユニタリ行列の位相を精度良く推定することを考えてみましょう。
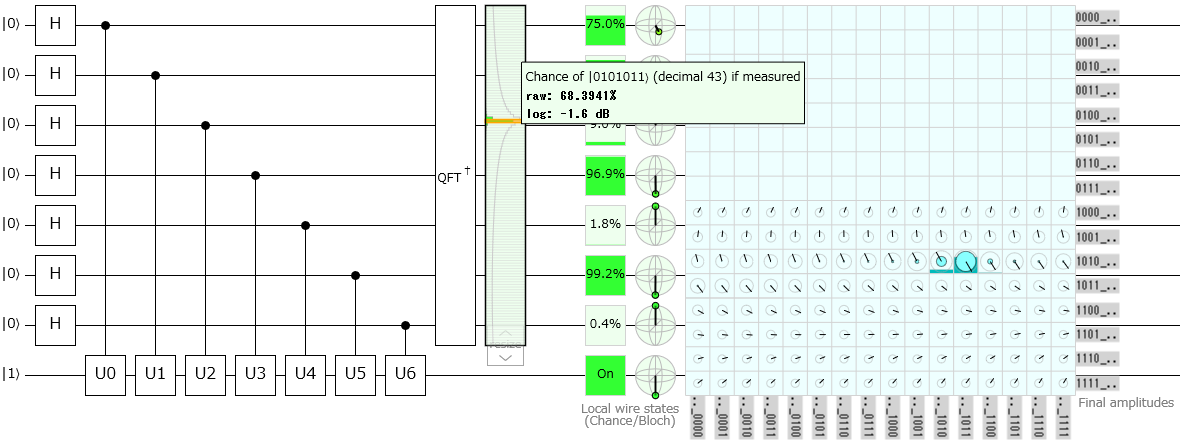
測定ビットを3つにして試してみる
$\ket{011}$の辺りが一番測定されますが、2進数で$0.011$は10進数で$0.375$なので$0.3333...$から比較すると正確と言えるか少しあやしいです。
ただ、この結果からして$0.25$と$0.375$の間で、かつ、$0.375$寄りのところに解がありそうなことはわかりますね。
もう少し精度を高めるために測定用の量子ビットを増やしてみましょう。
測定ビットを7つにする
$\ket{0101011}$が最も多く測定されています。
割り切れない数字なので当然ドンピシャの値は出せませんが、10進数に直すと$0.3359375$なので$0.3333...$にだいぶ近づいたことがわかります。
このように測定ビットを増やすことで位相推定の精度を高めることができることがお分かりいただけたかと思います。
最後に
$QFT$や$QPE$そのものについては偉大なる先人が詳しく分かりやすく解説しているので、そこはそちらを紹介しつつ(かつ、そちらにお任せしつつ)、視覚的に確認して直感的に理解してみようというのがこの記事の目的でした。
この2つの量子アルゴリズムは数々の応用的な量子アルゴリズムの基礎にもなっているアルゴリズムであり、量子コンピュータを扱う上で非常に重要な存在なので、その理解の助けになればと思います![]()
-
前日のAdventCalendarの記事をご参照ください https://qiita.com/shnchr/items/ae194ba81cd07f2277f6 ↩ ↩2