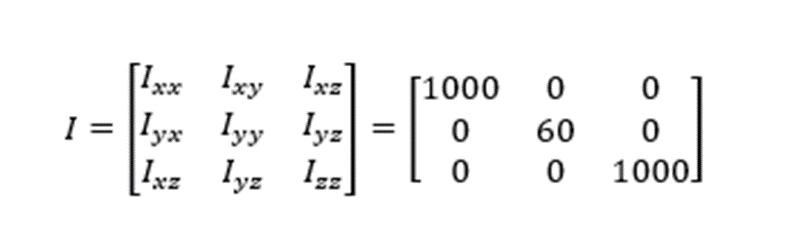こんにちは。九大院生ITストラテジストの岩附陽太です。
今回はクウォータニオンによる制御とオイラー角による制御の違いについて解説します。
目的
この記事では以下のような内容を確認できます。
・オイラー角とクォータニオンの両方で安定的な制御系の設計が可能であることこと(単なるPIDではありません。)
・オイラー角とクォータニオンの差異に起因する特異点周りの挙動の差異
・以下の論文の内容の制御を実際に実装しています。
クォータニオンを用いた小型電動ヘリコプタの姿勢制御
コードは一番最後にまとめてあります。
この記事は、九州大学の大学院の機器学特論という講義の課題で、実際に岩附が作った答案のマイナーチェンジになります。なお、数式はQiita用に書き直す体力がなかったので、レポートを画像化して対応している部分が多々あります。
制御とは
制御にはいろいろな意味合いがありますが、今回の制御は、ある目標に沿うように状態を変化させることです。例えば、航空機の制御、人工衛星の制御をはじめ広く機械で用いられます。航法誘導制御(GNC:guidance-navigation-control)がワンセットで、航法でセンサから現在の状態を推定し、誘導で目標を決め、制御で目標に沿うように変化させるという流れで用いられます。
オイラー角とは
オイラー角とは3次元の物体の回転を表すために用いられる回転角の組のことです。このブログの説明がわかりやすいです。「3次元空間における剛体または参照座標系の回転姿勢を表す方法の一つです。独立な3つの角度の組で回転姿勢を表し、便利で分かりやすいので、力学やコンピュータグラフィックスでもよく使われています。」という説明があります。ある軸周りに3回の回転を繰り返すことで、任意の姿勢への回転をすることができます。そこで飛行機の場合はわかりやすく、方位角、ピッチ角、バンク角、という、機体姿勢からわかりやすい角が使われます。オイラー角のデメリットとしては、特異姿勢の際にジンバルロックという自由度欠落によって姿勢が推定できなくなる問題があります。
クォータニオンとは
クォータニオンとは複素数を拡張したような概念で、四元数と呼ばれます。複素数では虚数がiのみですが、クォータニオンではi,j,kの3つの文字を導入して様々な計算を行います。ドローン工学入門・野波健蔵先生著にはクォータニオンについて以下のようなわかりやすい説明があります。
「クォータニオン(4元数,quaternion)は複素数を拡張した数体系で,1843年にウイリアムローワン・ハミルトン(William Rowan Hamilton)によって発見された.クォータニオンは20世紀の後半になって,3次元の自由な回転を記述しやすいことが明らかとなり,様々な分野で多用されることとなった.クォータニオンによる3次元の回転運動や姿勢表現は,3行3列の行列による表現と食らえて記憶容量が小さく演算のスピードが速い.加えて,オイラー角と違って特異点が存在しない.この特徴は3次元空間を自在に飛行するドローンや航空機の姿勢制御,ロケットや人工衛星の姿勢制御などへの利用にきわめて適している.さらにゲームやアニメーションで多用されるコンピュータグラフィックス,ロボット工学など,ほかにも多くの応用がある.」
シミュレーションの条件
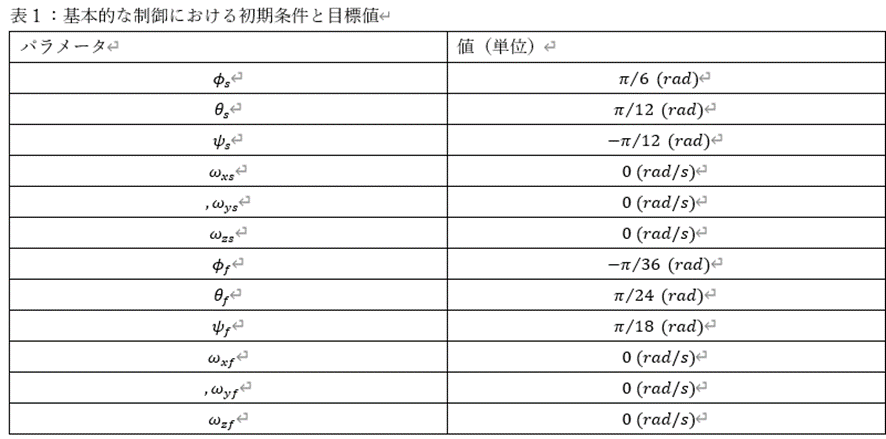
ここではクォータニオンを用いて、オイラーの固有軸によって初期姿勢から目標姿勢まで回転させる制御系を設計し、その挙動を求めるシミュレーションを作ります。そこで、表1の条件でクォータニオンのシミュレーション、オイラー角のシミュレーション両方が上手く機能していることを確かめ、表2でオイラー角の特異点周りの挙動を比較します。
慣性モーメントは以下のように置きました。
これは人力飛行機に近い慣性モーメントになっていますクォータニオンを使った航空機のフィードバック制御.基本的な制御ができていることを確認するための初期条件としてオイラー角と,機体軸周りの回転角速度
を表1の添え字sのように設定します.さらに制御の目標値として,オイラー角と,機体軸周りの回転角速度を表1の添え字fのように設定します.なおオイラー角のパラメータ設定の理由は特になく,ある程度原点(0に近い)値を選びました.
次に,オイラー角とクォータニオンの制御の比較ができていることを確認するための初期条件としてオイラー角と,機体軸周りの回転角速度を表2の添え字sのように設定します.さらに制御の目標値として,オイラー角と,機体軸周りの回転角速度を表2の添え字sのように設定します.オイラー角を用いたアルゴリズムではジンバルロックというθ=π/2の付近で特異点の影響により角度が正確に出せなくなる特徴があるので,その特徴がでやすい目標値を設定しました.
シミュレーションは0.1秒きざみで0秒から100秒までおこないました.
運動方程式の導出
[3] [宇宙航空研究開発機構特別資料 人工衛星の力学と制御 宇宙機ダイナミクス・姿勢制御技術ユニット] (https://jaxa.repo.nii.ac.jp/index.php?active_action=repository_view_main_item_detail&page_id=13&block_id=21&item_id=6101&item_no=1)
[4]ローター傾斜構造,ローター回転方向の非対称構造を有するマルチコプターの特性解析
岩附陽太 2021年度九州大学卒業論文
[5]クォータニオンを用いた小型電動ヘリコプタの姿勢制御 鈴木悟 中澤大輔 廣谷和之 野波健蔵 田原誠先生ら
クォータニオンを用いたアルゴリズムの数式的説明
ここでクォータニオンの導入を行います.クォータニオンの記述の仕方は,教科書によって異なりますが,今回は飛行力学(増補版) 嶋田有三 佐々木修一先生ら 森北出版に合わせて定義を行います.
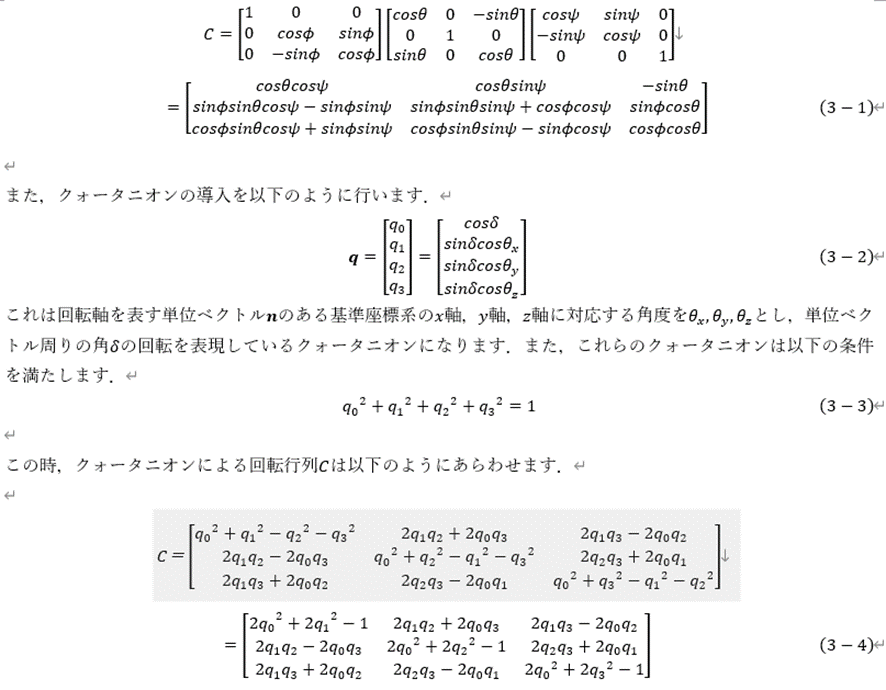
まずオイラー角から回転行列の変形について,オイラー角のロール角ピッチ角ヨー角をφ,
θ,Ψと対応させれば回転行列Cは以下のように定義できます.
よって回転行列からクォータニオンを表す式は以下のようになります.
[7]機器学特論講義資料 九州大学
結果
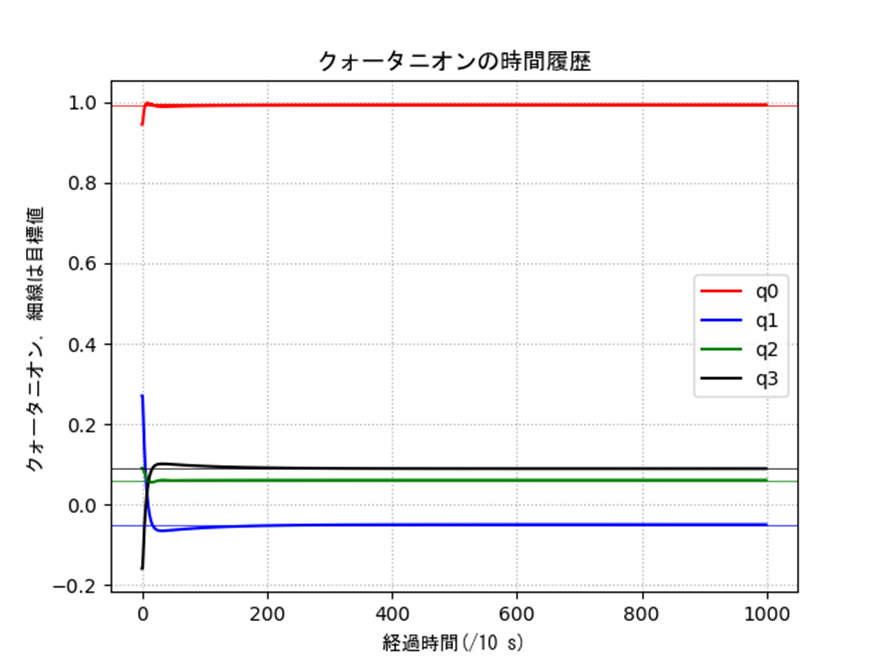
表1の条件に対する結果を示します。クォータニオンを用いた制御が上手くいっていることがわかります。またハイパーパラメータのK1、K2はそれぞれ30,10としました。これは条件を変えた試行錯誤の結果で、レポートには記載しましたが記事では過程が長くなるので省略します。コードを最後に乗せるので、気になる人はいじって挙動を観察してみてください。
オイラー角による制御のアルゴリズム
結果
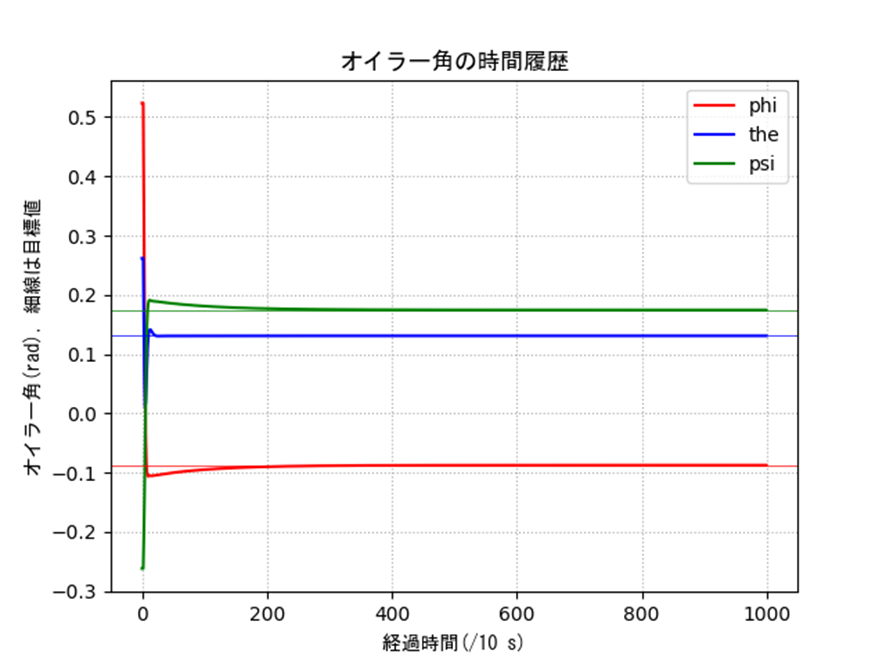
表1の結果に対するオイラー角による制御の結果を示します。問題なく制御できていることがわかります。
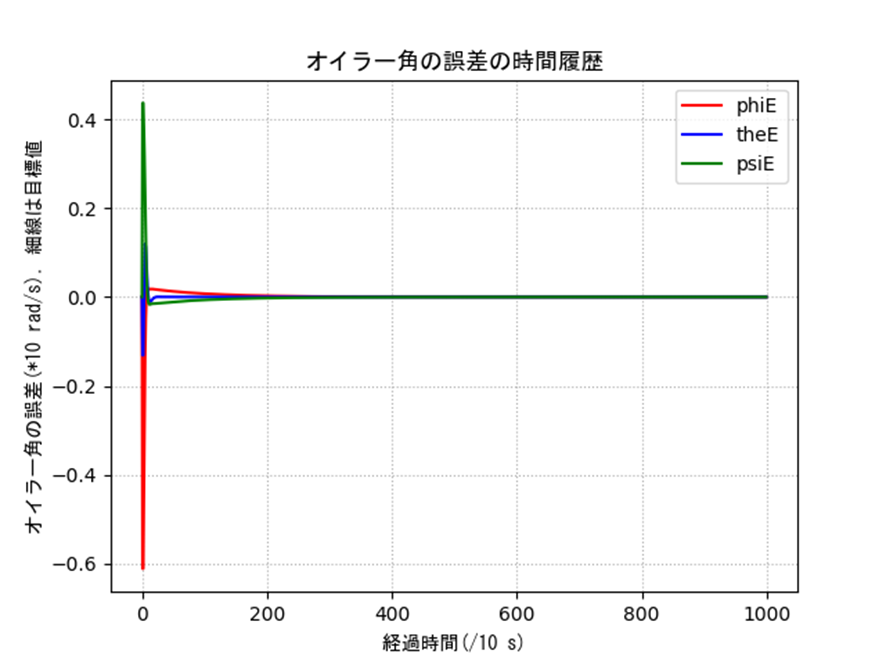
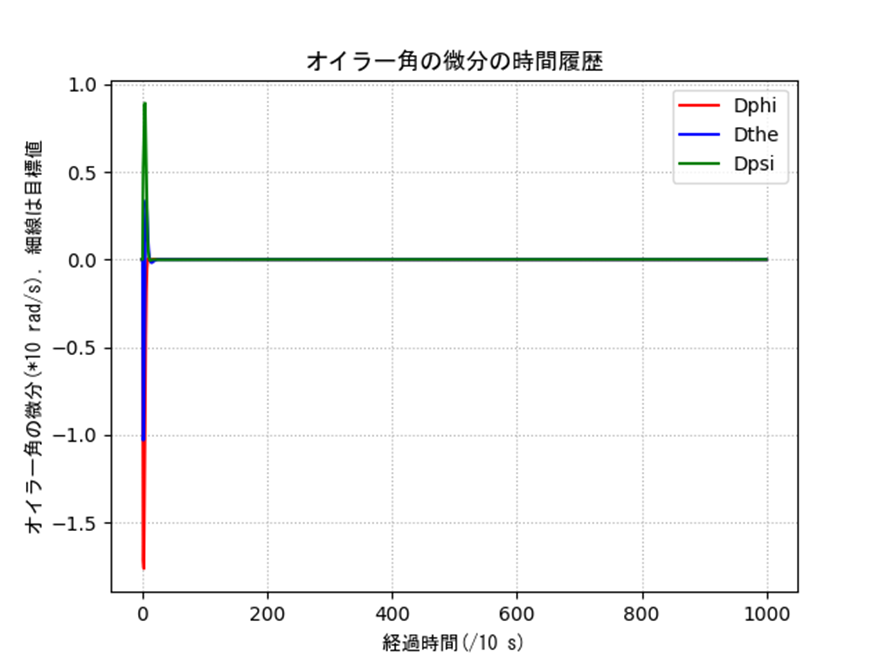
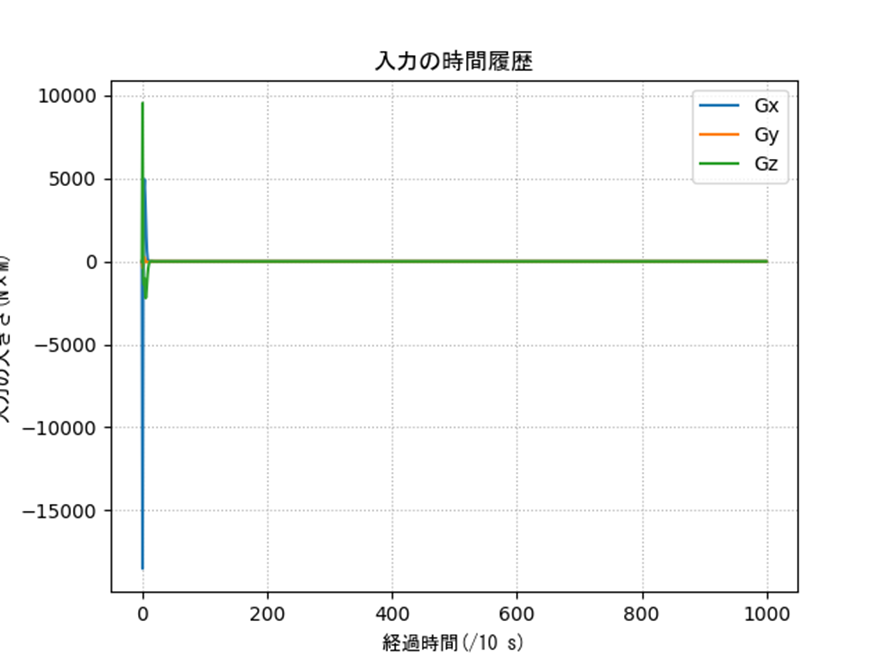
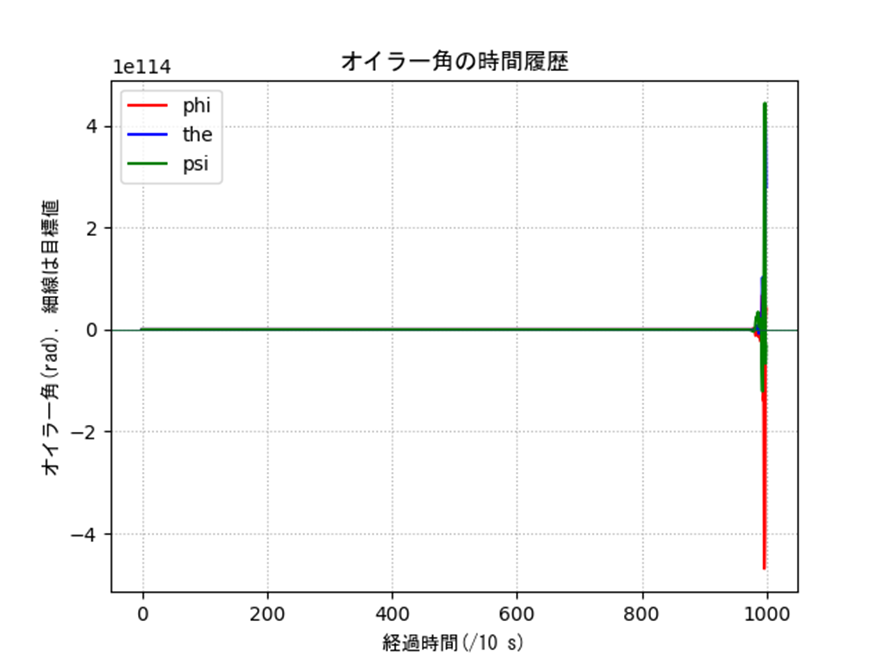
オイラー角によるジンバルロックの観察
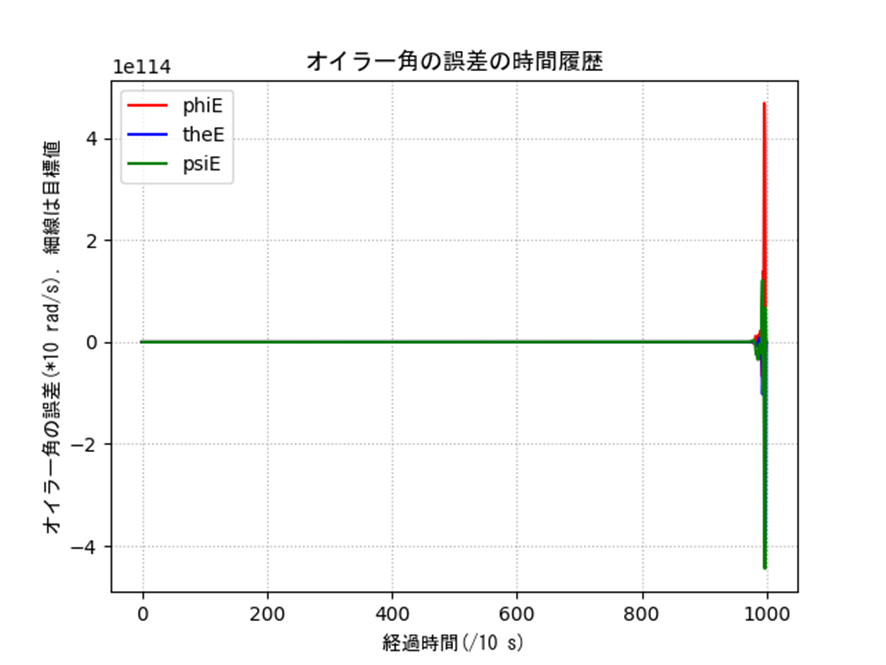
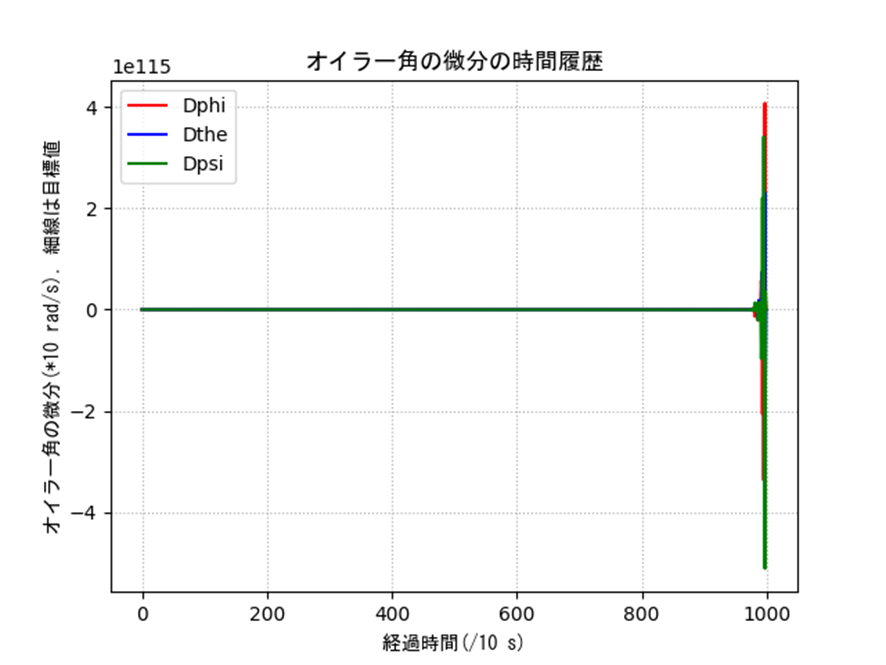
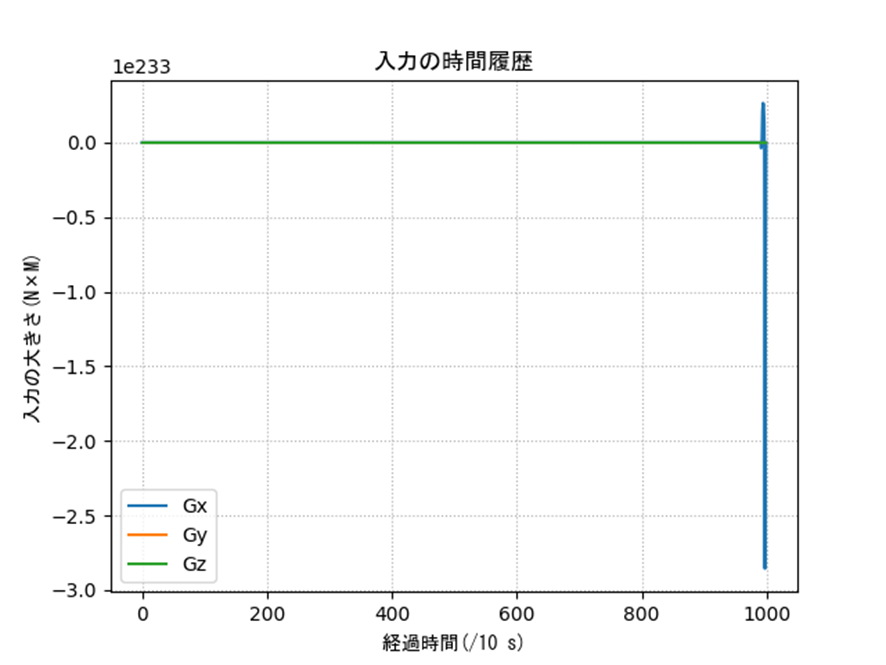
表2のオイラー角の特異点周りを含む条件におけるシミュレーション結果を示します。姿勢、入力ともに発散しているのがわかり、うまく制御できていないことがわかります。
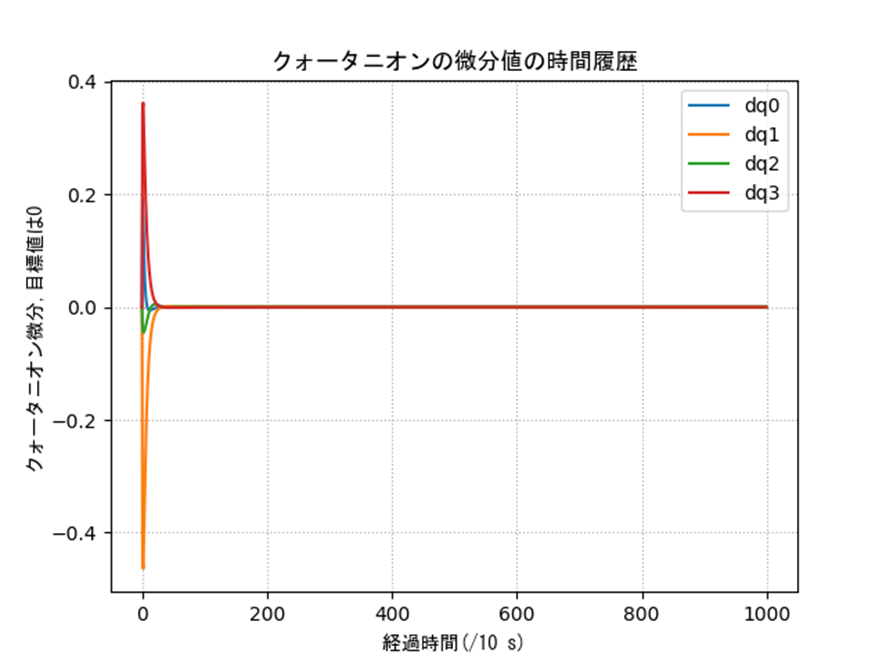
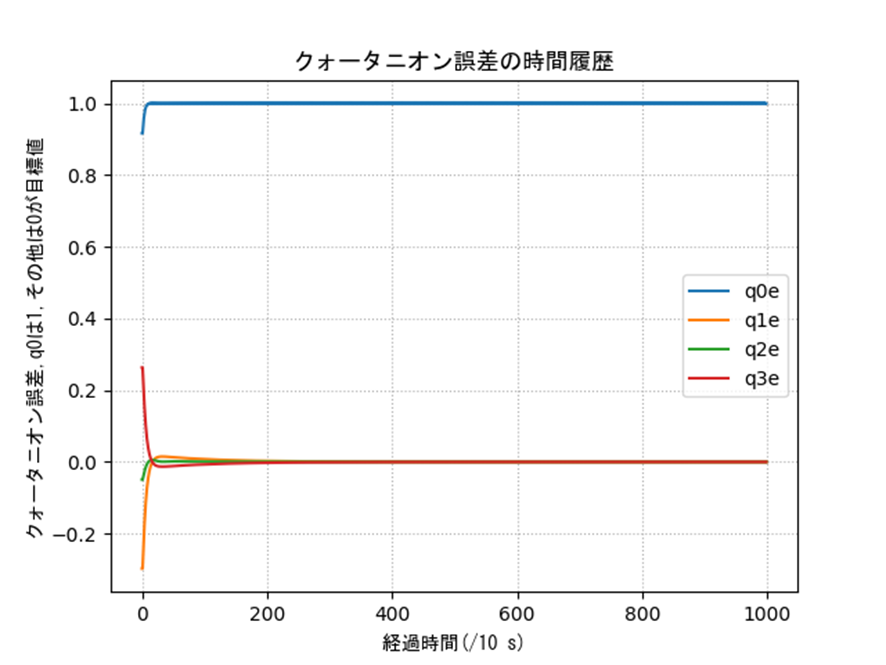
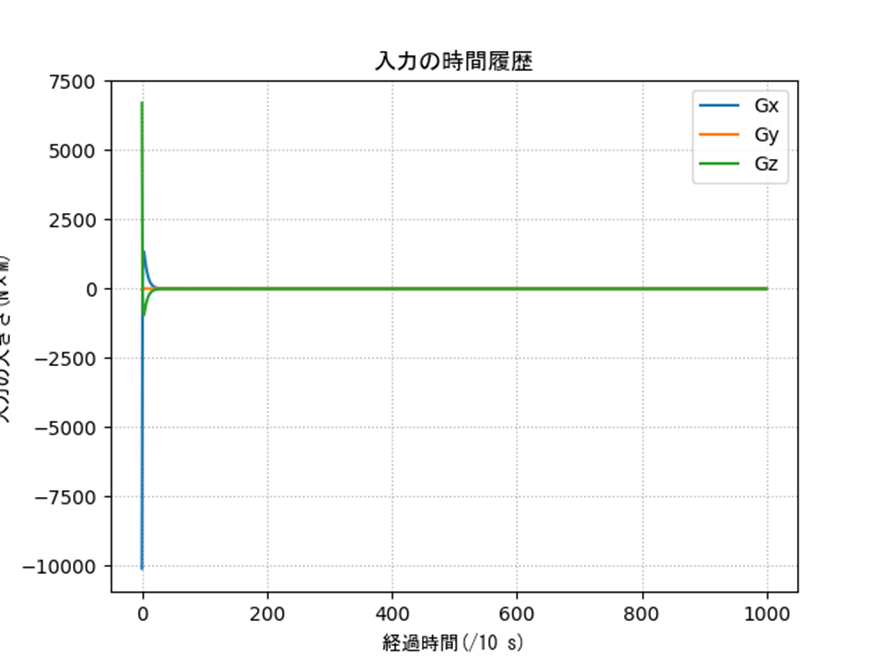
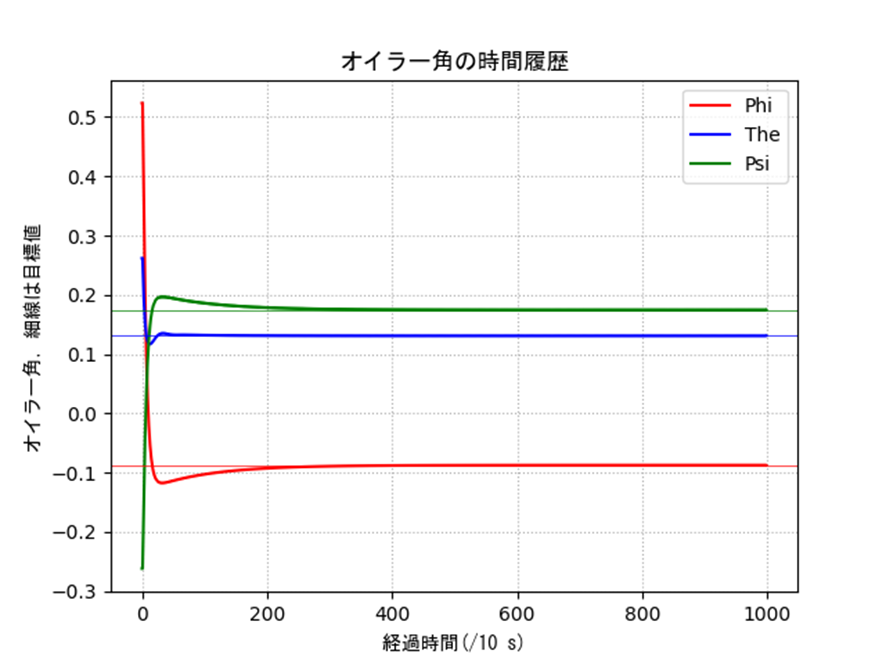
クォータニオンによる制御との比較
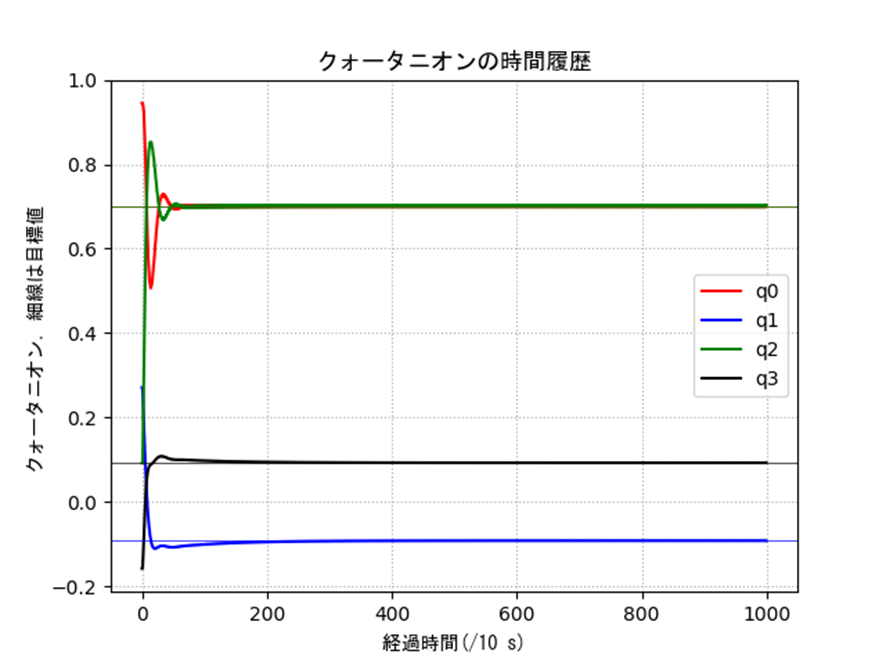
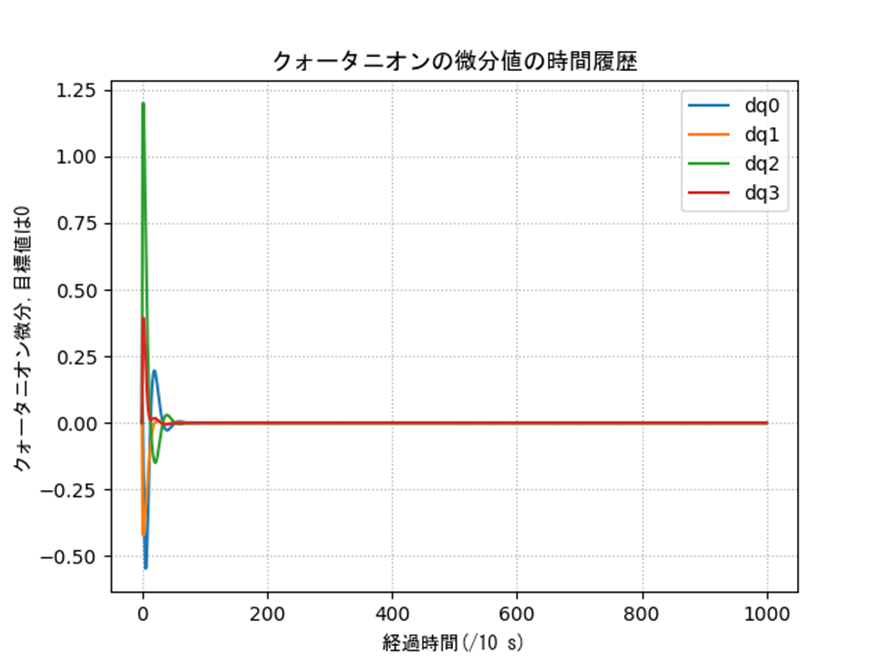
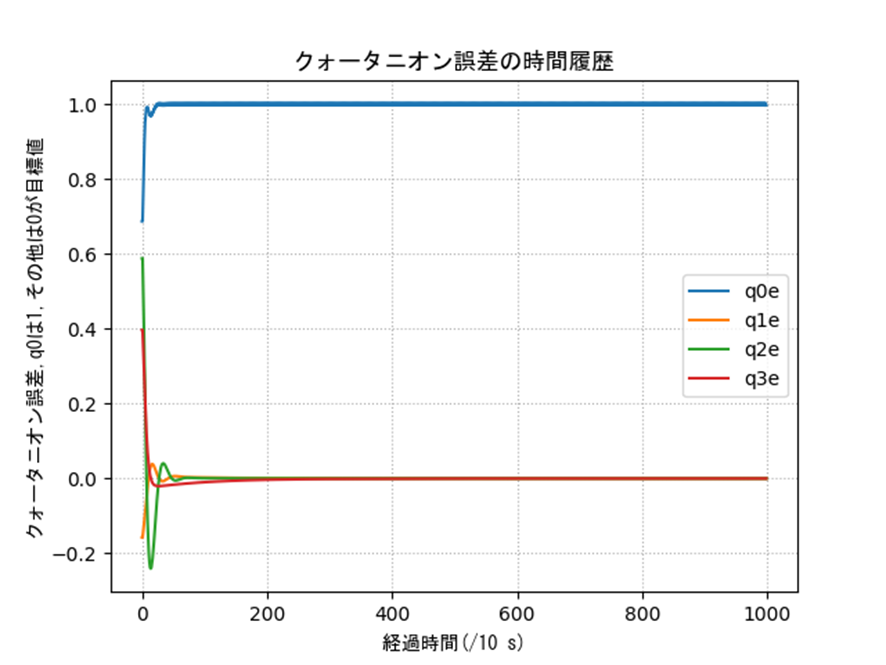
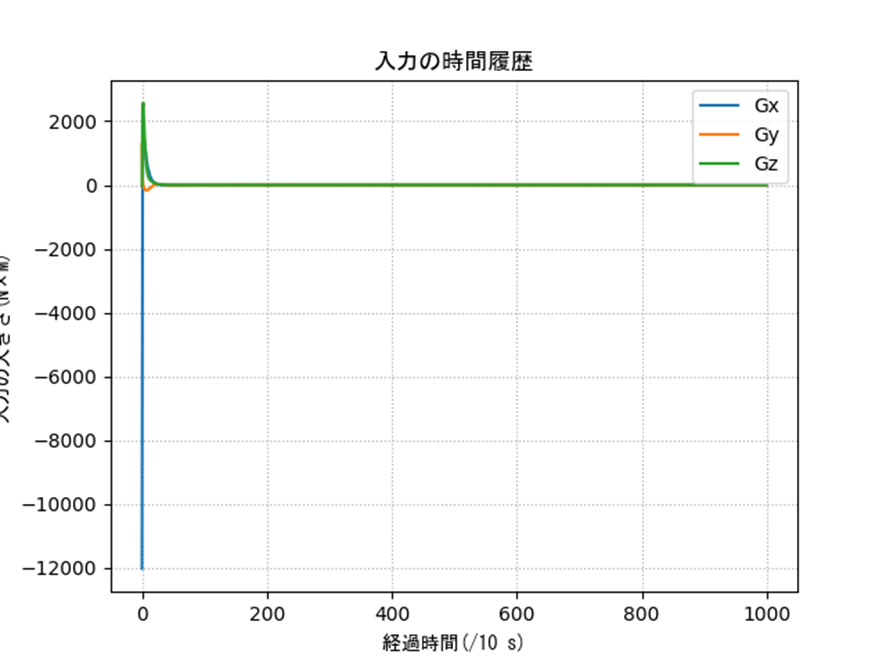
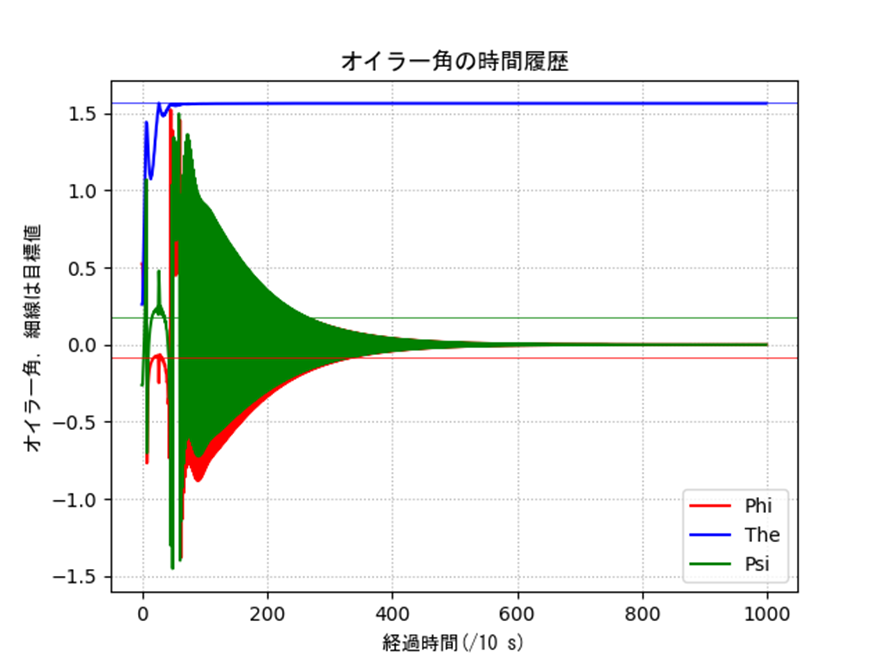
表2の条件に対するクォータニオンの結果を示します。姿勢や誤差などを見るとうまく制御できていることがわかります。一部のオイラー角に変換した際の入力は発散的に見えますが、これは以下のような理由です。特異姿勢周りなので、クォータニオン側では正しく計算できていても、人間に理解しやすいようにオイラー角に変換すると正しく表現できないということですね。実際は制御入力も発散していないクォータニオンを使って行うので、入力がバグることはありません。
結論
ジンバルロックが絡む3次元回転を扱うときは、オイラー角ではうまく制御できていません。ジンバルロックが絡む3次元回転を扱うとき、つまり機体が真上を向く可能性がある、たとえば人工衛星やロケットなどの制御や、故障時にロバストな制御系を作るときには、オイラー角ではなくクォータニオンを使うほうがベターであることが、シミュレーションからわかります。またオイラー角を用いた制御でP制御を行っている例は結構ネット上で見るのですが、リアプノフ関数で安定化させているものはあまり見ないので、誰かの参考になれば幸いです。
コード
クォータニオンを用いたプログラムの手順はこれです。
import numpy as np
import matplotlib.pyplot as plt
import math
import time
#時間作成
start=time.time()
#グラフを整える関数
def plot_set(fig_ax,args):
fig_ax.grid(ls=':') #グラフの補助線を点線で設定
fig_ax.legend(loc=args) #凡例の位置を3つ目の引数で設定
#オイラー角から回転行列
def EulerAngleToC(phi,the,psi):
C11=math.cos(the)*math.cos(psi)
C12=math.cos(the)*math.sin(psi)
C13=-math.sin(the)
C21=math.sin(phi)*math.sin(the)*math.cos(psi)-math.cos(phi)*math.sin(psi)
C22=math.sin(phi)*math.sin(the)*math.sin(psi)+math.cos(phi)*math.cos(psi)
C23=math.sin(phi)*math.cos(the)
C31=math.cos(phi)*math.sin(the)*math.cos(psi)+math.sin(phi)*math.sin(psi)
C32=math.cos(phi)*math.sin(the)*math.sin(psi)-math.sin(phi)*math.cos(psi)
C33=math.cos(phi)*math.cos(the)
C_Matrix=[[C11,C12,C13],[C21,C22,C23],[C31,C32,C33]]
return C_Matrix
#回転行列からクォータニオン
def CToQuaternion(C):
q0=1/2*((1+C[0][0]+C[1][1]+C[2][2])**(1/2))
q1=1/(4*q0)*(C[1][2]-C[2][1])
q2=1/(4*q0)*(C[2][0]-C[0][2])
q3=1/(4*q0)*(C[0][1]-C[1][0])
q=[q0,q1,q2,q3]
return q
#クオータニオンノルム
def NormQuaternion(q1):
q1x=q1[0]
q1y=q1[1]
q1z=q1[2]
q1w=q1[3]
Normq=math.sqrt(q1x*q1x+q1y*q1y+q1z*q1z+q1w*q1w)
return Normq
#クオータニオン微分
def QuaternionDelta(omega,q1):
ox=omega[0]
oy=omega[1]
oz=omega[2]
q10=q1[0]
q11=q1[1]
q12=q1[2]
q13=q1[3]
q20=(-ox*q11-oy*q12-oz*q13)/2
q21=(ox*q10+oz*q12-oy*q13)/2
q22=(oy*q10-oz*q11+ox*q13)/2
q23=(oz*q10+oy*q11-ox*q12)/2
q2=[q20,q21,q22,q23]
return q2
#共役クオータニオン
def ConjugateQuaternion(q1):
q1x=q1[0]
q1y=q1[1]
q1z=q1[2]
q1w=q1[3]
q2x=q1x
q2y=-q1y
q2z=-q1z
q2w=-q1w
q2=[q2x,q2y,q2z,q2w]
return q2
#q1が回転クオータニオン、q2が回転対象のクオータニオンになる。
def QuaternionProduct(q1,q2):
q1x=q1[0]
q1y=q1[1]
q1z=q1[2]
q1w=q1[3]
q2x=q2[0]
q2y=q2[1]
q2z=q2[2]
q2w=q2[3]
q3x=q1x*q2x - q1y*q2y - q1z*q2z - q1w*q2w
q3y=q1x*q2y + q1y*q2x + q1z*q2w - q1w*q2z
q3z=q1x*q2z - q1y*q2w + q1z*q2x + q1w*q2y
q3w=q1x*q2w + q1y*q2z - q1z*q2y + q1w*q2x
q3=[q3x,q3y,q3z,q3w]
return q3
#クォータニオンから回転行列
#確認済み
def QuaternionToC(q):
q0=q[0]
q1=q[1]
q2=q[2]
q3=q[3]
C11=2*q0*q0-1+2*q1*q1
C12=2*q1*q2+2*q0*q3
C13=2*q1*q3-2*q0*q2
C21=2*q1*q2-2*q0*q3
C22=2*q0*q0-1+2*q2*q2
C23=2*q2*q3+2*q0*q1
C31=2*q1*q3+2*q0*q2
C32=2*q2*q3-2*q0*q1
C33=2*q0*q0-1+2*q3*q3
C_Matrix=[[C11,C12,C13],[C21,C22,C23],[C31,C32,C33]]
return C_Matrix
#回転行列からオイラー角
#確認済み
def CToEulerAngle(C):
if float(C[2][2])==0:
C[2][2]=0.0000001
if float(C[0][0])==0:
C[0][0]=0.0000001
phi=math.atan(float(C[1][2])/float(C[2][2]))
the=math.atan(-float(C[0][2])/math.sqrt(float(C[1][2])*float(C[1][2])+float(C[2][2])*float(C[2][2])))
psi=math.atan(float(C[0][1])/float(C[0][0]))
return phi,the,psi
#誤差クォータニオンの計算
def ErrorQuaternion(qf,q):
qc=ConjugateQuaternion(q)
qe=QuaternionProduct(qf,qc)
return qe
#行列の掛け算4×4*1×4
def ProductMatrixSmall(Ms44,ms14):
M11=Ms44[0][0]
M12=Ms44[0][1]
M13=Ms44[0][2]
M14=Ms44[0][3]
M21=Ms44[1][0]
M22=Ms44[1][1]
M23=Ms44[1][2]
M24=Ms44[1][3]
M31=Ms44[2][0]
M32=Ms44[2][1]
M33=Ms44[2][2]
M34=Ms44[2][3]
M41=Ms44[3][0]
M42=Ms44[3][1]
M43=Ms44[3][2]
M44=Ms44[3][3]
m11=ms14[0]
m12=ms14[1]
m13=ms14[2]
m14=ms14[3]
Nm11=M11*m11+M12*m12+M13*m13+M14*m14
Nm12=M21*m11+M22*m12+M23*m13+M24*m14
Nm13=M31*m11+M32*m12+M33*m13+M34*m14
Nm14=M41*m11+M42*m12+M43*m13+M44*m14
NM=[Nm11,Nm12,Nm13,Nm14]
return NM
#行列の掛け算4×4*4×4
def ProductMatrix(Ms44,ms44):
M11=Ms44[0][0]
M12=Ms44[0][1]
M13=Ms44[0][2]
M14=Ms44[0][3]
M21=Ms44[1][0]
M22=Ms44[1][1]
M23=Ms44[1][2]
M24=Ms44[1][3]
M31=Ms44[2][0]
M32=Ms44[2][1]
M33=Ms44[2][2]
M34=Ms44[2][3]
M41=Ms44[3][0]
M42=Ms44[3][1]
M43=Ms44[3][2]
M44=Ms44[3][3]
m11=ms44[0][0]
m12=ms44[0][1]
m13=ms44[0][2]
m14=ms44[0][3]
m21=ms44[1][0]
m22=ms44[1][1]
m23=ms44[1][2]
m24=ms44[1][3]
m31=ms44[2][0]
m32=ms44[2][1]
m33=ms44[2][2]
m34=ms44[2][3]
m41=ms44[3][0]
m42=ms44[3][1]
m43=ms44[3][2]
m44=ms44[3][3]
Nm11=M11*m11+M12*m21+M13*m31+M14*m41
Nm12=M11*m12+M12*m22+M13*m32+M14*m42
Nm13=M11*m13+M12*m23+M13*m33+M14*m43
Nm14=M11*m14+M12*m24+M13*m34+M14*m44
Nm21=M21*m11+M22*m21+M23*m31+M24*m41
Nm22=M21*m12+M22*m22+M23*m32+M24*m42
Nm23=M21*m13+M22*m23+M23*m33+M24*m43
Nm24=M21*m14+M22*m24+M23*m34+M24*m44
Nm31=M31*m11+M32*m21+M33*m31+M34*m41
Nm32=M31*m12+M32*m22+M33*m32+M34*m42
Nm33=M31*m13+M32*m23+M33*m33+M34*m43
Nm34=M31*m14+M32*m24+M33*m34+M34*m44
Nm41=M41*m11+M42*m21+M43*m31+M44*m41
Nm42=M41*m12+M42*m22+M43*m32+M44*m42
Nm43=M41*m13+M42*m23+M43*m33+M44*m43
Nm44=M41*m14+M42*m24+M43*m34+M44*m44
NM=[[Nm11,Nm12,Nm13,Nm14],[Nm21,Nm22,Nm23,Nm24],[Nm31,Nm32,Nm33,Nm34],[Nm41,Nm42,Nm43,Nm44]]
return NM
#クォータニオンからクォータニオン積のD(q)行列を作る関数
def MakeDq(q):
q0=q[0]
q1=q[1]
q2=q[2]
q3=q[3]
D11=q0
D12=-q1
D13=-q2
D14=-q3
D21=q1
D22=q0
D23=-q3
D24=q2
D31=q2
D32=q3
D33=q0
D34=-q1
D41=q3
D42=-q2
D43=q1
D44=q0
Dq=[[D11,D12,D13,D14],[D21,D22,D23,D24],[D31,D32,D33,D34],[D41,D42,D43,D44]]
return Dq
#---ここからmain---
pi=math.pi
#---ハイパーパラメータの設定---
DeltaT=0.1
FinalT=100
dt=0.1
K1=30
K2=10
PhiS=pi/6
TheS=pi/12
PsiS=-pi/12
#もともとの値
PhiF=-pi/36
TheF=pi/24
#TheF=pi/2
PsiF=pi/18
Ixx=1000
Iyy=60
Izz=1000
#初期姿勢の回転行列
Cs=EulerAngleToC(PhiS,TheS,PsiS)
#初期姿勢のクォータニオン
Qs=CToQuaternion(Cs)
print(Qs,NormQuaternion(Qs),'start')
#最終姿勢の回転行列
Cf=EulerAngleToC(PhiF,TheF,PsiF)
#最終姿勢のクォータニオン
Qf=CToQuaternion(Cf)
print(Qf,NormQuaternion(Qf),'final')
SimT=np.arange(0,FinalT,DeltaT)
LenSimT=len(SimT)
#オイラー角
Phi=[PhiS for i in range(0,LenSimT-1)]
The=[TheS for i in range(0,LenSimT-1)]
Psi=[PsiS for i in range(0,LenSimT-1)]
#クォータニオン
Q0=[Qs[0] for i in range(0,LenSimT)]
Q1=[Qs[1] for i in range(0,LenSimT)]
Q2=[Qs[2] for i in range(0,LenSimT)]
Q3=[Qs[3] for i in range(0,LenSimT)]
#回転行列
C11=[Cs[0][0] for i in range(0,LenSimT)]
C12=[Cs[0][1] for i in range(0,LenSimT)]
C13=[Cs[0][2] for i in range(0,LenSimT)]
C21=[Cs[1][0] for i in range(0,LenSimT)]
C22=[Cs[1][1] for i in range(0,LenSimT)]
C23=[Cs[1][2] for i in range(0,LenSimT)]
C31=[Cs[2][0] for i in range(0,LenSimT)]
C32=[Cs[2][1] for i in range(0,LenSimT)]
C33=[Cs[2][2] for i in range(0,LenSimT)]
#オイラー角の差分
PhiE=[0 for i in range(0,LenSimT)]
TheE=[0 for i in range(0,LenSimT)]
PsiE=[0 for i in range(0,LenSimT)]
#クォータニオンエラー
Q0E=[0 for i in range(0,LenSimT-1)]
Q1E=[0 for i in range(0,LenSimT-1)]
Q2E=[0 for i in range(0,LenSimT-1)]
Q3E=[0 for i in range(0,LenSimT-1)]
#Omega 機体軸周りの回転角速度
Ox=[0 for i in range(0,LenSimT)]
Oy=[0 for i in range(0,LenSimT)]
Oz=[0 for i in range(0,LenSimT)]
#Delta_Omega 機体軸周りの回転加角速度
Dox=[0 for i in range(0,LenSimT)]
Doy=[0 for i in range(0,LenSimT)]
Doz=[0 for i in range(0,LenSimT)]
#クォータニオンの微分
Dq0=[0 for i in range(0,LenSimT)]
Dq1=[0 for i in range(0,LenSimT)]
Dq2=[0 for i in range(0,LenSimT)]
Dq3=[0 for i in range(0,LenSimT)]
#入力
Gx=[0 for i in range(0,LenSimT)]
Gy=[0 for i in range(0,LenSimT)]
Gz=[0 for i in range(0,LenSimT)]
#入力のための誤差角速度
Gox=[0 for i in range(0,LenSimT)]
Goy=[0 for i in range(0,LenSimT)]
Goz=[0 for i in range(0,LenSimT)]
#入力のための誤差加角速度
Gdox=[0 for i in range(0,LenSimT)]
Gdoy=[0 for i in range(0,LenSimT)]
Gdoz=[0 for i in range(0,LenSimT)]
GxTotal=0
GyTotal=0
GzTotal=0
MakeDq1=[[-1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]]
MakeDq2=[[1,0,0,0],[0,-1,0,0],[0,0,-1,0],[0,0,0,-1]]
for i in range(0,LenSimT-1):
qnow=[Q0[i],Q1[i],Q2[i],Q3[i]]
[Q0E[i],Q1E[i],Q2E[i],Q3E[i]]=ErrorQuaternion(Qf,qnow)
Onow=[Ox[i],Oy[i],Oz[i]]
[Dq0[i],Dq1[i],Dq2[i],Dq3[i]]=QuaternionDelta(Onow,qnow)
O0now=[0,Ox[i],Oy[i],Oz[i]]
Gtemp=ProductMatrix(MakeDq1,ProductMatrix(MakeDq(Qf),ProductMatrix(MakeDq2,MakeDq(qnow))))
Gox[i+1]=Gtemp[0][1]*(1-Q0E[i])+Gtemp[1][1]*Q1E[i]+Gtemp[2][1]*Q2E[i]+Gtemp[3][1]*Q3E[i]
Goy[i+1]=Gtemp[0][2]*(1-Q0E[i])+Gtemp[1][2]*Q1E[i]+Gtemp[2][2]*Q2E[i]+Gtemp[3][2]*Q3E[i]
Goz[i+1]=Gtemp[0][3]*(1-Q0E[i])+Gtemp[1][3]*Q1E[i]+Gtemp[2][3]*Q2E[i]+Gtemp[3][3]*Q3E[i]
Gdox[i+1]=Gox[i+1]-Gox[i]
Gdoy[i+1]=Goy[i+1]-Goy[i]
Gdoz[i+1]=Goz[i+1]-Goz[i]
Gx[i]=(Izz-Iyy)*Oy[i]*Oz[i]-Ixx*K1*Gdox[i+1]-Gox[i+1]-K2*(Ox[i]+K1*Gox[i+1])
Gy[i]=(Ixx-Izz)*Ox[i]*Oz[i]-Iyy*K1*Gdoy[i+1]-Goy[i+1]-K2*(Oy[i]+K1*Goy[i+1])
Gz[i]=(Iyy-Ixx)*Ox[i]*Oy[i]-Izz*K1*Gdoz[i+1]-Goz[i+1]-K2*(Oz[i]+K1*Goz[i+1])
GxTotal=GxTotal+Gx[i]
GyTotal=GyTotal+Gx[i]
GzTotal=GzTotal+Gx[i]
Dox[i]=(Gx[i]-(Izz-Iyy)*Oy[i]*Oz[i])/Ixx
Doy[i]=(Gy[i]-(Ixx-Izz)*Ox[i]*Oz[i])/Iyy
Doz[i]=(Gz[i]-(Iyy-Ixx)*Ox[i]*Oy[i])/Izz
Qtemp0=Q0[i]+DeltaT*Dq0[i]
Qtemp1=Q1[i]+DeltaT*Dq1[i]
Qtemp2=Q2[i]+DeltaT*Dq2[i]
Qtemp3=Q3[i]+DeltaT*Dq3[i]
Q0[i+1]=Qtemp0/(Qtemp0**2+Qtemp1**2+Qtemp2**2+Qtemp3**2)
Q1[i+1]=Qtemp1/(Qtemp0**2+Qtemp1**2+Qtemp2**2+Qtemp3**2)
Q2[i+1]=Qtemp2/(Qtemp0**2+Qtemp1**2+Qtemp2**2+Qtemp3**2)
Q3[i+1]=Qtemp3/(Qtemp0**2+Qtemp1**2+Qtemp2**2+Qtemp3**2)
Ox[i+1]=Ox[i]+DeltaT*Dox[i]
Oy[i+1]=Oy[i]+DeltaT*Doy[i]
Oz[i+1]=Oz[i]+DeltaT*Doz[i]
[[C11[i],C12[i],C13[i]],[C21[i],C22[i],C23[i]],[C31[i],C32[i],C33[i]]]=QuaternionToC(qnow)
CTemp=[[C11[i],C12[i],C13[i]],[C21[i],C22[i],C23[i]],[C31[i],C32[i],C33[i]]]
[Phi[i],The[i],Psi[i]]=CToEulerAngle(CTemp)
fig,ax=plt.subplots()
ax.plot(Q0,label='q0', color = 'r')
ax.plot(Q1,label='q1', color = 'b')
ax.plot(Q2,label='q2', color = 'g')
ax.plot(Q3,label='q3', color = 'k')
ax.axhline(Qf[0], color = 'r', linewidth = 0.5)
ax.axhline(Qf[1], color = 'b', linewidth = 0.5)
ax.axhline(Qf[2], color = 'g', linewidth = 0.5)
ax.axhline(Qf[3], color = 'k', linewidth = 0.5)
ax.set_title('クォータニオンの時間履歴',fontname='MS Gothic')
ax.set_xlabel('経過時間(/10 s)',fontname='MS Gothic')
ax.set_ylabel('クォータニオン,細線は目標値',fontname='MS Gothic')
plot_set(ax,'best')
fig,ax2=plt.subplots()
ax2.plot(Dq0,label='dq0')
ax2.plot(Dq1,label='dq1')
ax2.plot(Dq2,label='dq2')
ax2.plot(Dq3,label='dq3')
ax2.set_title('クォータニオンの微分値の時間履歴',fontname='MS Gothic')
ax2.set_xlabel('経過時間(/10 s)',fontname='MS Gothic')
ax2.set_ylabel('クォータニオン微分,目標値は0',fontname='MS Gothic')
plot_set(ax2,'best')
fig,ax3=plt.subplots()
ax3.plot(Q0E,label='q0e')
ax3.plot(Q1E,label='q1e')
ax3.plot(Q2E,label='q2e')
ax3.plot(Q3E,label='q3e')
ax3.set_title('クォータニオン誤差の時間履歴',fontname='MS Gothic')
ax3.set_xlabel('経過時間(/10 s)',fontname='MS Gothic')
ax3.set_ylabel('クォータニオン誤差,q0は1,その他は0が目標値',fontname='MS Gothic')
plot_set(ax3,'best')
fig,ax4=plt.subplots()
ax4.plot(Gx,label='Gx')
ax4.plot(Gy,label='Gy')
ax4.plot(Gz,label='Gz')
ax4.set_title('入力の時間履歴',fontname='MS Gothic')
ax4.set_xlabel('経過時間(/10 s)',fontname='MS Gothic')
ax4.set_ylabel('入力の大きさ(N×M)',fontname='MS Gothic')
plot_set(ax4,'best')
fig,ax5=plt.subplots()
ax5.plot(Phi,label='Phi',color = 'r')
ax5.plot(The,label='The', color = 'b')
ax5.plot(Psi,label='Psi', color = 'g')
ax5.axhline(PhiF, color = 'r', linewidth = 0.5)
ax5.axhline(TheF, color = 'b', linewidth = 0.5)
ax5.axhline(PsiF, color = 'g', linewidth = 0.5)
ax5.set_title('オイラー角の時間履歴',fontname='MS Gothic')
ax5.set_xlabel('経過時間(/10 s)',fontname='MS Gothic')
ax5.set_ylabel('オイラー角,細線は目標値',fontname='MS Gothic')
plot_set(ax5,'best')
plt.show()
print('GxTotal',GxTotal,'GyTotal',GyTotal,'GzTotal',GzTotal)
#計算時間の図示
print('computing time is ',time.time()-start)
print('finish')
オイラー角のコード
オイラー角を用いた手順はこれです。
import numpy as np
import matplotlib.pyplot as plt
import math
import time
import os
#時間作成
start=time.time()
#グラフを整える関数
def plot_set(fig_ax, args):
fig_ax.grid(ls=':') #グラフの補助線を点線で設定
fig_ax.legend(loc=args) #凡例の位置を3つ目の引数で設定
#オイラー角から回転行列
#確認済み
def EulerAngleToC(phi,the,psi):
C11=math.cos(the)*math.cos(psi)
C12=math.cos(the)*math.sin(psi)
C13=-math.sin(the)
C21=math.sin(phi)*math.sin(the)*math.cos(psi)-math.cos(phi)*math.sin(psi)
C22=math.sin(phi)*math.sin(the)*math.sin(psi)+math.cos(phi)*math.cos(psi)
C23=math.sin(phi)*math.cos(the)
C31=math.cos(phi)*math.sin(the)*math.cos(psi)+math.sin(phi)*math.sin(psi)
C32=math.cos(phi)*math.sin(the)*math.sin(psi)-math.sin(phi)*math.cos(psi)
C33=math.cos(phi)*math.cos(the)
C_Matrix=[[C11,C12,C13],[C21,C22,C23],[C31,C32,C33]]
return C_Matrix
#回転行列からオイラー角
#確認済み
def CToEulerAngle(C):
#print(C)
if float(C[2][2])==0:
C[2][2]=0.0001
if float(C[0][0])==0:
C[0][0]=0.0001
phi=math.atan(float(C[1][2])/float(C[2][2]))
the=math.atan(-float(C[0][2])/math.sqrt(float(C[1][2])*float(C[1][2])+float(C[2][2])*float(C[2][2])))
psi=math.atan(float(C[0][1])/float(C[0][0]))
return phi,the,psi
#---ここからmain---
pi=math.pi
#---ハイパーパラメータの設定---
DeltaT=0.1
FinalT=100
dt=0.1
alp=1
beta=5
K1=30
K2=10
K3=0.5
PhiS=pi/6
TheS=pi/12
PsiS=-pi/12
#PhiF=pi/3
#TheF=pi/9
#PsiF=pi/2
#もともとの値
PhiF=-pi/36
#TheF=pi/24
TheF=pi/2
PsiF=pi/18
Ixx=1000
Iyy=60
Izz=1000
#初期姿勢の回転行列
Cs=EulerAngleToC(PhiS,TheS,PsiS)
#最終姿勢の回転行列
Cf=EulerAngleToC(PhiF,TheF,PsiF)
SimT=np.arange(0,FinalT,DeltaT)
LenSimT=len(SimT)
#オイラー角
Phi=[PhiS for i in range(0,LenSimT)]
The=[TheS for i in range(0,LenSimT)]
Psi=[PsiS for i in range(0,LenSimT)]
#回転行列
C11=[Cs[0][0] for i in range(0,LenSimT)]
C12=[Cs[0][1] for i in range(0,LenSimT)]
C13=[Cs[0][2] for i in range(0,LenSimT)]
C21=[Cs[1][0] for i in range(0,LenSimT)]
C22=[Cs[1][1] for i in range(0,LenSimT)]
C23=[Cs[1][2] for i in range(0,LenSimT)]
C31=[Cs[2][0] for i in range(0,LenSimT)]
C32=[Cs[2][1] for i in range(0,LenSimT)]
C33=[Cs[2][2] for i in range(0,LenSimT)]
#オイラー角の微分
Dphi=[0 for i in range(0,LenSimT)]
Dthe=[0 for i in range(0,LenSimT)]
Dpsi=[0 for i in range(0,LenSimT)]
#オイラー角のエラー
PhiE=[0 for i in range(0,LenSimT)]
TheE=[0 for i in range(0,LenSimT)]
PsiE=[0 for i in range(0,LenSimT)]
#Omega 機体軸周りの回転角速度
Ox=[0 for i in range(0,LenSimT)]
Oy=[0 for i in range(0,LenSimT)]
Oz=[0 for i in range(0,LenSimT)]
#Delta_Omega 機体軸周りの回転加角速度
Dox=[0 for i in range(0,LenSimT)]
Doy=[0 for i in range(0,LenSimT)]
Doz=[0 for i in range(0,LenSimT)]
#入力
Gx=[0 for i in range(0,LenSimT)]
Gy=[0 for i in range(0,LenSimT)]
Gz=[0 for i in range(0,LenSimT)]
#入力のための誤差角速度
Gox=[0 for i in range(0,LenSimT)]
Goy=[0 for i in range(0,LenSimT)]
Goz=[0 for i in range(0,LenSimT)]
#入力のための誤差加角速度
Gdox=[0 for i in range(0,LenSimT)]
Gdoy=[0 for i in range(0,LenSimT)]
Gdoz=[0 for i in range(0,LenSimT)]
GxTotal=0
GyTotal=0
GzTotal=0
for i in range(1,LenSimT-1):
PhiE[i]=PhiF-Phi[i]
TheE[i]=TheF-The[i]
PsiE[i]=PsiF-Psi[i]
Dphi[i]=Ox[i]+(Oy[i]*math.sin(Phi[i])+Oz[i]*math.cos(Phi[i]))*math.tan(The[i])
Dthe[i]=(Oy[i]*math.cos(Phi[i])-Oz[i]*math.sin(Phi[i]))
Dpsi[i]=(Oy[i]*math.sin(Phi[i])+Oz[i]*math.cos(Phi[i]))/math.cos(The[i])
Gox[i]=K1*PhiE[i]
Goy[i]=K1*(math.sin(Phi[i])*math.cos(The[i])*PhiE[i] + math.cos(Phi[i])*TheE[i] + math.sin(Phi[i])/math.cos(The[i])*PsiE[i])
Goz[i]=K1*(math.cos(Phi[i])*math.tan(The[i])*PhiE[i] - math.sin(Phi[i])*TheE[i] + math.cos(Phi[i])/math.cos(The[i])*PsiE[i])
Gdox[i]=Gox[i]-Gox[i-1]
Gdoy[i]=Goy[i]-Goy[i-1]
Gdoz[i]=Goz[i]-Goz[i-1]
#K1=10,K2=5でうまくいく
Gx[i]=(Izz-Iyy)*Oy[i]*Oz[i] + (PhiE[i]-PsiE[i]*math.sin(The[i])) + Ixx*Gdox[i] - K2*(Ox[i]-Gox[i])
Gy[i]=(Ixx-Izz)*Ox[i]*Oz[i] + (TheE[i]*math.cos(Phi[i])+PsiE[i]*math.sin(The[i])*math.cos(The[i])) + Iyy*Gdoy[i] - K2*(Oy[i]-Goy[i])
Gz[i]=(Iyy-Ixx)*Ox[i]*Oy[i] + (-TheE[i]*math.sin(Phi[i])+PsiE[i]*math.cos(Phi[i])*math.cos(The[i]))-K2*Oz[i-1] + Izz*Gdoz[i] - K2*(Oz[i]-Goz[i])
GxTotal=GxTotal+Gx[i]
GyTotal=GyTotal+Gx[i]
GzTotal=GzTotal+Gx[i]
Dox[i]=(Gx[i]-(Izz-Iyy)*Oy[i]*Oz[i])/Ixx
Doy[i]=(Gy[i]-(Ixx-Izz)*Ox[i]*Oz[i])/Iyy
Doz[i]=(Gz[i]-(Iyy-Ixx)*Ox[i]*Oy[i])/Izz
Phi[i+1]=Phi[i]+DeltaT*Dphi[i]
The[i+1]=The[i]+DeltaT*Dthe[i]
Psi[i+1]=Psi[i]+DeltaT*Dpsi[i]
Ox[i+1]=Ox[i]+DeltaT*Dox[i]
Oy[i+1]=Oy[i]+DeltaT*Doy[i]
Oz[i+1]=Oz[i]+DeltaT*Doz[i]
fig,ax=plt.subplots()
ax.plot(Phi,label='phi', color = 'r')
ax.plot(The,label='the', color = 'b')
ax.plot(Psi,label='psi', color = 'g')
ax.axhline(PhiF, color = 'r', linewidth = 0.5)
ax.axhline(TheF, color = 'b', linewidth = 0.5)
ax.axhline(PsiF, color = 'g', linewidth = 0.5)
ax.set_title('オイラー角の時間履歴',fontname='MS Gothic')
ax.set_xlabel('経過時間(/10 s)',fontname='MS Gothic')
ax.set_ylabel('オイラー角(rad),細線は目標値',fontname='MS Gothic')
plot_set(ax,'best')
fig,ax2=plt.subplots()
ax2.plot(PhiE,label='phiE', color = 'r')
ax2.plot(TheE,label='theE', color = 'b')
ax2.plot(PsiE,label='psiE', color = 'g')
ax2.set_title('オイラー角の誤差の時間履歴',fontname='MS Gothic')
ax2.set_xlabel('経過時間(/10 s)',fontname='MS Gothic')
ax2.set_ylabel('オイラー角の誤差(*10 rad/s),細線は目標値',fontname='MS Gothic')
plot_set(ax2, 'best')
fig,ax3=plt.subplots()
ax3.plot(Dphi,label='Dphi', color = 'r')
ax3.plot(Dthe,label='Dthe', color = 'b')
ax3.plot(Dpsi,label='Dpsi', color = 'g')
ax3.set_title('オイラー角の微分の時間履歴',fontname='MS Gothic')
ax3.set_xlabel('経過時間(/10 s)',fontname='MS Gothic')
ax3.set_ylabel('オイラー角の微分(*10 rad/s),細線は目標値',fontname='MS Gothic')
plot_set(ax3,'best')
fig,ax4=plt.subplots()
ax4.plot(Gx,label='Gx')
ax4.plot(Gy,label='Gy')
ax4.plot(Gz,label='Gz')
ax4.set_title('入力の時間履歴',fontname='MS Gothic')
ax4.set_xlabel('経過時間(/10 s)',fontname='MS Gothic')
ax4.set_ylabel('入力の大きさ(N×M)',fontname='MS Gothic')
plot_set(ax4,'best')
plt.show()
print('GxTotal',GxTotal,'GyTotal',GyTotal,'GzTotal',GzTotal)
#計算時間の図示
print('computing time is ',time.time()-start)
print('finish')
## 最後に
M1の冬に結構苦戦しながら書いたレポートだったので、世に出せてよかったです。まだまだ投稿したいネタがたくさんあるので、これからも逐次投稿していきたいです。LinkedinとFacebookやってる(これから充実させていきたい)ので、もしよければフォローお願いします!