はじめに
前回の記事では、p5.js を使って「リンク機構の軌跡」を描画するプログラムを紹介しました。
しかし、リンク機構の構造上「無理な配置」が3パターン存在します。その無理な配置を考慮して、ドラッグ機能を追加したいと思います。
可動領域について
この関数は、2点 A, B から決まった長さの棒をそれぞれ伸ばして交差する点を求める関数です。コンパスを2回使って円を描き、交点を求める ようなイメージです。
/**
* 2点A, Bからそれぞれ異なる長さ r1, r2 で伸ばす棒が交差する点を求める
* @param {p5.Vector} A - 棒1の起点
* @param {p5.Vector} B - 棒2の起点
* @param {number} r1 - 棒1の長さ
* @param {number} r2 - 棒2の長さ
* @param {boolean} useUpper - trueで上側交点、falseで下側交点を返す
* @returns {p5.Vector|null} - 交差点(上側)、なければ null
*/
function getFixedLengthJointDual(A, B, r1, r2, useUpper = true) {
let d = dist(A.x, A.y, B.x, B.y);
if (d > r1 + r2 || d < abs(r1 - r2) || d === 0) return null;
let dx = (B.x - A.x) / d;
let dy = (B.y - A.y) / d;
// 三角形の底辺から高さ h を計算(余弦定理の派生)
let a = (r1 * r1 - r2 * r2 + d * d) / (2 * d);
let h = Math.sqrt(r1 * r1 - a * a);
// 中点からのベース位置(交差線の直下)
let px = A.x + a * dx;
let py = A.y + a * dy;
// 垂直ベクトル(上側を選択)
let nx = -dy;
let ny = dx;
// 上側 or 下側を選んで返す
let sign = useUpper ? 1 : -1;
return createVector(px + sign * h * nx, py + sign * h * ny);
}
下記がエラーを回避するためのチェックロジックです。このプログラムの、3つの判定条件 がプログラムの異常停止を防いでいます。それぞれの条件について説明していきたいと思います。
if (d > r1 + r2 || d < abs(r1 - r2) || d === 0) return null;
条件1: d > r1 + r2
d > r1 + r2は 関節部分が 離れすぎて交差できない場合の状態です。
明らかに、点Bから点Cまでの距離が足りません。

条件2: d < abs(r1 - r2)
d < abs(r1 - r2) は 関節部分が近すぎて交差できない場合の状態です。
点A・Bが下のような配置の場合、物理的に不可能な配置になってしまい点Cが配置できません。
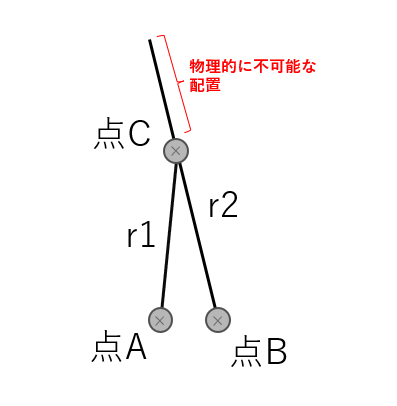
条件3: d === 0
d === 0は、同一点から交差しようとしている場合の状態です。
これは、AとBが同じ座標だった場合。つまり、同じ長さの線でしかありえない状態ですが、交差する点が複数パターン存在するため、一つに結果を絞り込むのは不可能です。

ドラッグ機能追加
3つの判定条件を考慮して、画面上でドラッグしてもエラーにならないようにします。
ドラッグ機能実装
前回の記事で作成したクラスに、ドラック時の処理を追加しました。
/**
* 回転する線を表すクラス
*/
class RotatingLine {
//...
// ドラッグ開始判定
isMouseOver() {
return dist(mouseX, mouseY, this.cx, this.cy) < 12;
}
// ドラッグ開始
startDrag() {
this.dragging = true;
this.offsetX = this.cx - mouseX;
this.offsetY = this.cy - mouseY;
// ドラッグ開始位置を保存
this.startDragX = this.cx;
this.startDragY = this.cy;
}
// ドラッグ中
drag() {
if (this.dragging) {
this.cx = mouseX + this.offsetX;
this.cy = mouseY + this.offsetY;
}
}
// ドラッグ終了
endDrag() {
this.dragging = false;
// ドラッグ中に可達性チェック
if (!checkReachability()) {
// 不可達なら元の位置に戻す
this.cx = this.startDragX;
this.cy = this.startDragY;
}
}
}
判定条件
いままで説明した3つの判定条件は、現在の位置関係によるチェックなので、回転する前から回転後を予測した判定式に書き換えて実装していきます。
/**
* 現在の構造が物理的に成立するかどうかをチェックする
* @returns {boolean} - 成立するならtrue、しないならfalse
*/
function checkReachability() {
let endPointA = rotatingLine1.getEndPoint();
let endPointB = rotatingLine2.getEndPoint();
let centerA = createVector(rotatingLine1.cx, rotatingLine1.cy);
let centerB = createVector(rotatingLine2.cx, rotatingLine2.cy);
let lengthACenter = p5.Vector.dist(endPointA, centerA);
let lengthBCenter = p5.Vector.dist(centerA, centerB);
let centerToCenter = p5.Vector.dist(centerB, endPointB);
let jointPoint = getFixedLengthJointDual(endPointA, endPointB, connectingLine1.length, connectingLine2.length, false);
if (!jointPoint) {
console.log("リンクの交点が存在しない");
return false;
}
let lengthAJoint = p5.Vector.dist(endPointA, jointPoint);
let lengthBJoint = p5.Vector.dist(endPointB, jointPoint);
let totalByLink = lengthAJoint + lengthBJoint;
let totalByFixed = lengthACenter + lengthBCenter + centerToCenter;
let condition1 = totalByLink - totalByFixed;
let condition2 = lengthACenter + Math.abs(lengthAJoint - lengthBJoint) + centerToCenter < lengthBCenter;
return condition1 > 0 && condition2;
}
右側の回転軸をドラッグしたときに、有効な可動領域(白色) を表示しています。

| 範囲 | 内容 |
|---|---|
| 白色 | ドラッグが可能な領域 |
| 外側グレー | ドラッグが不可な領域(条件1を対策) |
| 内側グレー | ドラッグが不可な領域(条件2, 3を対策) |
外側の判定方法
「回転軸A → 点A → 点C(交点)→ 点B → 回転軸B」という、赤い線の合計距離よりも長くなってしまう位置は、外側のグレー領域として判定します。
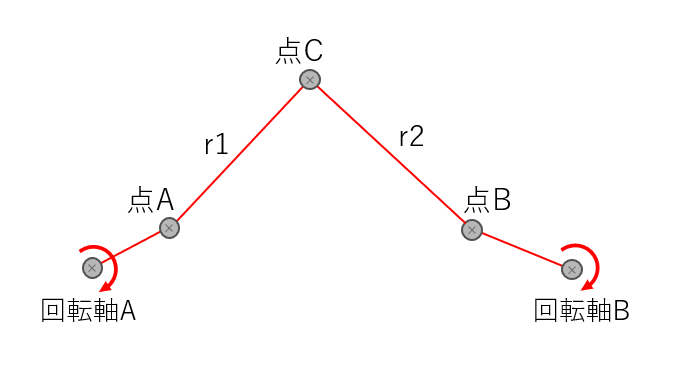
内側の判定方法
「点A → 回転軸A → 回転軸B → 点B」という赤い線の合計距離よりも短くなってしまう場合は、内側のグレー領域として判定します。

完成
これで、画面上でドラッグしても、エラーになるならないように実装できました。
おわりに
今回は、だいぶマニアックな内容でしたがこのような判定ロジックは考えるのが楽しいですね。
バックエンド側のエラーの対処だけではなく、フロントエンド側のUI・UXの対処も重要だということも分かりましたね。
GitHubのリポジトリも日々更新しているので興味のある方は、覗いてみてください。
ここまで読んで頂きありがとうございました。

