LSGAN(Least Square Generative Adversarial Networks)を試してみた

はじめに

最近、**Least Squares Generative Adversarial Networks**を読んだので、Pytorchで実装してみました。本当はアニメ顔生成モデルを作りたかったのですが、ローカルのスペックでは厳しそうだったのでMNISTによる追試しかできていませんが...

画像処理初学者で、学習したことのまとめがてら記事を書いているので、間違いがあるかもしれません。その際はご指摘ください。

GANについて

生成モデル

訓練データを学習し、それらのデータと似たような新しいデータを生成するモデルのことを生成モデルと呼びます。別の言い方をすると、訓練データの分布と生成データの分布が一致するように学習していくようなモデルです。GANはこの生成モデルの一種です。

学習の仕組み

GANはGeneratorとDiscriminatorという２つのネットワークから成り立ちます。Generatorは訓練データと同じようなデータを生成しようとします。一方、Discriminatorはデータが訓練データ(real sample)なのか、それともGeneratorが生成したもの(fake sample)なのかを識別します。

GeneratorはDiscriminatorに本物と識別させれるように、Discriminatorは正しく正誤を判断できるようにと、2つのネットワークを同時に更新していくことによって、生成モデルを学習させていきます。

LSGANについて

学習の仕組みと目的関数

それでは、数式を用いてLSGANの仕組みを見ていきます。

$G$はgenerator、$D$はdiscriminator、$x$は訓練データ、$z$はノイズを表します。

$G$はノイズ$z$を入力としてデータを生成します。$D(x)$は、そのデータが訓練データである確率を表します。$D$は訓練データと生成データに対して正しくラベル付けを行う確率を最大化しようとします。一方、$G$は誤差を最小化しようとします。

LSGANは正解ラベルに対する二乗誤差を用いるので、目的関数はパラメータ$a, b, c$を用いて以下のように表せます。

$ min_D L(D) = \frac{1}{2} E[(D(x) - b)^2] + \frac{1}{2} E[(D(G(z)) - a)^2]$

$ min_G L(G) = \frac{1}{2} E[(D(G(z)) - c)^2]$

($a,b,c$は定数であり設計者が事前に決めておくそうなのですが、論文では$a,b,c=−1,1,0$または$a,b,c=0,1,1$が推奨されています。)

$D$の精度が向上すると$D(x)$が大きくなり、$L(D)$の第1項が大きくなります。従って$D(G(z))$は小さくなるため、$L(D)$の第2項も大きくなります。

一方、$G$が訓練データに似ているものを生成できるようになると、$D$がうまく分類できなくなるため$D(G(z))$は大きくなり、$L(G)$は小さくなるという構造になっています。

誤差関数に最小二乗を用いるメリット

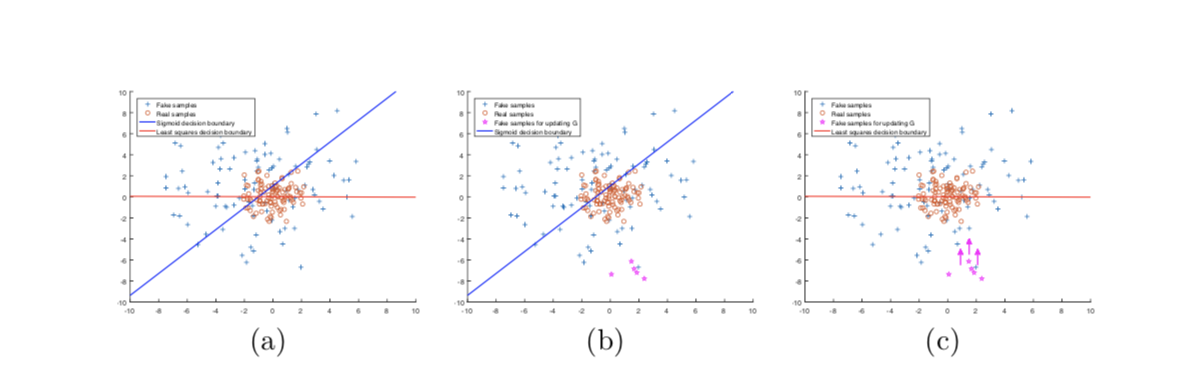
上図の$(b)$がシグモイドクロスエントロピー誤差の決定境界、$(c)$が最小二乗誤差を用いた際の決定境界を示しています。$G$を更新する際のfake sampleがマゼンタ色の点です。

$(b)$のようにシグモイドクロスエントロピー誤差を用いて更新をすると、fake sampleは決定境界の正しい側にあるため、誤差は非常に小さな値になってしまいます。
しかし，$(c)$のように、最小二乗誤差を用いて更新をすると、決定境界の正しい側でも、遠くにあるサンプルにはペナルティを課すため、fake sample(Generatorが作成したデータ)を決定境界に向かって移動させることができます。

よって、Generatorは決定境界に沿うようにfake sampleを生成するように誤差を最小化することができるといったものです。単純ではありますが、非常に強力です。

モデルの構造

それでは、実装に移っていきます。

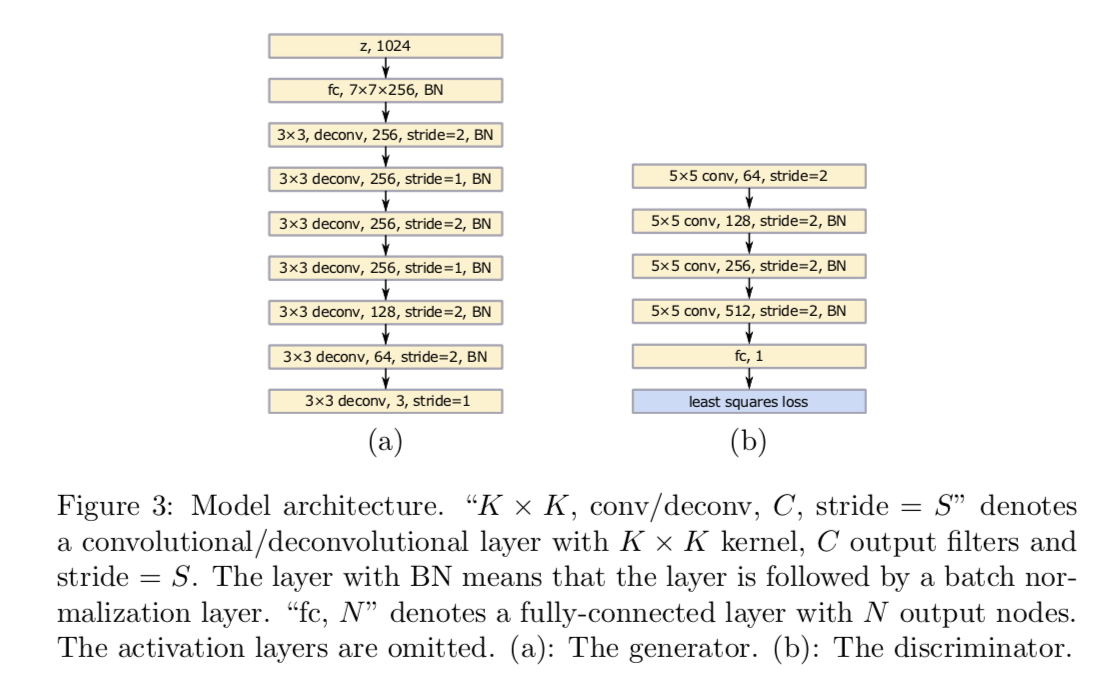
モデルの構造は上図のようになっています。注意すべき点は、中間層においてバッチノーマライゼーションを適用していることと(DCGANと同じです)、今回は畳み込み層を減らしていること、またMNISTを学習データとして用いているので、出力は1次元であるということです。

実装

モデルの実装

上図にしたがってモデルを定義していきます。まずはGeneratorから。
(今回はlatent spaceの次元を62次元にしました)

import torch
import torch.nn as nn
import torch.functional as F

class Generator(nn.Module):
    
    def __init__(self):
        super(Generator, self).__init__()
        # fully connected
        self.fc = nn.Sequential(
            nn.Linear(62, 1024),
            nn.BatchNorm1d(1024),
            nn.LeakyReLU(),
            nn.Linear(1024, 128 * 7 * 7),
            nn.BatchNorm1d(128 * 7 * 7),
            nn.LeakyReLU(),
        )
        # deconvolutional layer
        self.deconv = nn.Sequential(
            nn.ConvTranspose2d(128, 64, kernel_size=4, stride=2, padding=1),
            nn.BatchNorm2d(64),
            nn.LeakyReLU(),
            nn.ConvTranspose2d(64, 1, kernel_size=4, stride=2, padding=1),
            nn.Sigmoid(),
        )

    def forward(self, input):
        x = self.fc(input)
        x = x.view(-1, 128, 7, 7)
        x = self.deconv(x)
        return x

Discriminatorは以下のようになります。
ただし、LSGANにおいて、Discriminatorは出力ベクトルの次元を1にし、出力には活性化関数を通しません。

class Discriminator(nn.Module):
    
    def __init__(self):
        super(Discriminator, self).__init__()
        # convolutional layer
        self.conv = nn.Sequential(
            nn.Conv2d(1, 64, kernel_size=4, stride=2, padding=1),
            nn.LeakyReLU(0.2),
            nn.Conv2d(64, 128, kernel_size=4, stride=2, padding=1),
            nn.BatchNorm2d(128),
            nn.LeakyReLU(0.2),
        )
        # fully connected
        self.fc = nn.Sequential(
            nn.Linear(128 * 7 * 7, 1024),
            nn.BatchNorm1d(1024),
            nn.LeakyReLU(0.2),
            nn.Linear(1024, 1),
            # nn.Sigmoid(),
            # lsgan not using activation function with Generator
        )
    
    def forward(self, input):
        x = self.conv(input)
        x = x.view(-1, 128 * 7 * 7)
        x = self.fc(x)
        return x

これでモデルが完成しました。それでは、学習の過程をコードに落としていきます。

学習過程の実装

まず、LAGANの目的関数は以下のようになります。

D_loss = 0.5 * (torch.sum((D_true - b) ** 2) + torch.sum((D_fake - a) ** 2)) / batchsize
G_loss = 0.5 * (torch.sum((D_fake - c) ** 2)) / batchsize

ただし

a, b, c = 0, 1, 1

これを誤差関数として、パラメータの更新を行います。
Discriminatorの更新は以下のようになります。

# latent spaceからランダムサンプリング
# これがGeneratorの生成画像の素になります
z = torch.rand(batch_size, z_dim)

D_optimizer.zero_grad()

# real sampleの誤差を算出
D_real = D(real_img)
D_real_loss = torch.sum((D_real - b) ** 2)

# fake sampleの誤差を算出
fake_img = G(z)
D_fake = D(fake_img.detach())  # stop back propagate to G
D_fake_loss = torch.sum((D_fake - a) ** 2)

# minimizing loss
D_loss = 0.5 * (D_real_loss + D_fake_loss) / batch_size  # lsganの目的関数
D_loss.backward()
D_optimizer.step()
D_running_loss += D_loss.data.item()

Generatorも同様、以下の様になります。

z = torch.rand(batch_size, z_dim)

G_optimizer.zero_grad()

fake_img = G(z)
D_fake = D(fake_img)

G_loss = 0.5 * (torch.sum((D_fake - c) ** 2)) / batch_size
G_loss.backward()
G_optimizer.step()
G_running_loss += G_loss.data.item()

これを訓練ループとして定義します。

import torch.optim as optim
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
from torchvision.utils import save_image

def train(D, G, train_itr, epoch, batch_size=128, z_dim=62):
    
    # settings
    D_optimizer = optim.Adam(D.parameters(), lr=0.0002 ,betas=(0.5, 0.999))
    G_optimizer = optim.Adam(G.parameters(), lr=0.0002 ,betas=(0.5, 0.999))
    
    # labels
    a = 0
    b = 1
    c = 1

    for i in range(epoch):

        # answer labels
        y_real = torch.ones(batch_size, 1)
        y_fake = torch.zeros(batch_size, 1)

        D_running_loss = 0
        G_running_loss = 0

        for batch_index, (real_img, _) in enumerate(train_itr):

            if real_img.size()[0] != batch_size:
                break

            # random sampling from latent space
            z = torch.rand(batch_size, z_dim)

            # --------------------
            # update discriminator
            # --------------------

            D_optimizer.zero_grad()

            # real
            D_real = D(real_img)
            D_real_loss = torch.sum((D_real - b) ** 2)

            # fake
            fake_img = G(z)
            D_fake = D(fake_img.detach())  # stop back propagate to G
            D_fake_loss = torch.sum((D_fake - a) ** 2)

            # minimizing loss
            D_loss = 0.5 * (D_real_loss + D_fake_loss) / batch_size
            D_loss.backward()
            D_optimizer.step()
            D_running_loss += D_loss.data.item()

            # ----------------
            # update generator
            # ----------------
            
            G_optimizer.zero_grad()

            fake_img = G(z)
            D_fake = D(fake_img)
            
            G_loss = 0.5 * (torch.sum((D_fake - c) ** 2)) / batch_size
            G_loss.backward()
            G_optimizer.step()
            G_running_loss += G_loss.data.item()

        print('epoch: %d loss_d: %.3f loss_g: %.3f' % (i + 1, D_running_loss / batch_size, G_running_loss / batch_size))

        # save image
        save_image(fake_img, save_place, nrow=16, normalize=True)

    torch.save(G.state_dict(), save_place)
    torch.save(D.state_dict(), save_place)

データセット

今回はMNISTのデータを使います。pytorchのライブラリにデータがあるので、それを使います。

# dataset
transform = transforms.Compose([
    transforms.ToTensor()
])
dataset = datasets.MNIST('data/mnist', train=True, download=True, transform=transform)
train_itr = DataLoader(dataset, batch_size=batch_size, shuffle=True)

学習

それでは、学習を開始します。

# args
z_dim = 62
epoch = arg.epoch
batch_size = arg.batch_size

# initialize modules
D = Discriminator()
G = Generator()

train(D, G, train_itr, epoch, batch_size, z_dim)

結果

epoch 1

epoch 15

epoch 30

おわりに

30回ほどで本物とほぼ見分けのつかない画像が生成されました。びっくり。
本当はアニメ顔の生成をしたかったので、以降、豊富な計算資源を手に入れたらネットワークを大きくして、試してみたいと思います。

あと、Least Squaresの利点にわざわざ言及しておきながら他の誤差関数を用いた学習との比較をしていません。(すみません)
詳しくは論文: Least Squares Generative Adversarial Networksに書いてあるので、気になるかたはそちらをご覧ください。