計量経済学を勉強している中で,制限従属変数の推定で出てくるミルズ比でちょっとつまずいたのでメモ.
データの性質
分析の対象となる従属変数(被説明変数)がある水準を境に切り取られている場合を一般的に制限従属変数と呼びます.
こういったデータの理由としては次の2点が考えられます.
- 端点解
- データが何らかの理由で完全に集められていない場合
- 切断: 被説明変数も説明変数も共にかけている場合
- 打ち切り: 説明変数は完全だが,被説明変数がかけている場合
こういったデータに対する推定は,通常の方法では多くの場合でパラメータの推定量にはバイアスが生じてしまいます.
それらに対し,モデリングを行う際に用いる手法としてあげられるのが,前者の端点解の場合,以下で説明をするトービットモデルや,後者のデータ収集の際のセレクションバイアスがある場合はヘックマンの2段階推定法などがあります.(今回は前者に限定して考えていきます)
トービットモデル
トービットモデルは...
トービット・モデルはTobin(1958)で初めて論じられ、Goldberger(1964)によってトービットと命名され、一般に広く紹介されるようになった。Amemiya(1985,Chapter10)やMaddala(1983,Chapter6)で包括的にサーベイされている。
らしいです.元論文をわざわざ読む気にもなれなかったので引用.
例えば,所得が一定水準を超えると海外旅行をすると考えられる時に,一定水準以下の家計も含めた全サンプルの海外旅行の需要関数を推定したいとします.その時,通常の最小二乗法で推定すると,データの分布の端がある水準で切断されており,誤差項が正規分布せず,推定量にバイアスが生じてしまいます.こんなケースに使えるのがトービットモデルになります.
それではトービットモデルをみていきます.
まず,以下のような$y$の潜在変数$y^*$について考えます.ここで回帰式はOLSの仮定を満たしているものとします.
\begin{align}
y^* &= X \beta + u \\
y &= max(y^*, 0)
\end{align}
たとえば,$y^* ∼ N(100,100)$, $threshold=0$のときは以下のような感じになります.$y^*$が$0$のところで打ち切られ,それ以下の値はすべて$0$に貼り付いているようなっています.
import math
import numpy as np
import matplotlib.pyplot as plt
sigma, mu = 100, 100
threshold = 0
normdist = lambda x: 1/np.sqrt(2*np.pi*sigma)*np.exp(-1*((x-mu)**2)/(2*(sigma**2))) if x > 0 else 0
x = list(range(-200, 401))
y = list(map(normdist, x))
plt.plot(x, y)
plt.xlabel('Y')
plt.show()
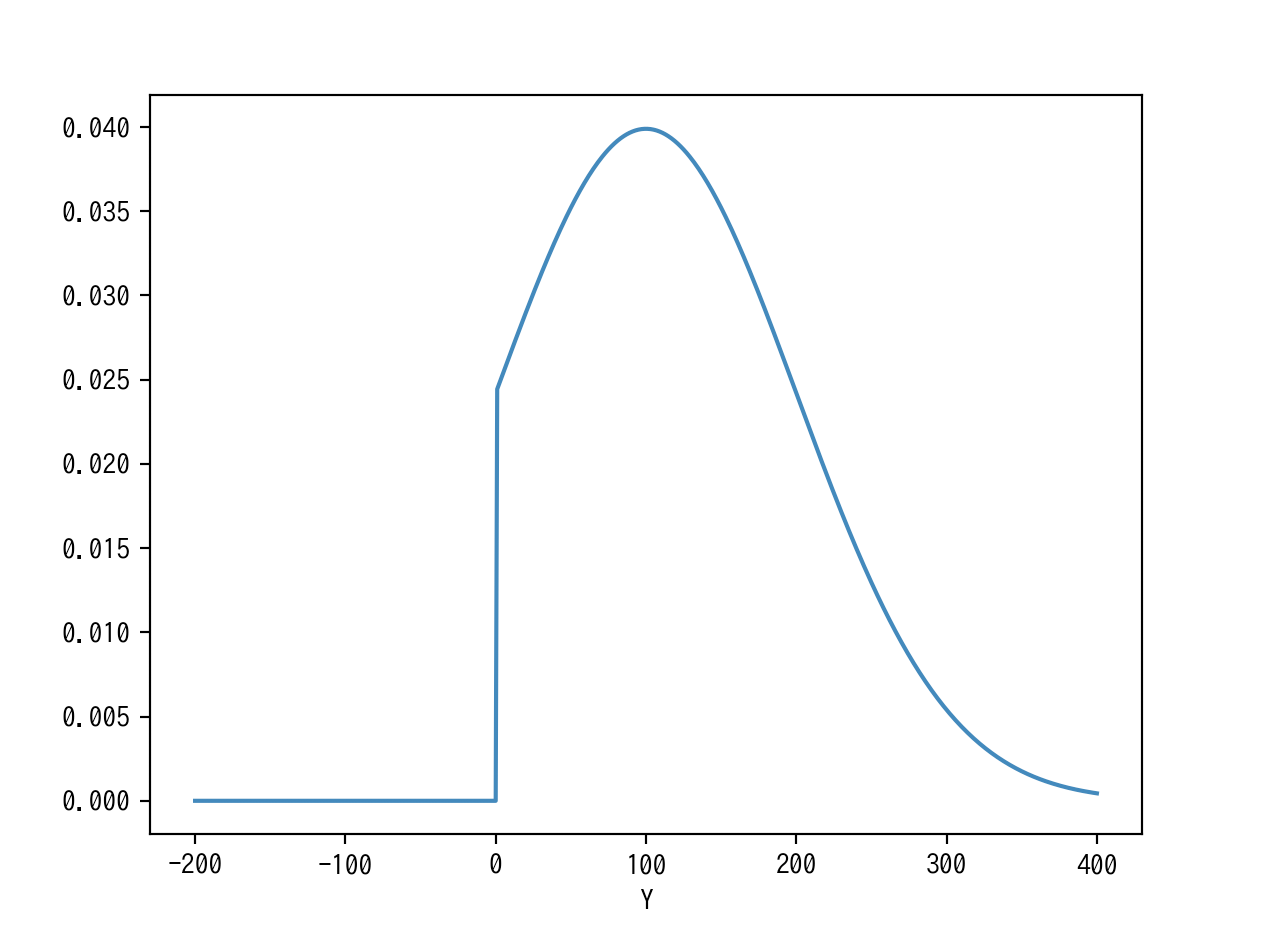
$threshold = 0$としたときの,$y$の条件付き期待値は以下のようになります.
$$E(y \ | \ X) = P(y^* > 0 \ | \ X_i)E(y \ | \ y^* > 0, X_i) + [1 - P(y > 0 \ | \ X)] \times 0$$
このとき,$\Phi$を正規分布の密度関数として
$y>0$となる確率は,$P(y > 0) = \Phi (\frac{X \beta}{\sigma})$となります.
また,$y = 0$となる確率は$P(y^* < 0 \ | \ X) = P(u < -X \beta \ | \ x) = P(\frac{u}{\sigma} < - \frac{X \beta}{\sigma} \ | \ x) = 1 - \Phi(\frac{X \beta}{\sigma})$となっていることを確認できます.
ここで,$y^* > 0$の時の$y$の期待値を回帰することを考えます.このとき,$y$そのものは正規分布していないので,推定量はBLUE(Best Linear Unbiased Estimator)となりません.そこで,閾値の超え易さを考慮して推定してあげるというのがこのモデルの発想です.
さて,$y^* > 0$の場合の$Y$の条件付き期待値は,以下のように表すことができます.ここで,$\phi$は密度関数,$\Phi$は分布関数です.
\begin{aligned}
E(y | y^* > 0, X) &= E(y | X \beta + u > 0) \\
&= E(y | u > -X \beta) \\
&= X \beta + E(u | u > -X \beta) \\
&= X \beta + \sigma E(u / \sigma | u / \sigma > -X \beta / \sigma) \\
&= X \beta + \sigma \frac{\phi(X \beta / \sigma)}{\Phi(X \beta / \sigma)} \end{aligned}
ここで上式の右辺第2項に出てきているものを,$\lambda(X \beta/ \sigma) = \phi(X \beta/ \sigma) / \Phi(X \beta/ \sigma)$とおきます.この$\lambda$が本題の**逆ミルズ比(inverse Mills ratio)**です.
導出過程を追っていればなぜ出てきたのかわかりますが,(僕は頭が悪いので)これが何を表しているのかわかりませんでした.このミルズ比はなにを表しているのでしょうか.
逆ミルズ比
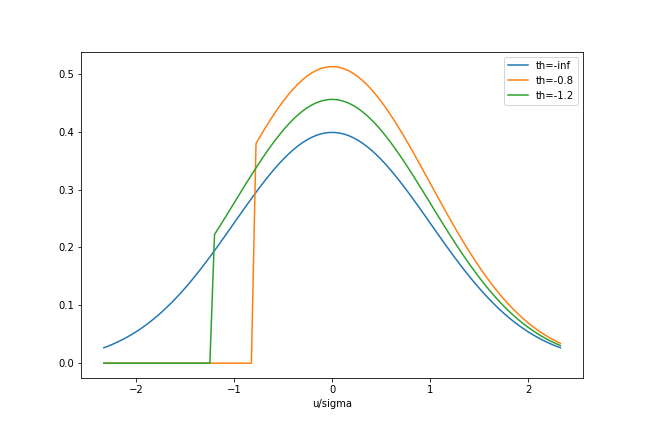
まず,先の式の誤差の条件付き期待値($ E(u / \sigma | u / \sigma > -X \beta / \sigma)$),$u / \sigma$を$-X \beta / \sigma$で打ち切ったときの$u / \sigma$切断正規分布の形状は以下のようになっていることを確認します.
import numpy as np
from scipy.stats import norm, truncnorm
import matplotlib.pyplot as plt
th = -0.8
fig, ax = plt.subplots(figsize=(9,6))
# norm
x = np.linspace(norm.ppf(0.01),norm.ppf(0.99),100)
y = norm.pdf(x)
ax.plot(x,y,label='th=-inf')
y = truncnorm(th, norm.ppf(0.99)).pdf(x)
ax.plot(x,y,label='th=-0.8')
th = -1.2
y = truncnorm(th, norm.ppf(0.99)).pdf(x)
ax.plot(x,y,label='th=-1.2')
plt.xlabel('u/sigma')
ax.legend()
青色の線が通常の正規分布,橙色の線が$threshold = -0.8$緑色の線が$threshold = -1.2$となっています.
標準正規分布を$−X \beta / \sigma$で打ち切ったとき,切断正規分布の条件つき期待値$E(u|u > −X \beta)$は,打ち切りが起こるところ($−X \beta / \sigma$)までの面積($\Phi(−X \beta / \sigma)$)で密度関数$\phi(u/ \sigma)$を割った値となっています.
この切断正規分布から,$−X \beta$を大きくするほど($X \beta$を小さくするほど)打ち切り部分に含まれる$\phi(u/ \sigma)$の面積$\Phi(u/ \sigma)$は広くなっていくわけなので,打ち切りが起こりやすくなっていることがわかります.またその結果,条件つき期待値$E(u | u > −X \beta)$は大きくなっていくことがわかります.このときは,もともとの密度関数$\phi(u/ \sigma)$からかなりずれた状態になっています.
逆に,$−X \beta$を小さくするほど打ち切り部分に含まれる$\phi(u/ \sigma)$の面積$\Phi(u/ \sigma)$は狭くなっていくわけなので,打ち切りが起こりにくくなっているといえます.またその結果,条件つき期待値$E(u | u > −Xi \beta)$は小さくなっていくことがわかります.このときは,もともとの密度関数$\phi(u/σ)$に近い状態にあることがわかります.
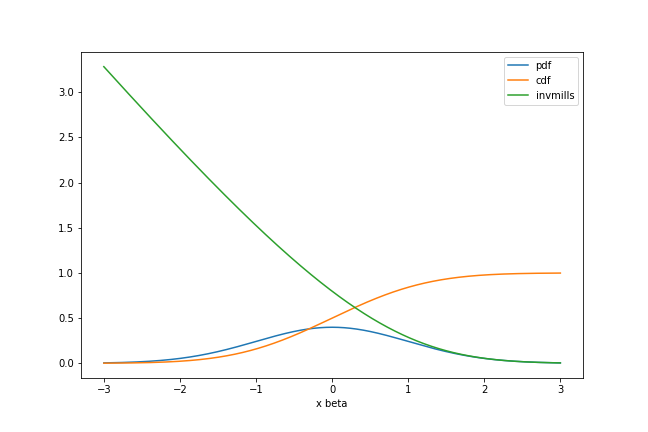
あとは$X \beta$の値,つまりこれまで閾値として扱ってきたものを正負反転させたもの$-threshold$を変化させたときに,密度関数を分布関数で除した逆ミルズ比$\lambda (X \beta / \sigma)$(すなわち,条件つき期待値$E(u | u > −X \beta)$)がどのような挙動を示すかを見てみましょう.
import numpy as np
from scipy.stats import norm, truncnorm
import matplotlib.pyplot as plt
th = -0.8
fig, ax = plt.subplots(figsize=(9,6))
# norm
x = np.linspace(-3,3,1000)
y = norm.pdf(x)
ax.plot(x,y,label='pdf')
y = norm.cdf(x)
ax.plot(x,y,label='cdf')
y = norm.pdf(x) / norm.cdf(x)
ax.plot(x,y,label='invmills')
ax.legend()
plt.xlabel('x beta')
plt.show()
一見してわかるとおり,$\lambda (X \beta / \sigma)$は,$X \beta$が正の方向に大きくなるほど$0$に近づき,負の方向に大きくなるほど$0$から離れていきます.
先に述べたとおり,$X \beta$が大きくなるとはすなわち,打ち切りが起こりにくくなることを意味していました.ということは,逆ミルズ比$\lambda (X \beta / \sigma)$は,打ち切りの起こりやすさを表していると読むことができます.
逆ミルズ比の直感的な理解
これまでやってきたことをまとめると以下のようになります.
$X \beta$が大きくなる
$\Longleftrightarrow$逆ミルズ比$\lambda (X \beta / \sigma)$が$0$に近づく
$\Longleftrightarrow$打ち切りが起こりにくくなり,その結果条件つき期待値$E(u | u > −X \beta)$が小さくなる
$X \beta$が小さくなる
$\Longleftrightarrow$逆ミルズ比$\lambda(X \beta / \sigma)$が$0$から遠ざかる
$\Longleftrightarrow$打ち切りが起こりやすくなり,その結果条件つき期待値$E(u | u > −X \beta)$が大きくなる
よって,逆ミルズ比は,打ち切りの起こりやすさを制御しているものと解釈できます.