Python3ではじめるシステムトレード：ブラック-ショールズ方程式を理解する

　オプションの理論価格を算出するブラックショールズ方程式について調べてみました。

　サンプルを動かすにはPCにPythonがインストールされている必要があります。まだインストールされていない方はJupyter notebookのインストールを参照してください。

オプション取引

　コールオプションは、あらかじめ定められた金融商品(原資産)をあらかじめ定められた期間（満期)にあらかじめ定められた価格（行使価格)で買う権利をあたえる金融商品です。プットオプションは同じ仕組みを用いて、売る権利をあたえます。原資産を株式や為替レートとしたものが活発に取引されています。売買する権利が満期のみに与えられているものをヨーロピアンオプション、満期前であればいつでも権利を行使できるものをアメリカンオプションといいます。

モデル化

　株価の動きはよく酔っ払いの千鳥足にたとえられます。酔っ払いは予測のつかない歩き方をするからです。このような歩みをランダムウォークと言います。数学的にもっとも単純なランダムウォークは、直線上を右に左に動く点で表現されます。最初の点の位置をゼロとすると、この点は時間の経過とともに同じ確率でプラスまたはマイナス方向に位置を変えます。このとき、動く距離は１とします。1つ1つの動きは+1または-1という値で表現できます。たまたま+1が2回続くと、位置はゼロからまずは1に,そして2へと変化します。しかし、どこに行くかは事前にはわかりません。このように将来の位置がどこにいるかわからない、無作為に確率的に動きが決定される運動をランダムウォークといいます。株価の動きはランダムウォークとしてモデル化されるのです。
　確率的に決定される変数を確率変数といいます。また、時間の変化とともに変化する確率変数のモデルを確率過程といいます。株価の動きは確率過程としてモデル化されていることになります。

幾何ブラウン運動

　原資産である株式の価格を連続した値をとる確率過程として表現することもできます。ここでは幾何ブラウン運動という特殊な動きを想定してモデル化していきます。それは

$\mathrm{d}S_t=\mu S_t \mathrm{d}t+\sigma \sqrt{\mathrm{d}t} S_t\mathrm{d}W_t$　(1)

の確率微分方程式であらわされます。$S_t$は$t$時点の株価です。$\sigma$は価格変動の程度を$\mu$は株価のトレンドをあらわす定数です。$W_t$は標準ウィナー過程です。$\mathrm{d}W_t$は標準正規分布にしたがいます。$\mu$も$\sigma$も株価がもつ特有の特性で、過去の価格データから推定されます。このモデルを伊藤の公式を用いて、対数価格のモデルへと変数変換します。

$S_{t+1}=S_{t}\exp[(\mu-0.5\sigma^2)\mathrm{d}t+\sigma \sqrt{\mathrm{d}t}\mathrm{d} W_t]$

両辺の対数をとると

$d \ln S_{t+1}=(\mu-0.5\sigma^2)\mathrm{d}t+\sigma\sqrt{\mathrm{d}t}\mathrm{d} W_t$

となるので、対数価格のモデルだとわかります。この幾何ブラウン運動をPythonを使って人工的に作ってみましょう。

　リターンの年率($\mu$)を１０％とし、ボラティリティーと呼ばれる年率換算の標準偏差は40%とします。これは典型的な個別株の動きです。この株式の一日の終値を250回生成しそれを１年の株価の動きとします。それを1,000,000回繰り返します。さらに、株価の動きとはべつに$\mu$(ドリフト)項の動きも保存しておきます。乱数を生成するランダムジェネレーターとしてPCG64を使用しています。これはPythonの新しい機能です。

import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.stats import lognorm
from scipy import stats
from numpy.random import Generator, PCG64, MT19937
import numpy as np

def genS(mu,sigma0,nDays,nSim):
    #np.random.seed(1)
    sigma = np.array([sigma0])
    dt = 1/nDays
    S = np.array([[0.0 for i in range(nDays)] for j in range(nSim)])
    M = np.array([[0.0 for i in range(nDays)] for j in range(nSim)])
    rng = Generator(PCG64())#MT19937()) PCG64かMT19937(メルセンヌツイスター)を使用。
    for j in range(nSim):
        w=rng.standard_normal( size=(1,nDays)).T
        x = np.exp((mu - sigma ** 2 / 2) * dt + w)
        x = np.vstack([np.ones(len(sigma)), x])
        x = x.cumprod(axis=0)
        m = np.exp(w)
        m = np.vstack([np.ones(len(sigma)), m])
        m = m.cumprod(axis=0)
    
        S[j][:]=x.ravel()
        M[j][:]=(x-m).ravel()
    return S,M
S,M=genS(0.1,0.4,250,1000000)

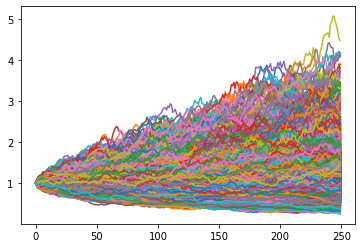
まず、株価の動きを見ていきましょう。つぎの図は生成された株価の動きをプロットしたものです。

for i in S:
    plt.plot(i)

ランダムウォークというと期待値の周りを行ったり来たりするというイメージがあるかもしれませんが、動きは上下に大きく振れるときもあります。株価の動きを注意深くみていきましょう。株価の動きは時間の経過とともに振れ幅が大きくなっています。これは初期値と$t$時点での株価の差の分散が時間の経過とともに大きくなっていることを意味します。

ドリフト

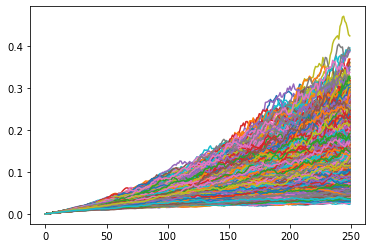
　つぎにドリフトの部分を見てみましょう。上述の幾何ブラウン運動の$\mu$に着目しましょう。これは確定的トレンドと解釈できます。ただしこれはリターンとして考えた場合です。株価でみると$\mu$の影響は各$t$時点での株価に左右されます。したがって、ドリフトと呼ばれるこの動きは確率過程の一部です。まずそれを確かめてみましょう。

for i in M:
    plt.plot(i)

こちらは線形の確定的なトレンドをもっているように見えますが、実はランダムな動きをしています。その証拠に1000000回の試行のどれもが独自の動きをしています。これは株価の変動が$\mu$の結果に影響を与えているからです。一般的に見られる

$S_t=S_{t-1}+\mu\mathrm{d}t+\sigma\sqrt{\mathrm{d}t} \mathrm{d}W_t$
で表現されるドリフト項付きの株価モデルの動きとは異なります。こちらは確定的トレンドの項をもちます。

　初期値と$t$時点での株価の差の期待値も時間の経過とともに大きくなります。

確率トレンド(確率ドリフト)

また、株価の動きにはドリフト項が作るトレンド以上に強いトレンドが出ているものがあります。これはランダム項の影響です。生成された乱数の多くが正(負)の値であったために作られたトレンドで、確率トレンド(確率ドリフト)といいます。この影響はボラティリティが大きくなるとさらに大きくなります。この確率過程ではトレンドを作るのはドリフトだけではありません。乱数の和もトレンド形成に影響しています。(注)stochastic trendの用法はさまざまあるので確認が必要です。計量経済学の分野では、時間トレンドをもつARモデルの作るトレンドであることが多いですが、ここでは乱数のつくるトレンドでマーチンゲールと同等です。

伊藤のレンマ

このような株式を原資産にもつヨーロピアンのコールオプションの満期でのペイオフを$V(S,T)$とします。このペイオフの満期前の価値を得るためには、株価と時間の変化の関数として$V(S,T)$をとらえる必要があります。伊藤のレンマを用いると$V$の価値の時間変化を表現できます。それは

$\mathrm{d}V=\left(\mu S\frac{\partial V}{\partial S}+\frac{\partial V}{\partial t}+\frac{1}{2}\sigma^2S^2 \frac{\partial^2 V}{\partial S^2}\right)\mathrm{d}t+\sigma\sqrt{\mathrm{d}t} S\frac{}{}\mathrm{d}W$ --- (2)
の確率微分方程式になります。この式は確率的項を含んでいますので、$\mathrm{d}V$の動きはランダムです。

オプション市場の仕組み

　株式市場では、同じ株式銘柄を取引したい売り手と買い手がそろって初めて取引が成立します。しかし、常に取引相手がいるとは限りません。そこで、仲介業者は、リスクに見合った報酬を得ることで取引の仲立ちをしています。オプションの取引では通常の株式の取引以上の困難があります。それは同じ株式であってもさまざまなオプションがあるからです。取引したいオプションの満期や行使価格などにバリエーションが多いということは、同じ取引の出会いの機会は減ります。それは仲介業者にとっては大きなリスクです。そこで仲介業者は仲介をするのではなく、取引相手の注文を自身で受け、そのポジションのリスクをなくす取引戦略を考えます。これをコールオプション複製(ヘッジ)戦略といいます。そしてこのヘッジ戦略にかかる費用をオプションを供給することの対価として徴収しようと考えます。この戦略はつぎのように構築します。

オプション複製戦略とブラック―ショールズの偏微分方程式

コールオプションを買いたい投資家が現れたら、そのオプションを取引相手に提供します。仲介業者(マーケットメイカ:MM)にとってはコールオプションを売ったことになります。しかし、このままではコールオプションのリスクを抱えることになります。満期に株価が行使価格を大きく上回っていたら、取引相手は買う権利を行使してきます。MMは行使価格でかれらに株式を売る必要がでてきます。しかし、MMはその株式をもっていないので、その時点で市場から時価で購入する必要があり、市場で高く買い、行使相手に安く売ることになります。これは大きな損失につながります。このようなリスクをなくすためにMMは$\partial V/ \partial S$の株価をオプション取引と同時に買っておきます。このヘッジに必要なポジション(在庫)の価値は

$\Pi=-V+\frac{\partial V}{\partial S}S$
になります。$-V$はオプションの売りポジションを示しています。しかし、時間が経過したり、株価が動いたりすると、$\partial V/ \partial S$も動いてしまいます。その変化は

$\Delta \Pi=-\Delta V+\frac{\partial \Delta V}{\partial S}\Delta S$　---- (3)
になります。(1)と(2)の式の微小変化を離散の変化に書き換えて、それを上述の式に代入すると

$\Pi= \left(-\frac{\partial V}{\partial t}-\frac{1}{2}\sigma^2S^2 \frac{\partial^2 V}{\partial S^2}\right)\Delta t$ ---(4)
となります。ここで不確定要素である$W$と$\mu$がなくなりました。リスクのないポジションになったので、そのリターンは無リスク金利になります。$\Delta t$の間のリターンは

$\Pi r\Delta t=\Delta \Pi$
になります。(3),(4)式から

$\left(-\frac{\partial V}{\partial t}-\frac{1}{2}\sigma^2S^2 \frac{\partial^2 V}{\partial S^2}\right)\Delta t=\left(-\Delta V+\frac{\partial \Delta V}{\partial S}\Delta S\right)r \Delta t$
を得ます。これを整理するとブラック-ショールズの偏微分方程式が得られます。

$\frac{\partial V}{\partial t}+\frac{1}{2}\sigma^2S^2 \frac{\partial^2 V}{\partial S^2}+r\frac{\partial \Delta V}{\partial S}\Delta S -r\Delta V =0$　　(5)

ブラック―ショールズのオプション価格の評価式

これを満期のペイオフなどの幾つかの境界条件のもとで解くとブラック-ショールのオプション価格の評価式が得られます。(5)式は拡散方程式なので定形の解き方があります。

３つの拘束条件

解く際には３つの条件を課します。１つは満期のペイオフに関するもの。残りの２つは複製戦略に関するものです。

1. 満期のペイオフ：Max(S-K,0)

2. 株価が極端に安い：満期の株価が行使価格よりも高くなる確率がゼロである場合、その価値はゼロになります。複製をする必要ななく株式の買いポジションをもつ必要がありません。したがって、ヘッジの費用はゼロです。

3. 株価が極端に高い: 満期の株価が行使価格よりも高くなる確率が100%である場合、その価値は株価そのものになります。複製をする必要がなく、株式の買いポジションを100%としていればよいのです。買いポジションの調節がなく、ヘッジの費用はゼロです。

ブラックショールズ方程式の解

解は

$C(S_t,t)=S_tN(d_1)-Ke^{-r(T-t)}N(d_2)$
です。ここで
$N(d)=\frac{1}{2\pi}\int_{-\infty}^{d}e^{-\frac{z^2}{2}}$
$d_1=\frac{\log\frac{S_t}{K}+(r+\sigma^2/2)(T-t)}{\sigma\sqrt{T-t}}$
$d_2=\frac{\log\frac{S_t}{K}+(r-\sigma^2/2)(T-t)}{\sigma\sqrt{T-t}}$
です。結果をPythonで確かめてみましょう。まずヨーロピアンコールオプションの関数をつくります。

def ecall(s,k,t,r,v):
    d1=(np.log(s/k)+(r+v**2/2)*t)/v/np.sqrt(t)
    d2=(np.log(s/k)+(r-v**2/2)*t)/v/np.sqrt(t)
    return s*norm.cdf(d1)-k*np.exp(-r*t)*norm.cdf(d2)

満期のペイオフ

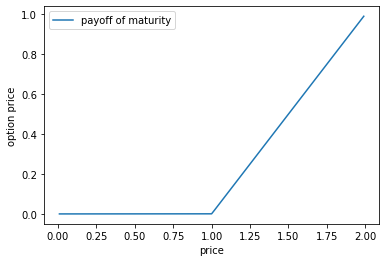
満期のペイオフができるかどうかを満期までの期間tを極力ゼロに近づけ、価格Sを0から2まで動かして確かめます。その他の変数は行使価格k=1,無リスク金利r=0,ボラティリティv=0.4と固定します。

c=[];s=[]
for i in range(1,200):
    s.append(i/100)
    c.append(ecall(s[i-1],1,0.00001,0,0.4))
plt.plot(s,c, label="payoff of maturity")
plt.xlabel('price')
plt.ylabel('option price')
plt.legend()
plt.show()

満期において行使価格を境にペイオフが４５度に折れ曲がるのが確認できます。これは満期時のペイオフそのものです。満期の時点での株価を$s_T$であらわすとmax($s_T-k,0$)と表現されることがあります。株価が行使価格よりも安ければ、オプションの買い手は行使価格で買う権利を放棄して市場で直接株式を購入することを示しています。この満期時のペイオフを本質的価値と呼びます。

残り２つの拘束条件

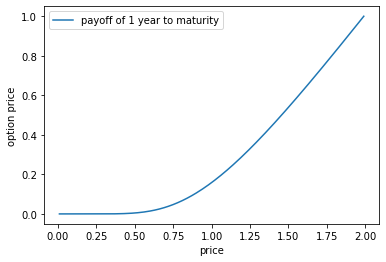
つぎに満期から１年前のオプション価格をチェックしてみましょう。t=1とします。

c=[]
for i in range(1,200):
    c.append(ecall(i/100,1,1,0,0.4))
plt.plot(c, label="payoff of 1 year to maturity")
plt.xlabel('price')
plt.ylabel('option price')
plt.legend()
plt.show()

一年前に株価がゼロのときはオプションの価値もゼロ、株価が2のときにはオプションの価値は1になることが確認できます。これは株価が行使価格が極端に離れているときのオプションの境界条件です。これはMMがヘッジをしたときに株価がゼロで、行使価格が1のときには行使される可能性がゼロであるので、ヘッジをする必要がないことを意味しています。つぎに、行使価格が1で株価が2であるときには満期に行使されるのが確実なために、100%の株式を保有していればヘッジになることを意味しています。どちらもMMにとってはヘッジの費用はゼロなので、オプションの価格は株価と行使価格の差の１になります。

時間的価値

s=[];c=[];c1=[];c2=[]
for i in range(1,200):
    s.append(i/100)
    c.append(ecall(s[i-1],1,1,0,0.4))
    c1.append(ecall(s[i-1],1,0.000001,0,0.4))
    c2.append(ecall(s[i-1],1,1,0,0.4)-ecall(s[i-1],1,0.000001,0,0.4))
plt.plot(s,c, label="payoff of 1 year to maturity")
plt.plot(s,c1, label="payoff at maturity")
plt.plot(s,c2, label="time value")
plt.xlabel('price')
plt.ylabel('option price')
plt.legend()
plt.show()

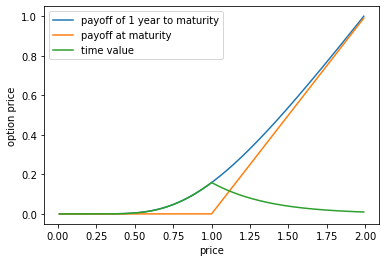
時間的価値はオプションの価値から本源的価値を引いたものです。時間的価値は他の条件が同じであれば時間の経過とともに減っていきます。青い線がオプションの価値、橙の線が本源的価値です。その差が時間的価値です。時間的価値は緑の線で表されています。行使価格を境に左右対称になっています。青い線は時間の経過とともに赤い線に近づいていきます。

コールの買いポジションの価値

コールのオプションには価値がありますが、コールを得るためにはその価値を対価として支払う必要があります。したがって、オプションペイオフの期待値を、同じ価値の現金で支払ったので、そのオプションを保有する正味の価値はゼロになります。そして、時間を固定して価格が動いた場合にどのような価値の動きになるかを見てみましょう。

s=[];c=[];c1=[];c2=[];c3=[]
c0=ecall(1,1,1,0,0.4)
for i in range(1,200):
    s.append(i/100)
    c.append(ecall(s[i-1],1,1,0,0.4)-c0)
    c1.append(ecall(s[i-1],1,0.000001,0,0.4))
    c2.append(ecall(s[i-1],1,0.5,0,0.4)-c0)
    c3.append(ecall(s[i-1],1,0.1,0,0.4)-c0)
plt.plot(s,c, label="value of 1 year to maturity")
plt.plot(s,c1, label="payoff at maturity")
plt.plot(s,c2, label="value at 0.5 year to maturity")
plt.plot(s,c3, label="value at 0.1 year to maturity")
plt.xlabel('price')
plt.ylabel('option price')
plt.legend()
plt.show()

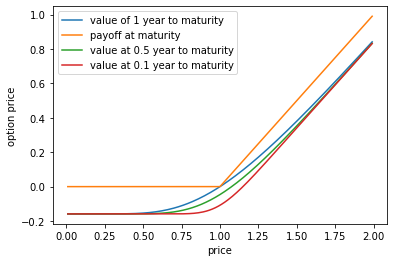
青い線は１年満期のポジションの価値です。時間を固定して価格を動かすと、価格が下落するとコールの価格分の損失が生じます。一方で、価格が上昇すると価値は上がりますがすでにオプションの価格を支払っているのでその分は差し引かれペイオフほどの利益は得られません。つぎに半年が経過したときを見てみましょう。それがグリーンの線です。価格が動かなくても時間的価値が減ってしまうので、その分ポジションの価値は減ります。価格が大きく下がる、または上がると青い線に近づいていきます。つぎに0.9年が経過したとしましょう。だいぶ満期に近づいています。その際にはさらに時間的価値が減ってしまいます。そしてポジションの価値の曲線はオプションのペイオフの折れ曲がった直線に近づいていきます。満期になると、ポジションの価値はペイオフを最初に支払ったオプションの価格分だけ平行移動した折れ曲がった直線になります。最初に払ったオプション価格を取り戻すには株価はすくなくとも行使価格からオプション価格分上昇している必要があります。

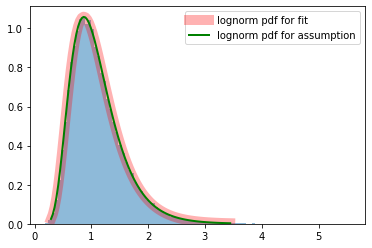
幾何ブラウン運動にしたがう確率変数の分布

　実際に生成した価格の時系列の分布をみてみましょう。幾何ブラウン運動にしたがう確率変数の確率密度関数は

$f(s,\mu,\sigma,t)=\frac{1}{\sqrt{2\pi}}\frac{1}{s\sigma\sqrt{t}}\exp (-\frac{([\ln(s)-\ln(S_0)-(\mu-0.5\sigma^2)t]^2}{2\sigma\sqrt{t}})$

となります。

def lognormal(x,mu,vol,t):
    tmp=1/np.sqrt(2*np.pi*t)/vol/x
    return tmp*np.exp(-(np.log(x)-(mu-0.5*vol**2)*t)**2/2/vol**2/t)

この関数を利用して

fig, ax = plt.subplots(1, 1)
ax.hist(S[:,nDays],bins=100,alpha=0.5,density=True)
s,l,sc = stats.lognorm.fit(S[:,nDays])
print('shape,loc,scale',s,l,sc)
x = np.linspace(lognorm.ppf(0.001, s),
                lognorm.ppf(0.999, s), 100)
ax.plot(x, lognorm.pdf(x, s,l,sc),
       'r-', lw=10, alpha=0.3, label='lognorm pdf for fit')
ax.plot(x, lognormal(x,mu,vol,1),
       'g-', lw=2, alpha=1, label='lognorm pdf for assumption')
plt.legend()
plt.show()

対数正規分布によりよく近似されるのが分かります。

オプション複製戦略

実際にオプションの複製に要する費用とペイオフの期待値がオプションプレミアムになるということをブラック―ショールズの方程式を解く過程で理解することは大変な困難をようすることから、複製戦略を構築して、実際の複製戦略の収益がオプションプレミアムと同等になることを見たほうが近道です。そこで、実際の複製戦略を構築してみましょう。

金利の取り扱い

　必要な資金全額を全額無リスク金利で借り入れで調達します。その資金で現物の株式を購入します。余った現金には無リスク金利が得られます。ブラック―ショールズ(BS)モデルでは金利は連続金利です。連続的な複利で利息を受け取り、再投資されます。実際にBSモデルを使う場合にはこの分を調整する必要があります。その際に新しいモデルを作る必要はなく、金利の調整で十分なことが研究報告されています。

オプションのデルタ

デルタはオプションの原資産の価格が１単位上昇したときにオプションの価格が上昇する割合を示しています。コールオプションのデルタは

$\Delta=\frac{\partial C}{\partial S}$
で表されます。

def option_replication(S,k,t,r,v):
    payoff=[]
    close=[]
    pl=[]
    interest=[]
    replication=[]
    rr=np.exp(r)-1
    for s in S:
        y=pd.DataFrame(s).copy()
        y.columns=['Close']
        y['pl']=0 #一日の損益を入れます。
        y['pos']=0 #デルタの保存
        y['pos_x_c']=0#取得費用
        y['cash']=0#現金残高
        y['int_income']=0#金利収入
        #init----------------------------------
        delta=norm.cdf((np.log(1/k)+(r+v**2/2)*t)/v/np.sqrt(t))
        y.iloc[0,2]=delta
        y.iloc[0,3]=delta*1
        y.iloc[0,4]=(1-delta)#現金
        y.iloc[0,5]=y.iloc[1].cash*r/250
        delta0=delta
        dpl0=0
        for i in range(1,len(y)):
            tt=t-i/250
            c=y.Close.iloc[i] #その日の価格の取得
            c0=y.Close.iloc[i-1] #前日の価格の取得
            delta=norm.cdf((np.log(c/k)+(r+v**2/2)*tt)/v/np.sqrt(tt))
            y.iloc[i,2]=delta# デルタ
            y.iloc[i,3]=y.iloc[i-1,3]+(delta-delta0)*c# 在庫保有費用
            dpl=delta*c-y.iloc[i,3]# 損益の計算
            y.iloc[i,1]=dpl #売買損益
            y.iloc[i,4]=-(delta-delta0)*c+y.int_income.iloc[i-1] #現金
            y.iloc[i,5]=sum(y.cash.iloc[:i-1])*rr/250#金利収入の計算
            delta0=delta
            dpl0=dpl
        payoff.append(max(c-k,0))
        close.append(c)
        pl.append(y.iloc[-1:,1])
        interest.append(sum(y.iloc[:,5]))
        replication.append(y.pl.iloc[-1:]+sum(y.int_income)-r)
    return np.array(payoff),np.array(close),np.array(pl),np.array(interest),np.array(replication)

実際に実行してみます。

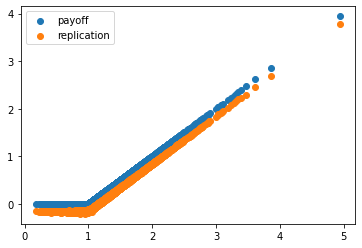
payoff,close,pl,interest,replication=option_replication(S,1,1,0.1,0.4)

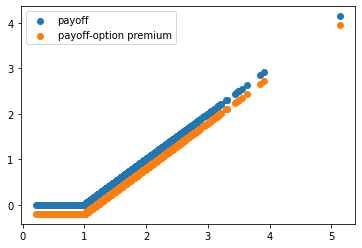
payoffはそれぞれの１年のシミュレーション結果の満期時点のペイオフ、closeは終値、plは複製トレーディング戦略の損益、interestは複製戦略の現金ポジションの金利収入です。まず、理論価格を見てみます。closeをｘ軸として散布図を描いて、特徴を捕えます。

plt.scatter(close,payoff,label='payoff')
plt.scatter(close,payoff-ecall(1,1,1,0.1,0.4),label='payoff-option premium')
plt.legend()
plt.show()
np.mean(payoff),ecall(1,1,1,0.1,0.4)
# (0.22784013626824448, 0.203184693100587)

ペイオフの平均は0.228にたいして、オプションの理論価格は0.203です。オプションの購入を借り入れで行ったとすると、その費用は0.203x0.1=0.0203です。したがって、最終的な損益は0.228-0.203-0.02=0.005です。ほぼゼロになり借り入れで収益を得ることができないことが分かります。リスク中立な世界です。

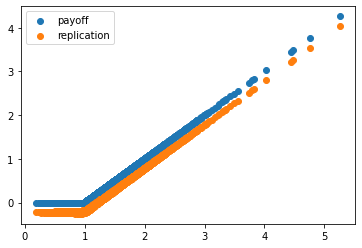
つぎにオプションの複製戦略について見ていきます。

plt.scatter(close,payoff,label='payoff')
plt.scatter(close,replication,label='replication')
plt.legend()
plt.show()
np.mean(replication)

# 0.002646229899742185

ヘッジ比率の調整

複製戦略について順を追って考えていきましょう。$S_0$をコールオプション取引成立の時点の株価とします。MMはコールオプションの想定元本分の現金を借り入れにより用意します。この場合は1です。この取引と同時にデルタ($S_0$)分の株式($D_0$)を購入します。現金は$D_0 \cdot S_0$分減ります。現金には無リスク金利がつきます。
借入資金1
株式数:$D_0$
株価購入:$D_0\cdot S_0$
現金:$1-D_0\cdot S_0$
資産の総価値:$D_0\cdot S_0+1-D_0\cdot S_0$

Ⅰ期間後に株価が上昇したとしましょう。$S_1>S_0$です。

現金の金利収入:$(1-D_0\cdot S_0)\cdot r/250$
資産の総価値:$D_0\cdot S_0+(1-D_0\cdot S_0)\cdot (1+r/250)$

デルタ($D_1$)は増えます。$D_1-D_0$分の株式を買い増す必要が生じます。現金はデルタ調整$(D_1-D_0)\cdot S_1$分減ります。

株式数:$D_0$
株価購入:$D_0\cdot S_0+(D_1-D_0)\cdot S_1$
現金:$(1-D_0\cdot S_0)\cdot (1+r)/250-(D_1-D_0)\cdot S_1$
資産の総価値:$D_1\cdot c-(D_0\cdot S_0+(D_1-D_0)\cdot S_1)+(1-D_0\cdot S_0)\cdot (1+r/250)-(D_1-D_0)\cdot S_1$

このまま満期まで株価が上がり続ければ、資産は増え続けます。しかし、すこしづつ株式を買い増しているので、最初から全額株式に投資ていた時ほどには資産は増えません。

２期間後に株価は下落し、$S_2=S_1$に戻ってしまったとしましょう。デルタは減少します。$D_2<D_1$ですからデルタの減少分だけ株式を売却する必要があります。この場合、高値で買った株式を安値で売ることになるので、損失が生じます。コールオプションの買いポジションの複製では、株価が上下動すると損失がはっせいします。この損失は複製費用と呼ばれオプションプレミアムの一部を構成します。

複製戦略の総収益は株価の上下動による損益とデルタによる在庫調整による実現損益と現金在庫の金利収入になります。株式保有・調整による損益はplに保存され、現金在庫からの無リスク金利収入はinterestに保存されています。また、この戦略には借入費用がかかります。最終的な損益は 0.0026となり、ほとんど利益は得ません。複製戦略から計算したオプションプレミアムは(0.2278-0.0026)/1.1=0.2047とBSモデルのものとほぼ同じになりました。

つぎは金利をゼロとしたシミュレーションです。

# (満期のペイオフ：0.15631763295633652, BSモデルの価格：0.15851941887820603)

# -0.0018947039197326307

BSモデルによる価格(0.1585)とペイオフ(0.1563)、複製戦略の正味の利益は-0.019で、借り入れからは利益が得られないのが分かります。複製戦略のオプションプレミアムは0.156-(-0.019)=0.1582でBSモデルとの差は(0.003)となります。

リスク中立な世界での結果のまとめ

金利１０％(期待ペイオフ=0.228)

-コールオプションの買い
    - コールオプション価格=0.203
    - コールオプション買い入れ資金の金利=0.203x0.1=0.0203
    - 正味の収益=0.228-0.203-0.0203=0.0047
- コールオプションの買いの複製
    - オプション複製に必要な資金の借入=1
    - オプション複製に必要な資金の借入費用=0.1
    - オプション複製による損益=0.1026
    -正味の利益= 0.1026-0.1=0.0026  
        -複製によるコールオプション価格=(0.228-0.0026)/1.1=0.2049

金利0%(期待ペイオフ=0.1563)

-コールオプションの買い
    - コールオプション価格=0.1585
    - コールオプション買い入れ資金の金利=0.1585x0=0
    - 正味の収益=0.1563-0.1585-0=-0.0022
- コールオプションの買いの複製
    - オプション複製に必要な資金の借入=1
    - オプション複製に必要な資金の借入費用=0
    - オプション複製による損益=-0.0019
    - 正味の利益=-0.0019  
        -複製によるコールオプション価格=(0.1563-(-0.0019))/1=0.1582

10%と0%という２つの無リスク金利の状況において、ブラックショールズモデルのオプション価格とブラックショールモデルのデルタを用いた複製戦略から算出されたオプション価格がほぼ同じになることを確認できました。また、リスク中立確率のもとでは借り入れによる投資戦略からはリターンが得られないことも分かりました。コールオプションを購入して株式投資しても、オプション複製戦略を用いて投資をしても借り入れで得られた資金を元手に投資をしても、たまたか大きな利益を得られることがあるかもしれませんが、同じ戦略をなんども繰り返すことで、正味のリターンはゼロに収束していきます。

正確ではないにしてもオプションのプレミアムがヘッジの費用とペイオフの期待収益から成り立っていることを理解いただけたのではないかと思います。

現実世界はリスク中立な世界とは違う

リスク中立な世界を考えてオプションの価格を決める方法は理解できたように思います。しかし、現実世界はそうではないので、その場合にどうなるかをシミュレーションで試してみようと思います。実際の株価は10％上昇するとします。そして、そのときの無リスク金利はゼロとします。オプションの価格は実際の株価の収益率に影響はうけずに無リスク金利に影響を受けるので、それがそのまま成り立っているとすると、コールオプションは安く買えてしまえます。その際の価格は0.1563でした。さて、株価の期待値が10%のときに、無リスク金利を0%としてデルタを計算して、コールオプションを複製したらその結果がどうなるかを調べてみましょう。

payoff,close,pl,interest,replication=option_replication(S,1,1,0,0.4)

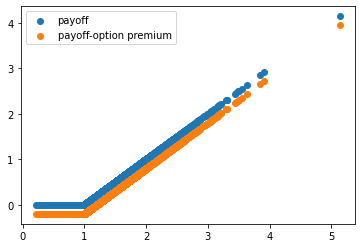
Sは株価の期待値を10%として生成したデータです。それを無リスク金利を0%としてコールオプションの買いポジションを複製しました。結果はペイオフの期待値は0.23163357710645846、コールオプションの理論価格は 0.15851941887820603です。したがって、コールオプションを安く手に入れることができる一方で、株価の期待値は高いので、その差がこの戦略の収益になります。それは0.0731です。コールオプションの複製の結果もほぼ同じです。

plt.scatter(close,payoff,label='payoff')
plt.scatter(close,replication,label='replication')
plt.legend()
plt.show()
np.mean(replication)

# 0.073407911540944

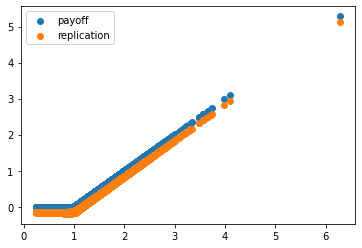
それは0.0734です。これはコールを買う人にとってはいいのですが、売る人にとってはどうなるのでしょうか？売る人にとってのコールオプションの価格は0.1585です。一方で株価の期待ペイオフは-0.2316です。したがって、コールオプションを売った人は0.2316の損失になります。コールオプションを売った時に受け取るプレミアムは0.1585ですから、正味の収益は-0.2316+0.1585=-0.0731です。当たり前ですが、コールオプションを買った人のちょうど逆になります。これをオプションの複製でも試してみましょう。

def option_replication2(S,k,t,r,v):
    payoff=[]
    close=[]
    pl=[]
    interest=[]
    replication=[]
    rr=np.exp(r)-1
    for s in S:
        y=pd.DataFrame(s).copy()
        y.columns=['Close']
        y['pl']=0 #一日の損益を入れます。
        y['pos']=0 #デルタの保存
        y['pos_x_c']=0#取得費用
        y['cash']=0#現金残高
        y['int_income']=0#金利収入
        #init----------------------------------
        delta=-norm.cdf((np.log(1/k)+(r+v**2/2)*t)/v/np.sqrt(t))
        y.iloc[0,2]=delta
        y.iloc[0,3]=delta*1
        y.iloc[0,4]=(1-delta)#現金
        y.iloc[0,5]=y.iloc[1].cash*r/250
        delta0=delta
        dpl0=0
        for i in range(1,len(y)):
            tt=t-i/250
            c=y.Close.iloc[i] #その日の価格の取得
            c0=y.Close.iloc[i-1] #前日の価格の取得
            delta=-norm.cdf((np.log(c/k)+(r+v**2/2)*tt)/v/np.sqrt(tt))
            y.iloc[i,2]=delta# デルタ
            y.iloc[i,3]=y.iloc[i-1,3]+(delta-delta0)*c# 在庫保有費用
            dpl=delta*c-y.iloc[i,3]# 損益の計算
            y.iloc[i,1]=dpl #売買損益
            y.iloc[i,4]=-(delta-delta0)*c+y.int_income.iloc[i-1] #現金
            y.iloc[i,5]=sum(y.cash.iloc[:i-1])*rr/250#金利収入の計算
            delta0=delta
            dpl0=dpl
        payoff.append(min(-c+k,0))
        close.append(c)
        pl.append(y.iloc[-1:,1])
        interest.append(sum(y.iloc[:,5]))
        replication.append(y.pl.iloc[-1:]-sum(y.int_income)+r)
    return np.array(payoff),np.array(close),np.array(pl),np.array(interest),np.array(replication)

デルタにマイナスが付いている以外はほぼすべて最初のものと同じです。そうするとその結果は

payoff,close,pl,interest,replication=option_replication2(S,1,1,0,0.4)

plt.scatter(close,payoff,label='payoff')
plt.scatter(close,replication,label='replication')
plt.legend()
plt.show()
np.mean(replication)

#-0.0734079115409449

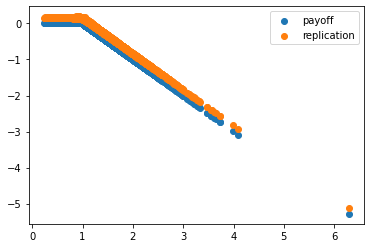
損失は期待通りの-0.0734です。これでは買い手に有利、売り手に不利になります。これではMMの行動に大きな影響がありそうですが、MMも売りと買いのバランスのよいポートフォリオをもてば買いポジションの収益で売りポジションの損益を補えます。しかし、バランスの良いポートフォリをもつのは難しいために、問題の解決策が必要です。

マーケットメイカが矛盾の調節をしている

この問題は結局オプションのプレミアムに反映されます。そうするとどこかでそのプレミアムの上昇を調整しなければなりませんが、それをボラティリティで調整します。これをインプライドボラティリティといいます。これはオプションプレミアムからBSMモデルを通して逆算するボラティリティのことです。しかし、この解決策はギルサノフの定理と呼ばれるリスク選好の方法を変えてもボラティリティは変わらないとする考え方と矛盾します？

この問題は株価の自己回帰モデルとしても扱われます。Lo and Wang(1995)

参考

CAPM

ファイナンシャルエンジニアリング by John Hull 28.1によると株式が十分に取引されていれば

$\lambda=\frac{\mu-r}{\sigma}$
が成り立つので、オプションの価格は適切なボラティリティで算出されるとされています。

リスクプレミアムを考慮に入れて、割引率を調整する

ファイナンシャルエンジニアリング by John Hull 35.1によると、別の方法としては株価の期待収益率が無リスク金利よりも高いことの調整は、リスクプレミアムを載せた割引率で調整するというのがあります。結果はリスク中立世界のオプション価格と同じになります。この方法ではMMの抱える問題の解決策とはなりません。

原資産である株式の価格が幾何ブラウン運動にしたがう

最初のグラフで一番株価が上昇したグラフも、一番下落したグラフも観測される可能性があります。その際に、観測値がそれだけだというケースは十分にあり得ます。そのような特性を持つ株価について適切にモデル化をすることは可能なのでしょうか？それぞれの観測値のデータ点は２５０個です。予測する個数としては十分な気がしますが、これで期待値10％、ボラティリティ40％を予測することができるでしょうか？

参考

Black–Scholes equation
Black–Scholes model
Itô's lemma
フィナンシャルエンジニアリング　by　ジョンハル
入門 計量経済学 by ストック,ワトソン
Econometrics by Fumio Hayashi
Basic Econometrics by Gjarati

Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。