モンテカルロ法は、乱数を用いてシミュレーションや数値計算を行う手法で、金融の分野においても注目されています。ある金融資産の価値は、正味現在価値法により算出可能ですが、様々なシナリオが将来に想定される場合には計算は困難を極めます。そのような場合に、モンテカルロ法は有効な手段です。
金融の世界では、金融資産の価値の評価、リスク管理、トレーディング戦略の収益性の確認などにモンテカルロ法が活用されています。そこでは、価格の動きを幾何ブラウン運動として表現することがしばばしばです。アメリカンオプションの評価、リスク管理に用いられるモンテカルロ法はこの例です。そこでまず幾何ブラウン運動を再現し、その問題点を探ってみたいとおもいます。その動きは
$\mathrm{d}S_t=\mu S_t \mathrm{d}t+\sigma \sqrt{\mathrm{d}t} S_t\mathrm{d}W_t$ (1)
の確率微分方程式(SDE)を解くことで得られます。$S_t$は$t$時点の株価です。$\sigma$は価格変動の程度を、$\mu$は株価のトレンドをあらわす定数です。$W_t$は標準ウィナー過程です。$\mathrm{d}W_t$は標準正規分布にしたがいます。
$\mu$も$\sigma$も株価がもつ特有の特性で、過去の価格データから推定されます。このSDEを解くと
$S_{t}=S_{t-1}\exp[(\mu-0.5\sigma^2)\mathrm{d}t+\sigma \sqrt{\mathrm{d}t} \mathrm{d} W_t]$ (1)`
が得られます。
$S_t$の幾何ブラウン運動は
期待値 $\exp(\mu t)S_0$、
分散 $\exp(2\mu t)S_0^2(\exp(\sigma^2t)-1)$
で連続的に動く確率過程です。これは$S_{t}=S_{0}\exp[(\mu-0.5\sigma^2)t+\sigma \sqrt{t} W_t]$とすれば見通しが良くなります。
また、対数価格の差$\ln S_t-\ln S_0$は
期待値 $(\mu - 1/2 \sigma^2) t$、
分散 $\sigma^2t$
となります。
モンテカルロシミュレーションを用いて、時系列データを作ってみましょう。genSという関数で株価を再現します。コードの重要な部分は、
w=rng.standard_normal( size=(1,nDays)).T
です。ここで乱数を発生しています。これは(1)式の$\mathrm{d}W_t$に相当します。また、
x = np.exp((mu - 0.5*sigma ** 2) * dt + w*np.sqrt(dt)*sigma)
は(1)'式そのものです。
import numpy as np
from numpy.random import default_rng, Generator, PCG64, MT19937
import matplotlib.pyplot as plt
from scipy.stats import norm, lognorm
from scipy import stats
from datetime import datetime, date,time
import pandas as pd
DAYS=240
def genS(mu,sigma0,nDays,nSim):
#np.random.seed(1)
sigma = np.array([sigma0])
dt = 1/DAYS
S = np.array([[0.0 for i in range(nDays+1)] for j in range(nSim)])
for j in range(nSim):
rng = np.random.default_rng()
w=rng.standard_normal( size=(1,nDays)).T
x = np.exp((mu - 0.5*sigma ** 2) * dt + w*np.sqrt(dt)*sigma)
x = np.vstack([np.ones(len(sigma)), x])
x = x.cumprod(axis=0)
S[j][:]=x.ravel()
return S
t1=datetime.now()
vol=0.4 #0.65
mu=0.1#0.004
nDays=DAYS*5
S=genS(mu,vol,nDays,1000000)
print(datetime.now()-t1)
# 0:02:58.916157
5年後の株価の動きはつぎの分布として与えられます。
fig, ax = plt.subplots(1, 1)
ax.hist(S[:,nDays],bins=100,density=True)
plt.show()

右にすそ野の長い分布が見て取れます。実際に生成した価格の時系列の分布を幾何ブラウン運動にしたがう確率変数の確率密度関数として見てみましょう。
$f(s,\mu,\sigma,t)=\frac{1}{\sqrt{2\pi}}\frac{1}{s\sigma\sqrt{t}}\exp (-\frac{([\ln(s)-\ln(S_0)-(\mu-0.5\sigma^2)t]^2}{2\sigma^2t})$
def lognormal(x,mu,vol,t):
tmp=1/np.sqrt(2*np.pi*t)/vol/x
return tmp*np.exp(-(np.log(x)-(mu-0.5*vol**2)*t)**2/2/vol**2/t)
となります。この関数を利用してヒストグラムに当てはめてみます。また、stats.lognorm.fitを用いて当てはまりの具合を確認します。
s,l,sc = stats.lognorm.fit(S[:,nDays])
print('shape,loc,scale',s,l,sc)
fig, ax = plt.subplots(1, 1)
x = np.linspace(lognorm.ppf((1/nSim), s),
lognorm.ppf((1-1/nSim), s), 100)
ax.hist(S[:,nDays],bins=x,alpha=0.9,density=True,label='frequency')
ax.plot(x, lognorm.pdf(x, s,l,sc),
'r-', lw=10, alpha=0.3, label='lognorm pdf fit')
ax.plot(x, lognormal(x,mu,vol,nDays/DAYS),
'g-', lw=2, alpha=1, label='lognorm (GBM)')
plt.legend()
plt.show()
stats.probplot(S[:,nDays], dist="lognorm", sparams=(s,l,sc),plot=plt)
plt.show()
# shape,loc,scale 0.894475419474593 -0.00037471616307207243 1.1066290128309144
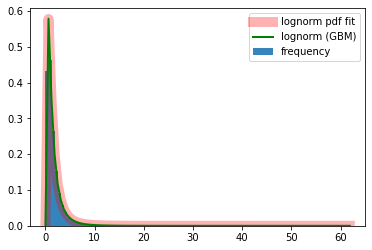
かなり当てはまりがよいように思えます。分布の胴体部分の当てはまりは、見た感じで確認できるのですが、テイル部分の当てはまりが確認できません。そこでp-pプロットを用いて確認します。直線が理論値で、ドットが観測値です。y軸はFillibenの推定値です。
stats.probplot(S[:,nDays], dist="lognorm", sparams=(s,l,sc),plot=plt)
plt.show()
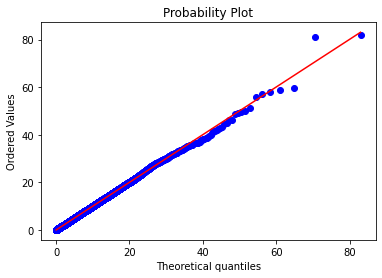
上側のテイルの部分で理論値との乖離が見られます。また、価格の理論分布の上限が60強であることに比べ、モンテカルロ法で生成された価格の最大値は80を超えてしまいます。これが幾何ブラウン運動にみられる心配事です。幾何ブラウン運動で株価を再現することは現実的なのか、モンテカルロ法では過大な上昇が起こりやすいのではないかという点です。
$f(s,\mu,\sigma,t)=\frac{1}{\sqrt{2\pi}}\frac{1}{s\sigma\sqrt{t}}\exp (-\frac{([\ln(s)-\ln(S_0)-(\mu-0.5\sigma^2)t]^2}{2\sigma^2t})$
の分布ですが、これは平均 $(\mu-0.5\sigma^2)t$、分散 $\sigma^2 t$の価格の対数が正規分布にしたがうのと同等です。確かめてみましょう。
stats.norm.pdf(0,(mu-0.5*vol**2),vol),lognormal(1,mu,vol,1)
# (0.9961097852369101, 0.9961097852369101)
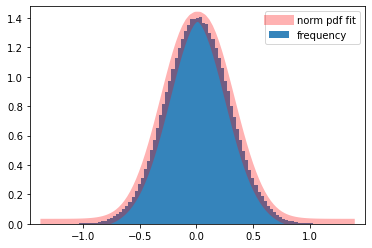
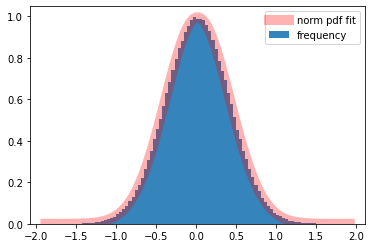
この関数を利用してヒストグラムに当てはめてみます。また、stats.norm.fitを用いて当てはまりの具合を確認します。価格を対数正規分布で分析するよりも、対数価格を正規分布で分析した方が、価格の上昇、下落が対称になり、見た感じで理解しやすくなります。
def MCsim(S,nDays,nSim):
s,l = stats.norm.fit(np.log(S[:,nDays]))
print('shape,loc',s,l)
fig, ax = plt.subplots(1, 1)
x = np.linspace(norm.ppf(1/nSim,(mu-0.5*vol**2)*nDays/DAYS,vol*np.sqrt(nDays/DAYS)),
norm.ppf(1-1/nSim,(mu-0.5*vol**2)*nDays/DAYS,vol*np.sqrt(nDays/DAYS)), 100)
ax.hist(np.log(S[:,nDays]),bins=x,alpha=0.9,density=True,label='frequency')
ax.plot(x, norm.pdf(x, s,l),
'r-', lw=10, alpha=0.3, label='norm pdf fit')
#ax.plot(x, lognormal(x,mu,vol,nDays/DAYS),
# 'g-', lw=2, alpha=1, label='lognorm (GBM)')
plt.legend()
plt.show()
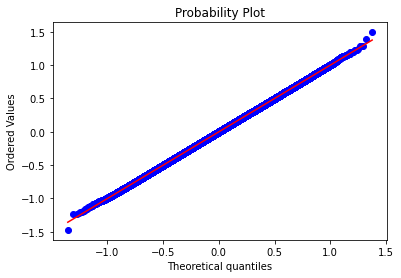
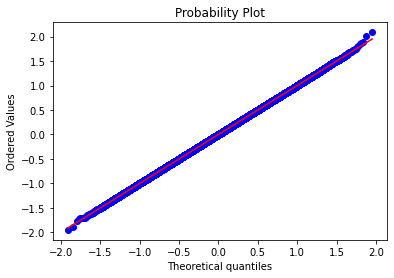
stats.probplot(np.log(S[:,nDays]), dist="norm", sparams=((mu-0.5*vol**2)*nDays/DAYS,vol*np.sqrt(nDays/DAYS)),plot=plt)
plt.show()
MCsim(S,nDays,nSim)
# shape,loc 0.10081979720534623 0.8949253884395363
上昇側のテイルの部分が直線から乖離しているのが分かります。
期間を短くして、120、240日で見てみましょう。
MCsim(S,120,nSim)
MCsim(S,240,nSim)
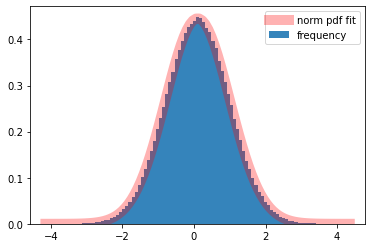
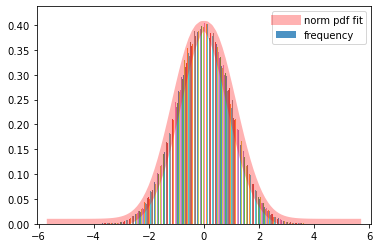
影響は残っています。そこで正規乱数の精度について調べてみましょう。正規乱数の生成ではnSim=100000にしています。probplotがメモリーを必要とするために小さくしてあります。
t1=datetime.now()
nDays=240*5
rng = Generator( PCG64())
nSim=100000
w = np.array([[0.0 for i in range(nDays)] for j in range(nSim)])
for j in range(nSim):
x=rng.standard_normal( size=(1,nDays)).T
w[j][:]=x.ravel()
s,l = stats.norm.fit(w)
x = np.linspace(norm.ppf(2/nDays/nSim, s),
norm.ppf(1-2/nDays/nSim, s), 100)
fig, ax = plt.subplots(1, 1)
ax.hist(w,bins=x,alpha=0.8,density=True,label='frequency')
print('shape,loc,scale',s,l)
ax.plot(x, norm.pdf(x, s,l),
'r-', lw=10, alpha=0.3, label='norm pdf fit')
plt.legend()
plt.show()
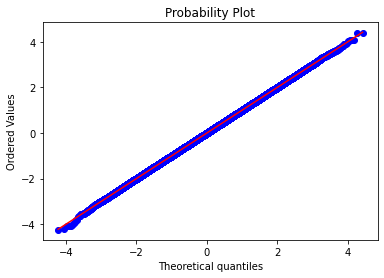
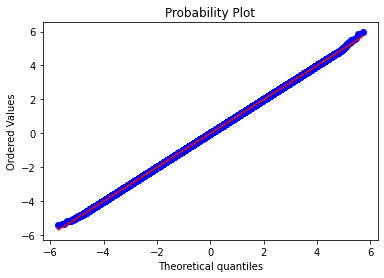
stats.probplot(w.ravel(), dist="norm",plot=plt)
plt.show()
print(datetime.now()-t1)
テイルの部分にわずかに乖離があるのが分かります。こちらは乱数の生成の数が1000002405なので、実際にグラフにしてみている確率変数の数は5年、1年、半年の1000000に比べて圧倒的に多いです。それでもテイルの部分に理論値からの乖離があるのは何らかの方法で改善した方がいいのかもしれません。
今回は乱数のジェネレーターとしてPCG64を使っていますが、
from numpy.random import default_rng
from numpy.random import Generator, PCG64, MT19937
を使うことでさまざまな検証がPythonできるようになっています。メルセンヌツイスター(MT19937)を使って試してみるのもいいかと思います。
Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。