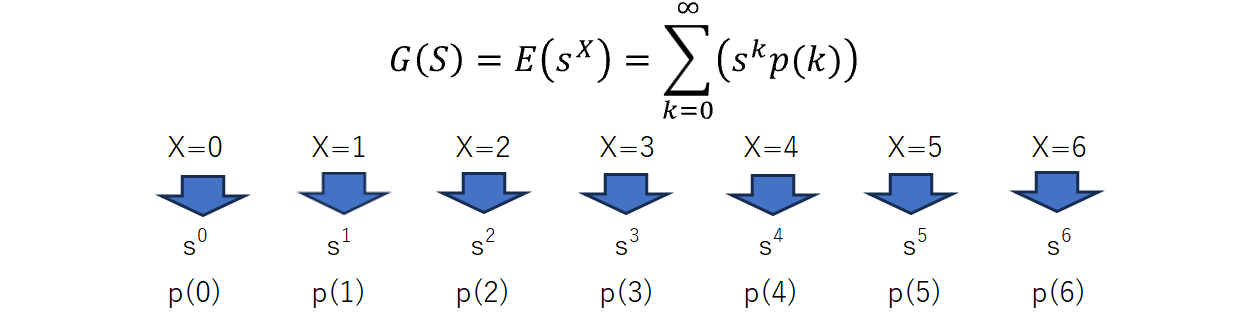母関数入門
数学史において、数列や級数の性質を調べることは重要なテーマの一つでした。これらの性質を理解し、表現するために様々な方法が開発されてきました。その中でも、漸化式と母関数は特に強力なツールです。フィボナッチ数列とド・モアブルの業績は、これらの概念を理解するのに最適な例です。
母関数とは、数列や確率分布を関数という入れ物に入れ、四則演算等の代数操作で漸化式や和の組み合わせの総和(畳み込み)を処理して、その係数(または微分)から個数・確率・モーメントを一括して取り出す“装置”です。
「母」は“生成する(親になる)”の意で、英語では generating function/独語では erzeugende Funktion の訳で、生成関数の同義語です。物理では「生成汎関数」も同系です。ゆえに「母関数」は目的別“生成装置”の総称です。
- 普通母関数(OGF):$A(x)=\sum a_n x^n$ は係数列 $a_n$ を生成(係数抽出で回収)。
- 指数型母関数(EGF):$E(x)=\sum a_n \dfrac{x^n}{n!}$ は$n$依存の列を微分方程式的に生成。
- 確率母関数(pgf):$G(s)=E[s^X]$ は確率 $P(X=k)$ を生成(係数が確率)。
- 積率母関数(mgf):$M(t)=E[e^{tX}]$ はモーメント $E[X^m]$ を生成($m$階微分の $t=0$ 評価)。
- 累積母関数:$K(t)=\log M(t)$ はクムラントを生成。
- 行列OGF:$G(z)=\sum z^n T^n=(I-zT)^{-1}$ は反復 $T^n$を生成(マルコフ/線形系)。
- 物理の分配関数/生成汎関数:$Z$・$Z[J]$ は平均・相関を生成(微分・変分で抽出)。
フィボナッチ数列と母関数
簡単な漸化式 $F_n = F_{n-1} + F_{n-2}$ で定義されたフィボナッチ数列から派生する性質は複雑であり、数学の多くの分野で応用が見られます。特に、この数列の成長率が黄金比 $\phi = \frac{1 + \sqrt{5}}{2}$ に収束することは、数学の美しい結果の一つです。
漸化式 $F_n=F_{n-1}+F_{n-2}$ に $F_n=r^n$ を代入します。
$$
r^n=r^{n-1}+r^{,n-2}
$$
両辺を $r^{n-2}$で割ると常に
$$
r^2=r+1 \quad(\ast)
$$
になります。
$(\ast)$ の解は
$$
r=\phi=\frac{1+\sqrt5}{2},\qquad r=\hat\phi=\frac{1-\sqrt5}{2}.
$$
となります。この2次方程式は「最初から解く対象」ではなく、等比形 $F_n=r^n$ を漸化式に代入して帰結する特性方程式を、ふつうの解の公式で解いているだけです。
$ax^2+bx+c=0$の係数を$a=1,\ b=-1,\ c=-1$として、解の公式より
$$
r=\frac{-b\pm\sqrt{b^2-4ac}}{2a}
=\frac{1\pm\sqrt{1+4}}{2}
=\frac{1\pm\sqrt{5}}{2}.
$$
-
よって根は $\phi=\dfrac{1+\sqrt5}{2}$ と $\hat\phi=\dfrac{1-\sqrt5}{2}$。
-
$r^2-r-1=0$ の2根は $\frac{1\pm\sqrt5}{2}.$
そのうち 大きい方を慣習的に $\phi=\frac{1+\sqrt5}{2}$(黄金比)、小さい方を $\hat\phi=\frac{1-\sqrt5}{2}$ と呼びます。
この解は「シフト=$x$倍」と関連します。
漸化式 $F_n=F_{n-1}+F_{n-2}\ (n\ge2)$ に両辺 $x^n$ を掛けて $n\ge2$ で和をとると
$$
\sum_{n\ge2}F_nx^n=\sum_{n\ge2}F_{n-1}x^n+\sum_{n\ge2}F_{n-2}x^n.
$$
となり、これらのシフト写像は
$\sum_{n\ge2}F_{n-1}x^n=x\sum_{m\ge1}F_mx^m=x\bigl(G(x)-F_0\bigr)=xG(x)$、
$\sum_{n\ge2}F_{n-2}x^n=x^2\sum_{m\ge0}F_mx^m=x^2G(x)$、
$\sum_{n\ge2}F_nx^n=G(x)-F_0-F_1x=G(x)-x$。
です。よって、
$$
\bigl(G(x)-x\bigr)=xG(x)+x^2G(x)\ \Rightarrow
(1-x-x^2),G(x)=x,
$$
となり
$$
G(x)=\frac{x}{1-x-x^2}.
$$
が得られます。ここで出てきた $G(x) = \frac{x}{1 - x - x^2}$ を分析することでいろいろな性質が分かり、フィボナッチ数列の母関数とよばれます。
線形結合が一般解
$r^2-r-1=0$という2 次方程式(特性方程式)を解いて得られる $r=\phi,\ \hat\phi$ に対し、$F_n=\phi^n$ と $F_n=\hat\phi^n$ はどちらも解となり、線形性より
$$
F_n=A\phi^n+B\hat\phi^{,n}
$$
が一般解となります。初期条件で $A,B$ が決まります。
なぜ分母の零点を見るのか
-
漸化式から $G(x)=\frac{x}{1-x-x^2}$ が出ます。
-
分母を因数分解すると
$$
1-x-x^2=(1-\phi x)(1-\hat\phi x)
$$
($\phi+\hat\phi=1,\ \phi\hat\phi=-1$ より成立)
となり、 $x=\tfrac{1}{\phi},\tfrac{1}{\hat\phi}$ が $G(x)$ の極(特異点)です。
よって
$$
\frac{x}{(1-\phi x)(1-\hat\phi x)}
=\frac{A}{1-\phi x}+\frac{B}{1-\hat\phi x}.
$$
両辺に分母を掛けて
$$
x=A(1-\hat\phi x)+B(1-\phi x)=(A+B)-x(A\hat\phi+B\phi).
$$
係数比較で
$$
A+B=0,\qquad 1=-(A\hat\phi+B\phi)=A(\phi-\hat\phi)=A\sqrt5,
$$
したがって
$$
A=\frac{1}{\sqrt5},\quad B=-\frac{1}{\sqrt5}.
$$
- 等比級数展開
$\ |x|<\min{1/|\phi|,1/|\hat\phi|}=1/\phi\ $で
$$
\frac{1}{1-\phi x}=\sum_{n\ge0}(\phi x)^n,\qquad
\frac{1}{1-\hat\phi x}=\sum_{n\ge0}(\hat\phi x)^n.
$$
したがって
$$
G(x)=\frac{1}{\sqrt5}\sum_{n\ge0}\bigl(\phi^n-\hat\phi^n\bigr)x^n.
$$
- 係数抽出(=一般項)
$$
[x^n]G(x)=\frac{\phi^n-\hat\phi^n}{\sqrt5}=F_n.
$$
(なぜ“極が一次”だと良いか)
$G(x)$ の分母が $(1-\phi x)(1-\hat\phi x)$ と一次因子の積なので、部分分数が
$$
\frac{A}{1-\phi x}+\frac{B}{1-\hat\phi x}
$$
と一次の極(単純極)に分かれ、各項が等比級数に直ちに展開できます。結果として、係数は指数型の線形結合($A\phi^n+B\hat\phi^n$)になり、初期条件で定数が決まります。
$A=\tfrac{1}{\sqrt5},\ B=-\tfrac{1}{\sqrt5}$、すなわち
$$
F_n=\frac{\phi^n-\hat\phi^{,n}}{\sqrt5}.
$$
- 分母の零点=生成関数の極が、冪級数の係数に指数型 $r^n$を生みます。
- $1-x/r$ の形に分解できれば、$1/(1-x/r)=\sum_{n\ge0}(x/r)^n$ の係数は $r^{-n}$。よって係数は $r^n$ 型の線形結合になります(定数は初期条件で決定)。
数列と確率変数
漸化式がすでに自明な情報を使って、次の数列を作ったのに対して、確率過程は次に何が来るかわからないので、外部から与えられると考えます。素な確率変数の列(ベルヌーイ過程)${X_n}$ を独立同分布、$X_n\sim\mathrm{Bernoulli}(p)$ とします。ここでは次の値は既知情報からは決まらず、外部から到来する独立な入力(ノイズ/イノベーション)、外生変数として与えられます。ベルヌーイ列$X_{n+1}$ は過去から独立に分布 $P(X=1)=p$ で与えられます。
単に並べただけのベルヌーイ過程は
$$
X_n\in{0,1},\ P(X_n=1)=p
$$
と記述できます。一般解としては、独立な一様乱数 $U_n\sim\mathrm{Unif}(0,1)$ を用意し
$$
X_n=\mathbf{1}{U_n\le p}
\quad\text{(同値に)}\quad
X_n=F^{-1}(U_n),
$$
と書けます。ただし $F^{-1}$はベルヌーイの分布関数 $F(x)$ に対する分位点関数です。
この母関数は
$$
G_{X_n}(s)=E[s^{X_n}]=(1-p)+ps\qquad(\forall n).
$$
で与えられます。確率母関数 $G_{X_n}(s)=(1-p)+ps$ は「$X_n$ の分布($P(X_n=0)=1-p,\ P(X_n=1)=p$)」を符号化したもので、決定論の“一般項”のような $X_n$ の値そのものは与えません。アブラハム・ド・モアブルは、母関数を単にサンプリング理論を作るために整備したというよりは、漸化式と融合することで、より汎用的な分析手法として使えるようにしました。それが20世紀に爆発したということです。
ド・モアブルの業績
アブラハム・ド・モアブルは成功確率 $p$ の独立試行を $n$ 回行ったときの成功回数の確率過程について調べ、そして成功回数の分布が、$n$ が十分大きい場合に正規分布に近似されることを示しました。これらは冪級数の展開と極限の概念を通じて数学的に理解され、統計学におけるサンプリング理論の基礎を形成しました。この帰結に至る過程で、複雑な計算過程を体系化するために母関数は大きな役割を果たしました。
2項過程(ベルヌーイ反復)の $n=3$ で、母関数と数え上げを並べます。
設定
$X_i\sim\mathrm{Bernoulli}(p)$ 独立、$S_3=X_1+X_2+X_3$、$q=1-p$。
母関数(pgf)
1 回の pgf は $G_X(s)=q+ps$。独立和で
$$
G_{S_3}(s)=(q+ps)^3
= q^3 + 3q^2ps + 3qp^2s^2 + p^3 s^3.
$$
よって
$$
P(S_3=0)=q^3,\ \ P(S_3=1)=3q^2p,\ \ P(S_3=2)=3qp^2,\ \ P(S_3=3)=p^3.
$$
数え上げ(組合せ)
$k$ 回成功の並び数は $\binom{3}{k}$、各並びの確率は $p^k q^{3-k}$。ゆえに
$$
P(S_3=k)=\binom{3}{k}p^k q^{3-k}\quad(k=0,1,2,3).
$$
この2つの計算結果は一致します。
漸化式(更新)+外生成分布(確率変数)の融合
- モデル(外生ノイズの導入)
$X_i\in{-1,+1}$ を独立同分布、$P(X_i=+1)=p,\ P(X_i=-1)=q=1-p$ とし、
$$
S_0=0,\qquad S_{n+1}=S_n+X_{n+1}.
$$
ここで $X_{n+1}$ が外生の確率変数(イノベーション)。
ここまでくると、明確に冒頭の畳み込みを処理して、その係数から確率を取得するの意味が分かると思います。
- 3つの“再帰”の顔
- 過程レベル(更新式):$S_{n+1}=S_n+X_{n+1}$(定義そのもの)。
- 分布レベル(畳み込み再帰):$u_n(k)=P(S_n=k)$ とおくと
$$
u_{n+1}(k)=pu_n(k-1)+qu_n(k+1),\qquad u_0(0)=1.
$$ - 母関数レベル(pgf の一次方程式):$G_n(s)=E[s^{S_n}]$ とおくと
$$
G_{n+1}(s)=(qs^{-1}+ps)G_n(s),\qquad G_0(s)=1.
$$
フィボナッチが OGF で「シフト $\Rightarrow$ $x$ 倍」に落ちるのと対応して、ランダムウォークは pgf で「和(畳み込み)$\Rightarrow$ 積」に落ちます。
- 解(分布・モーメント・漸近)
- 分布(閉形式):独立性より
$$
G_n(s)=(q,s^{-1}+p,s)^n
=\sum_{k=0}^{n}\binom{n}{k}q^{k}p^{n-k}s^{n-2k},
$$
よって
$$
P(S_n=n-2k)=\binom{n}{k}p^{n-k}q^{k}\quad(k=0,\dots,n).
$$ - モーメント(pgf から一行):
$$
E[S_n]=G_n'(1)=n(2p-1),\qquad
\operatorname{Var}(S_n)=G_n''(1)+G_n'(1)-{G_n'(1)}^2=4npq.
$$ - 漸近(ド・モアブル=ラプラス):標準化すると
$$
\frac{S_n-n(2p-1)}{2\sqrt{npq}}\ \xrightarrow{d}\ \mathcal{N}(0,1).
$$
- なぜこの枠組みが有効か(要点)
- 統一性:過程→分布→母関数が同じ更新を表現(一次方程式/係数抽出で機械的に処理)。
- 拡張性:$p$ を時点・状態依存 $p_n$ や $p(S_n)$ にすれば、
状態依存再帰/多変量 pgf/行列母関数へ自然に拡張(非復元・ポリア壺・HMM など)。 - 対比の明瞭さ:フィボナッチ(決定的線形漸化式)⇔ランダムウォーク(確率的更新)。
どちらも「母関数=翻訳機」で方程式に落として解き、係数(or 微分)を読む。
まとめ:ランダムウォークは「漸化式(更新)+外生確率変数」として立てると、分布・モーメント・漸近がpgf の一次方程式で一直線に出ます。これは、ド・モアブルが確定・確率の両側で生成関数を“係数を読む計算枠”として使いこなした流儀の、現代的な書き直しです。
確率母関数
確率母関数$G(s)$は、次のように定義されます:
$$G(s) =E(s^X)= \sum_{k=0}^\infty(s^kp(k))=s^0p(0) + s^1p(1) + s^2p(2)+ s^3p(3) + ...---(1)$$
$\Sigma$は無限和を意味し、$k$ は通常0から始まります。確率母関数は、確率変数が取る各離散値 $k$ に対する確率 $p(k)$ と、それに対応する形式的な変数 $s$ の $k$ 乗項 ($s^X$) を組み合わせて定義されます。
定義から分かるように、この式は確率変数 $X$ の期待値 $E(s^X)$ そのものです。$G(s)$ は多項式または級数となることもあります。たとえば、$s=1$のとき上式は
$$G(1)=1^0p(0)+1^1p(1) + 1^2p(2) + 1^3p(3) + ...=p(0)+p(1)+p(2)+p(3)+...$$
です。
期待値と分散
例えば、$G(s)$ の1階微分を $s=1$ で評価することで、確率変数の期待値(平均)を求めることができます。
$G(s) = E[s^X]$を$s$に関して一階微分することを考えます。ここで、$X$は離散確率変数であると仮定し、$p(x)$を$X$が特定の値$x$を取る確率とします。このとき、$G(s)$は以下のように書き表されます:
$$G(s) = E[s^X] = \sum_{x} s^x p(x)$$
この式を$s$に関して微分します。微分の操作は和の中に入れることができるので、各項を$s$に関して微分すると、次のようになります:
$$\frac{dG(s)}{ds} = \sum_{x} \frac{d}{ds}(s^x) p(x)$$
ここで、$s^x$の$s$に関する微分は$x \cdot s^{x-1}$です。したがって、
$$\frac{dG(s)}{ds} = \sum_{x} x \cdot s^{x-1} p(x)$$
これに$s=1$を代入すると$E(X)$となります。
$$E(X)=\frac{dG(s)}{ds}\Big|{s=1}=\sum{x} x \cdot p(x)$$
2階微分は
$$\frac{d^2G(s)}{ds^2} = \sum_{x} x(x-1) \cdot s^{x-2} p(x)$$
となり、これに$s=1$を代入すると、
\frac{d^2G(s)}{ds^2}\Big|_{s=1} = \sum_{x} x(x-1) \cdot p(x) =E[X(X-1)]
が得られます。したがって、
$$E[X^2] = E[X(X-1)] + E[X]$$
となります。最終的に、
$$Var(X) = E[X^2] - [E(X)]^2=\frac{d^2G(s)}{ds^2}\Big|_{s=1}+E(X)-[E(X)]^2$$
を使用して分散を求めることができます。
モーメント母関数(積率母関数)
モーメント母関数は、確率変数の分布を特徴付けるもう一つの重要な数学的手法です。確率変数の分布の特性を、その確率変数のべき乗の期待値の列(モーメント)として捉えます。モーメント母関数 $M(t)$ は、次のように定義されます:
$$M(t) = E[e^{tx}]$$
ここで、$E$ は期待値を意味し、$x$ は確率変数を示します。パラメータ $t$ は任意の実数です。
例えば、$M(t)$ を $t$ のべき級数として展開すると、次のようになります:
$$M(t) = E[e^{tx}] = 1 + tE[x] + \frac{t^2}{2!}E[x^2] + \frac{t^3}{3!}E[x^3] + \ldots$$
この展開から、$E[x]$ は一次モーメント(平均)、$E[x^2]$ は二次モーメント(分散)、$E[x^3]$ は三次モーメント(歪度)といった形でモーメントを求めることができます。
期待値と分散
積率母関数(mgf)$M_X(t)=E[e^{tX}]$ が $t=0$ の近傍で存在・微分可能とすると,
$$
E[X]=M_X'(0),\qquad
\operatorname{Var}(X)=M_X''(0)-{M_X'(0)}^2.
$$
導出(1行ずつ)
- $M_X'(t)=\dfrac{d}{dt}E[e^{tX}]=E[Xe^{tX}]\Rightarrow M_X'(0)=E[X]$。
- $M_X''(t)=\dfrac{d}{dt}E[Xe^{tX}]=E[X^2 e^{tX}]\Rightarrow M_X''(0)=E[X^2]$。
- よって $\operatorname{Var}(X)=E[X^2]-{E[X]}^2=M_X''(0)-{M_X'(0)}^2$。
参考:累積母関数
$$
K_X(t)=\log M_X(t)\quad\Rightarrow\quad
E[X]=K_X'(0),\ \ \operatorname{Var}(X)=K_X''(0).
$$
統計検定一級の2023年の数理の問題3について
Python コードで試しています。
パラメータ $\lambda > 0$ の指数分布に従う確率変数 を$X$ とする。確率密度関数は
$$
f(x) = \begin{cases}
\lambda e^{-\lambda x} & (x > 0) \
0 & (x \leq 0)
\end{cases}
$$
とします。
確率変数 $X_W$ は、$h > 0$ に対して、確率密度関数
$$
g(x) = \frac{e^{hx}f(x)}{M_X(h)} \tag{1}
$$
を持つとします。ただし、$h$ は $M_X(t)$ が存在する $t$ の範囲内に取ることにします。
一般に正値を取る連続型確率変数 $X$ の確率密度関数 $f(x)$ について考えます。
$X$ のモーメント母関数 $M_X(t)$ は区間 $(-\infty, b)$ で存在すると仮定し $(b > 0)$、$-\infty < h < b$ とします。このとき、任意の正の整数 $r$ に対し $M_X(h)$ の $r$ 階微分 $M_X^{(r)}(h)$ は存在するとします。確率変数 $X_W$ の確率密度関数 $g(x)$ を式(1) と同じ式によって定義する。
- 図1:指数分布 $X\sim\mathrm{Exp}(\lambda=2)$ の $h\mapsto E[X_W]=M'(h)/M(h)=1/(\lambda-h)$(理論曲線)と MC 推定(点)
つぎに$g(x)$をガンマ分布を用いて同じように定義します。
- 図2:ガンマ分布 $X\sim\Gamma(k=3,\theta=0.5)$ の $h\mapsto E[X_W]=k\theta/(1-\theta h)$(理論曲線)と MC 推定(点)
どちらも $h$ を増やすと $E[X_W]$ が単調増加しており、$\log M$ の凸性→単調性を視覚的に確認できます。
パラメータや $h$ の範囲、サンプル数はコード中の変数を変えるだけで調整できます。
# -*- coding: utf-8 -*-
"""
追加: h ↦ E[X_W] のプロット(それぞれ単独プロット)
- 分布1: 指数分布 Exp(λ)
- 分布2: ガンマ分布 Gamma(k, θ)
* 解析解(理論曲線)と Monte Carlo 推定(点)を両方描画
* seaborn 不使用、サブプロット不使用、色指定なし
"""
import math
import numpy as np
import matplotlib.pyplot as plt
# ============ 解析用の関数群 ============
def EX_tilt_exp(lmbda, h):
# Exp(λ): E_W[X] = 1/(λ - h), h < λ
return 1.0 / (lmbda - h)
def EX_tilt_gamma_theory(k, theta, h):
# Gamma(k, θ): M(t) = (1 - θ t)^(-k) (t < 1/θ)
# E_W[X] = M'(h)/M(h) = k θ / (1 - θ h)
return (k * theta) / (1.0 - theta * h)
def EX_tilt_mc(samples, h):
# Monte Carlo 推定: E_W[X] = E[X e^{hX}] / E[e^{hX}]
exph = np.exp(h * samples)
num = np.mean(samples * exph)
den = np.mean(exph)
return num / den
# ============ 乱数サンプル ============
rng = np.random.default_rng(12345)
# 指数分布パラメータ
lmbda = 2.0 # E[X]=1/λ=0.5
N_exp = 200_000
exp_samples = rng.exponential(scale=1.0/lmbda, size=N_exp)
# ガンマ分布パラメータ
k, theta = 3.0, 0.5 # E[X]=kθ=1.5
N_gamma = 200_000
gamma_samples = rng.gamma(shape=k, scale=theta, size=N_gamma)
# ============ h グリッド ============
# 収束域に注意: Exp は h < λ, Gamma は h < 1/θ
h_max_exp = lmbda - 0.1
h_max_gamma = 1.0/theta - 0.1
hs_exp = np.linspace(-1.5, min(1.5, h_max_exp), 41)
hs_gamma = np.linspace(-1.0, min(1.5, h_max_gamma), 41)
# ============ 計算(理論とMC) ============
EXW_exp_theory = np.array([EX_tilt_exp(lmbda, h) for h in hs_exp])
EXW_exp_mc = np.array([EX_tilt_mc(exp_samples, h) for h in hs_exp])
EXW_gamma_theory = np.array([EX_tilt_gamma_theory(k, theta, h) for h in hs_gamma])
EXW_gamma_mc = np.array([EX_tilt_mc(gamma_samples, h) for h in hs_gamma])
# ============ 図1: 指数分布 ============
plt.figure(figsize=(8,4))
plt.plot(hs_exp, EXW_exp_theory, label="Theory E_W[X]=1/(λ-h)")
plt.scatter(hs_exp, EXW_exp_mc, s=15, label="MC estimate")
plt.title("Tilted Expectation E[X_W] (Exponential λ=2.0)")
plt.xlabel("h")
plt.ylabel("E[X_W]")
plt.legend()
plt.tight_layout()
plt.show()
# ============ 図2: ガンマ分布 ============
plt.figure(figsize=(8,4))
plt.plot(hs_gamma, EXW_gamma_theory, label="Theory E_W[X]=kθ/(1-θh)")
plt.scatter(hs_gamma, EXW_gamma_mc, s=15, label="MC estimate")
plt.title("Tilted Expectation E[X_W] (Gamma k=3, θ=0.5)")
plt.xlabel("h")
plt.ylabel("E[X_W]")
plt.legend()
plt.tight_layout()
plt.show()
# 端点の検算を数値で出力
print("\n[Check: Exponential]")
for h in [-0.5, 0.0, 0.5, 1.0]:
print(f"h={h:>4}: theory={EX_tilt_exp(lmbda,h):.6f}, MC={EX_tilt_mc(exp_samples,h):.6f}")
print("\n[Check: Gamma]")
for h in [-0.5, 0.0, 0.5, 1.0]:
if h < 1.0/theta: # 収束域のみ
print(f"h={h:>4}: theory={EX_tilt_gamma_theory(k,theta,h):.6f}, MC={EX_tilt_mc(gamma_samples,h):.6f}")
参考
Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。」