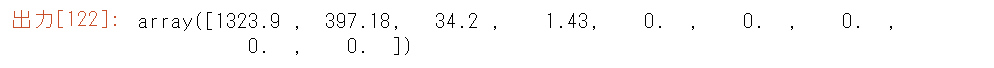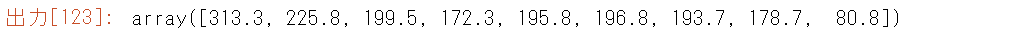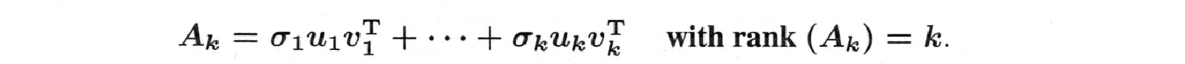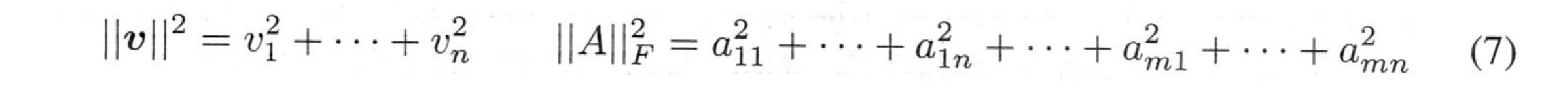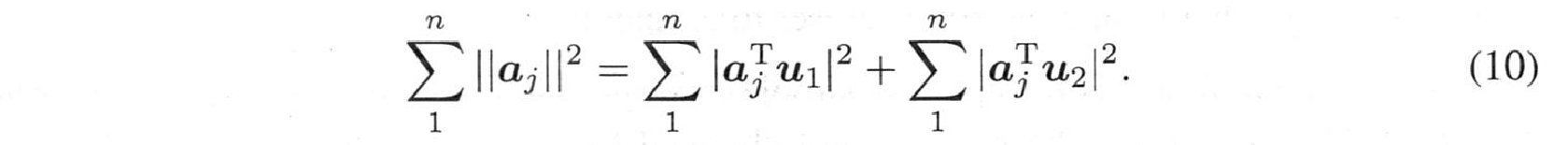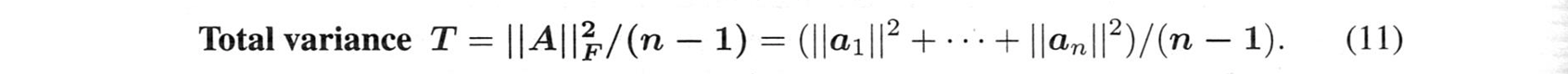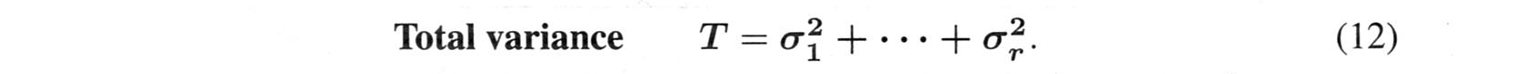ギルバート・ストラング先生の「線形代数入門」の第6版(英語版)が2023年1月に発売されました。総ページ数は440ページで、前の5版の574ページよりもかなり少なくなりました。ちなみに4版の英語版は585ページです。私が持っている5版はカラーで文字も大きく、一方、6版は白黒で文字も小さくなっています。私は5版の特異値分解と主成分分析のところが気に入っていましたが、残念ながら、6版では内容がかなり変更され、主要な部分はコンパクトで分かりやすく、またある部分は詳細に改善されましたが、例題の部分は多くが削除されています。そこで、私は5版の7.3の私のお気に入りの部分を翻訳しそれを記事としてQiitaに載せていました。2023/6/13(4460)に、5版の7.3の一部をけずり6版の関連部分を踏ましました。2023/7/19(4861)に再度削った部分を戻し、さらに解説を加えました。また6版の関連部分は最後に持ってきました。
「線形代数入門」6.1:固有値と固有ベクトル入門
「線形代数入門」7.1:特異値分解
も参考にしてください。
Githubからダウンロード出来ます。
https://github.com/innovation1005/qiita_innovation1005
以下簡易翻訳(節の切り取りのため、読みやすいように一部変更、またPythonで検算)--------------------------------
主成分分析(PCA by SVD)5版の7.3の部分翻訳
- データは$n$個の標本と標本あたり$m$個の測定値からなり行列として与えられます。
- 行列$A$は各測定値と行平均の差(偏差)です。
- SVDは、最も多くの情報を含んでいるデータの組み合わせを見つけます。
- 最大の特異値$\sigma_1$ <-> 最大の分散 <-> $u_1$の情報が最も多いものです。
本節では、SVDの統計学やデータ解析への代表的な応用を説明します。例として、ファイナンスを取り上げます。問題は、データ(=測定値)の大きな行列を理解することです。$n$個の標本のそれぞれについて、$m$個の変数があります。データ行列$A_0$は、$n$個の列と$m$個の行で構成されています。
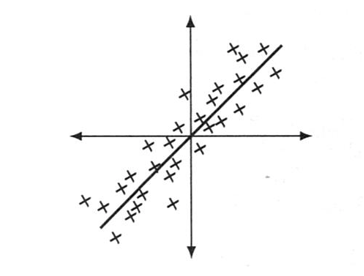
視覚的には、$A_0$の列は$\mathbb{R}^m$における$n$個の点です。各行の平均を引いて$A$を求めると、$n$個の点はしばしば線に沿って塊を形成しているか、あるいは平面(あるいは$\mathbb{R}^m$の他の低次元部分空間)の近いところに集まります。その線、平面、部分空間とは何でしょうか?
数値ではなく、図を用いて説明することから始めましょう。年齢や身長といった$m=2$の変数の$n$個の点は平面$\mathbb{R}^2$上にあります。データは平均年齢と平均身長との差を取り偏差とします。もし、$n$個の偏差が線に沿って集まっているとしたら、線形代数学ではその線をどのように見つけたらよいでしょうか?
図7.2: $A$内のデータ点は、$\mathbb{R}^2$内の直線または$\mathbb{R}^2$内の部分空間に近いことが多い。
$A$は2×n(大きな零空間)
$AA^T$は2×2(小さな行列)
$A^TA$はn×n(大きな行列)
2つの特異値: $\sigma_1>\sigma_2>0$
データ行列を段階を踏んで構成してみましょう。まず、$A_0$ は測定値です。これは標本です。各行の平均$\mu_1,\mu_2,\cdots,\mu_m$ を求めます。$i$行目のデータ点と行平均$\mu_i$ の差を取り偏差を求め、データを中心化します。これで、中央に寄せられた行列$A$の各行の平均は0となります。つまり、図7.2の点(0,0)がn点の真の中心となります。
標本共分散行列は$S=\frac{AA^T}{n-1}$で定義されます。
$A$は各測定値から行平均$\mu_i$までの距離 $a_{ij} - \mu_i$ です。
$AA^T_{11}$と$AA^T_{22}$は距離の二乗和(標本分散$s_1^2$、$s_2^2$)を示しています。
$AA^T_{12}$は標本共分散$s_{12}$=(Aの1行目)・(Aの2行目)となります。
分散は、統計学で重要な値です。試験の平均点が85点であれば、適切な試験であったことがわかります。分散$s^2=25$(標準偏差$s=5$)の場合は、ほとんどの成績が80点台に集中していたことを意味しますし、標本分散$s^2=225(s=15)$の場合は、成績が広く分散していたことを意味します。
数学の試験と歴史の試験の共分散は、平均値と成績の差$A$の行のドット積です。共分散がゼロ以下ということは、1科目が得意でもう一方が不得意ということです。共分散が大きいということは、両方が得意か、または両方が不得意のどちらかです。
統計学者はよく$n$の代わりに$n-1$で割ります。これは自由度の1つが平均値で使われ、$n-1$が自由に変更できるものとして残るからです。いずれにせよ、信頼できる統計であるためには$n$は大きいに越したことはありません。$A$の行が$n$個の入力を持つ場合、$AA^T$の数字の数は$n$とともに伸びていき、$n-1$による除算は、それらに安定性をもたらします。
例1 数学と歴史のスコア(各列の平均値がゼロであることに注目)

の標本共分散は
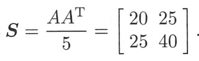
です。
2列の相関が高い場合: $S_{12}=25$. 数学が平均以上であれば、歴史も平均以上のとなる可能性が高くなります。2行目の符号をすべて変えると、負の共分散$s_{12}=-25$となります。$S$は正のトレースと行列式を持ち、$AA^T$は正定値であることに注意してください。
$S$の固有値は約57と3です。つまり、第1番目の$\sqrt{57}u_1v_1^T$は、2番目の$\sqrt{3}u_2v_2^T$より大きく、第一固有ベクトル$u_1$が図7.2の散布図に見られる方向を示しています。その固有ベクトルは、約$u_1=(.6,.8)$になります。
そして、グラフの方向は6-8-10($6^2+8^2=100^2$)または3-4-5を3辺とする右三角形を与えます。
$A$(偏差)のSVDは、散布図において重要な方向を示しています。
第二特異値ベクトル $u_2$ は $u_1$ と垂直です。第二特異値 $\sigma_2 \approx \sqrt{3}$は、方向を示す線に対する広がり具合を示します。もし、$A$の中のデータ点が直線($u_1$方向)上に正確に配置されていたら、$\sigma_2$はゼロになります。実際には、$\sigma_1$しかなくなります。
import numpy as np
from scipy import linalg
A=np.array([[3, -4, 7, 1,-4,-3],
[7, -6, 8, -1,-1,-7]])
A
u, s, vh = np.linalg.svd(A, full_matrices=False)
print("固有ベクトルで構成される行列")
print(u)
print("特異値:",s)
print("vh")
print(vh)
S=A@A.T/5
S
u, s, vh = np.linalg.svd(S, full_matrices=True)
print("Sの固有ベクトルで構成される行列:")
print(u)
print("固有値",s)
print("vh")
print(vh)
print("特異値:",np.sqrt(s*5))
s,u=np.linalg.eig(S)
print("固有値")
print(s)
print("固有ベクトル")
print(u)
主成分分析(PCA)の極意
$m$次元からなる測定データの変数(ここでは年齢と身長)をプロットした際に、PCAは、その解釈を与えてくれます。データ点(要素)と平均年齢と身長の差をとることで、$m×n$($n$個の標本に対して$m=2$)の行列$A$は中心化されています。線形代数との決定的なつながりは、$A$の特異値と特異ベクトルにあります。標本共分散行列$S=AA^T/(n-1)$の固有ベクトル$u$を求めます。
-
データの全分散は、すべての固有値と標本分散$s^2$の和となります。
全分散$T=\sigma_1^2+\cdots+\sigma_m^2=s_1^2+\cdots+s_m^2=トレース(対角要素の和)$ -
$S$の点の第一特異値ベクトル$u_1$ は、データの最も重要な方向を指します。
その方向は全分散のある割合($\sigma_1^2/T$)を占めます。 -
第二特異値ベクトル$u_2$($u_1$に直交する)は、第一特異値ベクトルよりは少ない割合($\sigma_2^2/T$) を説明します。
-
その割合が小さくなれば、そこで止めます。データの大部分を説明する$R$個の方向があります。$n$個のデータ点は、$u_1$から$u_R$の基底を持つ$R$次元の部分空間の周辺にあります。これらの$u$は$m$次元空間における主成分です。
-
$R$は$A$の "実効ランク "であり、真のランク$r$は$m$か$n$です:フルランク行列。
垂直最小二乗法
図7.2の$u_1$方向の線が、垂直最小二乗法(=直交回帰)の解であることはあまり知られていないかもしれませんね。
点から直線までの垂線の距離の二乗和は最小となります。
証明:各列$a_j$を、$u_1$線と$u_2$線に沿った成分に分解します:
右三角形:$\sum_{j=1}^n||a_j||^2=\sum_{j=1}^n|a_j^Tu_1|^2+\sum_{j=1}^n|a_j^Tu_2|^2$ (1)
左側の和はデータ点$a_j$($A$の列)で固定されています。右側の最初の和は$u_1^TAA^Tu_1$です。つまり、PCAで固有ベクトル$u_1$を選んでその和を最大化すると、2番目の和は最小化することになります。この2番目の和(データ点から最良線までの距離の二乗)は、垂直最小二乗法では最小となります。
最小二乗法では、最良の線からy軸に垂直な距離を用いて次のような正規方程式 $A^TA\hat{x}=A^Tb$ に到達しました。
PCAでは最良の線に垂直な距離を使うことで$u_1$の固有値問題とします。"完全最小二乗法 "では、$b$だけでなく$A$の誤差も許容されます。
標本相関行列
データ解析は、主に$A$(中心化データ)を使って行われますが、$A$の測定値には、次のようなものがあります。インチやポンド、年やドルといった異なる単位。1組の単位を変更する(インチをメートルに、年を秒に)と、その行の$A$や$S$に大きな影響を与えます。尺度変換として、共分散行列$S$から相関行列$C$に変更します:
対角行列$D$は$A$を尺度変換します。$D A$の各行は長さ$\sqrt{n-1}$です。
標本相関行列 $C=DAA^TD/(n-1)$ は対角線上に1があります。
「確率と統計」では、期待共分散行列$V$と期待相関行列(対角成分が1)を用います。これらは、実際の測定値の代わりに確率を使います。共分散行列は、将来の測定値の平均値からの広がりを予測するもので、$A$と標本共分散$S$と相関行列$C=DSD$は、実データを使います。いずれも統計学と正定値行列の線形代数、SVDとの大きな接点であり、非常に重要です。
金融におけるPCA: 金利のダイナミクス(5版7.3の例)
金融数学では、常に線形代数とPCAが適用されます。ここでは、財務省証券のイールドカーブの応用例を紹介します。「イールド」とは、債券や中期証券、短期証券に支払われる金利のことです。その金利は、満期までの時間によって異なります。長い債券(3年~20年)の場合、金利は長さに応じて上昇します。連邦準備制度理事会は、経済を減速させたり刺激したりするために、短期の利回りを調整します。以上がイールドカーブで、リスク管理者やトレーダー、投資家が利用するものです。
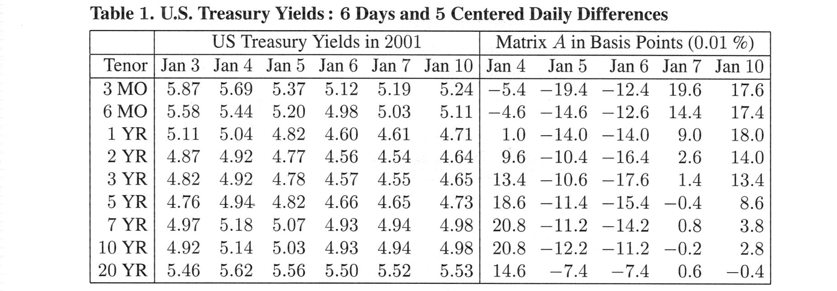
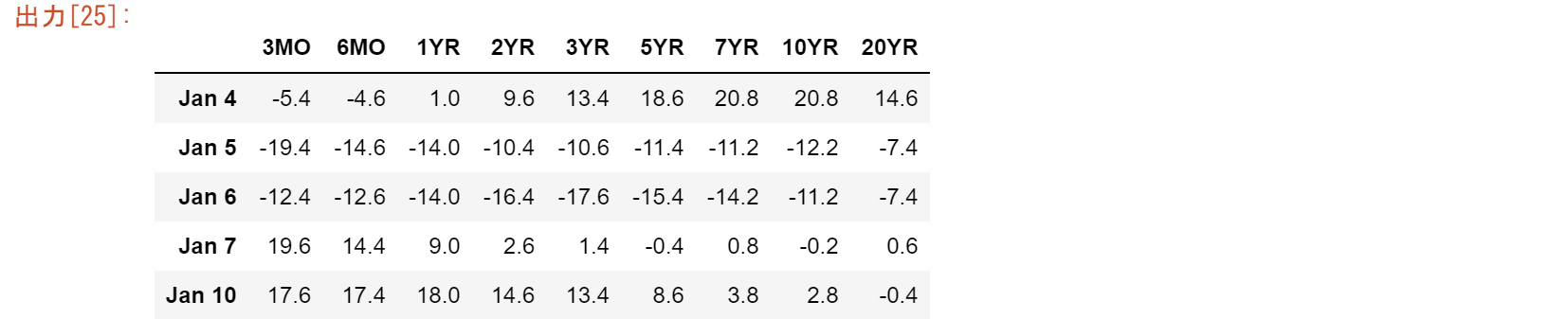
以下は、2001年の最初の6営業日のデータです。各列は、ある特定の日の実際のイールドカーブです。満期までの期間が「テナー」です。左側の6列は金利で、日ごとに変化します。右側の5列は日ごとの金利差で、各行と平均値の差です。$A$は、行を加算すればゼロになる中心化された行列です。実際のアプリケーションでは、5日や6日ではなく、252営業日(1週間ではなく1年)などです。
import pandas as pd
A=np.array([[5.87,5.69,5.37,5.12,5.19,5.24],
[5.58,5.44,5.20,4.98,5.03,5.11],
[5.11,5.04,4.82,4.60,4.61,4.71],
[4.87,4.92,4.77,4.56,4.54,4.64],
[4.82,4.92,4.78,4.57,4.55,4.65],
[4.76,4.94,4.82,4.66,4.65,4.73],
[4.97,5.18,5.07,4.93,4.94,4.98],
[4.92,5.14,5.03,4.93,4.94,4.98],
[5.46,5.62,5.56,5.50,5.52,5.53]])
A=pd.DataFrame(A,index=['3MO','6MO','1YR','2YR','3YR','5YR','7YR','10YR'\
,'20YR'],columns=['Jan 3','Jan 4','Jan 5','Jan 6','Jan 7','Jan 10'])
A
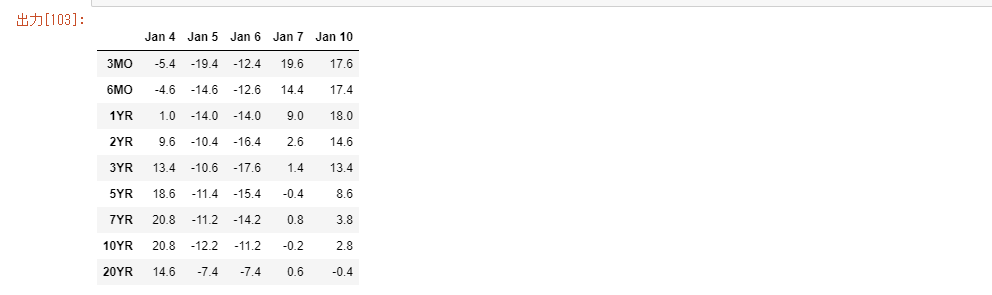
dA=A.T.diff().dropna()
diff=((np.identity(5)-1/5*np.ones((5,5)))@dA).T.values*100
diff=pd.DataFrame(diff,index=['3MO','6MO','1YR','2YR','3YR','5YR','7YR','10YR'\
,'20YR'],columns=['Jan 4','Jan 5','Jan 6','Jan 7','Jan 10'])
diff
5つの列があれば、5つの特異値が期待できます。しかし、5列のベクトルは0ベクトルに加算されます。これは中心化されたAの各行は加算してゼロになるためです。つまり、$S=AA^T/(5-1)$は0以外の4つの固有値
$\sigma_1^2>\sigma_2^2>\sigma_3^2>\sigma_4^2$
を持ちます。ここで、固有値$\sigma_i$とその2乗$\sigma_i^2$と全分散$T=\sigma_1^2+\cdots+\sigma_4^2=\text{trace of S}$との割合を示します。

割合は各主成分($S$の各固有ベクトル$u_i$)によって「説明」されます。
np.set_printoptions(precision=2)
np.set_printoptions(suppress=True) #suppressは禁止の意味
S=diff@diff.T/(5-1)
u,s,vh=np.linalg.svd(S, full_matrices=True)
s
np.set_printoptions(precision=2)
np.set_printoptions(suppress=True) #suppressは禁止の意味
u,s,vh=np.linalg.svd(diff, full_matrices=False)
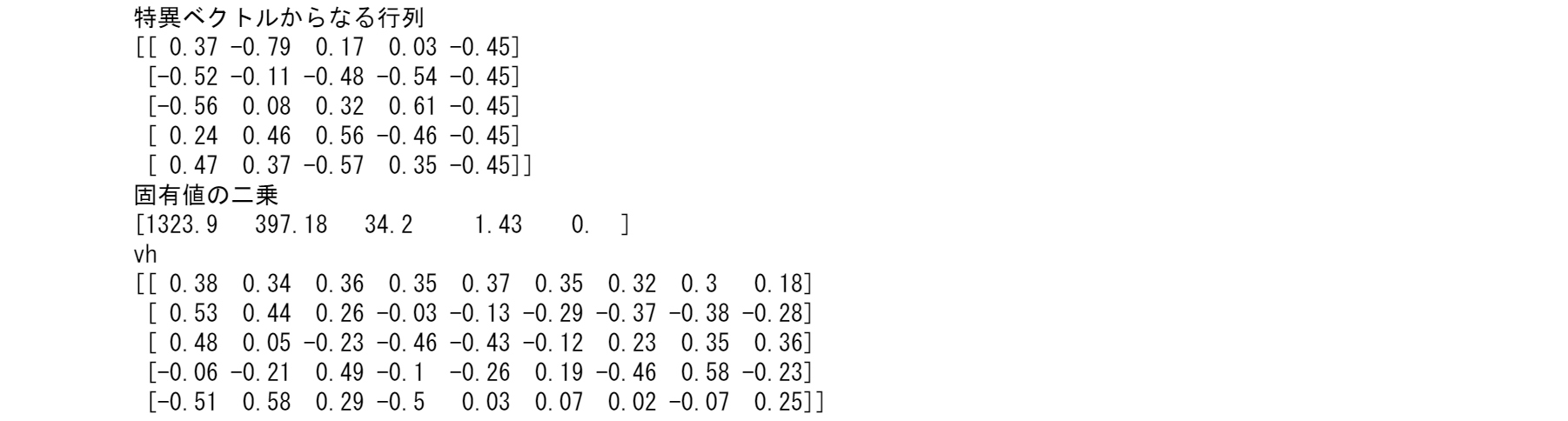
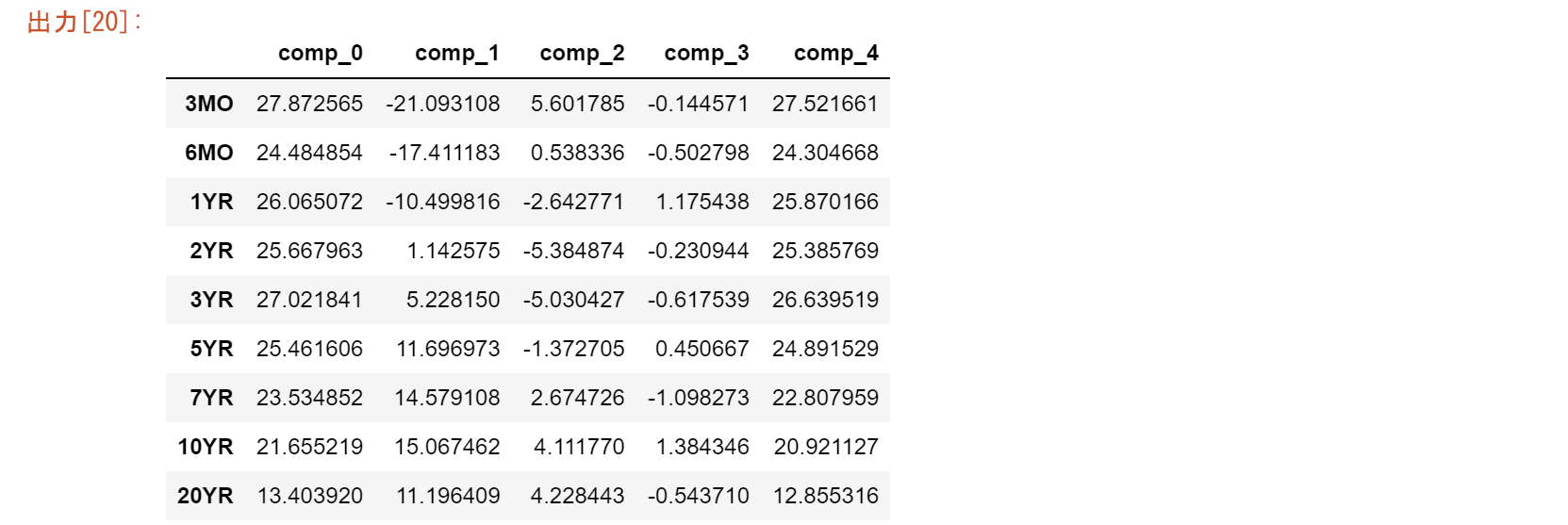
print("特異ベクトルからなる行列")
print(u)
print("固有値の二乗")
print(s*s/4)
print('vh')
print(vh)
「スクリープロット」は、これらの分数$\sigma_i^2/T$が急速にゼロになる様子をグラフ化したものです。大きな問題では、早く落ちた後、底が平坦になります($\sigma^2=0$付近)。
この2つの部分(有意なPCと有意でないPC)の間の転換点を見つけることが重要です。
また、各主成分を解釈することが目的となります。$A$の特異ベクトル$u_i$はSの固有ベクトルです。
そのベクトルの入力が「負荷量」です。このイールドカーブの例($Su_5=0$とする)の$u_1$から$u_5$を表示します。($u_5$が上述の計算と一致しません。これは第5固有値がゼロであるために、ゼロ空間にあるからです。)
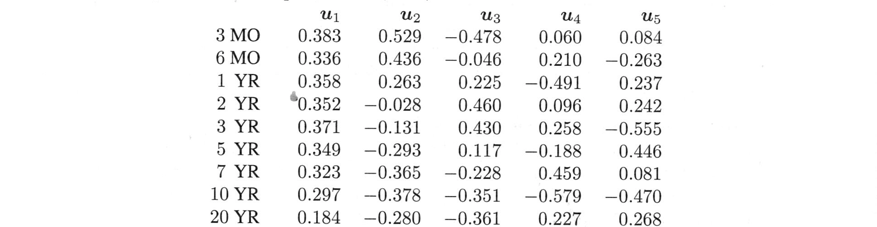
この5つの$u$は、正規直交ベクトルです。$A$の4次元列空間と$A^T$の1次元ゼロ空間の基底となります。この5つの$u$は、どのような金融上の意味を持つのでしょうか?
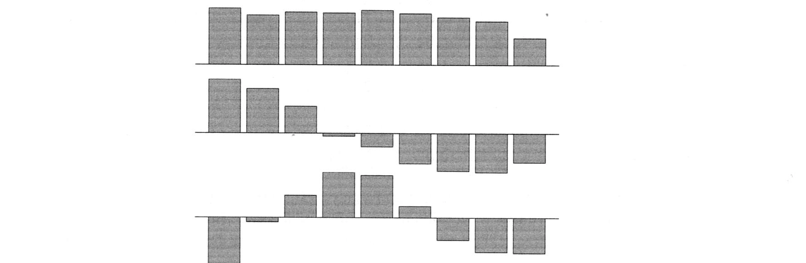
- $u_1$は、9つの利回りの日々の変化の加重平均を測ります。
- $u_2$ は債券の長短のイールドスプレッドの日次変化を測ります。
- $u_3$ は曲率の日変化(短・長債対中)を示します。
つぎのグラフは、上記の$u_1,u_2,u_3$の3ヶ月から20年までの9つの負荷量を示しています。
一般的なアプリケーションではさらに2つの表が含まれます。
一つは、右特異ベクトル$v_i$を示すものです。
$A^TA$の固有ベクトルです。
ベクトル$A^Tu$に比例します。
5つの成分があり、1週間の利回りと短長スプレッドの動きを示します。
分散 $T=1756.7$ (トレース $\sigma_1^2+\sigma_2^2+\sigma_3^2+\sigma_4^2$) は、$S$の対角成分の和でもあります。
これらは$A$の行の標本分散でもあります。
以下はその例です:
$s_1^2+\cdots+s_9^2=313.3+225.8+199.5+172.3+195.8+196.8+193.7+178.7+80.8=1756.7.$
すべての$s^2$は$\sigma_1^2$以下です。また、1756.7は$A^TA/(n-1)$のトレース:行分散です。
なお、この節では、$A$の中心化された行を扱っています。
あるアプリケーション(金融など)では、通常、行列は転置され、列が中心化されます。
そして、標本共分散行列$S$は$A^TA$を使い、$v$が重要な主成分となります。
実用的な解釈を伴う線形代数は、私たちに多くのことを教えてくれます。
np.diag(S)
エンコーディングとデコーディング
scores = np.dot(u, np.diag(s)) # 主成分スコア
scores
loadings = vh.T # 主成分負荷量
n_components = 3
scores_reduced = scores[:, :n_components]
scores_reduced
import matplotlib.pyplot as plt
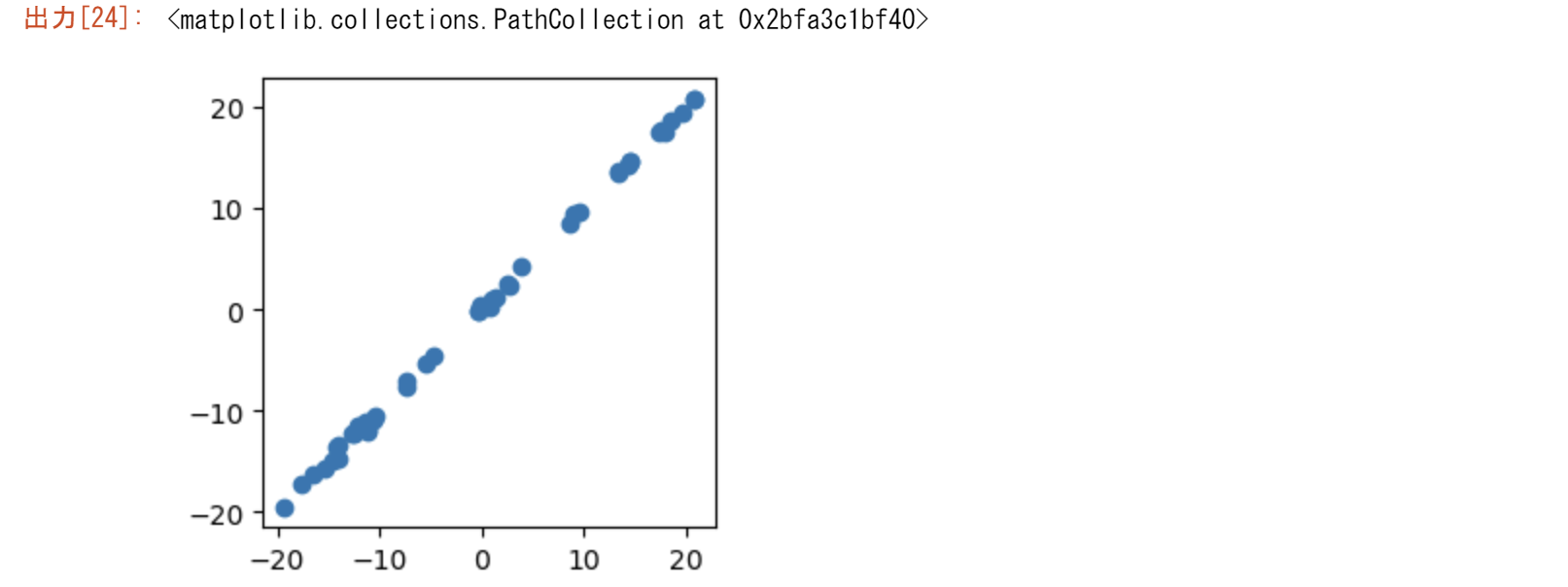
diff_reconstructed = np.dot(scores_reduced, loadings.T[:n_components, :])
diff_reconstructed
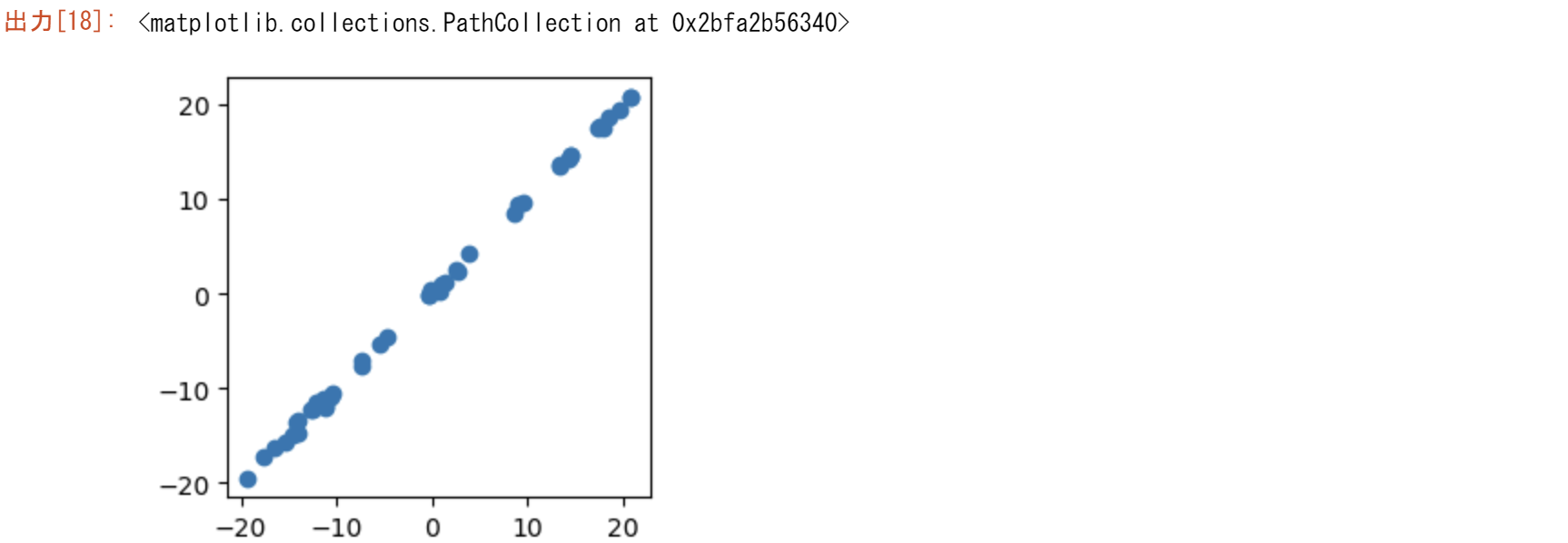
plt.figure(figsize=(3,3))
plt.scatter(diff,diff_reconstructed)
入力行列の転置
主成分分析でも、特異値分解でも行列の向きが結果に影響を与えます。ストラング先生のイールドカーブの例でいうと、通常の逆になっています。要因を列に、観測値を行に取るのが普通です。最終的に正方行列の分散共分散をとって、その固有値と固有ベクトル、特異値と特異ベクトルを取るので、列と行は関係ないように思えます。その違いを主成分分析に特化したPCAと汎用のsvdを用いて理解します。
こちらの方法が一般のPCAであるので違いを試してみる。
dif=diff.T
dif
u,s,vh=np.linalg.svd(dif, full_matrices=False)
print("特異ベクトルからなる行列")
print(u)
print("固有値の二乗")
print(s*s/4)
print('vh')
print(vh)
scores = np.dot(u, np.diag(s)) # 主成分スコア
scores
n_components = 3
scores_reduced = scores[:, :n_components]
scores_reduced
import matplotlib.pyplot as plt
loadings = vh.T # 主成分負荷量
dif_reconstructed = np.dot(scores_reduced, loadings.T[:n_components, :])
dif_reconstructed
plt.figure(figsize=(3,3))
plt.scatter(dif,dif_reconstructed[:])
statsmodelsのPCAを用いた確認
pc = PCA(dif, ncomp=3, method='nipals',standardize=False, demean=False, normalize=False)
pc.factors
from statsmodels.multivariate.pca import PCA
pc = PCA(diff, ncomp=5, method='nipals',standardize=False, demean=False, normalize=False)
pc.factors
svdで行ったPCAと結果が同じになるのが分かります。つまり、行と列を入れ替えると結果は異なります。元のデータと分析の目的を明確にして、行列の形を決めるべきです。金融の場合、行が観測値で列が要因として分析しがちですが、注意が必要です。
6版の7.3 主成分分析(PCA by SVD)
$A$の「主成分」とは、行列$U$と$V$の直交列$u_j$と$v_j$のことでそれらは特異ベクトルです。本節では、特異値分解 $A=U\Sigma V^T$ を適用します。主成分分析(PCA)は、最初の$u$と$v$に結びつく最大の$\sigma$を使用して、データの行列に含まれる情報を理解します。
行列$A$が与えられ、その最も重要な部分である$A_k$(最大の$\Sigma$の部分)を抽出します:
$A_k$は行列の最適化問題を解くので、まずはそこから始めます。$A$に最も近いランク$k$の行列は$A_k$です。統計学では、$A$のうち、分散が最も大きいランク1の部分を特定することになります。
このことから、SVDはデータサイエンスの中心に位置づけられます。
この世界では、PCAは「教師なし」学習なのです。SVDは$A_k$を選択するよう指示します。教師ありの学習では、大きな学習データセットが必要です。
ディープラーニングは、そのデータの大部分を正しく分類するための(非線形!)関数$F$の構築に用います。そして、データ学習といわれる方法を使用するとき、この$F$を新しいデータに適用するのです。
主成分分析の$A_k$による行列近似法に基づく証明は、Schmidt(1907)によって始められました。彼は関数空間の演算子について書いています; 彼の考えはそのまま行列に拡張されます。Eckart と Young は新しい証明の$A-A_k$ を測るのにフロベニウス規範を使っています。そして、Mirsky は、以下の定義 (2), (3), (4) のように特異値のみに依存するノルム$||A||$について考えました。
ここで、特殊なランク$k$行列の重要な性質は次の通りです。
$A_k=\sigma_1u_1v_1^T+\cdots+\sigma_ku_kv_k^T$:
$B$がランク$k$で$||A-A_k||\le ||A-B||$であれば、$A$に最も近い$A_k$です。
行列ノルム$||A||$の3つの選択肢には特別な重要性があり、独自の名前がついています:
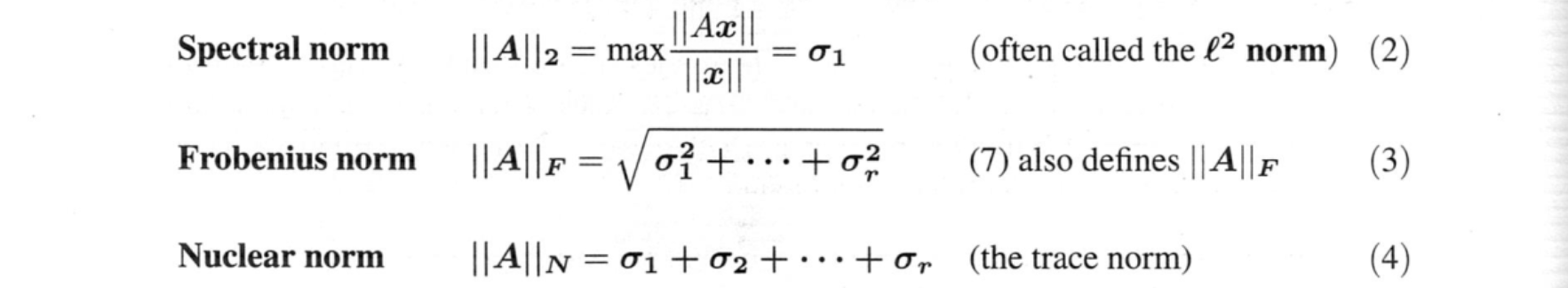
これらの規範は、$n$×$n$の恒等式行列に対して、すでに異なる値を持っています:
$||I||_2=1 ||I||_F=\sqrt{n}. ||I||_N=n. \text{ } (5)$
$I$を任意の直交行列$Q$に置き換えても、ノルムは変わりません(すべて$\sigma_i=1$だからです):
$||Q||_2=1 \text{ } ||Q||_F=\sqrt{n} \text{ } ||Q||_N=n \text{ } (6)$
となります。これより、$A$に直交行列を(両側から)掛けても、任意の行列のスペクトルノルム、フロベニウスノルム、核ノルムは変わりません。つまり、$A=U\Sigma V^T$のノルムは、$U$と$V$が直交行列なので、$\Sigma:||A||=||\Sigma||$のノルムと等しくなります。
行列のノルム
ベクトルや行列の大きさを測定する方法が必要です。ベクトルでは、最も重要なノルムは通常の長さ$||v||$です。行列の場合、フロベニウスは二乗和の考え方を拡張し、$A$のすべての入力を含むようにしました。このノルム $||A||_F$ は ヒルベルト・シュミット とも呼ばれます。
明らかに$||v||\ge 0$と$||cv||=|c|\text{ }||v||$です。同様に $||A||_F \ge 0$ と $||cA||_F$ です。同様に欠かせないのが、$v+w$と$A+B$の三角不等式です。
三角不等式 $||v+w||\le ||v||+||w||$と$||A+B||_F\le ||A||_F+||B||_F (8)$
ドット積 $v^Tw$ や行列積 $AB$ に出会ったとき、もう一つの事実を使います。
シュワルツの不等式 $|v^Tw|\le ||v|| ||w|| $と$||AB||_F\le ||A||_F||B||_F (9)$
そのフロベニウス行列の不等式は、シュワルツのベクトルの不等式から直接来ています:
$|(AB)_{ij}|^2\le || Aのi列||^2||Bのj列||^2$ 全$i,j$を加えると$||AB||_F^2$
これは、行列のドットプロダクトが存在する可能性を示唆しています。それは $A \dot B=\text{trace}(A^TB)$ です。
注:$A$の固有値の最大の$|\lambda|$は受け入れ可能なノルムではありません!
非ゼロ行列は、すべてゼロとなる固有値を持つ可能性がありますが、ノルム $||A||$ がゼロであることはありえないことがわかっています。この点で、特異値は固有値より優れています: $\sigma_1=||A||_2$.
エカート・ヤング定理(Eckart-Young Theorem)
定理は式(1)にある:Bがランク$k$なら$||A-A_k||\le ||A-B||$となります。
3つの規範$||A||$と$||A||_F$と$||A||_N$では、$k$項以降のSVDを切ることで$A$に最も近づくことができます。最も近い行列は$A_k=\sigma_1u_1v_1^T+\cdots+\sigma_ku_kv_k^T$です。
これは、$A$を低ランクの行列で近似する際に使う事実です!
対角行列$A$という極めて単純な例題をここで使ってみましょう。
A=\left[\begin{array}{c,c,c,c}
4,0,0,0\\
0,3,0,0\\
0,0,2,0\\
0,0,0,1
\end{array}\right]
に最も近いランク2の行列は
A_2=\left[\begin{array}{c,c,c,c}
4,0,0,0\\
0,3,0,0\\
0,0,0,0\\
0,0,0,0
\end{array}\right]
です。差分$A-A_2$は、2と1を除いてすべて0です。そのとき $||A-A_2||_F=\sqrt{2^2+1^2}$.この$A_2$より$A$に近いランク2の行列が他にあるでしょうか。
この単純な例には、$Q_1Q_2$の形の行列がすべて含まれていることに注意してください。
直交行列 $Q_1$,$Q_2$ によって、ノルムやランクが変わることはありません。
つまり、この例では特異値4,3,2,1を持つすべての行列が含まれます。最良の近似値$A_2$は4と3を保っています。いくつかの証明はLinear Algebra and learning from Data (Wellesley-Cambridge Press)にまとめられています。Chi-Kwong Liは$A_k$が$A$に最も近いというMirskyの証明を$||A||_2$ や$||A||_F$のように$\sigma$にのみ依存するすべての規範に対してして単純化しています。
主成分分析
では、SVDの使い方を説明します。行列$A$にはデータがいっぱい入っています。サンプルは$n$個あります。各サンプルに対して、$m$個の変数(身長や体重など)を測定しています。データ行列 $A_0$ は $n$列、$m$行です。多くのアプリケーションでは、これは非常に大きな行列です。
まず、$A_0$の各行に沿った平均(標本平均)を求めます。その平均を、その行のすべての $m$ 個の入力から引きます。ここで、中心化された行列$A$ の各行は、平均がゼロです。$A$の列には$\mathbb{R}^m$の$n$個の点があります。中央揃えなので、$n$個の列ベクトルの和は0になります。つまり、平均的な列はゼロベクトルです。
これらの $n$ 点は、直線や平面などの低次元空間に集まっていることが多くなります。$\mathbb{R}^m$の部分空間の近くに集まっていることが多くなります。図7.4は、$\mathbb{R}^2$の線上に集まった典型的なデータ点の集合を示しています。($A_0$を中心にして左右上下にずらした後、$A$の平均は(0,0)になります)。
線形代数は、(0,0)を通る最も近い直線をどのように求めるかということです。それは$A$の第一特異ベクトル$u_1$の方向です。これがPCAの重要なポイントです!
図7.4:データ点(の列)は、$\mathbb{R}^2$の直線や$\mathbb{R}^m$の部分空間の近くにあることが多い。
$A$は2×n(大きな零空間)
$AA^T$は2×2(小さな行列)
$A^TA$はn×n(大きな行列)
2つの特異値: $\sigma_1>\sigma_2>0$
PCAを支える幾何学
図7.4の最良の直線は、垂直最小二乗法の問題の解として得ます。これは直交回帰とも呼ばれます。これは、標準的な最小二乗法による $n$ データ点の適合や、線形システム $Ax=b$ の最小二乗法の解とは異なります。この古典的な問題は、$||Ax-b||^2$を最小化します。これは、最良の線に対する上下の距離を測定するものです。今回の問題は、垂直方向の距離を最小化するものです。線形回帰の問題では、最適な$A^TA\hat{x}=A^Tb$の一次方程式が導かれました。今回の問題では、特異ベクトル$u_i$($AA^T$Tの固有ベクトル)が導かれます。これは線形代数の2つの側面であり、同じ側面ではありません。
データ点から $u_1$ 線までの距離の二乗和は最小になります。
これを見るには、$A$の各列$a_j$を$u_1$と$u_2$に沿った成分に分離します:
左の和は、データによって固定されています。右側の最初の和は、項 $u_1^Ta_ja_j^Tu_1$ を持ちます。これは$u_1^T(AA^T)u_1$に加算されます。そこで、PCAでその和を最大化するために、一番上の固有ベクトルを選び$AA^T$の固有ベクトル$u_1$を選び、2番目の和を最大化するのです。データ点から最良の直線(または最良の部分空間)までの距離の二乗和は、可能な限り小さくなるのです。
エッカート・ヤングの幾何学的な意味
図7.4は2次元で、最も近い線になります。さて、データ行列$A_0$が3×$n$だとします: $n$個のサンプルについて、年齢、身長、体重のような3つの測定値があります。ここでも行列の各行を中央揃えにして、$A$のすべての行の足し算が0になるようにします。そして、点は3次元に移動します。
まだ、一番近い線を探すことができます。それは$A$の第一特異ベクトル$u_1$によって明らかになります。一番いい線は(0,0,0)を通るでしょう。しかし、図7.4と比べてデータ点が扇状に広がっている場合は、本当に最良の平面を探す必要があります。「最良」の意味は、やはりこれです:最良の平面に対する垂直距離の二乗の和が最小になるということです。
その平面は特異ベクトル$u_1$と$u_2$を張ったものです。これがEckart-Youngの意味です。
すっきりした結論です: 最良の平面には最良の線が含まれます。
PCAを支える統計学
5版と内容がほぼ同じのため割愛
PCAを支える線型代数学
主成分分析は、$m$次元空間の$n$個の標本点$a_1,\cdots,a_n$データを理解するためのものです。このデータのプロットは、$A$のすべての行がゼロになるように中心を定めています。線形代数との関係は、特異値と左特異点にあります。$A$の特異値と左特異ベクトル$u_i$にあります。
これらは、$A$の固有値$\lambda_i=\sigma_i^2$と、$A$の固有ベクトルに由来します。
サンプル共分散行列 $S=AA^T/(nー1)$の固有ベクトルです。
データの全分散は$A$のフロベニウスノルムの2乗に由来します:
これは$S$のトレース(対角線上の和)です。線形代数では、トレースは標本共分散行列$S$の固有値の和に等しいことがわかります。
SVDは、データを相関のない(共分散がゼロの)断片に分離する特異ベクトル$u_i$を生成しています。これらは分散の小さい順に並んでおり、最初の部分から知るべきことがわかります。
$S$のトレースは、全分散を主成分の分散の和に結びつけます。$u_1,u_2 \cdots,u_r$の主成分の分散の総和につながります.
第一主成分$u_1$は、全分散の何分の一かの$\sigma_1^2/T$を占めます(あるいは「説明します」)。
次の特異ベクトル$u_2$は、次に大きな分散$\sigma_2^2/T$を説明します。
それぞれの特異ベクトルは、行列の意味をとらえようと最善を尽くしており、それがすべて成功しています。
エッカート・ヤング定理のポイントは、$k$個の特異ベクトルが(一緒に作用して)他の$k$個のベクトルセットよりもデータの多くを説明する、ということです。だから、$u_1$から$u_k$を、$n$データ点に最も近い$k$次元部分空間の基底として選ぶことが正当化されるのです。
$A$と$S$の「実効ランク」は、その点より上の特異値の数です。ノイズがデータ中の真のシグナルをかき消す場所です。この点は、特異値(またはその二乗$\sigma^2$)の落差を示す「スクリープロット」上に現れることが多くなります。スクリープロット(図7.2)で、信号が終わり、ノイズが引き継ぐ「エルボー」を探してみてください。
u, s, vh = np.linalg.svd(S, full_matrices=True)
u,s,vh,np.sqrt(s*5)
u, s, vh = np.linalg.svd(A, full_matrices=False)
u,s,vh
s,u=np.linalg.eig(S)
s,u,np.sqrt(s*5)
おまけ 空間
$Ax=b$の列空間を$b$とします。xxは一様乱数です。それに第一固有値を満たす固有ベクトルを条件にして得られる第一固有ベクトルを探します。$(A-I\lambda)x=0$なので、$A-I\lambda=0$. 第一固有ベクトルは右肩上がりの直線になります。第一固有ベクトルはx1=(0.87,0.55)でもいいし、(0.6,0.4)でもOKでした。解は零空間にあり、第一固有ベクトルが特解だからです。伸び縮みするベクトルです。
fig = plt.figure(figsize = (3, 3))
xx=np.random.rand(10000,2)*2-1
A=np.array([[0.8,0.3],
[0.2,0.7]])
b=[]
b2=[]
for x1,x2 in zip(np.transpose(xx)[0],np.transpose(xx)[1]):
b0=(A@np.array([x1,x2]))[0]
b1=(A@np.array([x1,x2]))[1]
b.append([b0,b1])
lamda=1
if np.floor(b0*1000)==np.floor(x1*lamda*1000)\
and np.floor(b1*1000)==np.floor(x2*lamda*1000):
b2.append([b0,b1])
b=np.array(b)
b2=np.array(b2)
plt.scatter(b[:,0],b[:,1])
plt.scatter(b2[:,0],b2[:,1])
第二固有ベクトルも直線になりますが、第一固有ベクトルに直交しています。
b=[]
b2=[]
for x1,x2 in zip(np.transpose(xx)[0],np.transpose(xx)[1]):
b0=(A@np.array([x1,x2]))[0]
b1=(A@np.array([x1,x2]))[1]
b.append([b0,b1])
lamda=0.5
if np.floor(b0*1000)==np.floor(x1*lamda*1000) \
and np.floor(b1*1000)==np.floor(x2*lamda*1000):
b2.append([b0,b1])
b=np.array(b)
b2=np.array(b2)
fig = plt.figure(figsize = (3, 3))
plt.scatter(b[:,0],b[:,1])
plt.scatter(b2[:,0],b2[:,1])
plt.show()
実は
if np.floor(b0*1000)==np.floor(x1*lamda*1000)\
and np.floor(b1*1000)==np.floor(x2*lamda*1000):
b2.append([b0,b1])
この部分は近似計算をしています。正確に=のものを探すことは至難の業で、百万個の乱数を発生しても見つからないでしょう。固有値、固有ベクトルはそれほどまれな事象を表現しているのです。ですから主成分分析で次元圧縮しても元のデータを復元できるのです。
Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。