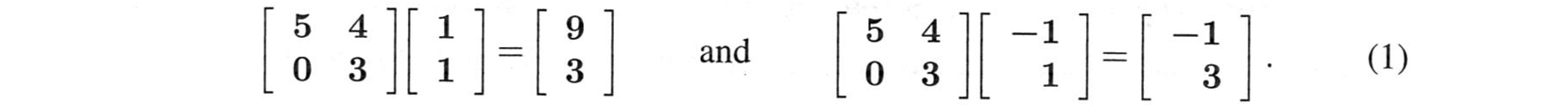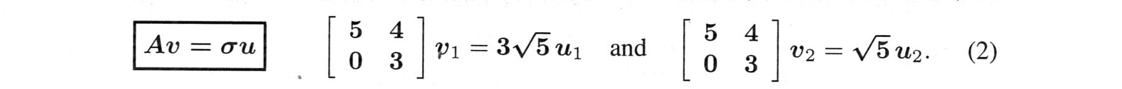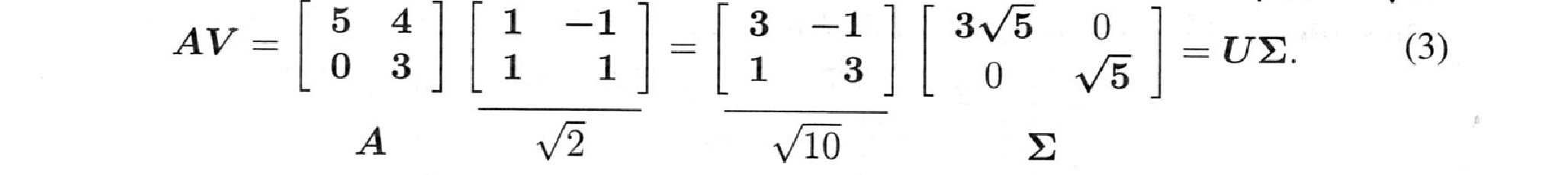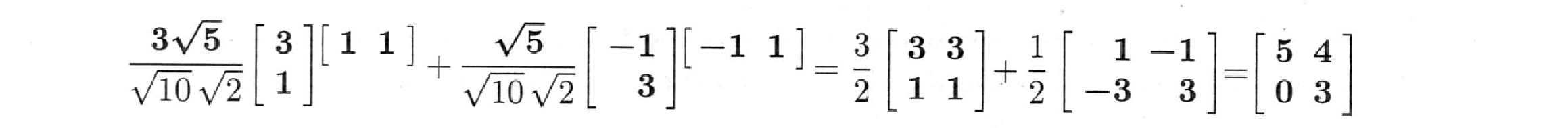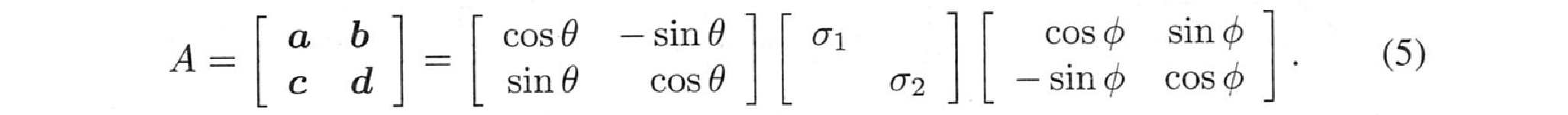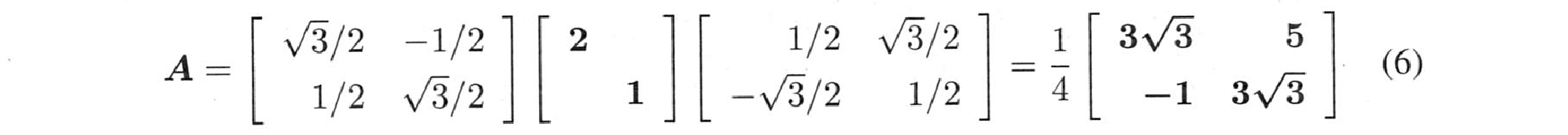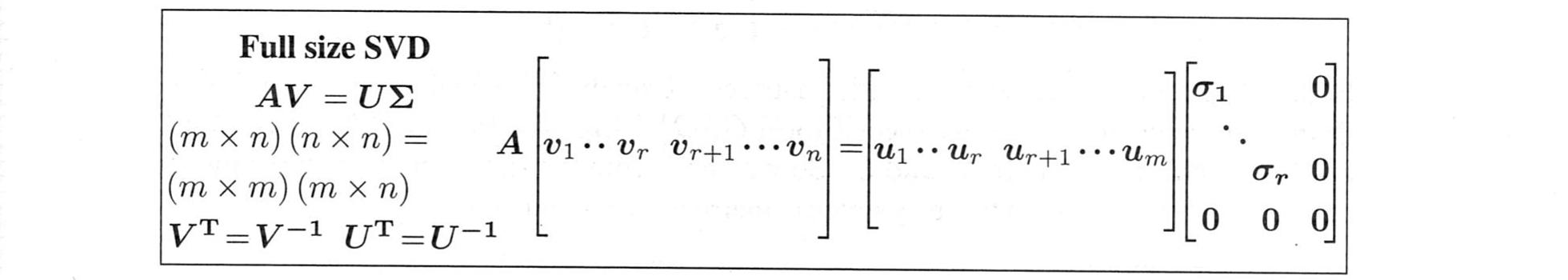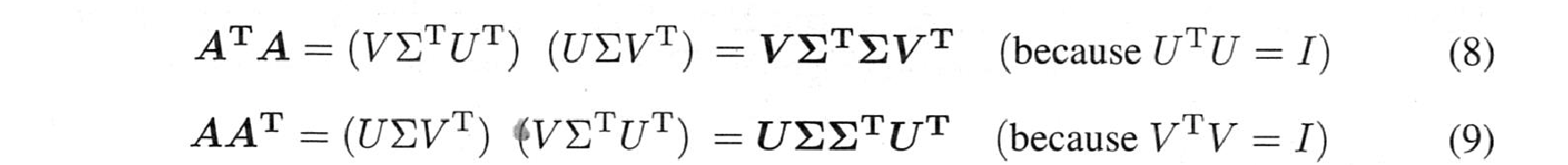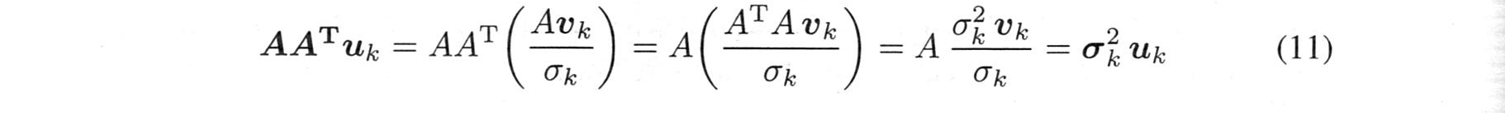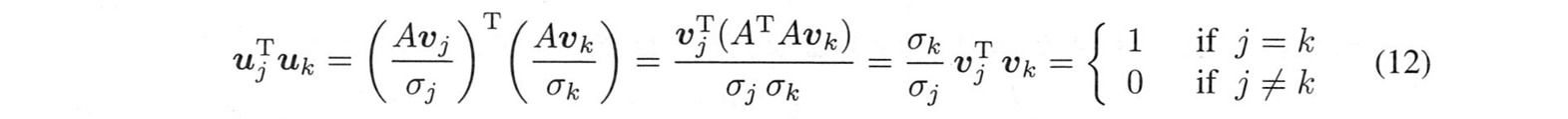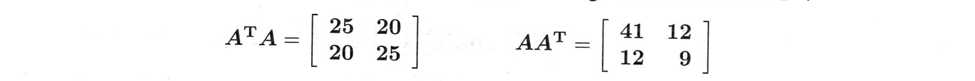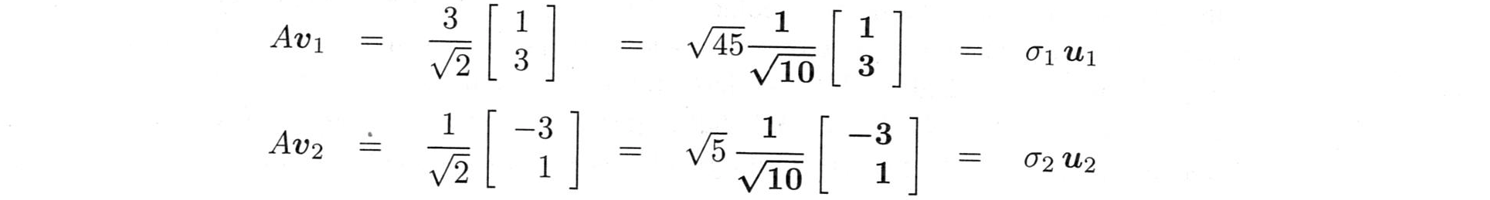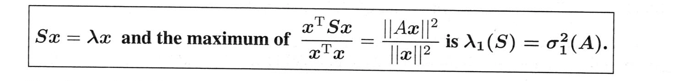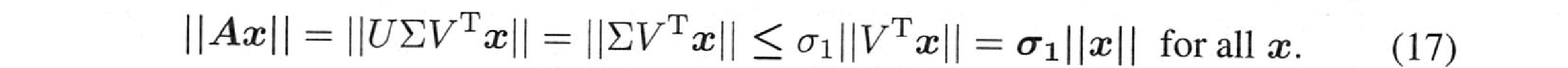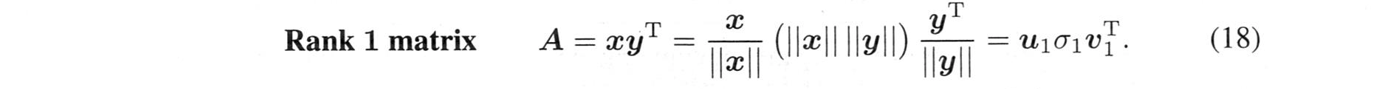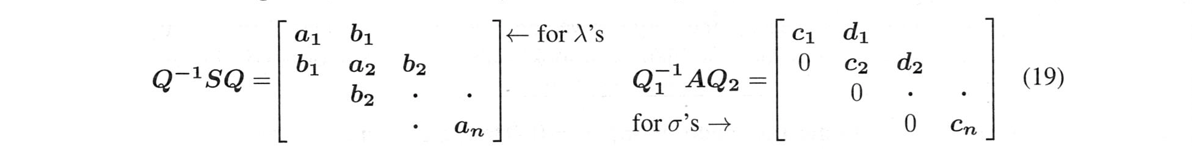ストラング先生のIntroduction to Linear Algegraは6版になりました。世界標準の線形代数の入門書として不動の地位を築いている本書ですが、版を重ねるごとに内容が少しづつ修正されています。
4版の日本語版では、6.7特異値分解としての記述と7.3の対角化と疑似逆行列の項として特異値分解があるだけでしたが、英語の5版になると7章が特異値分解となり、
7.1 Image Processing by Linear Algebra
- Low Rank Images
- Eigenvectors for the SVD
7.2 Bases and Matrices in the SVD
- Proof of the SVD
- An Example of the SVD
- An Extreme Matrix
- Singular Value Stability versus Eiegenvalue Instability
- Singular Vectors of A and Eigenvectors of $S=A^TA$
- Computing the Eigenvectors of S and the Singular Value of A
7.3 Principal Component Analysis
- The Essentials of Principal Component Analysis(PCA)
- Perpendicular Least Squares
- The Sample Correlation Matrix
- Genetic Variation in Europe
- Eigenfaces
- Application of Eigenfaces
- Model Order Reduction
- Searching the Web
- PCA in Finance: The Dynamics of Interest Rates
7.4 The Geometry of the SVD
- The Norm of a Matrix
- Polar Decomposition $A=SQ$
- The Pseudoinverse $A^+$
- Least Squares with Dependent Columns
という構成となりました。6版ではさらに変更されました。
特異値分解の記述はLinear Algebra and Learning from Data(ストラング:線形代数とデータサイエンス:日本語版)の1.8 Singular Values and Singular Vectors in the SVD(特異値分解による特異値と特異ベクトル)にもあります。内容は一部完全に重複するものがありますが、6版に無いものもあります。無いものは
The Important Fact for Data Science(データサイエンスにおいて重要な事項)
The SVD for derivaties and Integrals(微分と積分に対する特異値分解)
Finite Di1fferences(有限差分)
The Polar Decomposition $A=QS$(極分解)
です。また、6版にしかないものもあります。
6版の目次です。
7.1 Sigular Values and Sigular Vectors
- The Geometry of the SVD
- The Full Size Form of the SVD
- The Reduced Form of the SVD
- Proof of the SVD
- AB and BA:Equal Nonzero Eigenvalues
- Singular Vectors for 2 by 2 Matrices
- The First Singular Vectors $v_1$
- Computing Eigenvalues and Sigular Values
7.2 Image Processing by Linear Algebra
- Sigular Values with Diagonals
- Image Compression by the SVD
7.3 Pricipal Component Analysis(PCA by the SVD)
- Norm of a Matrix
- The Eckart-Young Theorem
- Principal Component Analysis
- The Geometry Behind PCA
- The Geomeric Meaning of Eckart-Yound
- The Statistics Behind PCA
- The Linear Algegra Behind PCA
特異値分解に関していうと5版が一番充実しているようです。
以下は6版の簡易翻訳です。DeepLにより翻訳したものを若干修正しています。
7 特異値分解(SVD)
7.1 特異値・特異ベクトル
7.2 線型代数による画像処理
7.3 主成分分析(SVDによるPCA)
この章では、一つの考え方を展開します。その考え方は、あらゆる正方行列や矩形行列に適用されます。それは固有ベクトルの拡張です。しかし、そのためには2組の正規直交ベクトルが必要です。入力ベクトルの$v_1$ から $v_n$ と出力ベクトルの $u_1$ から $u_m$ です。これは、$m$ x $n$の行列としては自然なことです。ベクトル$v_1$〜$v_r$は行空間の基底であり、$u_1$〜$u_r$は列空間の基底です。そして、$r=rank(A)$であればランク1の$r$個の要素と対角行列$\sigma$の正の特異値$\sigma_1 \ge \sigma_2 \ge \cdots \ge \sigma_r>0$ から$A$を復元できます。
右特異ベクトルは$A^TA$の固有ベクトルです。これらは$A$の行空間と零空間の基底を与えます。左特異ベクトル$u_i$は$AA^T$の固有ベクトルです。これらは$A$の列空間と左零空間の基底を与えます。このとき、$Av_i$は$i \le r$に対して$\sigma_iu_i$に等しくなります。行列$A$は2つの直交基底で対角化されます:$AV=U\Sigma$。
なお、$U \Sigma$の非零列は$\sigma_1u_1\le \cdots\le \sigma_r u_r$です。とすると、上の箱の$U\Sigma$と$V^T$の積は、列×行の積です。これは対称行列$S$における$S=Q\Lambda Q^T$と関連します。
$A$が対称正定値行列$S$であるときは各$u_i=v_i$です。それらの特異ベクトルは固有ベクトル$q_i$となります。そして、特異値$\sigma_i$は$S$の固有値となります。$A$が正方形でない場合や対称でない場合は、$S=Q\Lambda Q^T$の代わりに$A=U\Sigma V^T$が必要です。
図7.1では、$x$→$V^Tx$→$U \Sigma V^Tx=Ax$の各ステップが、単位ベクトル$x$の円に対してどのように作用するかを示しています。これらは、円をベクトル$Ax$の楕円に引き伸ばしています。
SVDは、データ行列を理解するための貴重な方法です。この場合、中心化されたデータの$AA^T$を、$n-1$で割ったものは標本共分散行列です(7.3節)。その固有値は$\sigma_1^2$から$\sigma_r^2$です。
その固有ベクトルはSVDの$u$です。主成分分析(PCA)は、データ行列$A$の特異ベクトルに基づいているといえます。
SVDは、写真=ピクセルの行列をそのランク1の成分に分解することで、素晴らしい画質を可能にします。1つの$\sigma_iu_iv_i^T$を増やすたびに、写真がより鮮明になります。7.2節では、その例と優れたウェブサイトへのリンクを示します。7.3節では、PCAと統計学の分散共分散行列との関連について説明します。
7.1 特異値と特異ベクトル
-
行列の特異値分解は $A=U\Sigma V^T$ または $AV=\Sigma U$ です。
-
$Av_i=\sigma_iu_i$ の特異ベクトル $v_i$,$u_i$ は、$V^TV=I$, $U^TU=I$ という直交性を持ちます。
-
対角行列$\Sigma$は特異値$\sigma_1 \ge \sigma_2 \ge \cdots \ge \sigma_r>0$ を含みます。
-
それらの特異値の2乗$\sigma_i^2$は$A^TA$と$AA^T$の固有値$\lambda_i$です。
対称行列の固有ベクトルは直交しています。直交性を放棄することなく、対称行列を越えてすべての行列に適用するために、$m$ x $n$行列ごとに、$R^n$の$n$個の正規直交ベクトル$v_1, \cdots,v_n$ の組と$R^m$の第2の正規直交ベクトル$u_1,\cdots,u_m$の組が必要です。$Sx=\lambda x$の代わりに、$Av=\sigma u$が必要です。
つぎの非対称行列$A$は直交入力$v_1,v_2=(1,1)$と$(-1,1)$を持ちます。
出力(9,3)と(-1,3)も直交しています!これらの$v$と$u$は単位ベクトルではありませんが、それは簡単に直せます。(1,1)と(-1,1)は、$\sqrt{2}$で割る必要があります。(3,1)と(-1,3)は$\sqrt{10}$で割って$u_1$と$u_2$とする必要があります。特異値$\sigma_1,\sigma_2$は$3\sqrt{5}$と$\sqrt{5}$です。
この2つのベクトルからなる2つの式は1つの行列式$AV=U\Sigma$とすることができます。$V$には入力$v_1$と$v_2$が入ります。$\frac{\sqrt{5}}{\sqrt{10}}=\frac{1}{2}$のとき、出力$\sigma_1u_1$と$\sigma_2 u_2$は$U\Sigma$にあります。
$V$と$U$は直交行列です!$AV=U\Sigma$に$V^T$を掛けると、$A$となります。
$AV=U \Sigma$は、$A=U\Sigma V^T$になります。これは、$A=\sigma_1 u_1 v_1^T + \sigma_2 u_2 v_2^T$に分解されます。
このSVDの式は、直交する$v$と$u$の求め方以外はすべてを語っています。
すべての行列 $A$ は、1組の固有ベクトルではなく、2組の特異値ベクトルによって対角化されます。
この2×2の例では、$\sigma_1=3\sqrt{5}$が$\sigma_2=\sqrt{5}$より大きいので、最初の部分が2番目より重要です。$A$を得るには、$\sigma_1u_1v_1^T+\sigma_2u_2v_2^T$というように部分を足します:
import numpy as np
from numpy.linalg import svd, matrix_rank
np.set_printoptions(precision=2)
np.set_printoptions(suppress=True) #suppressは禁止の意味
A = np.array([[5, 4], [0, 3]])
print('matrix A\n', A)
print('rank: ', matrix_rank(A))
# 特異値分解
u, s, vh = svd(A)
print('特異値:', s)
sigma1=3*np.sqrt(5)
sigma2=np.sqrt(5)
print('3・sqrt(5)=',sigma1.round(2),'sqrt(5)=',sigma2.round(2))
#復元
A_recover = (u @ np.diag(s) @ vh)
print('\n recover A:\n', A_recover)
A=\left[\begin{array}{c,c}
1,0\\
1,1\\
1,2
\end{array}\right]\\
A^TA=\left[\begin{array}{c,c,c}
1,1,1 \\
0,1,2
\end{array}\right]
\left[\begin{array}{c,c}
1,0\\
1,1\\
1,2
\end{array}\right]=
\left[\begin{array}{c,c}
1\times 1+1\times 1+1\times 1,1\times 0+1\times 1+1\times 2 \\
0\times 1+1\times 1+2\times 1,0\times 0+1\times 1+2\times 2
\end{array}\right]=
\left[\begin{array}{c,c}
3,3 \\
3,5
\end{array}\right]\\
AA^T=\left[\begin{array}{c,c}
1,0\\
1,1\\
1,2
\end{array}\right]
\left[\begin{array}{c,c,c}
1,1,1 \\
0,1,2
\end{array}\right]=
\left[\begin{array}{c,c,c}
1\times 1+0\times0, 1\times 1+0\times 1,1\times 1+0\times2 \\
1\times 1+1\times 0,1\times 1+1\times 1,1\times 1+1 \times 2 \\
1\times 1+2\times 0,1\times 1+2\times 1,1\times 1+2 \times 2
\end{array}\right]=
\left[\begin{array}{c,c,c}
1, 1, 1 \\
1, 2, 3 \\
1, 3, 5
\end{array}\right]
A = np.array([[1, 0], [1, 1],[1,2]])
A,np.transpose(A)@A,A@np.transpose(A)
SVDの幾何学
SVDは、行列を$A=U\Sigma V^T$:(直交行列)x(対角行列)x(直交行列) に分解します。2次元を用いて、それらの役割の推移を描くことができます。直交行列$U$と$V$は平面を回転させます。対角行列$\Sigma$は、軸に沿って平面を引き伸ばします。図7.1は、回転と引き伸ばしと回転を表しています。
円上のベクトル$v$は、楕円上では$Av=\sigma u$になります。
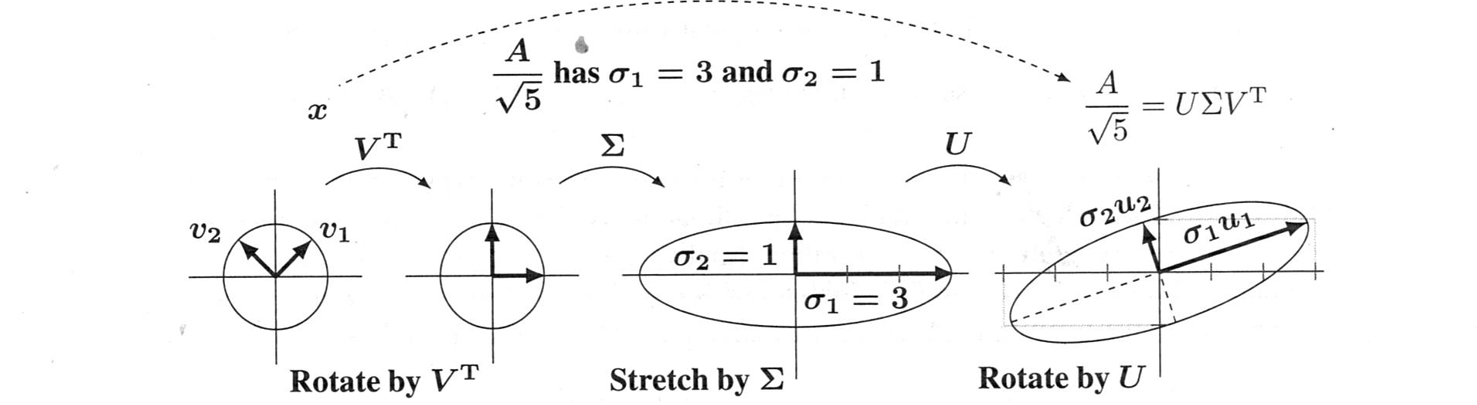
図7.1: $U$と$V$は回転と鏡映の可能性があります。$\Sigma$は円を楕円に引き伸ばします。
この図は、$\sigma_1>0$と$\sigma_2>0$の2×2可逆行列に適用されます。まず、任意の$x$を$V^Tx$に回転させます。次に、$\Sigma$はそのベクトルを$\Sigma V^Tx$に引き伸ばします。次に$U$は$U\Sigma V^Tx$に回転します。鏡に映った見え方とならないために、すべての行列式を正にしています。行列の4つの数字$a,b,c,d$は、2つの回転角$\theta, \phi$と$\Sigma$の2つの数字$\sigma_1, \sigma_2$につながります。
問題1 行列が対称であれば、$b=c$です。今、$A$は3(4ではない)個のパラメータを持っています。
対称行列の場合、$\theta,\phi,\sigma_1,\sigma_2$の4つはどのようにして3つの数値になるのでしょうか?
問題2 $\theta=30^o$, $\sigma_1=2$, $\sigma_2=1$, $\phi=60^o$のとき、$A$はいくらでしょうか。$\det=2$ を確認します。
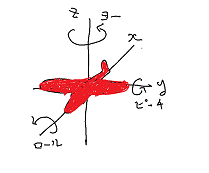
問題3 $A$が3×3(9パラメータ)の場合、$\Sigma$は3つの特異値を持ちます。
$U$と$V$はそれぞれ3回転して3十3十3=9個になります。パイロットにとってのこの3つの回転は何でしょうか?
解答 飛行機は「ピッチ」と「ロール」、そして「ヨー」ができます。(Wolfram EulerAnglesを参照)。
問題4 $S=QAQ^T$が対称正定値であるとき、そのSVDは何でしょうか?
解答 SVDはちょうど$U\Sigma V^T=QAQ^T$です。行列$U=V=Q$は直交しています。
また、対角固有値行列$A$は特異値行列$\Sigma$となります。
問題5 $S=QAQ^T$が負の固有値($Sx=-\alpha x$)を持つ場合、特異値$\sigma$と、ベクトル$v$、$u$は何でしょうか。
解答 特異値は$\sigma=+\alpha$(正)となります。
特異ベクトル($u$か$v$のどちらか)は必ず$-x$(符号を逆にする)です。
すると、$Sx=-\alpha x$は$SV=\sigma u$と同じになります。
2つの符号の変化はキャンセルされます。
xx=np.random.rand(10000,2)*2-1
fig = plt.figure(figsize = (3, 3))
plt.scatter(np.transpose(xx)[0],np.transpose(xx)[1],s=1)
plt.show()
A = np.array([[5, 4], [0, 3]])
print('matrix A\n', A)
print('rank: ', matrix_rank(A))
# 特異値分解
u, s, vh = svd(A)
print('u\n',u)
print('特異値:', s)
print('vh\n',vh)
fig = plt.figure(figsize = (3, 3))
b=[]
b2=[]
for x1,x2 in zip(np.transpose(xx)[0],np.transpose(xx)[1]):
b0=(vh@np.array([x1,x2]))[0]
b1=(vh@np.array([x1,x2]))[1]
b.append([b0,b1])
b=np.array(b)
plt.scatter(b[:,0],b[:,1],s=1)
plt.show()
fig = plt.figure(figsize = (3, 3))
b=[]
b2=[]
for x1,x2 in zip(np.transpose(xx)[0],np.transpose(xx)[1]):
b0=(u@np.diag(s)@vh@np.array([x1,x2]))[0]
b1=(u@np.diag(s)@vh@np.array([x1,x2]))[1]
b.append([b0,b1])
b=np.array(b)
plt.scatter(b[:,0],b[:,1],s=1)
plt.show()
fig = plt.figure(figsize = (3, 3))
xx=np.random.rand(10000,2)*2-1
b=[]
b2=[]
for x1,x2 in zip(np.transpose(xx)[0],np.transpose(xx)[1]):
b0=(A@np.array([x1,x2]))[0]
b1=(A@np.array([x1,x2]))[1]
b.append([b0,b1])
b=np.array(b)
plt.scatter(b[:,0],b[:,1],s=1,c='r')
plt.show()
完全形(full size)SVD
完全形には、$A$と$A^T$の零空間の基底ベクトルが含まれています。それらのベクトル$v_{r+1}$〜$v_n$と$u_{r+1}$〜$u_m$は直交行列$V$($n$×$n$)と$U$($m$×$m$)を完成します。すると、行列$\Sigma$は$A$と同じに($m$×$n$)なります。ただし、その主対角線上にある$r$個の特異値$\sigma_1,\sigma_2 \ge \cdots \ge \sigma_r>0$を除いて、$\Sigma$はすべてゼロです。これらの$\sigma$はベクトル$u_1$〜$u_r$を乗算します。
ss=np.diag(s)
s,ss,u,u@ss,A@vh.T
$V^T=V^{-1}$ を右に掛けると、この式 $AV=U \Sigma$ は特異値分解の最も有名な形 $A=U\Sigma V^T$ となります。行列$V$と$U$は正方形で、行空間十零空間、列空間十$N(A^T)$の基底を持ちます。
簡約SVD
$A$のランクが小さく、零空間が大きいとき、完全形$AV=U \Sigma$は、$\Sigma$にたくさんのゼロを持ちます。これらのゼロは行列の乗算には何の役にも立ちません。
SVDの肝は、$v$と$u$と$\sigma$の最初の$r$にあります。確実に0が出る部分を取り除くことで、$AV=U \Sigma$を$AV_r=U_r \Sigma_r$にすることができます。これで、$\Sigma_r$が正方形になる簡約SVDは$(m \times n)(n \times r)=(m \times r)(r \times r)$となります。
$V_r^TV_r=I_r$と$U_r^TU_r=I_r$は、これらの直交する単位ベクトル$v$と$u$から常に得られます。
$V_r$と$U_r$が正方形でないときは、$V_r V_r^T \ne I$と$U_rU_r^T \ne I$の完全逆行列は成り立たちません。しかし、$A=U_r\Sigma_r V_r^T=u_1 \sigma_1 v_1^T+\cdots+u_r\sigma_rv_r^T$は真です。この簡約形の方が好ましい形です。完全形の$A=U\Sigma V^T$ では他の乗算はゼロしか与えられないからです。
例1 2×2の行列は$r=m=n$です。簡約形は完全形です。
例2 $A=[122]=[1][3][122]/3=U_r\Sigma_rV_r^T$ は $r=1$ と $\sigma_1=3$ です。
残りの$U\Sigma V^T$は、$\Sigma$に0が多いので、$A$には何も貢献しません。
$A$を$\sigma_1u_1v_1^T+\cdots+\sigma_ru_rv_r^T$に分離する鍵は、$\sigma_1u_1v_1^T$で停止することです。なぜならランクが1だからです。
SVDの証明
目的は$A=U\Sigma V^T$となる特異ベクトル$u$と$v$の2組を特定することです。この特異ベクトルを見つけるには、対称行列$A^TA$と$AA^T$を作るのが一つの方法です。
(8)、(9)ともに対称行列を生成します。通常、$A^TA$と$AA^T$は異なります。右辺はどちらも特殊な形$Q \Lambda Q^T$を持ちます。$A^TA$と$AA^T$の固有ベクトルは、$V$と$U$の特異ベクトルです。つまり、(8)と(9)から、$A=U\Sigma V^T$の3つの部分が、それらの対称行列$A^TA$と$AA^T$にどうつながるかがわかります。
$V$は$A^TA$の正規直交固有ベクトルを含みます。
$U$には$AA^T$の正規直交固有ベクトルが含まれます。
$\sigma_1^2$〜$\sigma_r^2$は$A^TA$と$AA^T$の両方の非零固有値です。
よってまだ終わりではありません。SVDでは、$Av_k=\sigma_ku_k$が必要です。これは、各右特異ベクトル$v_k$を左特異ベクトル$u_k, k=1,\cdots,r$と結合します。$v$を選ぶと、その選び方で$u$の符号が決まります。$Su=\lambda u$なら、$S(-u)=\lambda(-u)$でもあり、選ぶべき符号を知らなければなりません。それ以上に、以下のようなものがあります。$\lambda$が二重固有値のとき、固有ベクトルの平面は全体となります。その平面で$v$を2つ選ぶと、$Av=\sigma u$で両方の$u$がわかります。
計画では、まず$v$のほうから始めます。$A^TA$の直交固有ベクトル$v_1,\cdots,v_r$を選びます。
そして、$\sigma_k=\sqrt{\lambda_k}$を選びます。$u$を決定するためには、$Av=\sigma u$であることが必要です:
これでSVDが出来上がります!これらのベクトル$u_1$〜$u_r$が$AA^T$の固有ベクトルであることを確認してみます。
$v$の方は正則になるように選ばれています。$u$のものも正規直交であることを確認しなければなりません:
$(AA^T)A=A(A^TA)$が式(11)の鍵であることに注目してください。この法則 $(AB)C=A(BC)$ は、線形代数学の非常に多くの証明の鍵です。この括弧を移動させるのは強力なアイデアです。結合法則が許されます。これで証明は完成です。
print("$V$は$A^TA$の正規直交固有ベクトルを含みます。")
print(vh.T)
sss,vvv=np.linalg.eig(A.T@A)
print(sss)
print(vvv)
print("$U$には$AA^T$の正規直交固有ベクトルが含まれます。")
print(u)
sss,vvv=np.linalg.eig(A@A.T)
print(sss)
print(vvv)
例題1(これで完成)元
A=\left[\begin{array}{c c} 5 & 4 \\ 0 & 3 \end{array} \right]
についてUと$\Sigma$と$V$を求めよ。
ランク2であるこの$A$は、2つの正の特異値$\sigma_1$と$\sigma_2$を持ちます。このとき、$\sigma_1$は$\lambda_{max}=5$より大きく、$\sigma_2$は$\lambda_{min}=3$より小さいことを確認します。$A^TA$と$AA^T$で始めます。
これらは同じトレース$\lambda_1+\lambda_2=50$、同じ固有値$\lambda_1=\sigma_1^2=45$、$\lambda_2=\sigma_2^2=5$です。平方根は $\sigma_1=3\sqrt{45}=3\sqrt{5}$, $\sigma_2=\sqrt{5}$です。すると、$\sigma_1$×$\sigma_2$は15になり、これが$A$の行列式となります。
次に、$V$を求めます。$V$の鍵は$A^TA$の固有ベクトル(固有値45と5)を見つけることです:
このとき、$v_1$と$v_2$は長さ1に再スケーリングした直交固有ベクトルです。$\sqrt{2}$で割ると、
右の特異ベクトル $v_1=\frac{1}{\sqrt{2}}\left[\begin{array}{c} 1 \ 1 \end{array} \right]$ と $v_2=\frac{1}{\sqrt{2}}\left[\begin{array}{c} -1 \ 1 \end{array} \right]$ (予測通り)となります。
左の特異ベクトルは$u_1=Av_1/\sigma_1$、$u_2=Av_2/\sigma_2$です。$v_1$,$v_2$ を $A$ で掛け合わせればよい:
$\sqrt{10}$で割ると、$u_1$と$u_2$は単位ベクトルになります。すると、予想通り$\sigma_1=\sqrt{45}$、$\sigma_2=\sqrt{5}$となります。$A$の特異値分解は$U$×$\Sigma$×$V^T$です($V$ではありません)。
最後に最後の$n-r$個のベクトル、$v_{r+1}$〜$v_n$と最後の$m-r$個のベクトル、$u_{r+1}$〜$u_m$を選ぶ必要があります。これは簡単です。これらの$v$と$u$は、$A$と$A^T$の零空間にあります。これらの零空間には、任意の正規基底を選ぶことができます。それらは自動的に、$A$の行空間の最初の$v$と列空間の最初の$u$に直交することになります。これは空間全体が直交しているからです。
$N(A)\perp C(A^T)$ と $N(A^T)\perp C(A)$。SVDの証明は、あの線形代数の基本定理で完結します。
もう一度言うと: 良いコードは$A^TA$と$AA^T$から始まりません。その代わりに、まず、2本の対角線だけを残す回転で$A$にゼロを作ります($\sigma$に影響を与えません)。このセクションの最後のページでは、SVDの計算を成功させる方法について説明します。これで、式(1)の完全形SVDの$U$と$V$と$\Sigma$: $m\textbf{u}$のものと$n\textbf{v}$'sのものが揃いました。
$A^TA$の固有値が$\Sigma^T\Sigma$にあり、同じ数$\sigma_1^2$〜$\sigma_r^2$が$AA^T$の固有値として$\Sigma^T\Sigma$にあることにお気づきでしょうか?驚くべき事実として、$BA$は常に$AB$と同じ非零固有値を持っています。$BA$は$n$×$n$で、$AB$は$m$×$m$です。
ABとBA:等しい非ゼロ固有値
$A$が$m$×$n$、$B$が$n$×$m$のとき、$AB$と$BA$の非ゼロ固有値は同じです。
$ABx=\lambda x$、$\lambda \ne 0$で始めます。両辺に$B$をかけると、$BABx=\lambda Bx$となります。これは、$Bx$が$BA$の固有ベクトルで、同じ特異値$\lambda$を持つことを意味し、まさに我々が望んでいたことです。$Bx$が本当に$BA$の非ゼロ固有ベクトルであることを確認するために、$\lambda \ne 0$が必要です。$B$が正方形で反転可能なら、$B^{-1}(BA)B=AB$となることに注意します。これは、$BA$が$AB$と似ています:同じ固有値であることを意味しています。しかし、最初の証明では、$A$と$B$が$m$×$n$と$n$×$m$であることを認めています。これは、$B=A^T$のときのSVDの重要な例をカバーしています。その場合、$A^TA$と$AA^T$はともに$A$の$r$個の非ゼロ特異値を導きます。
$m$が$n$より大きければ、$AB$は$BA$に比べて$m$-$n$余分にゼロの固有値を持つことになります。
2×2 行列の特異ベクトル
ここでは、2×2 SVDの証明を画像で紹介します。$Av$と$Aw$も垂直になるように、垂直なベクトル$v$と$w$を探します。最初の推測では $V=(1,0)$, $W=(0,1)$ です。$AV$から$AW$までの角度$\theta$が小さすぎます(第1図では$90^o$以下)。また、$AW$と$AV$の間の角度180ー$\theta$は大きすぎます(第2図では$90^o$以上)。したがって、$V$と$W$の間にはちょうどよい$v$があるはずです。
$Av$から$Aw$までの角度はちょうど$90^o$であり、SVDが証明されます:直交入力 $v\perp w$ 、直交出力 $Av \perp Aw$ です。
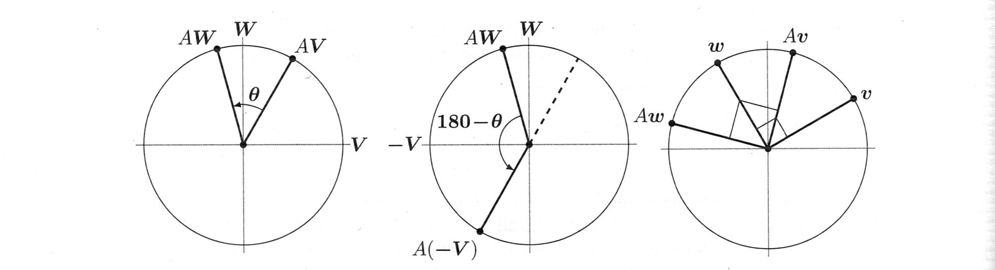
図7.2: $AV$から$AW$までの角度$\theta$は$90^。$。$AW$から$AV$までの角度180一$\theta$。
その中間で、$v$が$V$から$W$に向かうとき、$Av$から$Aw$への角度はちょうど$90^o$になります。図ではベクトルの長さを示していません。
項「第一特異ベクトル$v_1$について」以降では、$v_1$の新しい見方を確立します。
いままでは、$v$を$A^TA$の固有ベクトルとしました。確かにその通りです。
しかし、この特異ベクトルを一度に理解するのではなく、1つずつ理解する方法があるのです。
第一特異ベクトルv1について
比$\frac{| Ax|}{| x||}$を最大化します。ベクトル$x=v_1$で最大となるのは$\sigma_1$です。(14)
図7.1の楕円は、最大になる$x$が$v_1$である理由を示したものです。$v_1$を横にたどっていくと、$Av_1=\sigma_1u_1$で終わります。楕円の長軸は長さ$|Av_1|=\sigma_1$です。
しかし、SVDの独立したアプローチを目指しています!$U$や$\Sigma$や$V$を既に知っていることを前提にしているわけではありません。$x=v_1$のとき、比$\frac{|ax|}{|x|}$が最大であることをどう認識するか?簡単な方法としては、関数を2乗して$S=A^TA$を解くことです。
問題:$\frac{|Ax|^2}{|x|^2}=\frac{x^TA^TAx}{x^Tx}=\frac{x^TSx}{x^Tx}$の最大値$\lambda$を求めよ。---- (15)
この「レイリー商」を最大化するには、任意の$x$を$c_1x+\cdots+c_nx_n$として$Sx_i=\lambda_i x_i$で書きます。
$$\frac{s^TSx}{x^Tx}=\frac{c_1^2\lambda_1+\cdots+c_n^2\lambda_n}{c_1^2+\cdots+c_n^2} \le \lambda_1=Sの最大固有値$$
とすると、(15)の比率を最大にするのに最適なものは$S$の固有ベクトルです!
完全なSVDを行うには、すべての特異ベクトルと特異値が必要です。$v_2$と$\sigma_2$を求めるには、$v_1$に直交するベクトル$x$だけを見るように最大問題を調整します。
$v_1^Tx=0$の条件下で$\frac{|Ax|}{|x|}$を最大化: 最大値は$x=v_2$で$\sigma_2$です。
"ラグランジュ乗数 "は、$v_1^Tx=0$のような$x$に対する制約を扱うために発明されたものです。
すべての特異ベクトル$v_{k+1}$は、最初の$v_1,\cdots,v_k$に垂直なすべてのベクトルに対して、最大比$|Ax|/|x|$を与えます。楕円体の軸と対称行列$A^TA$や$AA^T$の固有ベクトルを、一度に、あるいは別々に求めているのです。
質問:正方行列$A$の固有値がすべて$\sigma_1$以下となるのはなぜか?
解答: 対角行列 $U$ と $V^T$ を掛け合わせても、ベクトルの長さは変わりません:
固有ベクトルは$|Ax|=|\lambda||x|$となります。
とすると、(17)は、$|\lambda||x|\le \sigma_1|x|$ と$|\lambda| \le \sigma_1$を与えます。
質問: $A=xy^T$がランク1であるとき、$u_1$と$v_1$と$\sigma_1$は何ですか?$|\lambda_1| \le \sigma_1$を調べてみましょう。
解答: 特異ベクトル $u_1=x/|x|$ と $v_1=y/|y|$ は長さ1です。
このとき、特異値行列$\Sigma$の中で唯一0でない数は$\sigma_1=|x||y|$です。
以下はSVDです。
観察 $A=xy^T$ の非ゼロ固有値は $\lambda_1=y^Tx$ だけです。固有ベクトルは $Ax=(xy^T)x=x(y^Tx)=\lambda_1x$ だからです。すると、不等式 $|\lambda_1| \le \sigma_1$ は次のようになります。まさにSchwarzの不等式 $|y^Tx| \le |x||y|$です。
固有値と特異値を計算する
対称固有値問題の主な違いはなにか?$Sx=\lambda x$ と $Av=\sigma u$ の違いは?
$\lambda$'sと$\sigma$'sを計算する前に、$S$と$A$をどこまで簡略化できるのだろうか。
$Q$が直交するとき、$S$と$Q^{-1}SQ=Q^TSQ$で固有値が同じになります。
だから、$Q^{-1}SQ=Q^TSQ$にゼロを作る自由度は限られています(対称のままである)。$Q^{-1}S$でゼロを作りすぎると、最後の$Q$で壊されてしまいます。良い$Q^{-1}SQ$は三角錐になります:$S$を3つの非ゼロの対角線に減らすことができます。
$Q_1$が$Q_2$と異なっていても、$A$と$Q_1^{-1}AQ_2$では特異値が同じになります。
$Q_1^{-1}AQ_2$の方がゼロを作る自由度が高くなります。正しい$Q$を使えば、これは2角形になります(2つの非ゼロの対角線)。となるように、$Q$と$Q_1$と$Q_2$をすぐに求めることができます。
すでに$A$の特異値が、$S=A^TA$の固有値の平方根であることを知っているはずです。$S=A^TA$の固有値です。そして、$Q_1^{-1}AQ_2$の特異値は、$A$の特異値と同じです。(双対角)$^T$(双対角)を掛け合わせると、三角錐が見えます。
これは、取ってはいけない選択肢を提示しています。$A^TA$を掛けてその固有値を求めるのはやめましょう。これは無駄な作業であり、問題の条件が不必要に2乗されることになります。SVDのGolub-Kahanアルゴリズムは、$A$に対して直接、2つのステップで動作します:
-
(19)のように$A^*=Q_1^{-1}AQ_2$が二角形になるように$Q_1$と$Q_2$を求めます:同じ$\sigma$を使います
-
$A^*$の特異値を保存するように、シフト$QR$アルゴリズム(6.5節、284ページ)を調整します。
ステップ1では、$m$ x $n$の行列$A$を双対角形にするために$O(mn^2)$回の乗算が必要です。そうすると、後のステップでは、二角形の行列でのみ動作することになります。通常、特異値を求めるには$O(n^2)$回の乗算が必要です(ほぼ機械精度に近い精度)。完全なアルゴリズムはGolub-Van Loanの第4版の489〜492ページに記載されています: 聖書
$A$が本当に大きいときは、ランダムサンプリングに頼ることになります。
非常に高い確率で、ランダム化線形代数は正確な結果を与えます。ギャンブラーは、注意深いランダムサンプリングにより確実に良い結果が得られると言うことでしょう。
Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。