LoginSignup
3
1

More than 5 years have passed since last update.

@inashiro

Python からLarch を利用してXAFS 解析3 - EXAFS フィッティング

Last updated at Posted at 2018-04-01

概要

本記事は以下の記事の続編です。

Python からLarch を利用してXAFS 解析
https://qiita.com/inashiro/items/f1c10440618cf73a2d81
Python からLarch を利用してXAFS 解析2 - X線データベース機能の利用
https://qiita.com/inashiro/items/04bedefa2a560ffa666d

EXAFS の解析には、多重散乱理論によるシミュレーションが可能なFEFF 1というプログラムが利用されています。例えば、広く利用されているXAFS のGUI 解析環境であるDemeter パッケージにはFEFF6 の簡易版がバンドルされており、EXAFS スペクトルのシミュレーションやフィッティングが可能です。2

Demeter(ATHENA やARTEMIS) のバックエンドライブラリであるLarch でも、FEFF を操作したり、FEFF で計算した散乱パスを読み込んでEXAFS スペクトルを計算・フィッティングすることが可能です。しかし、FEFF を操作する部分はPython からは使いにくく、未だ発展途上のようです。3 なので、現状ではFEFF で計算した散乱パスを別途用意して、Larch で読み込むという方法を取るのが良いでしょう。あまりスマートではないですが、ARTEMIS よりもパラメータを詳細に振った解析がしやすく、また大量のデータに対する自動フィッティング（いわゆるin situ/operando 解析）には威力を発揮します。

この記事では、Larch でFEFF の散乱パスを読み込みEXAFS 解析に利用する方法を紹介します。具体的には、以前の記事4で扱ったCu 箔のデータに対して、フィッティング解析を行います。

実行環境はJupyter Notebook を想定しており、ライブラリの読み込み等は順序含めて以下の通りとします。

In[1]
from larch import Interpreter
import larch_plugins as lp
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm

session = Interpreter()
%matplotlib inline

実験結果の処理（Cu 箔）

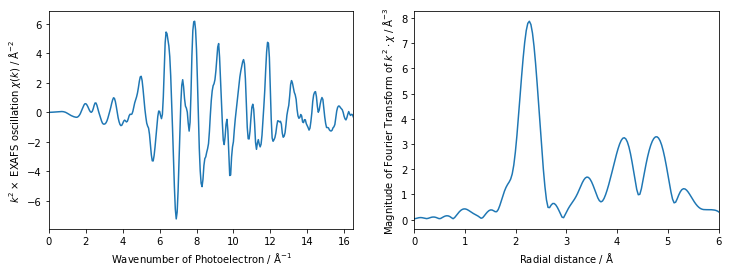
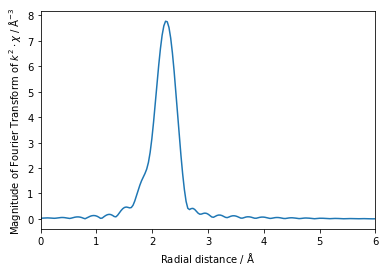
データの処理（バックグラウンド除去・EXAFS振動の抽出・動径構造関数の導出）条件は以下の通りとします。

In[2]
# loading data
Cu_expt = lp.io.read_ascii("./K_Cu12.5K_Si111_20101108.txt", labels="energy mu", _larch=session)
# calc exafs spectrum
lp.xafs.autobk(Cu_expt, kmin=0.0, kmax=16.5, rbkg=1.0, group=Cu_expt, _larch=session)
# fourier transformation
lp.xafs.xftf(Cu_expt, kweight=2, kmin=3, kmax=15.0, window="hanning", dk=1.0, group=Cu_expt, _larch=session)

# Plot
fig = plt.figure(figsize=(12, 4))
ax1 = fig.add_subplot(121)
ax1.plot(Cu_expt.k, Cu_expt.k**2 * Cu_expt.chi)
ax1.set_xlim(0, Cu_expt.k.max())
ax1.set_xlabel("Wavenumber of Photoelectron / $\mathrm{\AA}^{-1}$")
ax1.set_ylabel("$k^2 \\times$ EXAFS oscillation $\chi (k)$ / $\mathrm{\AA}^{-2}$")
ax2 = fig.add_subplot(122)
ax2.plot(Cu_expt.r, Cu_expt.chir_mag)
ax2.set_xlim(0, 6)
ax2.set_xlabel("Radial distance / $\mathrm{\AA}$")
ax2.set_ylabel("Magnitude of Fourier Transform of $k^2 \cdot \chi$ / $\mathrm{\AA}^{-3}$")
plt.show()

output_6_0.png

FEFF による散乱パスの計算

feff.inp の作成

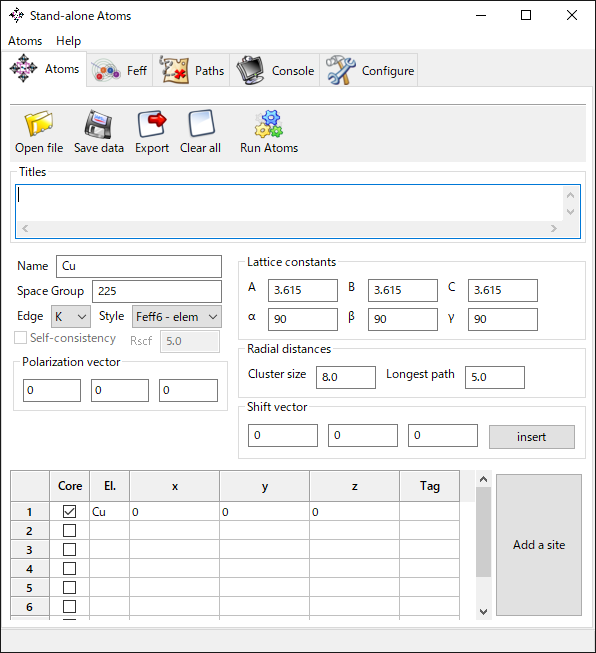
FEFF を使って散乱パスを計算します。FEFF の計算には、feff.inp という入力ファイルが必要です。しかし、feff.inp には計算に用いるクラスターの原子座標をすべて指定する必要があり、手で計算・入力するのは現実的ではありません。恐らく現状では、Demeter パッケージに入っているStand Alone Atoms を使うのが、最も容易にfeff.inp を作成する方法でしょう。

今回は、Stand Alone Atoms を用いて、以下の図の通り入力した構造でfeff.inp を作成しました。

perl_2018-04-01_16-54-44.png

作成したfeff.inp を以下に示します。（ちょっと長いです。）

feff.inp
 HOLE      1   1.0

 CONTROL   1      1     1     1

 PRINT     1      0     0     0

 RMAX      6

 POTENTIALS
     0     29     Cu        
     1     29     Cu        

 ATOMS
    0.00000    0.00000    0.00000  0  Cu            0.00000
    1.80750    1.80750    0.00000  1  Cu.1          2.55619
   -1.80750    1.80750    0.00000  1  Cu.1          2.55619
    1.80750   -1.80750    0.00000  1  Cu.1          2.55619
   -1.80750   -1.80750    0.00000  1  Cu.1          2.55619
    1.80750    0.00000    1.80750  1  Cu.1          2.55619
   -1.80750    0.00000    1.80750  1  Cu.1          2.55619
    0.00000    1.80750    1.80750  1  Cu.1          2.55619
    0.00000   -1.80750    1.80750  1  Cu.1          2.55619
    1.80750    0.00000   -1.80750  1  Cu.1          2.55619
   -1.80750    0.00000   -1.80750  1  Cu.1          2.55619
    0.00000    1.80750   -1.80750  1  Cu.1          2.55619
    0.00000   -1.80750   -1.80750  1  Cu.1          2.55619
    3.61500    0.00000    0.00000  1  Cu.2          3.61500
   -3.61500    0.00000    0.00000  1  Cu.2          3.61500
    0.00000    3.61500    0.00000  1  Cu.2          3.61500
    0.00000   -3.61500    0.00000  1  Cu.2          3.61500
    0.00000    0.00000    3.61500  1  Cu.2          3.61500
    0.00000    0.00000   -3.61500  1  Cu.2          3.61500
    3.61500    1.80750    1.80750  1  Cu.3          4.42745
   -3.61500    1.80750    1.80750  1  Cu.3          4.42745
    1.80750    3.61500    1.80750  1  Cu.3          4.42745
   -1.80750    3.61500    1.80750  1  Cu.3          4.42745
    3.61500   -1.80750    1.80750  1  Cu.3          4.42745
   -3.61500   -1.80750    1.80750  1  Cu.3          4.42745
    1.80750   -3.61500    1.80750  1  Cu.3          4.42745
   -1.80750   -3.61500    1.80750  1  Cu.3          4.42745
    1.80750    1.80750    3.61500  1  Cu.3          4.42745
   -1.80750    1.80750    3.61500  1  Cu.3          4.42745
    1.80750   -1.80750    3.61500  1  Cu.3          4.42745
   -1.80750   -1.80750    3.61500  1  Cu.3          4.42745
    3.61500    1.80750   -1.80750  1  Cu.3          4.42745
   -3.61500    1.80750   -1.80750  1  Cu.3          4.42745
    1.80750    3.61500   -1.80750  1  Cu.3          4.42745
   -1.80750    3.61500   -1.80750  1  Cu.3          4.42745
    3.61500   -1.80750   -1.80750  1  Cu.3          4.42745
   -3.61500   -1.80750   -1.80750  1  Cu.3          4.42745
    1.80750   -3.61500   -1.80750  1  Cu.3          4.42745
   -1.80750   -3.61500   -1.80750  1  Cu.3          4.42745
    1.80750    1.80750   -3.61500  1  Cu.3          4.42745
   -1.80750    1.80750   -3.61500  1  Cu.3          4.42745
    1.80750   -1.80750   -3.61500  1  Cu.3          4.42745
   -1.80750   -1.80750   -3.61500  1  Cu.3          4.42745
    3.61500    3.61500    0.00000  1  Cu.4          5.11238
   -3.61500    3.61500    0.00000  1  Cu.4          5.11238
    3.61500   -3.61500    0.00000  1  Cu.4          5.11238
   -3.61500   -3.61500    0.00000  1  Cu.4          5.11238
    3.61500    0.00000    3.61500  1  Cu.4          5.11238
   -3.61500    0.00000    3.61500  1  Cu.4          5.11238
    0.00000    3.61500    3.61500  1  Cu.4          5.11238
    0.00000   -3.61500    3.61500  1  Cu.4          5.11238
    3.61500    0.00000   -3.61500  1  Cu.4          5.11238
   -3.61500    0.00000   -3.61500  1  Cu.4          5.11238
    0.00000    3.61500   -3.61500  1  Cu.4          5.11238
    0.00000   -3.61500   -3.61500  1  Cu.4          5.11238
    5.42250    1.80750    0.00000  1  Cu.5          5.71582
   -5.42250    1.80750    0.00000  1  Cu.5          5.71582
    1.80750    5.42250    0.00000  1  Cu.5          5.71582
   -1.80750    5.42250    0.00000  1  Cu.5          5.71582
    5.42250   -1.80750    0.00000  1  Cu.5          5.71582
   -5.42250   -1.80750    0.00000  1  Cu.5          5.71582
    1.80750   -5.42250    0.00000  1  Cu.5          5.71582
   -1.80750   -5.42250    0.00000  1  Cu.5          5.71582
    5.42250    0.00000    1.80750  1  Cu.5          5.71582
   -5.42250    0.00000    1.80750  1  Cu.5          5.71582
    0.00000    5.42250    1.80750  1  Cu.5          5.71582
    0.00000   -5.42250    1.80750  1  Cu.5          5.71582
    1.80750    0.00000    5.42250  1  Cu.5          5.71582
   -1.80750    0.00000    5.42250  1  Cu.5          5.71582
    0.00000    1.80750    5.42250  1  Cu.5          5.71582
    0.00000   -1.80750    5.42250  1  Cu.5          5.71582
    5.42250    0.00000   -1.80750  1  Cu.5          5.71582
   -5.42250    0.00000   -1.80750  1  Cu.5          5.71582
    0.00000    5.42250   -1.80750  1  Cu.5          5.71582
    0.00000   -5.42250   -1.80750  1  Cu.5          5.71582
    1.80750    0.00000   -5.42250  1  Cu.5          5.71582
   -1.80750    0.00000   -5.42250  1  Cu.5          5.71582
    0.00000    1.80750   -5.42250  1  Cu.5          5.71582
    0.00000   -1.80750   -5.42250  1  Cu.5          5.71582
    3.61500    3.61500    3.61500  1  Cu.6          6.26136
   -3.61500    3.61500    3.61500  1  Cu.6          6.26136
    3.61500   -3.61500    3.61500  1  Cu.6          6.26136
   -3.61500   -3.61500    3.61500  1  Cu.6          6.26136
    3.61500    3.61500   -3.61500  1  Cu.6          6.26136
   -3.61500    3.61500   -3.61500  1  Cu.6          6.26136
    3.61500   -3.61500   -3.61500  1  Cu.6          6.26136
   -3.61500   -3.61500   -3.61500  1  Cu.6          6.26136
    5.42250    3.61500    1.80750  1  Cu.7          6.76305
   -5.42250    3.61500    1.80750  1  Cu.7          6.76305
    3.61500    5.42250    1.80750  1  Cu.7          6.76305
   -3.61500    5.42250    1.80750  1  Cu.7          6.76305
    5.42250   -3.61500    1.80750  1  Cu.7          6.76305
   -5.42250   -3.61500    1.80750  1  Cu.7          6.76305
    3.61500   -5.42250    1.80750  1  Cu.7          6.76305
   -3.61500   -5.42250    1.80750  1  Cu.7          6.76305
    5.42250    1.80750    3.61500  1  Cu.7          6.76305
   -5.42250    1.80750    3.61500  1  Cu.7          6.76305
    1.80750    5.42250    3.61500  1  Cu.7          6.76305
   -1.80750    5.42250    3.61500  1  Cu.7          6.76305
    5.42250   -1.80750    3.61500  1  Cu.7          6.76305
   -5.42250   -1.80750    3.61500  1  Cu.7          6.76305
    1.80750   -5.42250    3.61500  1  Cu.7          6.76305
   -1.80750   -5.42250    3.61500  1  Cu.7          6.76305
    3.61500    1.80750    5.42250  1  Cu.7          6.76305
   -3.61500    1.80750    5.42250  1  Cu.7          6.76305
    1.80750    3.61500    5.42250  1  Cu.7          6.76305
   -1.80750    3.61500    5.42250  1  Cu.7          6.76305
    3.61500   -1.80750    5.42250  1  Cu.7          6.76305
   -3.61500   -1.80750    5.42250  1  Cu.7          6.76305
    1.80750   -3.61500    5.42250  1  Cu.7          6.76305
   -1.80750   -3.61500    5.42250  1  Cu.7          6.76305
    5.42250    3.61500   -1.80750  1  Cu.7          6.76305
   -5.42250    3.61500   -1.80750  1  Cu.7          6.76305
    3.61500    5.42250   -1.80750  1  Cu.7          6.76305
   -3.61500    5.42250   -1.80750  1  Cu.7          6.76305
    5.42250   -3.61500   -1.80750  1  Cu.7          6.76305
   -5.42250   -3.61500   -1.80750  1  Cu.7          6.76305
    3.61500   -5.42250   -1.80750  1  Cu.7          6.76305
   -3.61500   -5.42250   -1.80750  1  Cu.7          6.76305
    5.42250    1.80750   -3.61500  1  Cu.7          6.76305
   -5.42250    1.80750   -3.61500  1  Cu.7          6.76305
    1.80750    5.42250   -3.61500  1  Cu.7          6.76305
   -1.80750    5.42250   -3.61500  1  Cu.7          6.76305
    5.42250   -1.80750   -3.61500  1  Cu.7          6.76305
   -5.42250   -1.80750   -3.61500  1  Cu.7          6.76305
    1.80750   -5.42250   -3.61500  1  Cu.7          6.76305
   -1.80750   -5.42250   -3.61500  1  Cu.7          6.76305
    3.61500    1.80750   -5.42250  1  Cu.7          6.76305
   -3.61500    1.80750   -5.42250  1  Cu.7          6.76305
    1.80750    3.61500   -5.42250  1  Cu.7          6.76305
   -1.80750    3.61500   -5.42250  1  Cu.7          6.76305
    3.61500   -1.80750   -5.42250  1  Cu.7          6.76305
   -3.61500   -1.80750   -5.42250  1  Cu.7          6.76305
    1.80750   -3.61500   -5.42250  1  Cu.7          6.76305
   -1.80750   -3.61500   -5.42250  1  Cu.7          6.76305
    7.23000    0.00000    0.00000  1  Cu.8          7.23000
   -7.23000    0.00000    0.00000  1  Cu.8          7.23000
    0.00000    7.23000    0.00000  1  Cu.8          7.23000
    0.00000   -7.23000    0.00000  1  Cu.8          7.23000
    0.00000    0.00000    7.23000  1  Cu.8          7.23000
    0.00000    0.00000   -7.23000  1  Cu.8          7.23000
    5.42250    5.42250    0.00000  1  Cu.9          7.66857
   -5.42250    5.42250    0.00000  1  Cu.9          7.66857
    5.42250   -5.42250    0.00000  1  Cu.9          7.66857
   -5.42250   -5.42250    0.00000  1  Cu.9          7.66857
    7.23000    1.80750    1.80750  1  Cu.9          7.66857
   -7.23000    1.80750    1.80750  1  Cu.9          7.66857
    1.80750    7.23000    1.80750  1  Cu.9          7.66857
   -1.80750    7.23000    1.80750  1  Cu.9          7.66857
    7.23000   -1.80750    1.80750  1  Cu.9          7.66857
   -7.23000   -1.80750    1.80750  1  Cu.9          7.66857
    1.80750   -7.23000    1.80750  1  Cu.9          7.66857
   -1.80750   -7.23000    1.80750  1  Cu.9          7.66857
    5.42250    0.00000    5.42250  1  Cu.9          7.66857
   -5.42250    0.00000    5.42250  1  Cu.9          7.66857
    0.00000    5.42250    5.42250  1  Cu.9          7.66857
    0.00000   -5.42250    5.42250  1  Cu.9          7.66857
    1.80750    1.80750    7.23000  1  Cu.9          7.66857
   -1.80750    1.80750    7.23000  1  Cu.9          7.66857
    1.80750   -1.80750    7.23000  1  Cu.9          7.66857
   -1.80750   -1.80750    7.23000  1  Cu.9          7.66857
    7.23000    1.80750   -1.80750  1  Cu.9          7.66857
   -7.23000    1.80750   -1.80750  1  Cu.9          7.66857
    1.80750    7.23000   -1.80750  1  Cu.9          7.66857
   -1.80750    7.23000   -1.80750  1  Cu.9          7.66857
    7.23000   -1.80750   -1.80750  1  Cu.9          7.66857
   -7.23000   -1.80750   -1.80750  1  Cu.9          7.66857
    1.80750   -7.23000   -1.80750  1  Cu.9          7.66857
   -1.80750   -7.23000   -1.80750  1  Cu.9          7.66857
    5.42250    0.00000   -5.42250  1  Cu.9          7.66857
   -5.42250    0.00000   -5.42250  1  Cu.9          7.66857
    0.00000    5.42250   -5.42250  1  Cu.9          7.66857
    0.00000   -5.42250   -5.42250  1  Cu.9          7.66857
    1.80750    1.80750   -7.23000  1  Cu.9          7.66857
   -1.80750    1.80750   -7.23000  1  Cu.9          7.66857
    1.80750   -1.80750   -7.23000  1  Cu.9          7.66857
   -1.80750   -1.80750   -7.23000  1  Cu.9          7.66857

 END

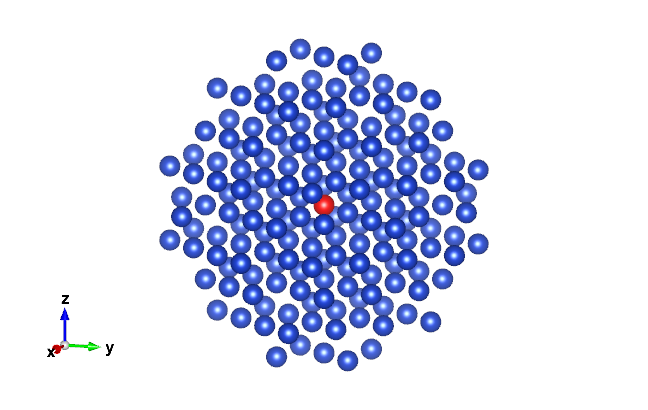
Cu 単一元素しか含まれていないので見ても面白くありませんが、VESTA 5で可視化したものが以下の図です。吸収原子のみ、赤くしておきました。

feff.png

FEFF の実行

feff.inp を同じディレクトリに入れ、FEFF を実行しましょう。前述のようにDemeter パッケージにはFEFF6L が同梱されているので、それを利用できます。もちろん有料版のFEFF を持っている方はそちらを使っても問題ありません。

FEFF を実行すると様々なファイルが生成されますが、その中でfeffNNNN.dat (NNNN は0埋めされた四桁の整数) というファイル群が各散乱パスに対応します。今回のfeff.inp だと、25 個のfeffNNNN.dat が生成されるはずです。これらのファイルを./feffpath ディレクトリに保存しておきます。

EXAFS スペクトルのシミュレーション

散乱パスの読み込み

散乱パスのファイル名(feffNNNN.dat) を指定してlp.xafs.FeffPathGroup クラスのインスタンスを作ると、FEFFで計算した散乱パスを読み込むことができます。

In[3]
fp = lp.xafs.FeffPathGroup(filename='./feffpath/feff0001.dat', _larch=session)

FeffPathGroup クラスには、様々な属性が設定されています。アクセス可能な属性の一覧を以下に示します。

属性名 カテゴリー 説明
filename 情報 ファイル名(feffNNNN.dat)
label 情報 パスの説明
geom 情報 散乱パスのジオメトリー: (symbol, ipot, x, y, z) のリスト
reff 数値(固定) $R_{\mathrm{eff}}$, 散乱パス長
nleg 数値(固定) 足(leg)の数 (散乱回数+1)
degen 数値(可変) $N$, 多重度, 配位数のこと
s02 数値(可変) $S^2_0$, 多体効果の補正項
e0 数値(可変) $E_0$, エネルギー原点
deltar 数値(可変) $\Delta R$, パス長の変化
sigma2 数値(可変) $\sigma^2$, 平均自乗変位、デバイワーラー因子
third 数値(可変) $c_3$, 3次のキュムラント
fourth 数値(可変) $c_4$, 4次のキュムラント
ei 数値(可変) $E_i$, 虚部のエネルギーシフト
k 出力(ndarray) $k_{\mathrm{feff}}$, 光電子の波数
chi 出力(ndarray) $\chi$, EXAFS スペクトル
chi_imag 出力(ndarray) $\Im[{\chi}]$, EXAFS の虚部
p 出力(ndarray) p, 複素数に拡張された光電子の波数
_feffdat Group lp.xafs.feffdat.FeffDatFile インスタンス

この中の_feffdat はlp.xafs.feffdat.FeffDatFile クラスのインスタンスですが、FeffPathGroup よりも更に詳細な情報が格納されています。FeffPathGroup と重複してない項目をいくつか示します。

属性名 説明
amp ndarray: 散乱振幅 (mag_feff * red_fact)
edge 吸収端エネルギー(単原子の値に対する相対値)
gam_ch 内殻の寿命幅
kf Fermi 準位での$k$ の値
lam ndarray: 平均自由行程, $\lambda(k)$
mag_feff ndarray: 有効散乱振幅, $f_{\mathrm{eff}}$
mu Fermi 準位(eV)
pha ndarray: 位相シフト, $\delta(k)$
pha_feff ndarray: 散乱による位相シフト
potentials ポテンシャルの情報: (ipot, z, r_MuffinTin, r_Norman)のリスト
real_phc ndarray: 中心原子の位相シフト
red_fact ndarray: 振幅減衰因子
rep ndarray: $p$ の実部, $p_{\mathrm{real}}(k)$

EXAFS 振動の計算

Larch では、前節の表で示した散乱パスに関するパラメータから、以下の式を使ってEXAFS スペクトルを計算しています。

$$
k = \sqrt{k_{\rm feff}^2 - {2m_e E_0}/{\hbar^2} }
$$

$$
p = p' + i p'' = \sqrt{ \big[ p_{\rm real}(k) - i / \lambda(k) \big]^2 - i \, 2 m_e E_i /{\hbar^2} }
$$

$$
\chi(k) = {\rm Im} \left[{\displaystyle{ \frac{f_{\rm eff}(k) N S_0^2} {k(R_{\rm eff} + \Delta R)^2} } \exp(-2p''R_{\rm reff} - 2p^2\sigma^2 + \textstyle{\frac{2}{3}}p^4 c_4)} { \\ \hspace{80pt} \times \exp { i\big[ 2kR_{\rm eff} + \delta(k) + 2p(\Delta R - 2\sigma^2/R_{\rm eff} ) - \textstyle{\frac{4}{3}} p^3 c_3 \big] } } \right]
$$

実際に計算するには、FeffPathGroup クラスのメソッドである_calc_chi を使います。このメソッドの引数には、FeffPathGroup 属性表のパラメータが設定可能です。ここではひとまず、sigma2 のみ0.004 として計算してみます。

In[4]
fp._calc_chi(sigma2=0.005)
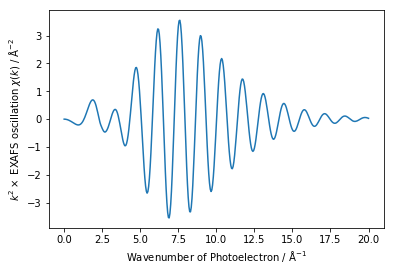
plt.plot(fp.k, fp.chi*fp.k**2)
plt.xlabel("Wavenumber of Photoelectron / $\mathrm{\AA}^{-1}$")
plt.ylabel("$k^2 \\times$ EXAFS oscillation $\chi (k)$ / $\mathrm{\AA}^{-2}$")
plt.show()

download1.png

_calc_chi を実行すると、k, chi, chi_mag, p 属性に値が出力されます。k が光電子の波数で、chi がEXAFS スペクトルなので、k に対してchi をプロットしてやればEXAFS 振動をプロットしたことになります。

次に、このパスの動径構造関数を計算します。これには、実験結果と同様にlp.xafs.xftf を使います。ただし、lp.xafs.xftf は計算結果をGroup インスタンスに出力しますので、先に結果を受け取るためのGroup インスタンスを作成しておく必要があります。

In[5]
# make Group instance for outputs
from larch.symboltable import Group
fp_group = Group()
# calc EXAFS spectrum
fp._calc_chi(sigma2=0.004)
# fourier transform
lp.xafs.xftf(fp.k, fp.chi, kweight=2, kmin=3, kmax=15, dk=1.0, window='hanning', group=fp_group, _larch=session)
# plot
plt.plot(fp_group.r, fp_group.chir_mag)
plt.xlim(0, 6)
plt.xlabel("Radial distance / $\mathrm{\AA}$")
plt.ylabel("Magnitude of Fourier Transform of $k^2 \cdot \chi$ / $\mathrm{\AA}^{-3}$")
plt.show()

download2.png

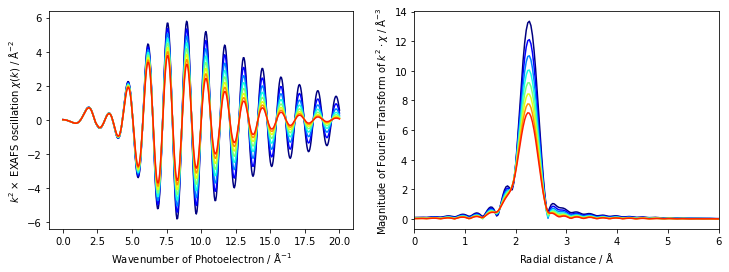
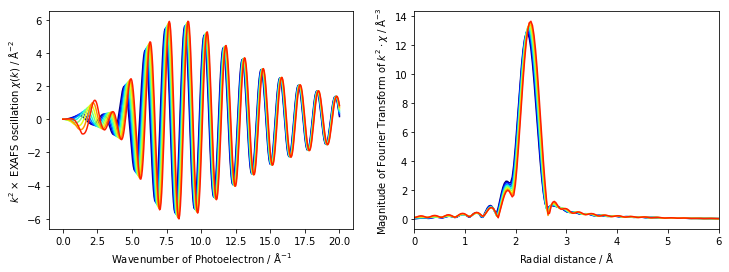
この_calc_chi は非常に便利で、例えばパラメータを変化させたときにEXAFS 振動がどのように変化するかの検証に使えます。sigma2, deltar, s02, e0 の数値を振ったときのEXAFS 振動・動径構造関数の変化を見てみましょう。

In[6]
sigma2 = np.arange(0.001, 0.005, 0.0005)

fig = plt.figure(figsize=(12, 4))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)

for i, s in enumerate(sigma2):
    fp._calc_chi(deltar=0, s02=1, sigma2=s)
    fp_group = Group()
    lp.xafs.xftf(fp.k, fp.chi, kweight=2, kmin=3, kmax=15, dk=1.0, window='hanning', group=fp_group, _larch=session)
    ax1.plot(fp.k, fp.chi*fp.k**2, color=cm.jet(float(i) / len(sigma2)))
    ax1.set_xlabel("Wavenumber of Photoelectron / $\mathrm{\AA}^{-1}$")
    ax1.set_ylabel("$k^2 \\times$ EXAFS oscillation $\chi (k)$ / $\mathrm{\AA}^{-2}$")
    ax2.plot(fp_group.r, fp_group.chir_mag, color=cm.jet(float(i) / len(sigma2)))
    ax2.set_xlim(0, 6)
    ax2.set_xlabel("Radial distance / $\mathrm{\AA}$")
    ax2.set_ylabel("Magnitude of Fourier Transform of $k^2 \cdot \chi$ / $\mathrm{\AA}^{-3}$")
plt.show()

output_26_0.png

sigma2 が大きくなると、EXAFS 振動は減衰することがわかります。また、k が大きいほど減衰が大きいことが分かります。

In[7]
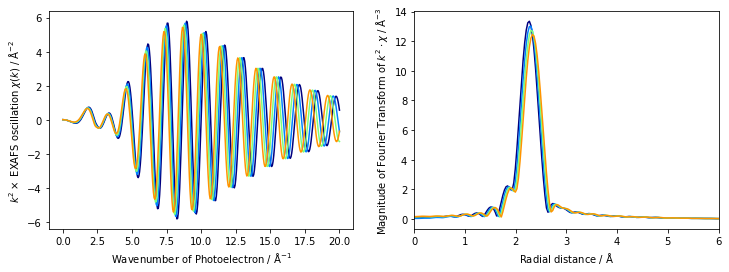
delr = np.arange(0.0, 0.1, 0.025)

fig = plt.figure(figsize=(12, 4))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)

for i, r in enumerate(delr):
    fp._calc_chi(deltar=r, s02=1, sigma2=0.001)
    fp_group = Group()
    lp.xafs.xftf(fp.k, fp.chi, kweight=2, kmin=3, kmax=15, dk=1.0, window='hanning', group=fp_group, _larch=session)
    ax1.plot(fp.k, fp.chi*fp.k**2, color=cm.jet(float(i) / len(delr)))
    ax1.set_xlabel("Wavenumber of Photoelectron / $\mathrm{\AA}^{-1}$")
    ax1.set_ylabel("$k^2 \\times$ EXAFS oscillation $\chi (k)$ / $\mathrm{\AA}^{-2}$")
    ax2.plot(fp_group.r, fp_group.chir_mag, color=cm.jet(float(i) / len(delr)))
    ax2.set_xlim(0, 6)
    ax2.set_xlabel("Radial distance / $\mathrm{\AA}$")
    ax2.set_ylabel("Magnitude of Fourier Transform of $k^2 \cdot \chi$ / $\mathrm{\AA}^{-3}$")
plt.show()

output_27_0.png

deltar が変化すると、振動周期が変化することが分かります。一方、振幅は若干の変化しかしていません。当然、フーリエ変換である動径構造関数のピーク位置はシフトします。

In[8]
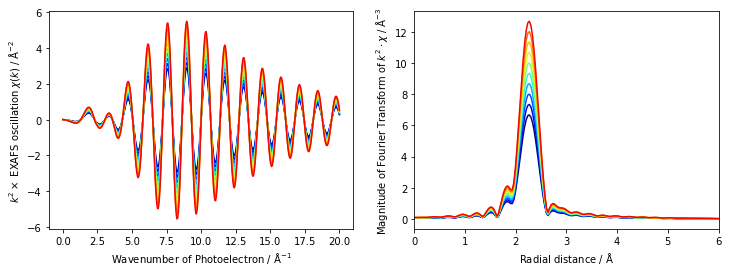
s02 = np.arange(0.5, 1.0, 0.05)

fig = plt.figure(figsize=(12, 4))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)

for i, s in enumerate(s02):
    fp._calc_chi(deltar=0.0, s02=s, sigma2=0.001)
    fp_group = Group()
    lp.xafs.xftf(fp.k, fp.chi, kweight=2, kmin=3, kmax=15, dk=1.0, window='hanning', group=fp_group, _larch=session)
    ax1.plot(fp.k, fp.chi*fp.k**2, color=cm.jet(float(i) / len(s02)))
    ax1.set_xlabel("Wavenumber of Photoelectron / $\mathrm{\AA}^{-1}$")
    ax1.set_ylabel("$k^2 \\times$ EXAFS oscillation $\chi (k)$ / $\mathrm{\AA}^{-2}$")
    ax2.plot(fp_group.r, fp_group.chir_mag, color=cm.jet(float(i) / len(s02)))
    ax2.set_xlim(0, 6)
    ax2.set_xlabel("Radial distance / $\mathrm{\AA}$")
    ax2.set_ylabel("Magnitude of Fourier Transform of $k^2 \cdot \chi$ / $\mathrm{\AA}^{-3}$")
plt.show()

output_28_0.png

s02 はsigma2 と同様に振幅に作用します。ただし、sigma2 とは異なり、減衰の仕方にk 依存性がありません。

In[9]
e0 = np.arange(-10.0, 10.0, 2.5)

fig = plt.figure(figsize=(12, 4))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)

for i, e in enumerate(e0):
    fp._calc_chi(deltar=0.0, s02=1.0, sigma2=0.001, e0=e)
    fp_group = Group()
    lp.xafs.xftf(fp.k, fp.chi, kweight=2, kmin=3, kmax=15, dk=1.0, window='hanning', group=fp_group, _larch=session)
    ax1.plot(fp.k, fp.chi*fp.k**2, color=cm.jet(float(i) / len(e0)))
    ax1.set_xlabel("Wavenumber of Photoelectron / $\mathrm{\AA}^{-1}$")
    ax1.set_ylabel("$k^2 \\times$ EXAFS oscillation $\chi (k)$ / $\mathrm{\AA}^{-2}$")
    ax2.plot(fp_group.r, fp_group.chir_mag, color=cm.jet(float(i) / len(e0)))
    ax2.set_xlim(0, 6)
    ax2.set_xlabel("Radial distance / $\mathrm{\AA}$")
    ax2.set_ylabel("Magnitude of Fourier Transform of $k^2 \cdot \chi$ / $\mathrm{\AA}^{-3}$")
plt.show()

output_29_0.png

e0 はdeltar と同様に振動周期に作用します。

以上の変化はEXAFS の計算式から自明な結果ですが、実際にどの程度の変化が生じるかを把握することは重要かと思います。その点で、Python + Larch はArtemis でシミュレーションを行うよりも、パラメータを振った結果を一挙に可視化できて便利です。

パスの合成

今回の例では、feffNNNN.dat は25 個あります。これらのパスを一挙に読み込んで、合成（足し合わせ）することが出来ます。まずはパスを読み込みましょう。以下のようにします。

In[10]
import glob
dat_list = glob.glob('feffpath/*')
paths = []

for i, f in enumerate(dat_list):
    i = i + 1
    num_string = str(i).zfill(4)
    exec('path'+num_string+' = lp.xafs.FeffPathGroup(filename=f, _larch=session)')
    exec('path'+num_string+'._calc_chi(sigma2=0.004)')
    exec('paths.append(path'+num_string+')')

読み込み方はお好みですが、ここではexec を使って、feffNNNN.dat から読み込んだ散乱パスをpathNNNN という名前の変数にしています。また、それらの変数はすべてpaths 変数にリストとしてまとめています。

次に、paths に入っている全散乱パスを足し合わせてプロットしてみます。

In[11]
all_path_sum = np.zeros(paths[0].k.shape)
k_calc = paths[0].k
for p in paths:
    all_path_sum += p.chi

all_path_group = Group()
lp.xafs.xftf(k_calc, all_path_sum, kweight=2, kmin=3, kmax=15, dk=1.0, window='hanning', group=all_path_group, _larch=session)

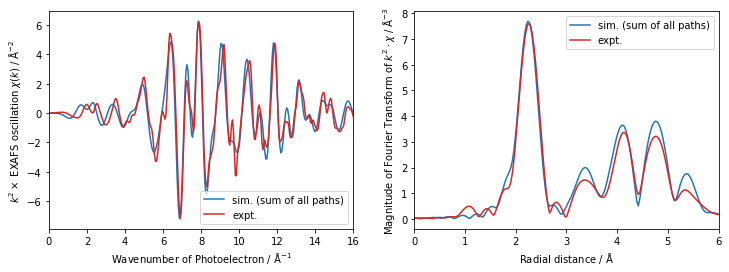
fig = plt.figure(figsize=(12, 4))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
ax1.plot(k_calc+0.1, all_path_sum*tmp.k**2, label='sim. (sum of all paths)')
ax1.plot(Cu_expt.k, Cu_expt.chi*Cu_expt.k**2, label='expt.')
ax1.set_xlim(0, 16)
ax1.set_xlabel("Wavenumber of Photoelectron / $\mathrm{\AA}^{-1}$")
ax1.set_ylabel("$k^2 \\times$ EXAFS oscillation $\chi (k)$ / $\mathrm{\AA}^{-2}$")
ax1.legend()
ax2.plot(all_path_group.r, all_path_group.chir_mag, label='sim. (sum of all paths)')
ax2.plot(Cu_expt.r, Cu_expt.chir_mag, label='expt.')
ax2.set_xlim(0, 6)
ax2.set_xlabel("Radial distance / $\mathrm{\AA}$")
ax2.set_ylabel("Magnitude of Fourier Transform of $k^2 \cdot \chi$ / $\mathrm{\AA}^{-3}$")
ax2.legend()
plt.show()

output_34_0.png

$\chi(k)$ の方では少し計算結果の横軸をシフトさせる必要がありますが、概ね一致しているように見えます。実際には、すべてのパスでsigma2=0.004 になることは無いですし他のパラメータも若干変化しますので、このくらい実験結果と良く合っているというのは、むしろ驚きでしょう。

全てのパスではなく、特定のパスのみを合成することも当然可能です。以下ではその例として、一回散乱のパスのみを足し合わせてみます。pathNNNN はFeffPathGroup クラスのインスタンスなので、前述の散乱パスの情報が含まれています。たとえば、nleg には散乱経路の数が入っています。

In[12]
path0001.nleg
Out[12]
2

一回散乱のときのみnleg が2 となるので、nleg の値を判定に使えば選別が可能です。

In[13]
ss_path_sum = np.zeros(paths[0].k.shape)
k_calc = paths[0].k

for p in paths:
    if p.nleg == 2:
        ss_path_sum += p.chi

これで一回散乱のパスのみを足し合わせることが出来ました。プロットしてみます。

In[14]
ss_path_group = Group()
lp.xafs.xftf(k_calc, ss_path_sum, kweight=2, kmin=3, kmax=15, dk=1.0, window='hanning', group=ss_path_group, _larch=session)

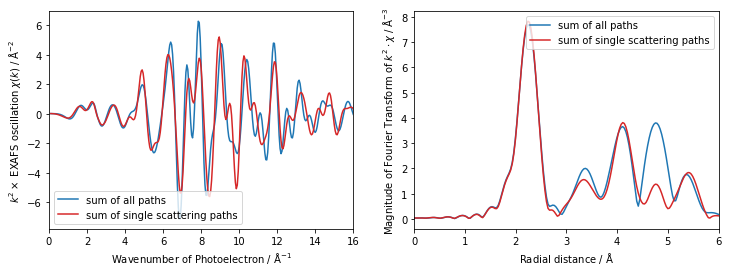
fig = plt.figure(figsize=(12, 4))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
ax1.plot(k_calc+0.1, all_path_sum*tmp.k**2, label='sum of all paths')
ax1.plot(k_calc+0.1, ss_path_sum*tmp.k**2, label='sum of single scattering paths')
ax1.set_xlim(0, 16)
ax1.set_xlabel("Wavenumber of Photoelectron / $\mathrm{\AA}^{-1}$")
ax1.set_ylabel("$k^2 \\times$ EXAFS oscillation $\chi (k)$ / $\mathrm{\AA}^{-2}$")
ax1.legend()
ax2.plot(all_path_group.r, all_path_group.chir_mag, label='sum of all paths')
ax2.plot(ss_path_group.r, ss_path_group.chir_mag, label='sum of single scattering paths')
ax2.set_xlim(0, 6)
ax2.set_xlabel("Radial distance / $\mathrm{\AA}$")
ax2.set_ylabel("Magnitude of Fourier Transform of $k^2 \cdot \chi$ / $\mathrm{\AA}^{-3}$")
ax2.legend(loc='upper right')
plt.show()

output_40_0.png

一回散乱の合成では二回以上の散乱を無視しているため、全散乱パスの合成結果とは異なるスペクトル形状になっています。他にも、散乱パス長の範囲を指定して足し合わせる、等の応用が考えられます。

EXAFS スペクトルのフィッティング

Larch によるEXAFS スペクトルのフィッティングの流れは以下の通りになります。

  1. フィッティングパラメータをまとめたGroup インスタンスを作る。
  2. FEFF で計算した散乱パスを読み込む。
  3. lp.xafs.TransformGroup を作成する。
  4. lp.xafs.FeffitDataSet を作成する。
  5. lp.xafs.feffit でフィッティングを行う。

以下で、Cu 箔の動径構造関数の第一ピークに対するフィッティングを例として各ステップを詳細に説明します。

まず、フィッティング用のパラメータを設定して、Group インスタンスにまとめます。Larch では、フィッティングにPython ライブラリであるlmfit (Larch と作者が同じ) を利用しています。以下ではLarch からParameter をimport しますが、これはlmfit のParameter そのものです。もし分からないことがあれば、lmfit のドキュメントを見ると良いでしょう。

パラメータ名を属性名として、Parameter インスタンスをまとめたGroup を作ります。このとき、value に初期値を、vary に可変かどうかを指定します。また、今は指定しませんがmin, max にそれぞれ最小値・最大値（フィッティング中の可変域）を指定可能です。

今回は、一回散乱のパスを一つだけフィッティングするので、amp, del_e0, sig2, del_r という名前の4つのパラメータを設定します。

In[15]
from larch import Group, Parameter

pars = Group(amp    = Parameter(value=1.0, vary=True),
             del_e0 = Parameter(value=0.0, vary=True),
             sig2   = Parameter(value=0.0, vary=True),
             del_r  = Parameter(value=0.0, vary=True),
             _larch=session)

次に、散乱パスを読み込みます。このとき、s02, e0, sigma2, deltar にそれぞれamp, del_e0, sig2, del_r を文字列で指定します。

In[16]
path1 = lp.xafs.FeffPathGroup(filename = 'feffpath/feff0001.dat',
                              s02      = 'amp',
                              e0       = 'del_e0',
                              sigma2   = 'sig2',
                              deltar   = 'del_r',
                              _larch=session)

さて、XAFS のフィッティングと一言で言っても、

  • 動径構造関数のフィッティング(R 空間)
  • 動径構造関数の特定範囲を逆フーリエ変換したものをフィッティング（Q 空間）
  • EXAFS 振動をそのままフィッティング(k 空間)

といった方法があります。また、測定データとシミュレーション結果の双方を（フーリエ変換等で）変形する必要があります。これらの条件を設定するのがlp.xafs.TransformGroup です。フィッティング方法はfitspace で、上から順に'r', 'q', 'k' で指定が可能です。それ以外にフーリエ変換のパラメータとしてkmin, kmax, kw, dk, window を、フィッティング範囲としてrmin, rmax を指定します。

In[17]
trans = lp.xafs.TransformGroup(fitspace='r', kmin=3, kmax=14, kw=2, dk=1, window='hanning', rmin=1.4, rmax=3.0, _larch=session)

実験結果とモデルおよび上記のTransformGroup をまとめたオブジェクトがlp.xafs.FeffitDataSet です。フィッティング結果のスペクトル等も、このFeffitDataSet に格納されます。data に実験結果のGroup インスタンスを、pathlist にフィッティングに用いるパスを、transform に先程作ったTransformGroup を指定します。

In[18]
dset = lp.xafs.FeffitDataSet(data=Cu_expt, pathlist=[path1], transform=trans, _larch=session)

最後に、lp.xafs.feffit を用いてフィッティングを実行します。第一引数にパラメータGroup を、第二引数にFeffitDataSet を指定します。

In[19]
out = lp.xafs.feffit(pars, dset, _larch=session)

out という名前の変数に入れたlp.xafs.feffit の実行結果は、Group クラスのインスタンスになり、フィッティング結果に関する情報は属性でアクセス可能になります。また、フィッティング結果のEXAFS 振動・動径構造関数等は、lp.xafs.feffit の実行時に指定したFeffitDataSet インスタンスに格納されます。

実験結果およびフィッティング結果の動径構造関数の大きさと実部をそれぞれプロットしてみます。フィッティング結果のシミュレーション・実験結果は、FeffitDataSet のサブクラスであるmodel およびdata に格納されています。

In[20]
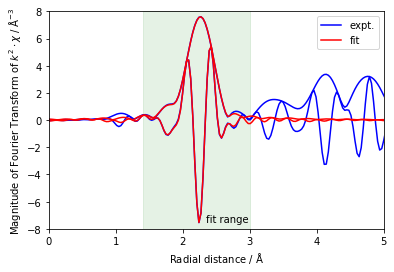
fig = plt.figure()
plt.plot(dset.data.r, dset.data.chir_mag, color='b')
plt.plot(dset.data.r, dset.data.chir_re, color='b', label='expt.')
plt.plot(dset.model.r, dset.model.chir_mag, color='r')
plt.plot(dset.model.r, dset.model.chir_re, color='r', label='fit')
plt.ylabel("Magnitude of Fourier Transform of $k^2 \cdot \chi$ / $\mathrm{\AA}^{-3}$")
plt.xlabel("Radial distance / $\mathrm{\AA}$")
plt.xlim(0, 5)
plt.ylim(-8, 8)
plt.fill([1.4, 1.4, 3.0, 3.0],[-8, 8, 8, -8], color='g',alpha=0.1)
plt.text(2.35, -7.5, 'fit range')
plt.legend()
plt.show()

output_46_0.png

良く一致する結果が得られていることが分かります。

フィッティング結果のR 因子等の統計的な情報や精密化されたパラメータはout (pars にも精密化されたパラメータが格納されている)に入っており属性でアクセスすることが可能ですが、一覧で表示するにはfeffit_report メソッドが便利です。ただし、feffit_report メソッドはpython からは利用できません。これでは不便ですので、一行だけLarch ライブラリのソースコードを書き換えてしまいます。$PYTHON_ROOT/share/larch/plugins/xafs/__init__.py の9行目を以下のように変更します。

変更前
from .feffit import FeffitDataSet, TransformGroup, feffit
変更後
from .feffit import FeffitDataSet, TransformGroup, feffit, feffit_report

単にfeffit.py からfeffit_report をimport しただけです。これで、lp.xafs.feffit_report として利用が可能になります。（他にも使いたいメソッドがあれば、同様にimport することでPython から利用可能になります。）lp.xafs.feffit_report はフィッティングのサマリーを文字列で出力しますので、print に渡してやりましょう。

In[21]
print lp.xafs.feffit_report(out, _larch=session)
Out[21]
    =================== FEFFIT RESULTS ====================
    [[Statistics]]
       nvarys, npts       = 4, 104
       n_independent      = 12.205
       chi_square         = 63.0448
       reduced chi_square = 7.68417
       r-factor           = 0.00091
       Akaike info crit   = 28.0403
       Bayesian info crit = 30.0475

    [[Data]]
       fit space          = 'r'
       r-range            = 1.400, 3.000
       k-range            = 3.000, 14.000
       k window, dk       = 'hanning', 1.000
       paths used in fit  = ['feffpath/feff0001.dat']
       k-weight           = 2
       epsilon_k          = Array(mean=0.001607, std=0.002755)
       epsilon_r          = 0.033235
       n_independent      = 12.205

    [[Variables]]
       amp            =  0.898859 +/- 0.021936   (init=  1.000000)
       del_e0         =  5.937448 +/- 0.297522   (init=  0.000000)
       del_r          = -0.013912 +/- 0.001366   (init=  0.000000)
       sig2           =  0.003512 +/- 0.000150   (init=  0.000000)

    [[Correlations]]    (unreported correlations are <  0.100)
       amp, sig2            =  0.902
       del_e0, del_r        =  0.887
       amp, del_r           =  0.146
       del_r, sig2          =  0.144

    [[Paths]]
       Path poimlskgi, Feff.dat file = feffpath/feff0001.dat
         atom      x        y        z       ipot
          Cu       0.0000,  0.0000,  0.0000  0 (absorber)
          Cu      -1.8075,  0.0000,  1.8075  1
         reff   =  2.55620
         degen  =  12.000000
         n*s02  =  0.898859 +/- 0.021936  'amp'
         e0     =  5.937448 +/- 0.297522  'del_e0'
         r      =  2.542288 +/- 0.001366  'reff + del_r'
         deltar = -0.013912 +/- 0.001366  'del_r'
         sigma2 =  0.003512 +/- 0.000150  'sin(sig2)'

    =======================================================

必要な情報はほぼ全て表示できていますね。

まとめ

Larch を用いてEXAFS のフィッティングを行う方法をまとめました。パラメータを詳細に振った解析が容易に行えるのがLarch の強みです。真面目かつ効率的にXAFS 解析をしたい人にはおすすめです。

  1. The FEFF Project : http://monalisa.phys.washington.edu/feffproject-feff.html ↩

  2. Demeter : https://bruceravel.github.io/demeter/ ↩

  3. 発展途上というか、あまりPython から使うことを想定してないっぽいという印象。ドキュメントではhttp://xraypy.github.io/xraylarch/xafs/feffpaths.html#running-feff のあたりがFEFF の操作に対応する。。 ↩

  4. Python からLarch を利用してXAFS 解析: https://qiita.com/inashiro/items/f1c10440618cf73a2d81 ↩

  5. K. Momma and F. Izumi, "VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data," J. Appl. Crystallogr., 44, 1272-1276 (2011). ↩

3
1
4

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
1