larch ライブラリとは
以下の公式サイトから引用
http://xraypy.github.io/xraylarch/
Larch is an open-source library and toolkit for processing and analyzing X-ray spectroscopic and scattering data collected at modern synchrotron sources. It also provides a wide selection of tools for organizing complex data sets and processing and analyzing arrays of scientific data.
端的に言うと、XAFS(X-ray Absorption Fine Structure) 解析用のライブラリ・ツールです。ATHENA/ARTEMIS でもバックエンドで利用されているらしいですが、そちらのコードを確認してないので、どのように使われているかは知りません。独自記法のスクリプト言語で利用するようになっていますが、中身はPython で書かれたものなので、当然のごとくPython から呼んで利用できます。いちいち新しい記法なんか覚えて(ry
XAFS だけでなく、XRF や最近だとXRD のデータも扱えるようになっているようです。
コード・ドキュメント共に割と頻繁に更新されていて、例えば最近気づいたらLarch からローカルのFEFF が動かせるようになってたりしました。定期的にチェックすると良いでしょう。
余談ですが、Larch は英語でカラマツを意味するようです。公式サイトには松ぼっくりっぽい画像があります。
larch ライブラリのimport 1
公式ドキュメントだとlarch_plugins.hoge から必要なメソッドをいちいちimport するようになっているが、面倒かつ煩雑です。ここではlarch_plugins をいったん丸ごとimport し、そこから必要に応じてメソッドを呼び出していく方法をとります。
また、Larch のメソッドの多くは、larch.Interpreter インスタンスを引数に指定する必要があります。ここでは、session という名前のインスタンスを作ります。
import larch_plugins as lp
from larch import Interpreter
session = Interpreter()
注意点として、Jupyter Notebookを使っている場合、matplotlib の読み込みやマジックコマンド(%matplotlib inlineとか)はlarch のimport の前に行っておいた方が良いようです。
公式サイトのインストール方法(anaconda を利用する、とか) を踏襲すると、ライブラリのimport 時に警告が出る(自分はpyFAI関連の警告が大量に出ます)場合がありますが、単なるXAFS データ処理のメソッドを利用する分には問題ないことが多いので、無視してもかまいません。気になるようなら原因を特定して、GitHubで作成者グループに報告してあげると喜ばれるかもしれません。
ファイルの読み込み
テストとして、XAFS データベースから拾ってきたCu 箔の低温での測定結果を読み込んでみます。
XAFSデータベース
https://www.cat.hokudai.ac.jp/catdb/
今回は"K_Cu12.5K_Si111_20101108.txt" というファイルを読み込みますが、このファイルは、
8475.48 0.70398
8482.02 0.70056
8488.57 0.69701
8495.01 0.69357
...
というように、一列目が入射X線のエネルギー、二列目が吸収係数に厚みを掛けた$\mu t$ になっています。
このような測定結果のテキストファイルを読み込むには、larch_plugins.io.read_ascii メソッドを使います。読み込みに際しては、列ごとにラベルを設定できますが、エネルギーの列には"energy"、吸収係数の列には"mu" を割り振っておくと良いでしょう。labels に、左から順に列のラベル名をスペース区切りで指定します。
dat = lp.io.read_ascii("./K_Cu12.5K_Si111_20101108.txt", labels="energy mu", _larch=session)
このようにして読み込んだデータは、larch.symboltable.Group クラスのインスタンスになります。
type(dat)
>> larch.symboltable.Group
上記で設定したラベルはそのまま属性の名称となっていて、アクセスが可能です。この属性の数値データ列は1
次元のndarray となっています。
type(dat.energy)
>> numpy.ndarray
つまり、これらの数値データに対して、一般のnumpy, scipy メソッドを適用することが可能です。当然、matplotlib によるグラフ化も可能です。
とりあえず、そのままEnergy に対して$\mu t$ をプロットしてみましょう。
fig = plt.figure(figsize=(8, 4))
plt.plot(dat.energy, dat.mu)
plt.xlabel("Photon energy / eV")
plt.ylabel("Absorbance")
plt.show()
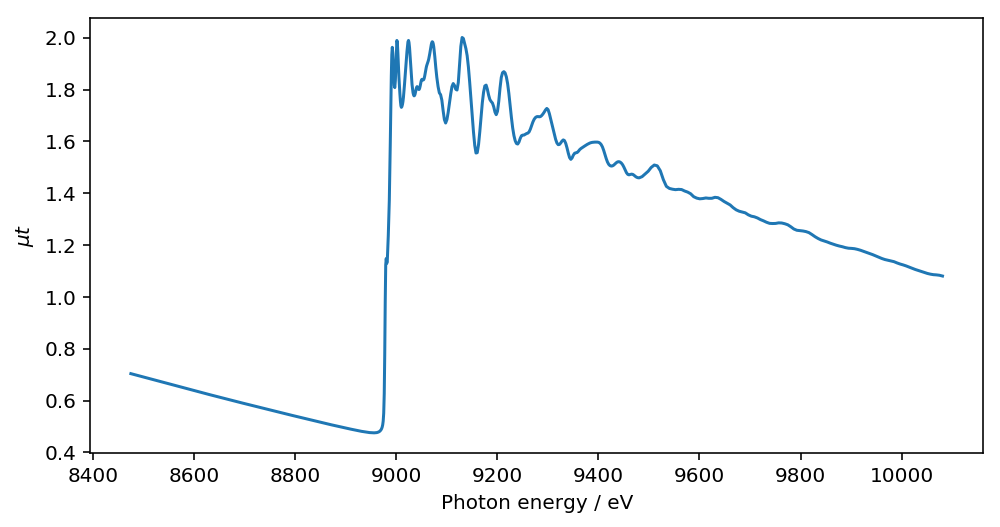
グラフ化できました。透過法の測定結果で、ジャンプもだいたい1 くらいの良いデータですね。
読み込んだデータの処理
read_ascii でデータを読み込むことで生成されるlarch.symboltable.Group インスタンスに対して種々のメソッドを作用させることで、一般的に行われるXAFS データ処理のほとんどが実現可能です。
以下では、バックグラウンド除去と規格化、EXAFS 振動の抽出、動径構造関数の導出(フーリエ変換)について順を追って見ていきます。メソッドを適用することによる一般的な挙動は規格化のところで確認します。
バックグラウンド除去および規格化
larch_plugins.xafs.pre_edge メソッドによって、Pre-edge のバックグラウンド除去およびXAFS スペクトルの規格化が可能です。このメソッドはGroup インスタンスを引数にとります。また、今後のすべてのメソッドについて言えることですが、Interpreter インスタンスを_larch に指定してやる必要があります。
ひとまず、実行してみましょう。
lp.xafs.pre_edge(dat, _larch=session)
何も値が返ってきません。型を確かめてみましょう。
type(lp.xafs.pre_edge(dat, _larch=session))
>> NoneType
NoneType です。
このように、larch ライブラリのメソッドは値を返しません。 それでは、メソッドを実行したことにより何が起きたのか?というと、引数で指定したGroup インスタンスに属性が追加されます。
pre_edge メソッドでは、いくつかの属性が追加されますが、そのうちのnorm という名称の属性にバックグラウンド除去および規格化された数値データが格納されます。
ためしに、dat.energy に対してdat.norm をプロットしてみましょう。
fig = plt.figure(figsize=(8, 4))
plt.plot(dat.energy, dat.norm, label="normalized XAFS spectrum")
plt.xlabel("Photon energy / eV"); plt.ylabel("normalized $\mu t$"); plt.legend()
plt.show()
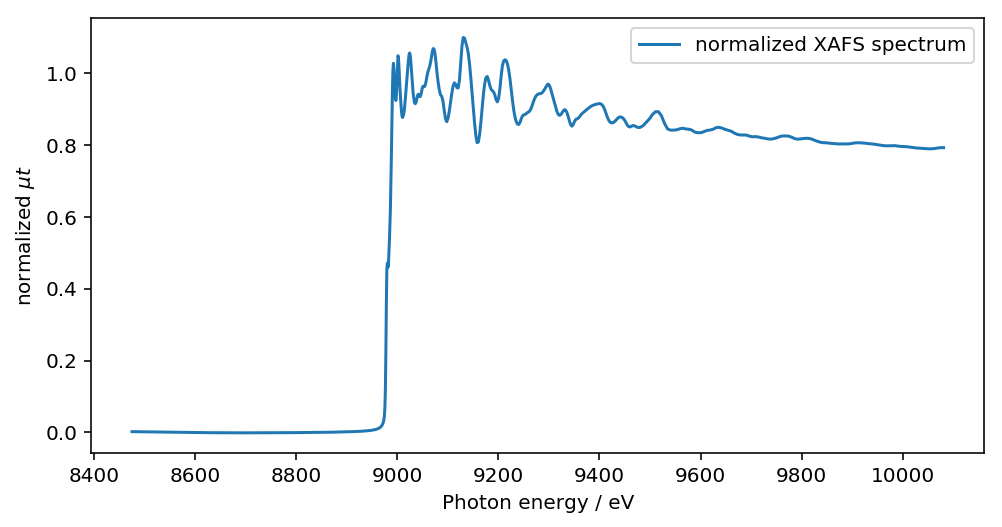
XAFS スペクトルが規格化されたことが確認できます。(ただし、Athena でのデフォルトの処理結果と異なり、post edge 部が規格化強度1.0にフラット化されていない点に注意が必要です。)
他にも、pre_edge, post_edge という属性が追加されており、これらにはPre edge およびPost edge のバックグラウンドが格納されています。
fig = plt.figure(figsize=(8, 4))
plt.plot(dat.energy, dat.pre_edge, linestyle=":", color="k", label="pre edge line")
plt.plot(dat.energy, dat.mu, label="raw $\mu t$")
plt.plot(dat.energy, dat.post_edge,linestyle="--", color="k", label="post edge line")
plt.xlabel("Photon energy / eV"); plt.ylabel("$\mu t$"); plt.legend()
plt.show()
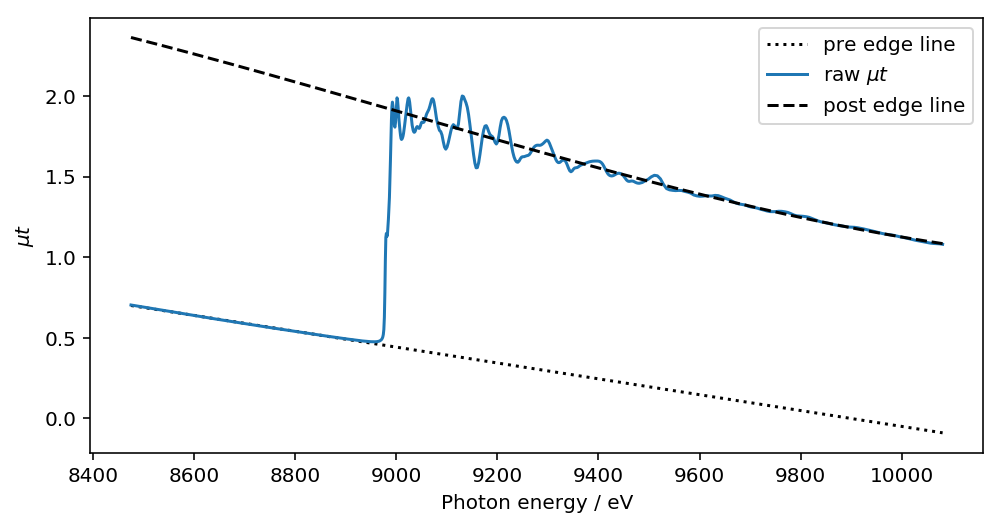
ここまでは特にバックグラウンド除去のパラメータを明示的に指定しませんでしたが、メソッドを実行する際に以下のパラメータを指定することで、所望の条件での処理が可能です。
| パラメータ名 | 説明 |
|---|---|
| energy | 1-d array of x-ray energies, in eV |
| mu | 1-d array of μ(E)μ(E) |
| group | output group |
| e0 | edge energy, E0 in eV. If None, it will be determined here. |
| step | edge jump. If None, it will be determined here. |
| pre1 | low E range (relative to E0) for pre-edge fit |
| pre2 | high E range (relative to E0) for pre-edge fit |
| nvict | energy exponent to use for pre-edge fit. See Note below. |
| norm1 | low E range (relative to E0) for post-edge fit |
| norm2 | high E range (relative to E0) for post-edge fit |
| nnorm | number of terms in polynomial (that is, 1+degree) for post-edge, normalization curve. Default=3 (quadratic) |
先ほどは引数に取ったGroup インスタンスに処理結果の数値データが格納されましたが、上記のgroup パラメータを指定することで、所望のGroup インスタンスに結果を出力することも可能です。例えば、これを利用すると、同一試料を複数の異なる条件で解析したいときに条件ごとにGroup を分けることいったことが出来ます。
今後のために、ここで明示的にパラメータを指定して、バックグラウンド除去および規格化をしなおしておきましょう。
lp.xafs.pre_edge(dat, e0=8985, pre1=-500, pre2=-30, norm1=150, norm2=900, nnorm=3, group=dat, _larch=session)
ちなみに、Athena がデフォルトでやっているように、post edge のバックグラウンドを規格化強度1.0 に合うように調整することも、自分でコードをちょっと書くことで可能になります。
これには、規格化因子であるedge_step を使います。たとえば、バックグラウンドを除去した後のpost edgeのバックグラウンドは以下のように計算でます。
fig = plt.figure(figsize=(8, 4))
post_edge_norm = (dat.post_edge - dat.pre_edge)/dat.edge_step
plt.plot(dat.energy, post_edge_norm , label="post-edge background")
plt.plot(dat.energy, dat.norm, label="normalized XAFS spectrum")
plt.xlabel("Photon energy / eV"); plt.ylabel("normalized $\mu t$"); plt.legend()
plt.show()
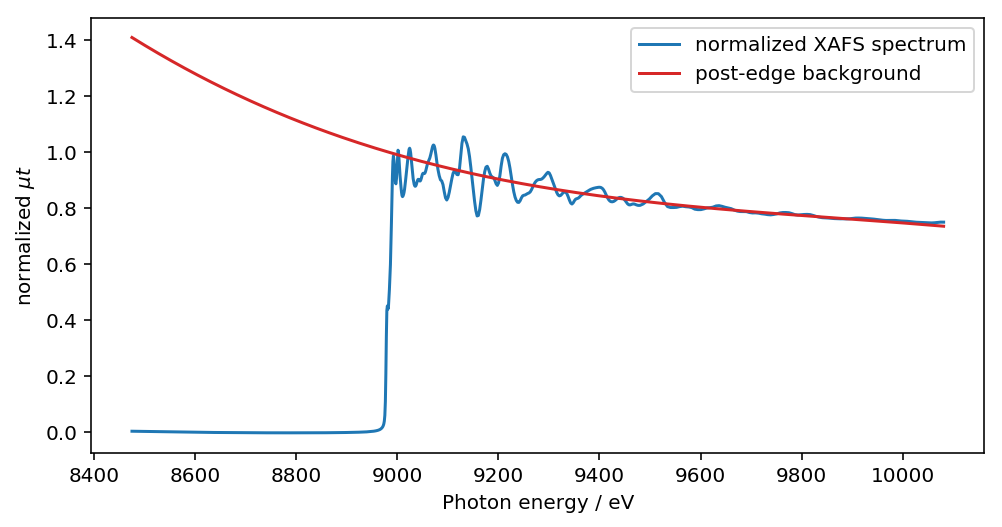
あとは、post edge 部に、1.0 とpost edge バックグラウンドの差分を足してやればOKです。
fig = plt.figure(figsize=(8, 4))
flattend_norm = np.copy(dat.norm)
flattend_norm[dat.energy > dat.e0] += (1.0 - post_edge_norm)[dat.energy > dat.e0]
plt.plot(dat.energy, dat.norm, label="just normalized")
plt.plot(dat.energy, flattend_norm, label="normalized & post-edge flattend")
plt.ylim(-0.05, 1.4)
plt.xlabel("Photon energy / eV"); plt.ylabel("normalized $\mu t$"); plt.legend(loc="upper right")
plt.show()
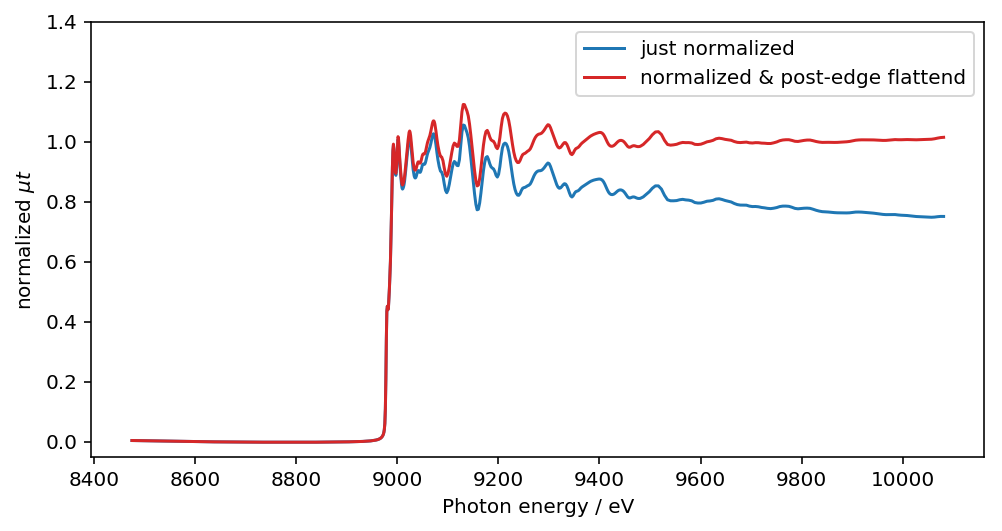
ATHENA で見慣れた形状の規格化XAFS スペクトルが見えていますね。
この処理は必須ではないし、規格化の仕方によってはXANES 領域のスペクトル形状を歪める可能性がありますが、Athena のマニュアルによればXANES の線形結合フィッティング解析等で、単に規格化したものよりも精度が向上するとかいう話もあるので、お好みで使うと良いでしょう。
EXAFS 振動の抽出
EXAFS 振動を抽出するには、XAFSスペクトルの振動の中心線を引く必要があります。これには、autobk という名前のアルゴリズムが広く利用されています。
larch では、アルゴリズム名称そのままのlarch_plugins.xafs.autobk メソッドを用いることにより、EXAFS 振動の抽出が可能です。このメソッドにも、pre_edge と同様に多くのパラメータが指定可能ですが、ここではバックグラウンドを見積もる範囲の下限と上限であるkmin とkmax のみを指定することにします。詳細は公式ドキュメントで確認してください。
lp.xafs.autobk(dat, kmin=0.0, kmax=16.5, _larch=session)
これによって、dat に属性k, chi が追加されます。それぞれ、光電子の波数とEXAFS 振動です。グラフに描いてみましょう。
fig = plt.figure(figsize=(8, 4))
plt.plot(dat.k, dat.chi)
plt.xlabel("Wavenumber of Photoelectron / $\mathrm{\AA}^{-1}$"); plt.ylabel("EXAFS oscillation $\chi(k)$")
plt.show()
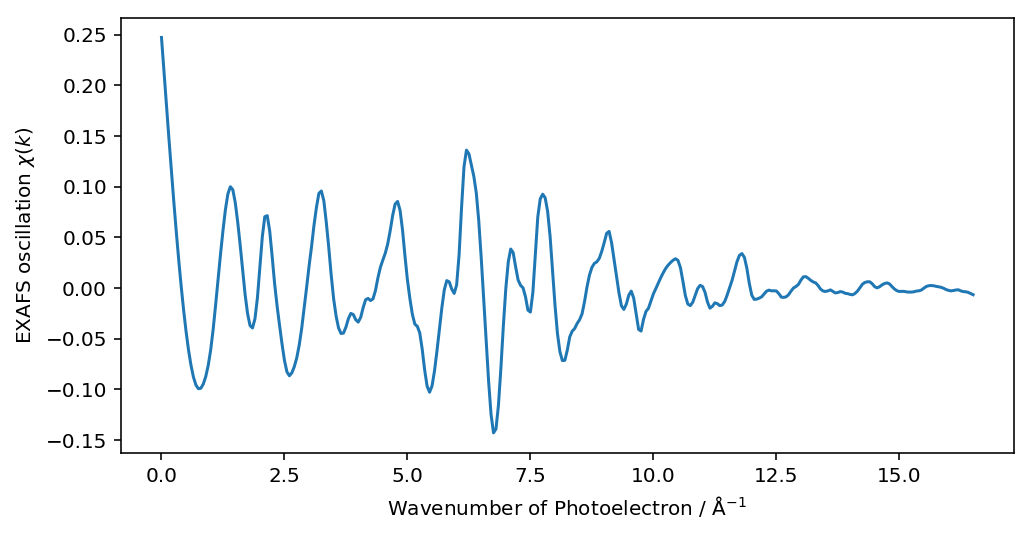
一般的にEXAFS では、高波数側を強調するために横軸であるk の累乗を乗じますが、(おそらく)そのためのメソッドは用意されておらず、また属性にも追加されないため、自ら計算する必要があります。
例えば、$k^2$ を乗じてみましょう。
fig = plt.figure(figsize=(8, 4))
plt.plot(dat.k, dat.k**2 * dat.chi)
plt.xlabel("Wavenumber of Photoelectron / $\mathrm{\AA}^{-1}$"); plt.ylabel("$k^2 \\times$ EXAFS oscillation $\chi (k)$ / $k^{-2}$")
plt.show()
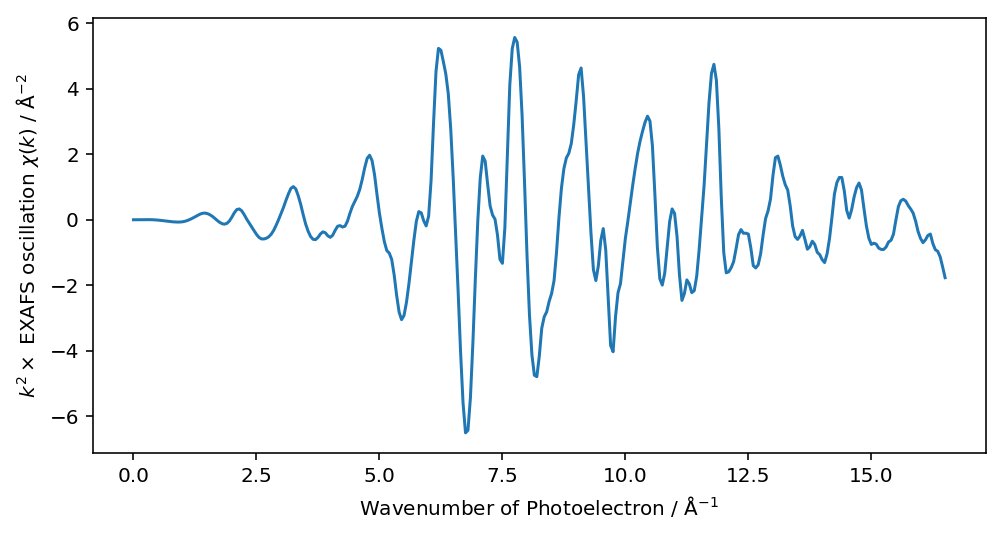
高波数側が協調されたEXAFS 振動が得られました。振動抽出もだいたい大丈夫そうですね。
ちなみに、pre_edge を実行する前にautobk を実行すると、自動でpre_edge を実行してくれるため、結果としてnorm 属性等が追加されます。ただし、メソッドの実行時にパラメータを指定しないと初期値での処理になるため、注意が必要です。
動径構造関数の導出
EXAFS 振動をフーリエ変換することで動径構造関数が得られますが、これにはlarch_plugins.xafs.xftf メソッドを使います。
パラメータとして$\chi(k)$ に乗ずる$k$ の累乗、フーリエ変換する$k$の範囲、窓関数の種類と幅等を指定しましょう。ここでは、$k^2$ を乗じて、$3 < k < 15$の範囲をフーリエ変換し、hanning の窓関数($dk=1.0$) を利用します。
lp.xafs.xftf(dat, kweight=2, kmin=3, kmax=15, dk=1.0, window="hanning", _larch=session)
動径構造関数、すなわちフーリエ変換の絶対値はchir_mag という属性としてGroup インスタンスに追加されます。また、その横軸である動径距離はr という属性に追加されます。
fig = plt.figure(figsize=(8, 4))
plt.plot(dat.r, dat.chir_mag, color="k")
plt.xlim(0, 6); plt.ylim(-0.1, 8)
plt.xlabel("Radial distance / $\mathrm{\AA}$")
plt.ylabel("Magnitude of Fourier Transform of $k^2 \cdot \chi$ / $k^{-3}$")
plt.show()
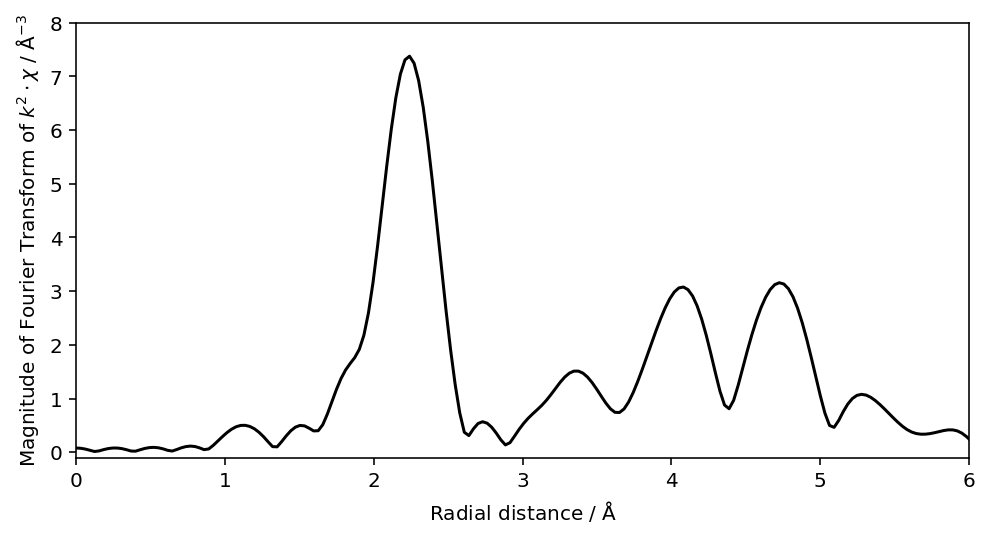
Cu の見慣れた動径構造関数が得られました。低温測定かつ高波数側まできれいにデータが取れているので、ピークが鋭くなってますね。
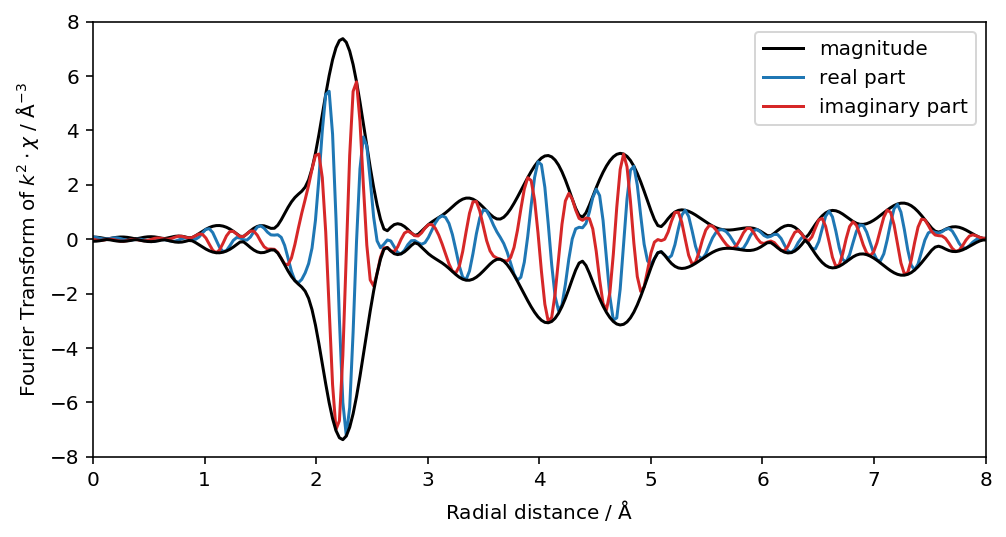
ちなみに、実部・虚部はそれぞれchir_re, chir_im に追加されます。これら単体ではあまり使わないかも知れませんが... 一応、envelope を描いてみましょう。
fig = plt.figure(figsize=(8, 4))
plt.plot(dat.r, dat.chir_mag, color="k", label="FT magnitude of $\chi(k)$")
plt.plot(dat.r, dat.chir_re, label="FT real part of $\chi(k)$")
plt.plot(dat.r, dat.chir_im, label="FT imaginary part of $\chi(k)$")
plt.plot(dat.r, -dat.chir_mag, color="k")
plt.xlabel( "Radial distance / $\mathrm{\AA}$"); plt.ylabel("Fourier Transform of $k^2 \cdot \chi$ / $k^{-3}$"); plt.legend(loc="upper right")
plt.show()
まとめ
Larch ライブラリを使用することで、Python でXAFS 解析ができることを確認しました。わりと簡単だということが分かってもらえたでしょうか。
ぶっちゃけデータ数が少なければATHENA を使ったほうが早いですが、たとえば微妙な測定結果でバックグラウンドの引き方を変えたときにどう変化するか確認したいときなど、パラメータを細かく広範囲に振るようなときには有用です。また、最近流行りのin situ/operando 測定の解析には威力を発揮します。(ATHENA は同時に読み込めるファイル数が20~30程度なので)
途中で面倒になったので書きませんでしたが、FEFF で計算した散乱パスを読み込んでEXAFS のフィッティングも可能で、最近のクソみたいに不安定なARTEMISよりも簡単にパラメータを振って系統的なフィッティング検討ができるので、興味のある方は公式ドキュメントを読んでみてください。
-
ちょっと前のバージョンで、import の仕方が変わったので注意が必要ですが、これから使う人は気にする必要はないです。 ↩