概要
Python からLarch を利用してXAFS 解析
https://qiita.com/inashiro/items/f1c10440618cf73a2d81
の続きです。
Larch には、強力なX 線関連のデータベース機能が備わっています。これは(たぶん)Demeter パッケージ内のHephaestus1 に対応するものです。データ自体は、SQLite で作られたX 線関連のデータベースであるXrayDB2 のものを利用しているようです。Python を用いてX 線関連手法の解析を行うときには、非常に役立つと思います。
この記事では、いくつかの機能を簡単に紹介します。全てを網羅しているわけではないので、適宜以下の公式ドキュメントを参照して頂ければと思います。
http://xraypy.github.io/xraylarch/xray/index.html
ライブラリの読み込み
Larch やnumpy, matplotlib は順序含めて以下のように読み込んであるものとします。Jupyter Notebook での利用を想定していて、Pythonのバージョンは2.7.14 です。3
from larch import Interpreter
import larch_plugins as lp
import numpy as np
import matplotlib.pyplot as plt
session = Interpreter()
%matplotlib inline
データベース機能
元素記号(atomic symbol)と原子番号(atomic number)
Larch では、元素記号もしくは原子番号からさまざまな数値を取得できます。まず手始めに、元素記号から原子番号を、原子番号から元素記号をそれぞれ取得してみましょう。
Cu_atomic_number = lp.xray.atomic_number('Cu', _larch=session)
Cu_atomic_symbol = lp.xray.atomic_symbol(Cu_atomic_number, _larch=session)
print "Atomic number of " + Cu_atomic_symbol + " : " + str(Cu_atomic_number)
Atomic number of Cu : 29
以下では、基本的には原子番号を使って物理量を取得していきます。
原子量(atomic mass)
原子量を取得できます。
lp.xray.atomic_mass(Cu_atomic_number, _larch=session)
63.546
吸収端(absorption edge)
原子番号と吸収端を指定することで、吸収端エネルギー、蛍光収率、エッジジャンプが取得できます。
lp.xray.xray_edge(Cu_atomic_number, 'K', _larch=session)
(8979.0, 0.441091, 7.56)
返り値のタプルの中身は、左から吸収端エネルギー(eV)、蛍光収率、エッジジャンプになっています。
特定の吸収端ではなく、存在する全ての吸収端のデータを返すメソッドも用意されています。
lp.xray.xray_edges(Cu_atomic_number, _larch=session)
{'K': (8979.0, 0.441091, 7.56),
'L1': (1096.7, 0.0016, 1.13303),
'L2': (952.3, 0.0057, 1.4),
'L3': (932.7, 0.011, 3.135),
'M1': (122.5, 4.1e-06, 1.04),
'M2': (77.3, 1.6e-05, 1.0),
'M3': (75.1, 0.0, 1.0),
'M4': (5.0, 0.00244687, 1.0),
'M5': (5.0, 0.0, 1.0)}
返り値はディクショナリとなり、キーには吸収端の名前が設定されます。異なる元素の情報を一度に得たい場合には、リスト内包表記を使うと良いでしょう。
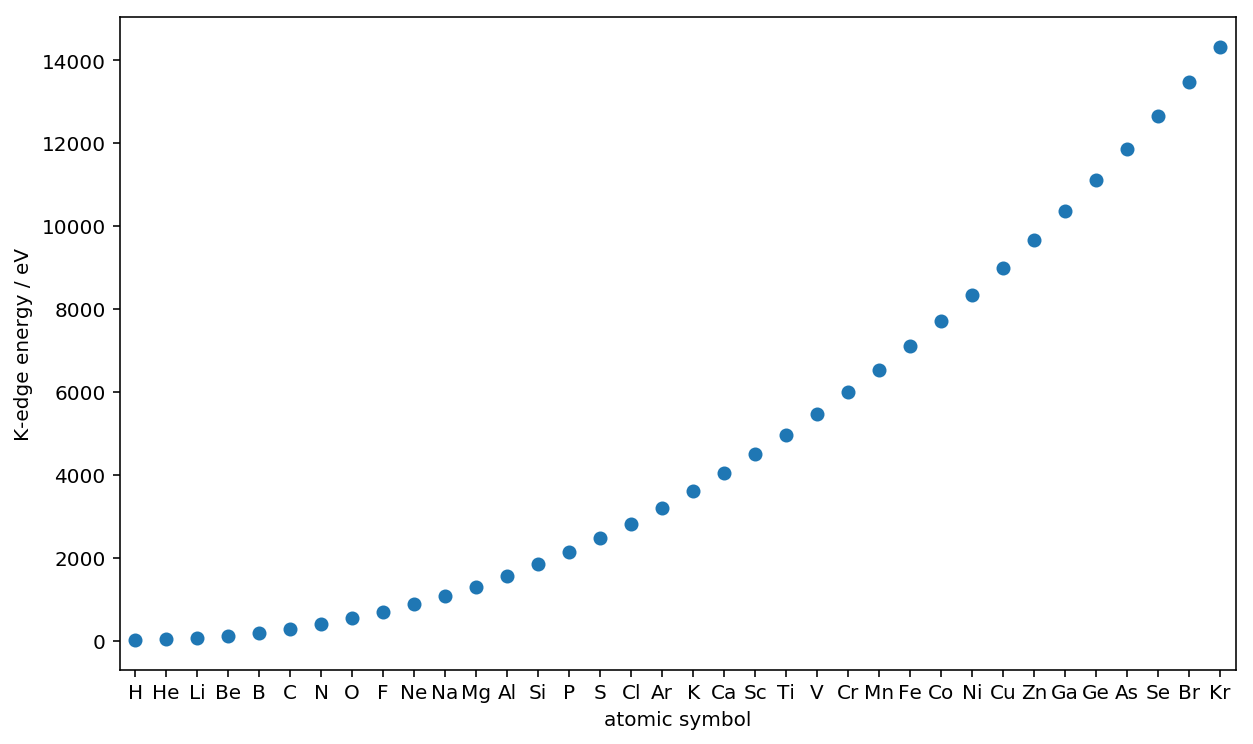
# atomic numbers
z_numbers = np.arange(1, 36+1, 1)
# atomic symbols and K-edge energies
symbols = [lp.xray.atomic_symbol(z, _larch=session) for z in z_numbers]
K_edge_energy = [lp.xray.xray_edge(z, 'K', _larch=session)[0] for z in z_numbers]
# plot
fig = plt.figure(figsize=(10, 6))
fig.patch.set_facecolor('white')
plt.plot(z_numbers, K_edge_energy, 'o')
plt.xticks(z_numbers, symbols, size=10)
plt.xlim(0.5, 36.5)
plt.xlabel("atomic symbol")
plt.ylabel("K-edge energy / eV")
plt.show()
蛍光X線(x-ray fluorescence)
吸収端と同様に、蛍光X線に関する情報を得ることができます。
lp.xray.xray_line(Cu_atomic_number, 'Ka1', _larch=session)
(8046.3, 0.577108, u'K', u'L3')
返り値のタプルの中身は、左から蛍光X線のエネルギー(eV)、強度、始状態、終状態になっています。始状態、終状態については、例えば今回だと$K\alpha_1$線は、$K$殻($1s$軌道) から$L_3$殻($2p_{2/3}$軌道) への励起状態に対応していることを示しています。
全ての蛍光X線のリストを同時に得ることもできます。
lp.xray.xray_lines(Cu_atomic_number, _larch=session)
{'Ka1': (8046.3, 0.577108, u'K', u'L3'),
'Ka2': (8026.7, 0.294269, u'K', u'L2'),
'Ka3': (7882.3, 0.000306271, u'K', u'L1'),
'Kb1': (8903.9, 0.0840096, u'K', u'M3'),
'Kb3': (8901.7, 0.043517, u'K', u'M2'),
'Kb5': (8974.0, 0.000789945, u'K', u'M4,5'),
'La1': (927.7, 0.840234, u'L3', u'M5'),
'La2': (927.7, 0.0924257, u'L3', u'M4'),
'Lb1': (947.3, 0.93381, u'L2', u'M4'),
'Lb3': (1021.6, 0.586166, u'L1', u'M3'),
'Lb4': (1019.4, 0.413833, u'L1', u'M2'),
'Ll': (810.2, 0.0673403, u'L3', u'M1'),
'Ln': (829.8, 0.06619, u'L2', u'M1')}
寿命幅 (lifetime width)
各元素・吸収端での内殻空孔の寿命幅 (eV) を取得できます。ただし、吸収端ごとに取得するメソッドは用意されておらず、まとめてディクショナリとしての取得になるようです。
lp.xray.core_width(Cu_atomic_number, _larch=session)
[(u'K', 1.7292),
(u'L1', 5.2801),
(u'L2', 1.1618),
(u'L3', 0.596),
(u'M1', 2.5259),
(u'M2', 1.6818),
(u'M3', 1.6818),
(u'M4', 0.033),
(u'M5', 0.033)]
これらは、Keski-Rahkonen とKrause のデータ4のようです。
原子散乱因子(atomic scattering factor)
異常分散項を含めた原子散乱因子$f$ は複素数であり、散乱角$\theta$、X線の波長$\lambda$ (Å) を用いて
$$
f = f_0\left( \frac{\sin \theta}{\lambda}\right) + f' + if''
$$
と書けます。Larch では、これら$f_0, f', f''$ のすべてを計算することができます。
まず、$f_0$ を計算してみましょう。$f_0$ はイオン種によって値が変わるため、原子番号による指定はできません。ここでは、0価(金属)の銅の値を計算してみましょう。また、$f_0$ は$\sin \theta / \lambda$ の関数なので、その値も与えてやる必要があります。今回は、$\sin \theta / \lambda=1.0$とします。
lp.xray.f0('Cu', 1.0, _larch=session)
array([ 7.16119319])
返り値はndarray になります。$\sin \theta / \lambda$ にndarray を指定することもできます。以下で、異なる価数のバナジウムの$f_0$ を計算してみます。5
q = np.arange(0, 2, 0.01)
V = lp.xray.f0('V', q, _larch=session)
V2 = lp.xray.f0('V2+', q, _larch=session)
V3 = lp.xray.f0('V3+', q, _larch=session)
V5 = lp.xray.f0('V5+', q, _larch=session)
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111)
ax.plot(q, V, label="V")
ax.plot(q, V2, label="V2+")
ax.plot(q, V3, label="V3+")
ax.plot(q, V5, label="V5+")
ax.set_xlim(0, 2.0)
ax.set_ylim(0, 24)
ax.text(0.05, 22.5, 'V', size=12)
ax.annotate('V$^{2+}$',
xy=(0.05, 20.6), xycoords='data',
xytext=(30, 20), textcoords='offset points', size=12,
arrowprops=dict(arrowstyle="-"))
ax.annotate('V$^{3+}$',
xy=(0.06, 19.5), xycoords='data',
xytext=(35, 10), textcoords='offset points', size=12,
arrowprops=dict(arrowstyle="-"))
ax.text(0.03, 16, 'V$^{5+}$', size=12)
ax.set_xlabel("$\sin\\theta / \lambda$ / $\mathrm{\AA}^{-1}$", size=12)
ax.set_ylabel("$f_0$", size=12)
plt.show()

$f'$, $f''$ はChantler によるデータ6を利用できます。ここでは、Ni について計算してみます。7
適当なエネルギーを与えても内挿して計算してくれるようですが、xrayDBインスタンスのメソッドであるchantler_energies を使うことでテーブル値に対応するエネルギーが得られ、より厳密に値が求まるようです。
xray_database = lp.xray.xrayDB()
energy = xray_database.chantler_energies('Ni', emin=12398.4/3.2, emax=12398.4/0.4)
wavelength = 12398.4/energy
f1 = lp.xray.f1_chantler('Ni', energy, _larch=session)
f2 = lp.xray.f2_chantler('Ni', energy, _larch=session)
fig = plt.figure(figsize=(10, 5))
plt.plot(wavelength, f1, label='$f\'$')
plt.plot(wavelength, f2, label='$f\'\'$')
plt.ylim(-15, 6)
plt.xlim(0.4, 3.2)
plt.xlabel("X-ray wavelength / $\mathrm{\AA}^{-1}$")
plt.ylabel("Dispersion correction")
plt.legend()
plt.show()

質量吸収係数(mass attenuation coefficient)
質量吸収係数$\mu_M$ (cm2/g) は、Chantler 6 もしくはElamら8 によるデータを利用できます。**Elam らによるデータの方がデフォルト扱いのようです。**先ほどと同様に、Ni について計算してみましょう。7
xray_database = lp.xray.xrayDB()
energy = xray_database.chantler_energies('Ni', emin=12398.4/3.2, emax=12398.4/0.4)
wavelength = 12398.4/energy
muM_Chantler = lp.xray.mu_chantler('Ni', energy, _larch=session)
muM_Elam = lp.xray.mu_elam('Ni', energy, _larch=session)
fig = plt.figure(figsize=(10, 5))
plt.plot(wavelength, muM_Chantler, label="Chantler")
plt.plot(wavelength, muM_Elam, label="Elam et al.")
plt.xlabel("X-ray wavelength / $\mathrm{\AA}^{-1}$")
plt.ylabel("$\mu_M$ / cm$^2$g$^{-1}$")
plt.xlim(0.4, 3.2)
plt.ylim(0, 400)
plt.legend()
plt.show()

長波長側で少し値がずれているようです。
Elamのデータでは、光電吸収やコンプトン散乱による寄与のみを出力することもできます。
energy = np.logspace(1, 5.9, 1000)
muM_total = lp.xray.mu_elam('Ni', energy, kind='total', _larch=session)
muM_photo = lp.xray.mu_elam('Ni', energy, kind='photo', _larch=session)
muM_coh = lp.xray.mu_elam('Ni', energy, kind='coh', _larch=session)
muM_incoh = lp.xray.mu_elam('Ni', energy, kind='incoh', _larch=session)
fig = plt.figure(figsize=(10, 5))
plt.loglog(energy/1000, muM_total, label="Total absorption")
plt.loglog(energy/1000, muM_photo, label="Photoelectric absorption")
plt.loglog(energy/1000, muM_coh, label="Coherent scattering cross section")
plt.loglog(energy/1000, muM_incoh, label="Incoherent scattering cross section")
plt.xlabel("Photon energy / keV")
plt.ylabel("absorption coefficient / cm$^2$g$^{-1}$")
plt.legend()
plt.show()

良く放射線関連の教科書に書いてある通り、高エネルギーで全吸収と光電吸収で差が生じることが分かります。
線吸収係数(linear attenuation coefficient)
典型的な物質名や組成式、密度等を引数として、線吸収係数$\mu$ (1/cm) を計算するメソッドが用意されています。
まず、物質名や組成式を扱うメソッドについて、見てみましょう。ライブラリに登録されている物質名から組成式と密度を出力するには、以下のようにします。ここでは、カプトンのデータを取得します。
lp.xray.material_get('kapton', _larch=session)
('C22H10N2O5', 1.43)
タプルの第一要素は組成式で、第二要素は密度(g/cm3)です。
また、データベースに未登録の物質に対応するために、組成式をパースするメソッドが用意されています。カプトン(ポリイミド)の組成式を与えてみます。
lp.xray.chemparse('C22H10N2O5')
{'C': 22.0, 'H': 10.0, 'N': 2.0, 'O': 5.0}
結果としてディクショナリが返ってきて、キーに元素名が、値に各元素の組成比が入ります。
Larch では、これらのメソッドと、Elamらの$\mu_M$ を用いて化合物の線吸収係数$\mu$ を計算するmaterial_mu メソッドが用意されています。material_mu は物質名か組成式を引数に取ることができます。たとえば、第一引数に物質名を指定した場合、与えられたエネルギー(eV) での線吸収係数を計算するには、以下のようにします。
lp.xray.material_mu('kapton', 10*1e3, _larch=session)
4.5473835722022518
線吸収係数の計算には密度が必要ですが、物質名で指定した場合は、登録された密度(material_getで得られる値)を用いるようです。
一方、登録されていない物質の組成式を第一引数に指定する場合は、密度(g/cm3) を明示してやる必要があります。(登録されている物質と組成式が一致した場合はその値を使用するようです。) たとえば、カプトンの組成式を与えてやると、
lp.xray.material_mu('C22H10N2O5', 10*1e3, _larch=session)
4.5473835722022518
このように密度を明示しなくても計算が可能です。一方、データベースに登録されていない例としてLiCoO2 という物質について計算してみます。
lp.xray.material_mu('LiCoO2', 10*1e3, density=5.16, _larch=session)
582.3455865101015
LiCoO2 の場合、density を明示しないとエラーになります。
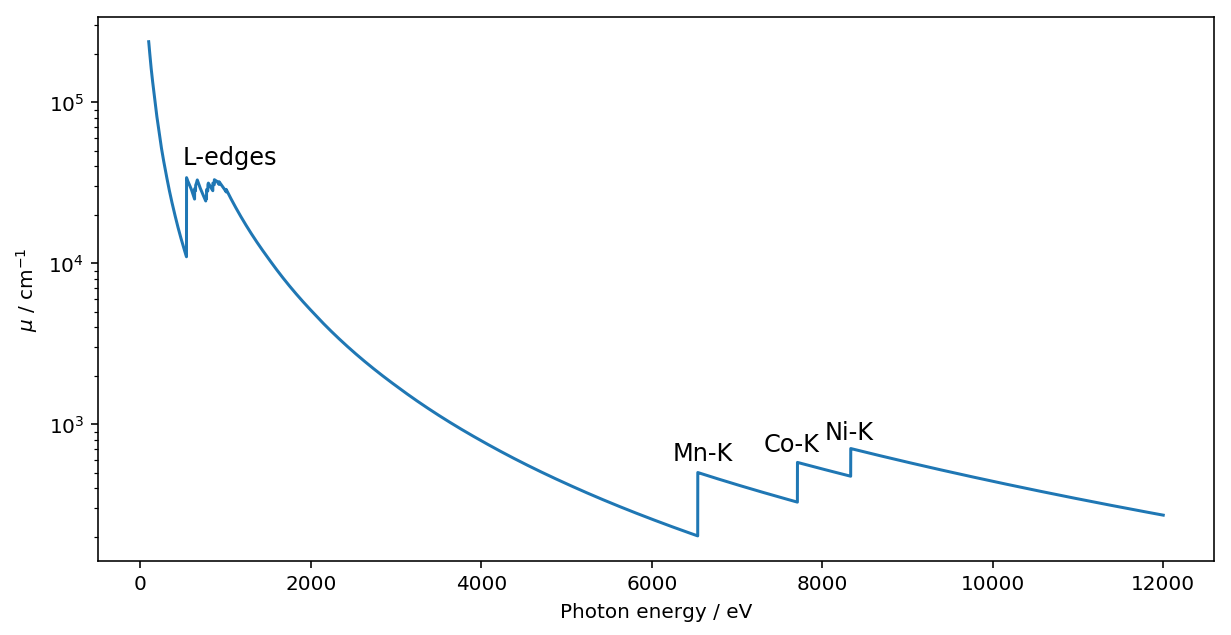
ここまでのメソッドと同様に、material_mu でもエネルギーにndarray を与えることができます。いくつか吸収端が見える例として、LiNi1/3Mn1/3Co1/3O3 を例として計算してみます。(以下では、密度には適当な数字を与えています。)
energy = np.arange(100, 12000, 1)
NCM_mu = lp.xray.material_mu('LiNi0.333Co0.333Mn0.333O2', energy, density=4.0, _larch=session)
fig = plt.figure(figsize=(10, 5))
plt.semilogy(energy, NCM_mu)
plt.text(500, 31404+10000, 'L-edges', size=12)
plt.text(6539-300, 502+100, 'Mn-K', size=12)
plt.text(7709-400, 579+100, 'Co-K', size=12)
plt.text(8333-300, 707+100, 'Ni-K', size=12)
plt.xlabel("Photon energy / eV")
plt.ylabel("$\mu$ / cm$^{-1}$")
plt.show()
まとめ
Larch のデータベース機能は、XAFS のみならずXRD 等の他手法にも活用できるものと思います。実験前のちょっとした検討にも使えることが多いので、ぜひ試してみてください。
-
ちょっと前まではpython 3 では未だバグがあるかも... という文言が公式サイトにあったんですが、最近3 系でのチェックが進んできたようで2.7 系のサポートを外すスケジュールを検討しているとの記載になっています。自分は3 系の環境構築がきちんと出来てないので、ひとまず2.7 系で使っています。 ↩
-
O.Keski-Rahkonen and M.O.Krause, Atomic Data and Nuclear Data Tables 14, 139 (1974) ↩
-
RIETAN-FP manual リスペクト。 ↩
-
W.T.Elam, B.D.Ravel and J.R.Sieber, Radiat. Phys. Chem. 63, 121 (2002) ↩