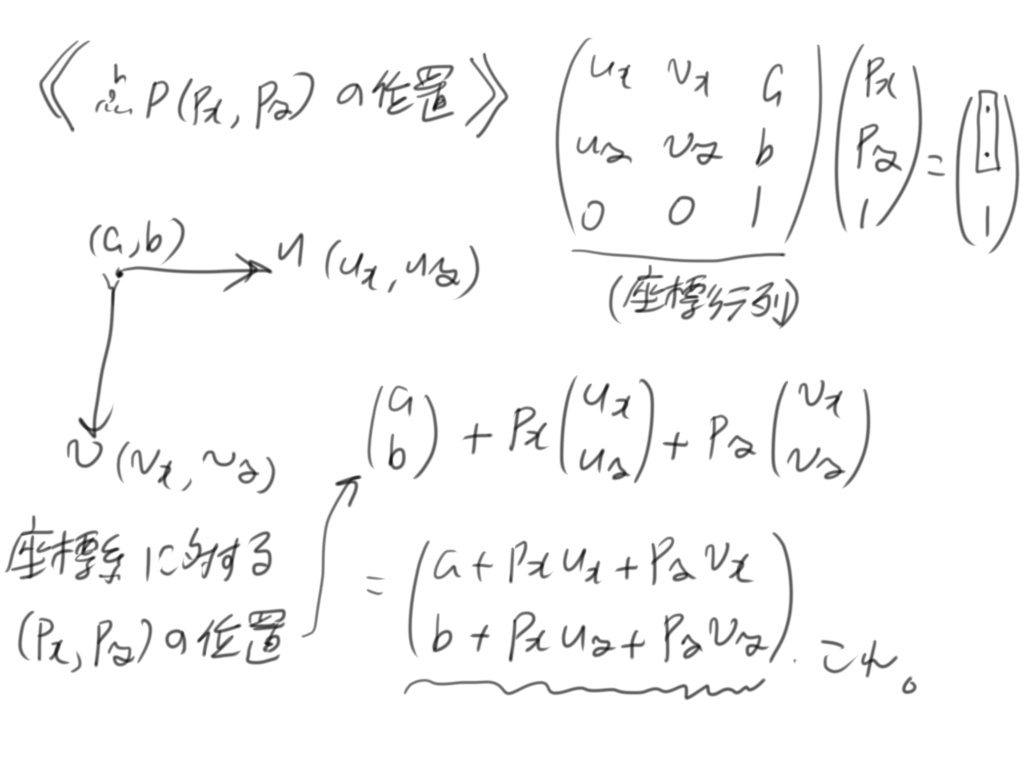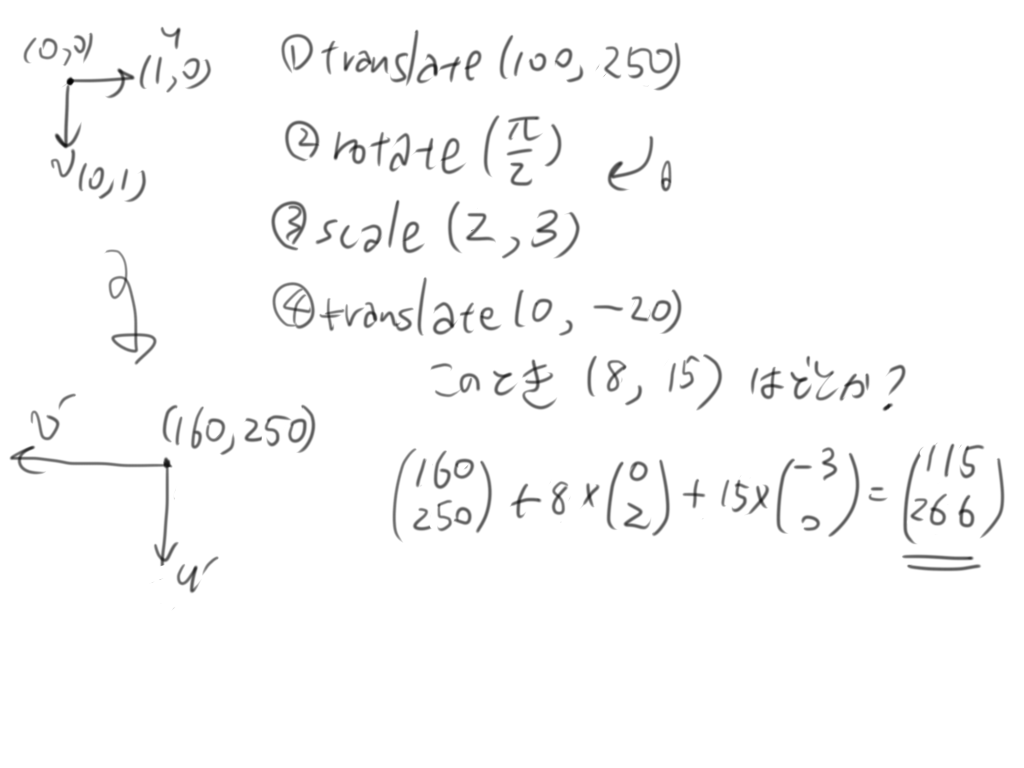はじめに
canvas2Dの線形変換には、平行移動、回転、拡縮があります。それが何をしているのかをざっくりと理解します。
座標系:基底と原点
まずデフォルトでは原点は(0,0)の位置にあります。基底のベクトルを$u,v$とします。$u$は(1,0)で、$v$は(0,1)がデフォルトです。このとき点(2,4)はどこでしょうか。
答えは(2,4)です。
なぜかというと図にある計算の通りです。これを線形結合と言います。成分ごとに係数を掛けて足し算をします。
一般の場合
原点と基底ベクトルが一般の場合は次のように計算します。
これが座標系に対する点の位置の計算方法です、行列で表すこともできます。
座標変換の関数であるtranslate,rotate,scaleというのは、この座標系を操作するための関数です。
今からその概要を説明します。
うるさい。
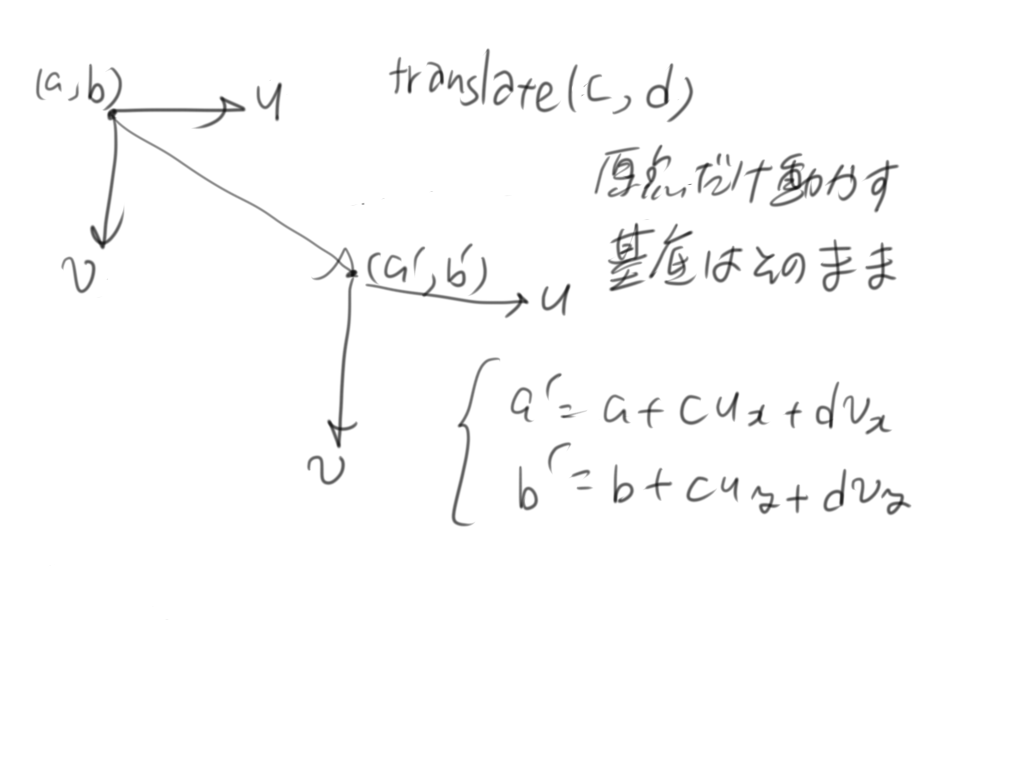
translate
translate(平行移動)は座標軸である基底を不変にし、原点のみ指定した値だけ動かすんですが、その動かし方は基底に依存します。すなわち(c,d)とある場合、単純にc,dを足すのではなく、$u$の$c$倍と$v$の$d$倍を順に(まあ順はどうでもいいんですが)足します。基底に依存するところがポイントですね。
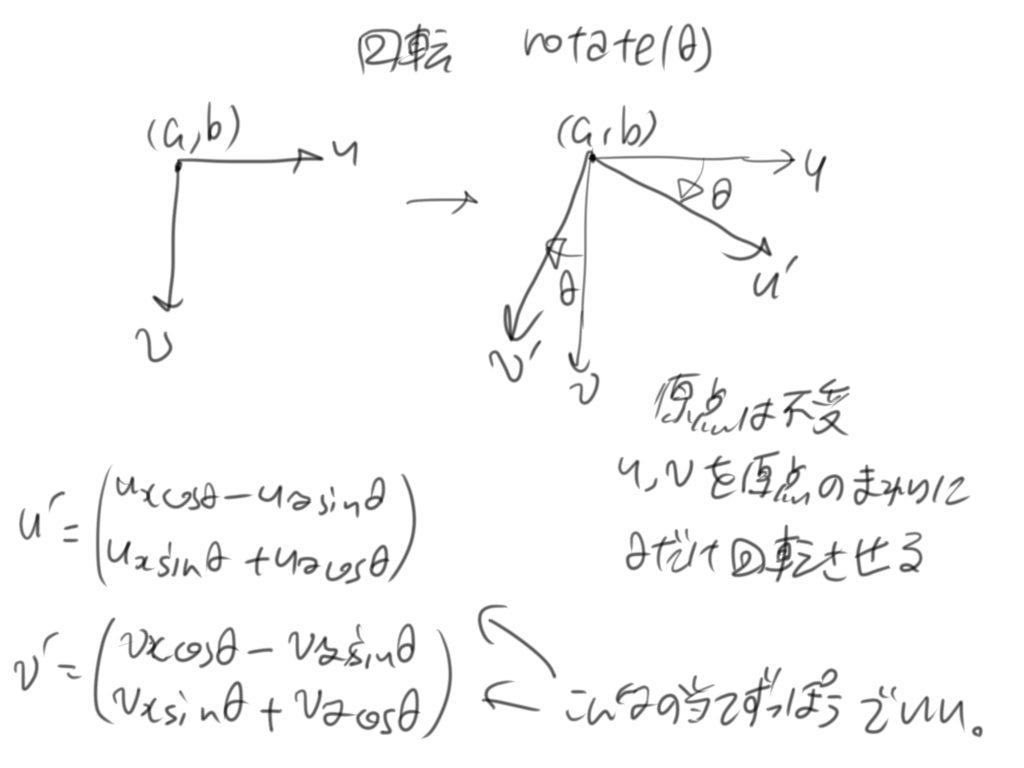
rotate
次にrotateは、原点を不変にし、基底のみ変更します。どう変更するかというと、回転させます。回転方向は今$y$軸が下向き(一般的なcanvas2Dの座標系)なので時計回りです。ざっくりいうとこんな感じの計算結果になります。ちなみに筆者はこんなのまじめに覚えていません。なんとなくコサインとサインの足し算掛け算の結果だな~って思いながら符号だけ帳尻合わせてます。要はサインシータの±についてどっちがどっちって話なんですが、まあPI/2の挙動からなんとなくわかるので、それでいいですね。これを理屈で理解するのは大変ですし、理解してもあんま面白くないので。
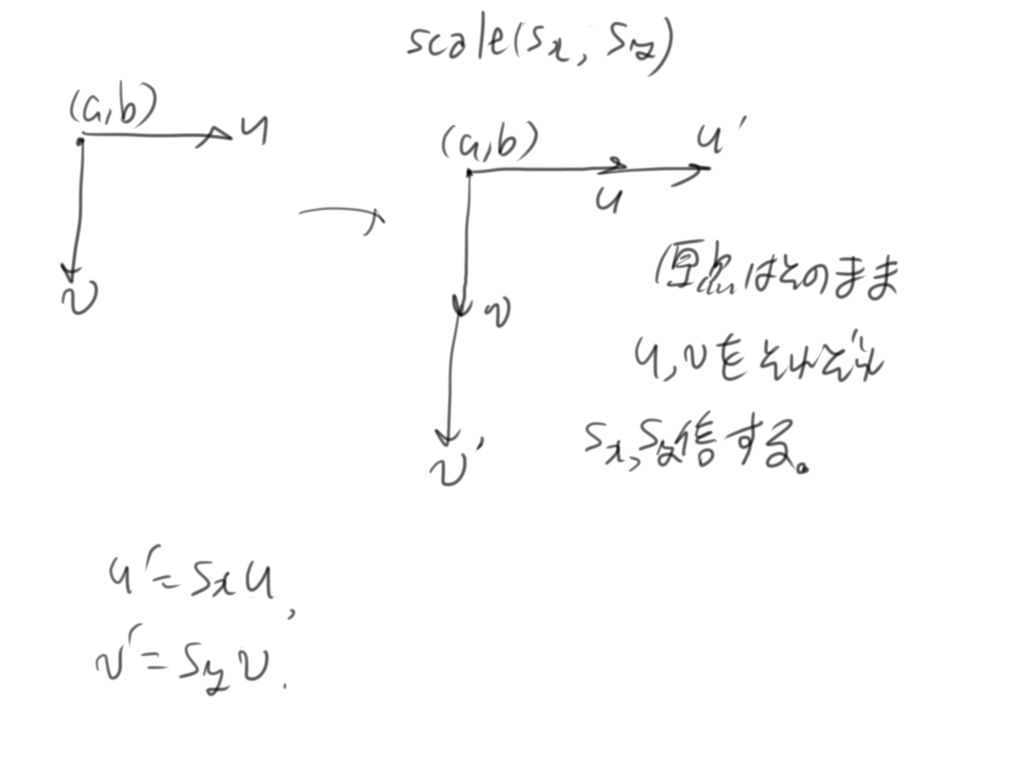
scale
最後にscaleは、原点を不変にし、基底のみ変更します。$(s_x,s_y)$だとして、$u$を$s_x$倍し、$v$を$s_y$倍します。基底のそれぞれに倍数を掛けるだけ。単純ですね。
練習
これらを踏まえたうえで、練習をします。
この順でtranslate,rotate,scale,translateを実行した場合、座標系はどうなるのか?そしてその結果、点(8,15)はどこになるのか?
答えは原点が(160,250)で、$u$は(0,2)で、$v$は(-3,0)で、位置は(115,266)です。実際...
const ctx = cvs.getContext("2d");
ctx.fillStyle = "black";
ctx.fillRect(0,0,400,400);
ctx.fillStyle = "white";
ctx.translate(100,250);
ctx.rotate(Math.PI/2);
ctx.scale(2,3);
ctx.translate(0, -20);
ctx.beginPath();
ctx.ellipse(8,15,8,8,0,0,Math.PI*2);
ctx.fill();
// transform解除
ctx.setTransform(1,0,0,1,0,0);
ctx.fillStyle = "blue";
ctx.beginPath();
ctx.ellipse(115, 266, 8,8,0,0,Math.PI*2);
ctx.fill();
この通り:
2つの円が重なりました。なお楕円の描画はスケール変換の影響を受けるので、原点の位置は同じなんですが大きさが変わっています。今は位置を確かめたいだけなので、これでいいですね。
おわりに
ちなみにp5ではpixelDensityを考慮して、devicePixelRatioが大きい場合にはデフォルトでscaleを実行しています。通常より大きいキャンバス上で描画しても違和感が無いように工夫しているわけです。レファレンスのどこにも書いてませんが、裏で色々やってるんですね。
ここまでお読みいただいてありがとうございました。