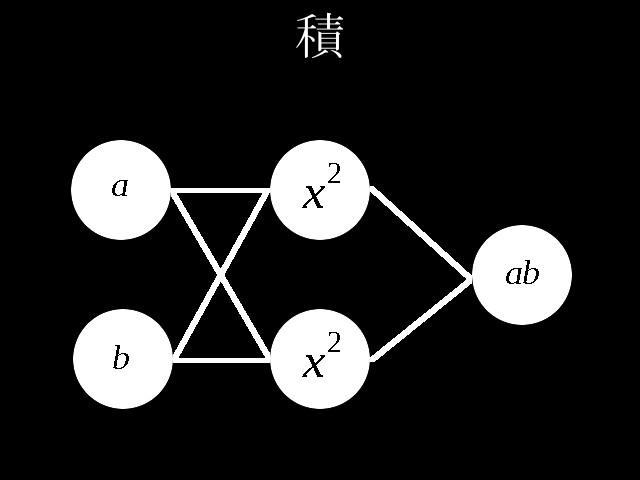
Qiita民が大好きなPythonで積のパーセプトロンを作成しました。
# coding=utf-8
import numpy as np
import matplotlib.pyplot as plt
# 初期値
# 学習回数
N = 500
# 層
layer = [2, 2, 1]
# バイアス
# bias = [0.0, 0.0]
# 学習率
η = [1.0, 1.0]
# 中間層数
H = len(η) - 1
# 教師値
mul = [None for _ in range(N)]
# 関数出力値
f_out = [[None for _ in range(H + 1)] for _ in range(N)]
# 関数入力値
f_in = [[None for _ in range(H + 1)] for _ in range(N)]
# 重み
w = [[None for _ in range(H + 1)] for _ in range(N + 1)]
for h in range(H + 1):
w[0][h] = np.random.uniform(-1, 1, (layer[h + 1], layer[h]))
print(w[0])
# 二乗誤差
dE = [None for _ in range(N)]
# ∂E/∂IN
δ = [[None for _ in range(H + 1)] for _ in range(N)]
# 学習
for n in range(N):
#入力値
f_out[n][0] = np.random.uniform(-1, 1, ((layer[0]), 1))
#教師値
mul[n] = f_out[n][0][0] * f_out[n][0][1]
#順伝播
f_in[n][0] = np.dot(w[n][0], f_out[n][0])
f_out[n][1] = f_in[n][0] * f_in[n][0]
#出力値
f_in[n][1] = np.dot(w[n][1], f_out[n][1])
#二乗誤差
dE[n] = f_in[n][1] - mul[n]#計算省略のため二乗誤差微分後の値
#逆伝播
δ[n][1] = 1.0 * dE[n]
δ[n][0] = 2.0 * f_in[n][0] * w[n][1].T * δ[n][1]
for h in range(H + 1):
w[n + 1][h] = w[n][h] - η[h] * f_out[n][h].T * δ[n][h]
# 出力
# 値
# 重み
print(w[N])
# 図
# 重み
# 領域縦
py = np.amax(layer)
# 領域横
px = (H + 1) * 2
# 領域寸法
plt.figure(figsize = (16, 9))
# 図横軸
x = np.arange(0, N + 1, 1) #0からN+1まで1刻み
# 描画
for h in range(H + 1):
for l in range(layer[h + 1]):
#領域座標
plt.subplot(py, px, px * l + h * 2 + 1)
for m in range(layer[h]):
#線
plt.plot(x, np.array([w[n][h][l, m] for n in range(N + 1)]), label = "w[" + str(h) + "][" + str(l) + "," + str(m) + "]")
#格子線
plt.grid(True)
#凡例
plt.legend(bbox_to_anchor = (1, 1), loc = 'upper left', borderaxespad = 0, fontsize = 10)
# 保存
plt.savefig('graph_mul.png')
# 図示
plt.show()
なお、重みについてですが今までは
w[0]=
\begin{pmatrix}
1 & 1\\
1 & -1
\end{pmatrix}
,w[1]=
\begin{pmatrix}
0.25 & -0.25
\end{pmatrix}
を目標値としていたのですが、改めて計算してみましたところ
w[0]=
\begin{pmatrix}
△ & □\\
▲ & ■
\end{pmatrix}
,w[1]=
\begin{pmatrix}
○ & ●
\end{pmatrix}\\
\\
入力値とw[0]の積\\
w[0]
\begin{pmatrix}
a\\
b
\end{pmatrix}
=
\begin{pmatrix}
△ & □\\
▲ & ■
\end{pmatrix}
\begin{pmatrix}
a\\
b
\end{pmatrix}
=
\begin{pmatrix}
△a + □b\\
▲a + ■b
\end{pmatrix}\\
\\
第1層に入力\\
\begin{pmatrix}
(△a + □b)^2\\
(▲a + ■b)^2
\end{pmatrix}\\
\\
第1層出力とw[1]の積=出力値\\
\begin{align}
&
w[1]
\begin{pmatrix}
(△a + □b)^2\\
(▲a + ■b)^2
\end{pmatrix}\\
=&
\begin{pmatrix}
○ & ●
\end{pmatrix}
\begin{pmatrix}
(△a + □b)^2\\
(▲a + ■b)^2
\end{pmatrix}\\
=&〇(△a + □b)^2 + ●(▲a + ■b)^2\\
=&\quad (○△^2 + ●▲^2)a^2\\
&+(○□^2 + ●■^2)b^2\\\
&+(2〇△□+2●▲■)ab
\end{align}\\
\\
なんだか、ややこしくなってしまってますが\\
とりあえずは、下記条件を満たせば積abを出力することができます。\\
\left\{
\begin{array}{l}
○△^2 + ●▲^2=0 \\
○□^2 + ●■^2=0 \\
2〇△□+2●▲■=1
\end{array}
\right.
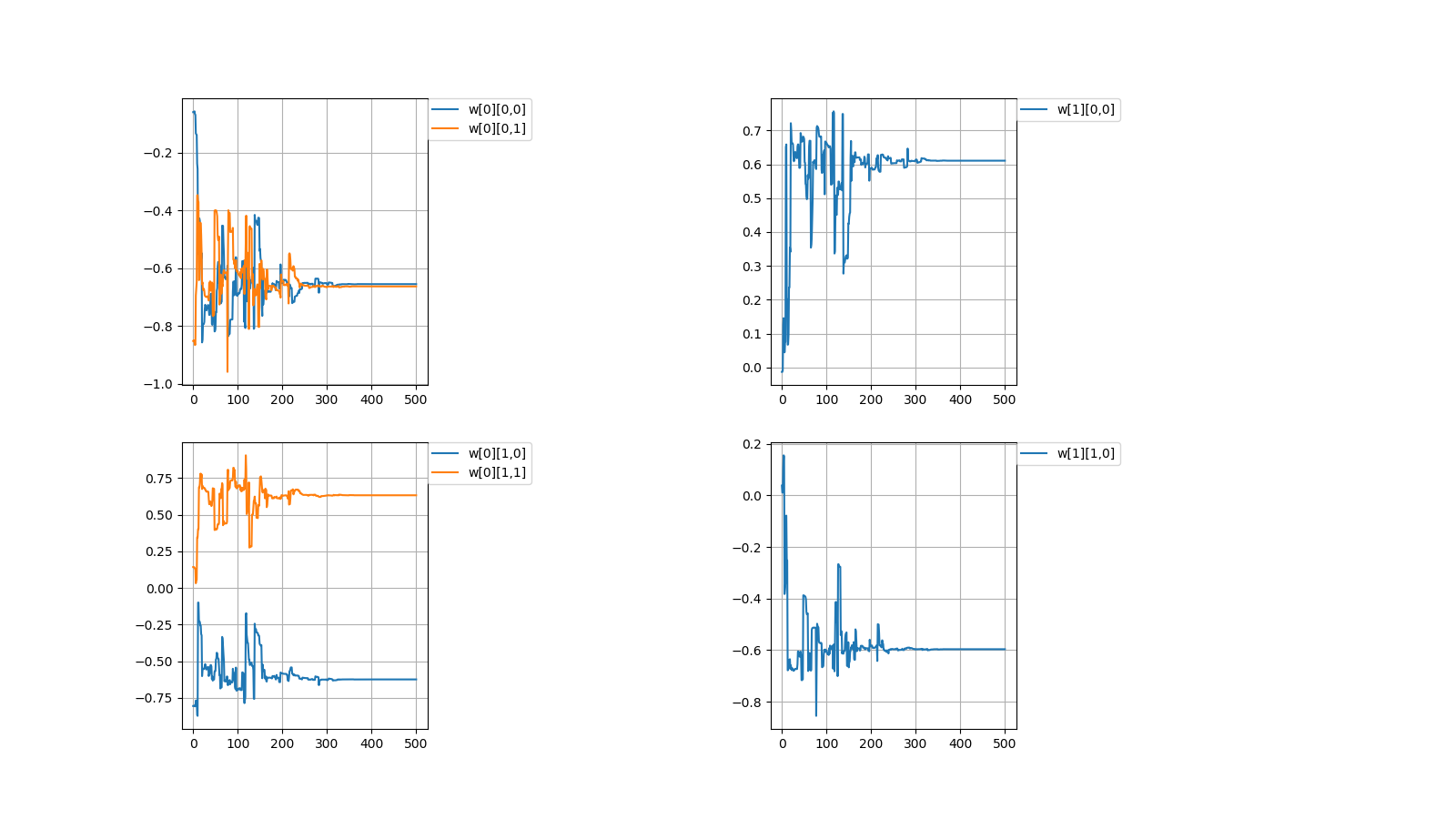
毎度恒例、初期値を乱数(-1.0~1.0)で決めてから学習を繰り返すと目標値に収束するか試してみました。
結論から言いますと、成功しました。
目標値\\
w[0]=
\begin{pmatrix}
△ & □\\
▲ & ■
\end{pmatrix}
,w[1]=
\begin{pmatrix}
○ & ●
\end{pmatrix}\\
\left\{
\begin{array}{l}
○△^2 + ●▲^2=0 \\
○□^2 + ●■^2=0 \\
2〇△□+2●▲■=1
\end{array}
\right.\\
\\
初期値\\
w[0]=
\begin{pmatrix}
-0.06001642 & -0.80560397\\
-0.85252436 & 0.14216594
\end{pmatrix}
,w[1]=
\begin{pmatrix}
-0.01316071 & 0.03798114
\end{pmatrix}\\
\left\{
\begin{array}{l}
○△^2 + ●▲^2=0.0275572039 \\
○□^2 + ●■^2=-0.0077736286 \\
2〇△□+2●▲■=-0.0104792494
\end{array}
\right.\\
\\
計算値\\
w[0]=
\begin{pmatrix}
-0.65548785 & -0.62435684\\
-0.66341526 & 0.63186139
\end{pmatrix}
,w[1]=
\begin{pmatrix}
0.61080948 & -0.59638741
\end{pmatrix}\\
\left\{
\begin{array}{l}
○△^2 + ●▲^2=-3.88711177092826E-5 \\
○□^2 + ●■^2=-3.21915003292927E-7 \\
2〇△□+2●▲■=0.9999528147
\end{array}
\right.
C#でやってた事と変わらないはずなのですが
Pythonでコードを書いたらうまく行ってしまいました。(C#にバグがあったかも。。。。)
拍子抜けです。
しかし、実は課題を抱えています。
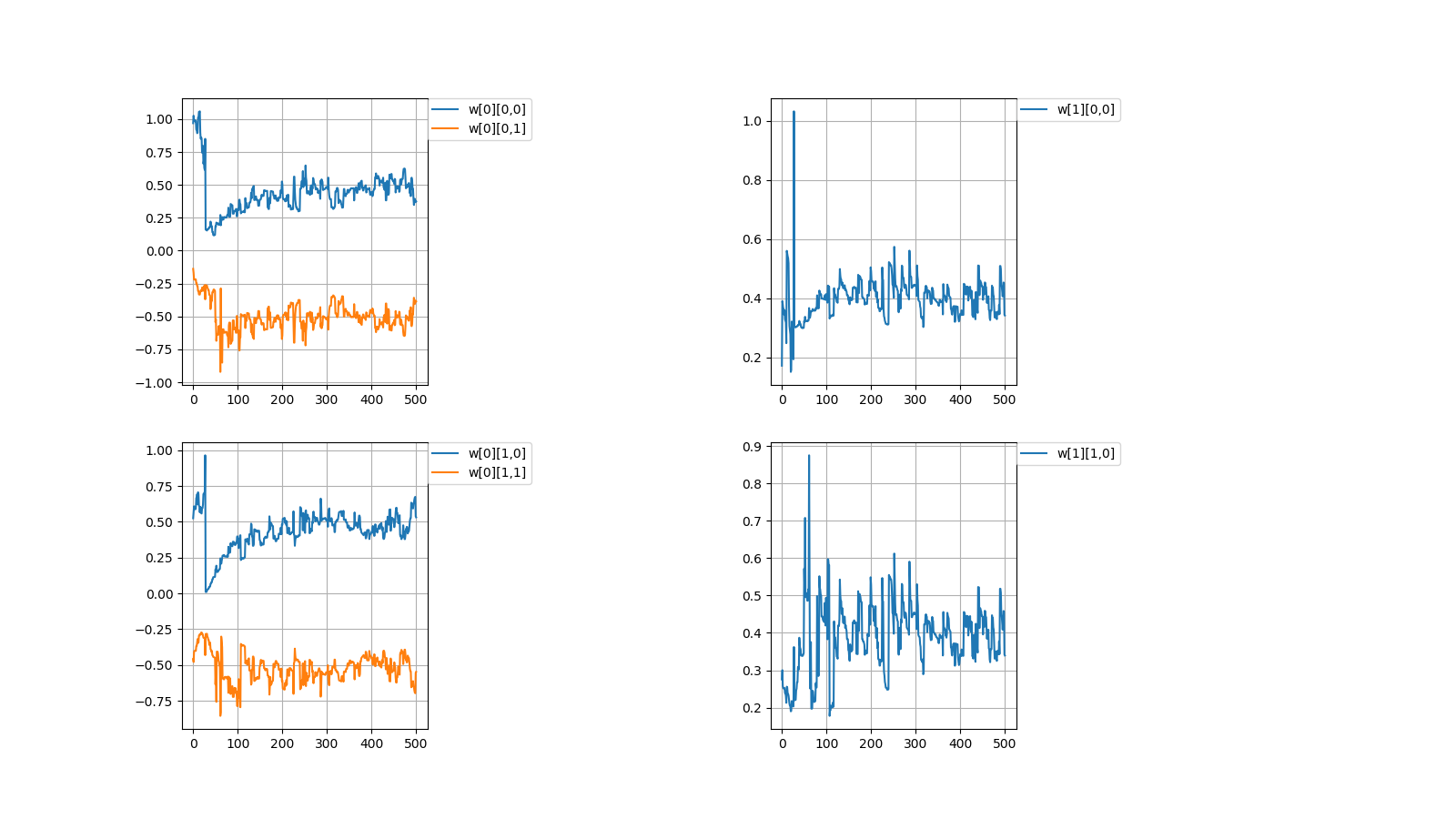
1,収束する時と収束しない時がある
初期値\\
w[0]=
\begin{pmatrix}
0.96898039 & 0.5250381\\
-0.13805777 & -0.457846
\end{pmatrix}
,w[1]=
\begin{pmatrix}
0.17181768 & 0.27522847
\end{pmatrix}\\
計算値\\
w[0]=
\begin{pmatrix}
0.37373305 & 0.53163593\\
-0.38455151 & -0.54773647
\end{pmatrix}
,w[1]=
\begin{pmatrix}
0.34178043 & 0.33940928
\end{pmatrix}\\
上記のように値が収束しない場合がときたまあります。
本当はプログラムを組んで収束しない時の統計を出すべきなんでしょうが
そこまでの気力がありませんでした。
2,重みの初期値と入力値が整数(-10~10)などの時は絶対に収束しない
3回学習させたぐらいで重みがオーバーフローしてしまいます。
(学習率を低くすればいいのだと後々気づきました。)
3,収束したらしたでいつも同じぐらいの値で収束する
どういう訳か、例えばw[0][0,0]=±0.6....ぐらいの値に落ち着く事がほとんどです。
一見、簡単そうなパーセプトロンでも謎が多いです。
次回
商