これなに?
バイオ系の学生が機械学習がしたいなあということで勉強をはじめました。
勉強ついでにまとめていけたらなあと思っています。
線形回帰
以下のような回帰式を用いて説明変数の値から目的変数を予測するモデル。
$$y=b_1x_1+b_2x_2+b_3x_3+...b_kx_k+e$$
$$y:目的変数$$
$$b_n: 編回帰変数$$
$$x_n:説明変数$$
$$e:誤差$$
scikit-learnの線形回帰を行うクラス
sklearn.linear_model.LinearRegressio
sklearn.linear_model.LinearRegressionクラスのアトリビュート
| attribute | |
|---|---|
| coef_ | 編回帰係数 |
| intercept_ | 切片 |
sklearn.linear_model.LinearRegressionクラスのmethod
| method | |
|---|---|
| fit(X, y[,sample_weight] | 線形回帰モデルのあてはめ |
| get_params([deep]) | パラメーターを取得 |
| predict(X) | 作成したモデルを使って予測を実行 |
| score(X,y[,sample_weight]) | 決定係数R2を出力 |
| set_params(**params) | パラメータを設定 |
単回帰分析について
説明変数が1つのもの
最小二乗法
公式の導出
データと回帰した直線の差(二乗誤差関数)が最小になるようにする
$$E_D=\sum_{i=0}^{n}e_i^2=\sum_{i=0}^{n}(Y_i-aX_i-b)^2$$
$$E_D:二乗誤差関数, e:残差, Y=aX+bに対して回帰を実行$$
最小値を求めるなら微分!
残差の二乗式を偏微分を使って微分して、0になるところが最小
$$\frac{∂\sum_{i=0}^{n}}{∂a}=-2\sum_{i=0}^{n}(Y_i-aX_i-b)X_i=0 -①$$
$$\frac{∂\sum_{i=0}^{n}}{∂b}=-2\sum_{i=0}^{n}(Y_i-aX_i-b)=0 -②$$
の連立方程式を解く。ここで、
$$E(X)=\frac{1}{n}\sum_{i=0}^{n}X_i=\bar{X}とすると$$
$$②より、\frac{∂\sum_{i=0}^{n}}{∂b}=0=\sum_{i=0}^{n}Y_i-a\sum_{i=0}^{n}X_i-nb$$
$$∴ b=\bar{Y}-a\bar{X} -③$$
これを①に代入して
$$\frac{∂\sum_{i=0}^{n}}{∂a}=0=\sum_{i=0}^{n}X_iY_i-n\bar{X}\bar{Y}-a\Bigl(\sum_{i=0}^{n}X_i^2-n\bar{X}^2\Bigr)$$
$$ここで、\sum_{i=0}^{n}X_i\bar{Y}=\sum_{i=0}^{n}\bar{X}Y_i=\sum_{i=0}^{n}\bar{X}\bar{Y}$$
$$Cov[X,Y]=\frac{1}{n}\sum_{i=0}^{n}(X_i-\bar{X})(Y_i-\bar{Y})$$ $$Var[X]=\frac{1}{n}\sum_{i=0}^{n}(X_i-\bar{X})^2$$
であることより
$$a=\frac{\sum_{i=0}^{n}(X_iY_i-Xi\bar{Y}-\bar{X}Y_i+\bar{X}\bar{Y})}{\sum_{i=0}^{n}(X_i^2-2X_i\bar{X}+\bar{X}^2)}$$
$$=\frac{\sum_{i=0}^{n}(X_i-\bar{X})(Y_i-\bar{Y})}{\sum_{i=0}^{n}(X_i-\bar{X})^2}$$
$$=\frac{Cov[X,Y]}{Var[X]}$$
③に代入して
$$b=\bar{Y}-\frac{Cov[X,Y]}{Var[X]}\bar{X}$$
$$Y=aX+bに代入して最小二乗法公式が得られる$$
$$Y-\bar{Y}=\frac{Cov[X,Y]}{Var[X]}(X-\bar{X)}$$
決定係数R2
*R2*は以下のように定義される。
$$R^2=1-\frac{\sum_{i=0}e_i^2}{\sum_{i=0}(Y_i-\bar{Y})^2}=1-\frac{RSS}{TSS}$$
すなわち、残差の二乗和を標本値の平均からの差の二乗和で割ったものを1から引いた値であり、1に近いほど相対的な残差が少ないことを示している。
必要なライブラリとデータセットの読み込み
import itertools
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import linear_model
from sklearn import datasets
sns.set()
# download datasets
wine_data = datasets.load_wine()
wine = pd.DataFrame(wine_data.data, columns=wine_data.feature_names)
ライブラリを使って単回帰分析を実行する
clf = linear_model.LinearRegression()
X=wine.loc[:,['total_phenols']].values
Y=wine['flavanoids'].values
clf.fit(X,Y)
print("回帰係数=", clf.coef_)
print("切片:",clf.intercept_)
print("R^2=",clf.score(X, Y))
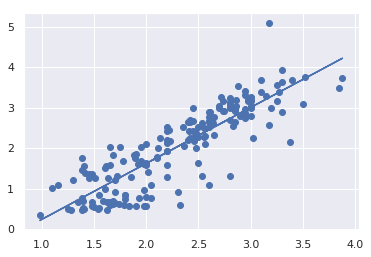
plt.scatter(X, Y)
# 回帰直線
plt.plot(X, clf.predict(X))
実行結果
回帰係数= [1.37984391]
切片: -1.137627158404063
R^2= 0.7474700456967156
最小二乗法の単回帰分析をPythonで実装する
class Least_squares_method(object):
'''
Xを説明変数、Yを目的変数とした最小二乗法を実行し、決定係数と編回帰変数を返す
また、決定係数と編回帰係数を記載したグラフを書く
'''
def __init__(self, X, Y):
self.X=X
self.Y=Y
if len(X)!=len(Y):
raise ValueError('The dimensions of X and Y must be equal')
self.E_X=X.mean()
self.E_Y=Y.mean()
self.var_X=X.var()
self.cov=np.cov(X,Y)[0,1]
def execute_regression(self):
self.a=self.cov/self.var_X
self.b=self.E_Y-self.a*self.E_X
return self.a, self.b
def get_R(self):
self.RSS=0
self.TSS=0
for i in range(len(self.X)):
self.RSS+=(self.Y[i]-self.a*self.X[i]-self.b)**2
self.TSS+=(self.Y[i]-self.E_Y)**2
self.R2=1-self.RSS/self.TSS
return self.R2
def plot_result(self):
a, b=self.execute_regression()
y=a*self.X+b
R2=self.get_R()
title="R^2="+str(R2)
fig=plt.figure()
ax=fig.add_subplot(111)
ax.scatter(self.X, self.Y)
ax.plot(self.X, y)
ax.set_title(title)
model1=Least_squares_method(X.T[0],Y)
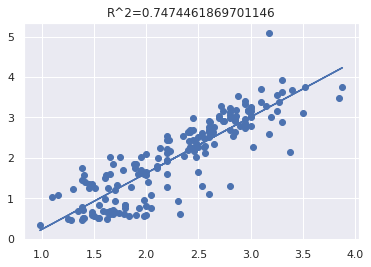
model1.plot_result()
実行結果
結論
実装できた。ポリフェノール量と色素量で回帰したけどまあ当然相関係数高いよねという結論です。数式もう少し綺麗にかけるように工夫したい。次回は重回帰分析をかけるといいなあ。
2020/5/7 更新
as_matrix() -> values