1. はじめに
昨今の大規模言語モデル(LLM; Large Language Model)の開発・発展のスピードは目覚ましいものがあり、研究やビジネスの場に留まらず、ChatGPTをはじめとしてふだんの生活の中でLLMを活用されている方も増えてきているのではないでしょうか。
LLMの研究開発においては、様々な観点でその性能を評価し、より性能の高いLLMの探求が進められています。ただ、評価観点の中でも、数学的推論能力(例:与えられた計算問題を正しく解くことができるか?)については、性能評価はされてきているものの、LLMが本当に数学的な知識を理解し、それを活用して計算問題を解いているのかについては議論が継続しています。この記事では、2024年2月に公開された論文 GSM-Plus: A Comprehensive Benchmark for Evaluating the Robustness of LLMs as Mathematical Problem Solvers をもとに、LLMの数学的推論能力の評価について簡単にご紹介します。(LLMの基礎的な概要についてはこちらをご参照ください。)
なお、この記事は2024年2月時点の情報をもとにしていることにご留意ください。
なぜ数学的推論能力の評価に着目したか?
LLMの活用方法はまだまだ発展途上ですが、たとえばLLMを使って事務処理を効率的にこなしたいというケースについて考えてみます。LLMで処理したいタスクに金額などの計算が含まれるとき、この計算結果が誤っていると、結局人間の手で再計算・検算をしなくてはならず、あまり手間の削減にはならないでしょう。LLMが(ほぼ)間違いなく計算をしてくれることがわかれば、計算を含む事務処理をLLMで自動化できそうです。したがって、現状のLLMの数学的推論能力を評価することは、LLMを活用できるシーンを把握することにもつながり、実用上のメリットがあります。
2. 論文「GSM-Plus:~」の要点
この論文は、LLMの数学的推論能力の頑健性を評価するためのベンチマーク「GSM-Plus」を紹介しています。GSM-Plusは、既存のGSM8Kデータセット(小学校レベルの数学問題)をもとに、様々な摂動(問題の変形)を加えた10,552個の問題のバリエーションから構成されます。25個のLLMを対象とした実験によると、LLMは基本的な数学問題には高精度で解答できるものの、問題の表現が少し変わるだけで精度が著しく低下します。これにより、LLMの数学的理解の限界を明らかにしています。
既存研究において、LLMは数学的推論能力を評価する様々なベンチマークにおいて高い性能を達成することが示されています。しかし、LLMは本当に数学的知識を理解し適用しているのか、それとも単に表面的な数字のパターンを使っているだけなのか、議論が続いています。数学的推論において本質的かつ頻繁に起こる問題点のひとつは、数学の問題が少し変更されたときに、LLMが誤った解答をすることです。このことが、LLMの数学的推論能力の頑健性を評価する動機となっています。
3. GSM-Plus
3-1. 数学的推論能力を評価するためのベンチマーク
数学的推論能力を評価するためのベンチマークとしては、GSM8K(小学校数学)、MATH(高校数学)、Theoremqa(大学数学)など、様々なものが使用されています。しかし、図1に示す通り、既存のデータセットは限られた種類の摂動しかカバーしていません。そこで、論文 GSM-Plus: A Comprehensive Benchmark for Evaluating the Robustness of LLMs as Mathematical Problem Solvers では、数学的推論能力の頑健性を評価するためのデータセットとして、GSM-Plusを提案しています。
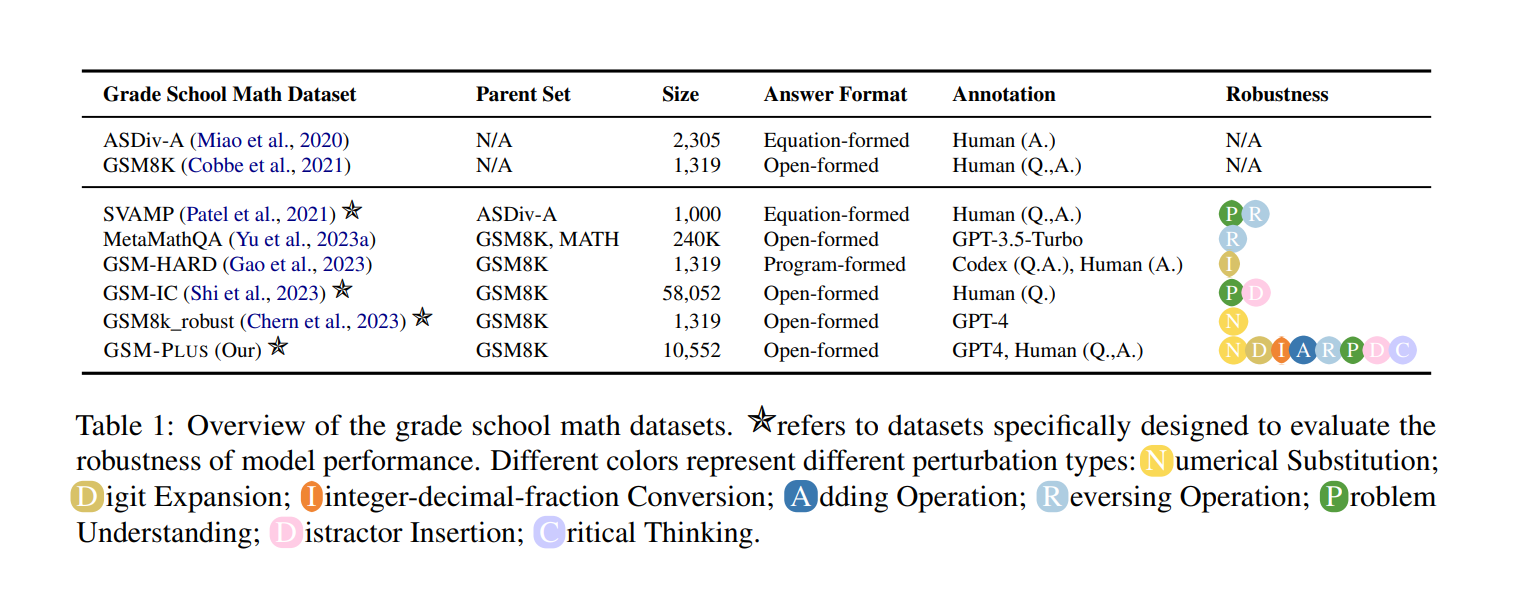
図1:小学校数学のデータセットの概要:データセット名に付いている星印は特に数学的推論能力の頑健性を評価するために設計されたデータセットであること、Robustnessの列は考慮している摂動の種類を示す(Qintong Li et al., 2024 Table 1を引用)
3-2. GSM-Plusの設計
GSM-Plusは、最も一般的に使用されているGSM8Kデータセットをもとに構築された、LLMの数学的推論能力の頑健性を包括的に評価するためのデータセットです。GSM-Plusでは、数学的推論能力の頑健性を検証するための5つの観点をもとにした8種類の摂動を考慮しています。
3-2-1. 摂動
数学の問題文を変形することを摂動と呼びます。GSM-Plusで考慮している摂動を以下に示します。
-
Numeric variation:問題文中の数値を変更し、LLMが過剰適合していないかを検証する
- Numerical Substitution:数値を同じ桁数の別の数値に置き換える(例:16→20)
- Digit Expansion:数値の桁数を増やす(例:16→1,600)
- Integer-decimal-fraction Conversion:数値の型を変更する(例:2→2.5)
-
Arithmetic variation:数学の演算子の適用における柔軟性を検証する
- Adding Operation:問題文中に、四則演算が含まれる文を追加する
- Reversing Operation:問題文を変形し、数値を回答する対象を変更する
- Problem understanding:問題文を言い換え、LLMの問題理解に対する影響を検証する
- Distractor insertion:問題文に関連するが、回答には役に立たない文を追加する
- Critical thinking:問題文から回答に必須の記述を取り除き、疑問を呈するかを検証する
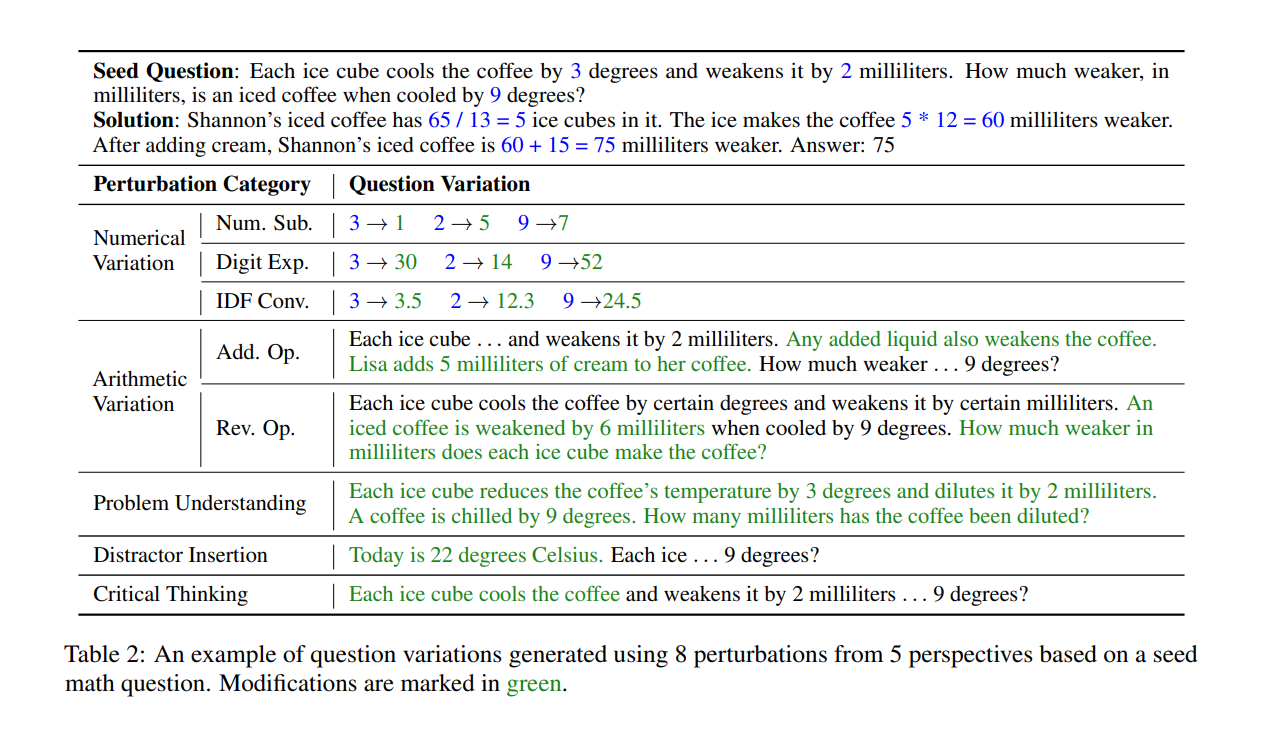
図2:もととなる数学の問題文(seed question)および、5つの観点にもとづく8種類の摂動の例(Qintong Li et al., 2024 Table 2を引用)
3-2-2. GSM-Plusの構築
GSM-Plusは、まず問題文の変形およびそれに対する回答をGPT-4で生成し、人間のアノテーターが確認・修正をすることで構築されています。複数人のアノテーターがクロスチェックすることで、データの品質を担保しています。
このようにして、GSM8Kの1,319個の問題文をもとに、各問題について8種類の摂動を加えた10,552個のバリエーションを作成します。
4. 数学的推論能力の頑健性の評価
4.1 評価指標
摂動の影響を評価するため、PDRとASPの2つの評価指標を使用します。
PDR(Performance Drop Rate)
PDRは、摂動を加える前(GSM8K)と比較して、摂動を加えることでどれだけ問題の正解率が減少したかを示す指標です。
PDR = 1 - \frac{\sum_{(x,y)\in D_a} \mathbb{I}[LM(x), y]/|D_a|}{\sum_{(x,y)\in D} \mathbb{I}[LM(x), y]/|D|}
$D_a, D$はそれぞれGSM-Plus、GSM8Kのデータセットを表します。
ASP(Accurately Solved Pairs)
ASPは、摂動を加える前の問題 $x$ と摂動を加えた問題 $x'$ のペアがともに正解した割合を示す指標です。
ASP = \frac{\sum_{(x,y;x',y')} \mathbb{I}[LM(x), y] \cdot \mathbb{I}[LM(x'), y']}{N \cdot |D|}
$N$ は各問題文に加えられる摂動の種類数を表し、問題文および回答 $(x, y)$ と摂動を加えた問題文および回答のペアを $(x,y;x',y')$ で表しています。
4-2. 評価結果
論文中では、GPT-4, GPT-3.5-Turbo, LLaMA-2などのLLM、および数学的推論のためのデータセットで教師ありファインチューニング(SFT; Supervised Fine-Tuning)を施したMetaMath, Abel, ToRAを含む25個のモデルを対象に、数学的推論能力の頑健性を評価しています。
4-2-1. 評価結果の概要
評価の結果、いずれのモデルでも性能の低下が見られました(図3)。GPT-4が最も頑健性が高い(PDR 8.23%)ものの、より頑健性高く数学的推論を行うには、自然言語によるガイドやタスクに特化したファインチューニングが必要であることが示唆されます。
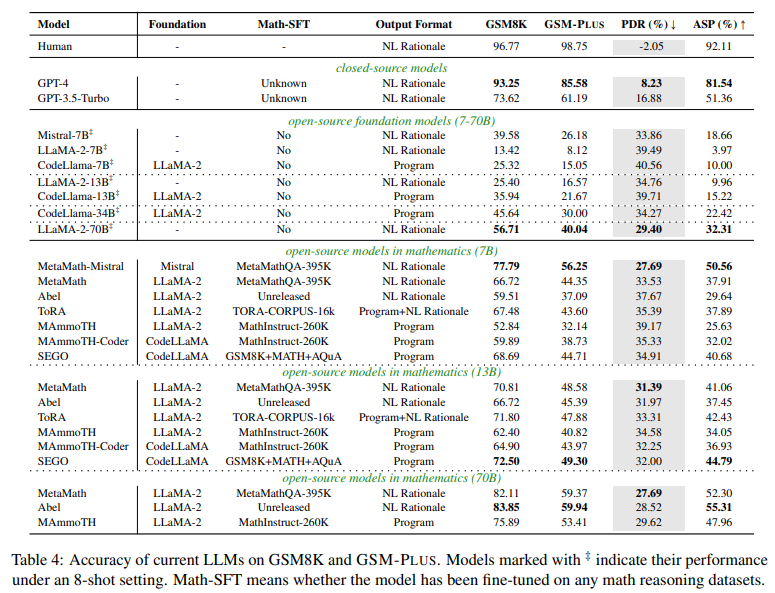
図3:LLMの数学的推論能力の評価結果(Qintong Li et al., 2024 Table 4を引用)
4-2-2. 摂動の影響
論文中では、8種類のそれぞれの摂動に対する性能も評価されています(図4)。いずれのモデルでも、critical thinking(紫)、adding/reversing operation(青)、distractor insertion(桃)、integer-decimal-fraction conversion(橙)に対する頑健性が低く、numerical substitution, digit expansion, problem understandingに対する頑健性が高いことが示されています。GPT-4, GPT-3.5-Turboは比較的良好な性能を示しているものの、人間(図中のHuman)に比べると、摂動による性能の低下が著しいといえます。
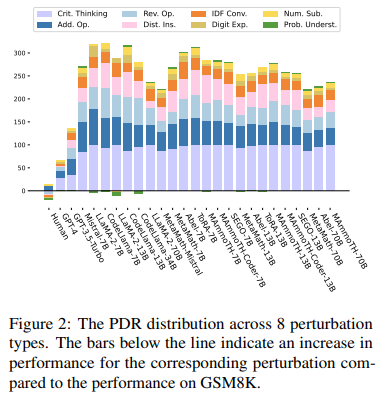
図4:8種類の摂動に対するPDR(Qintong Li et al., 2024 Figure 2を引用)
4-2-3. 数学的推論能力の転移性(transferability)
次に、ASPの評価結果を見てみます(図5)。数学的推論のためにSFTを施したモデルの中でもAbel-70B のASPが高く(55.31%)、GPT-3.5-TurboのASP(51.36%)を上回っています。しかし、いずれのモデルでも、摂動を加える前の問題には正しく回答できるものの、摂動を加えると不正解になってしまう問題(図5の赤)が一定数あり、数学的推論能力の転移性が限られものであることを示唆しています。また、もとの問題に正解できる割合(図5の赤+紫)がモデルによってまちまちである一方で、いずれのモデルも転移性は同じような水準に留まっている(図5の赤)ことから、既存のデータセットは、LLMの数学的推論能力(の頑健性)を正しく評価できていないことが示唆されます。
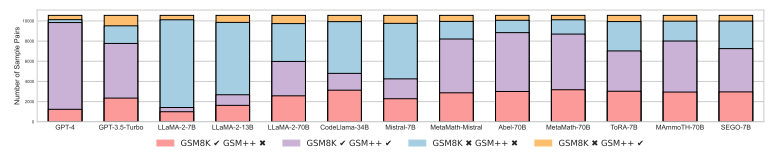
図5:GSM8KとGSM-Plusの正誤別問題ペア数:GSM8Kで正解しGSM-Plusで不正解の問題ペアが赤、GSM8K/GSM-Plusともに正解の問題ペアが紫、GSM8K/GSM-Plusともに不正解の問題ペアが青、GSM8Kで不正解しGSM-Plusで正解した問題ペアを黄で示す(Qintong Li et al., 2024 Figure 3を引用)
4-2-4. プロンプト技術の影響
既存研究においても、LLMに論理展開を明示的に与えるプロンプト技術を活用することで、LLMの数学的推論能力が向上することが実証されています。この論文では、以下の4つのプロンプト技術がLLMの性能にどう影響するかを評価しています。
- CoT(Chain-of-Thought)prompting
- PoT(Program-of-Thought)prompting
- LtM(Least-to-Most)prompting
- 複雑な問題を一連の副問題に分解することで、課題解決プロセスを簡潔にする手法
- Complexity-based CoT
- より多くのステップを持つ例を文脈内のデモンストレーションとして使用し、LLMの推論能力を向上させる手法
GPT-4, GPT-3.5-Turbo, LLaMA-2-70B, MAmmoTH-70B を対象とした性能評価では、前者の3つのモデルにおいて、Complexity-based prompting が最も良い性能を示しています(図6)。
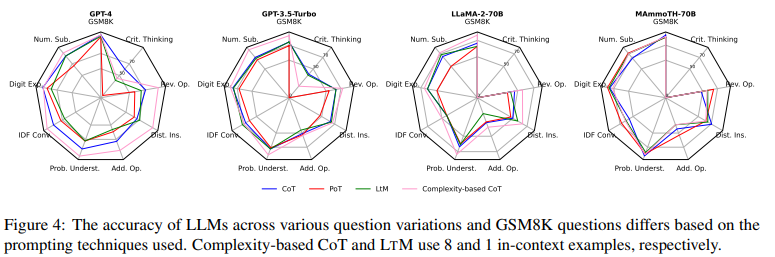
図6:プロンプト技術ごとの8種類の摂動に対する正解率(Qintong Li et al., 2024 Figure 4を引用)
また、論文中ではCompositional Promptingというプロンプト技術(図7)の性能評価もなされていますが、LLMの性能(頑健性)へのインパクトは限定的であると結論付けられています。
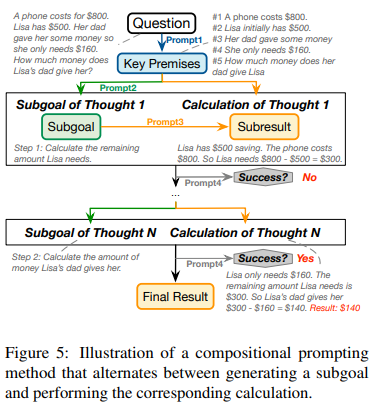
図7:Compositional Promptingの図解(Qintong Li et al., 2024 Figure 5を引用)
5. まとめ
この記事では、LLMの数学的推論能力の頑健性の評価に関する論文を紹介しました。
紹介した論文では、ほとんどのLLM、特にオープンソースのモデルの数学的推論能力が、人間に大きく及ばないことが示されていました。この記事の執筆時点では、数学を含むタスクをLLMで完全自動化するにはさらなる技術発展が必要なようです。最後に、LLMの数学的推論能力に関する今後の研究の方向性として、論文中では以下の2つが挙げられています。
- 様々な数学関連のスキルにおけるモデルの系統的な評価
- 数学的推論を一貫して柔軟に実行しつつ、問題文のわずかな変化にも対応できるモデルの開発
この記事が、LLMを開発・活用する方のご参考になれば幸いです。