1. はじめに
深層学習ベースの有名な生成モデルとしては、GANやVAEなどがよく知られています。近年、これらとは異なるアプローチをとる生成モデルとして、拡散モデルに関する研究が盛んになっています。特に文献[6]では定量的評価・定性的評価の両面で、拡散モデルによる画像生成品質がBigGANを超えたと報告されました。画像生成以外でも、音声合成(文献[13], [20])やテキスト処理(文献[12], [21])、ロボット制御(文献[20])などの種々のタスクへの応用事例が報告されており、ますます注目度の高い技術になっています。
本記事では、拡散モデルの代表であるdenoising diffusion probabilistic model(DDPM)による画像生成の理論的側面と、研究事例としてImagen [18]を紹介します。
2. 拡散モデルの基礎
2-1. 拡散過程・逆拡散過程の導入
拡散モデルのベースとなるのは、図1の左向きの拡散過程と、右向きの逆拡散過程(生成過程)です。拡散過程は画像 $x_0$に徐々にガウシアンノイズを加えていき、最終的に純粋なガウシアンノイズ $x_T$を得る過程です。これは単純にノイズを加えていくだけですので、簡単に追跡することが可能です。一方、逆拡散過程は純粋なガウシアンノイズ $x_T$が与えられたときにここから徐々にノイズを除去していき、最終的に鮮明な画像 $x_0$を得る過程です。こちらは拡散過程と異なり追跡が困難なことが容易に想像できると思いますが、もしこの過程に沿って $x_{(T-1)},x_{(T-2)},⋯,x_0$を得ることができれば、純粋なノイズから鮮明な画像を得ることができます。この逆拡散過程を利用して画像を生成するのが拡散モデルの基本的なアイデアです。
DDPMでは拡散過程・逆拡散過程がマルコフ過程(遷移確率が現在の状態のみに依存し、それまでの履歴に依らない過程)であり、それぞれの遷移確率が $q(x_t│x_{t-1} ),q(x_{t-1}│x_t )$によって表現できることを仮定します。もし逆拡散過程の遷移確率 $q(x_{t-1}│x_t )$を捉えることができれば、純粋なノイズ $x_T$から $q(x_0│x_T )$を求めることが可能です。これは純粋なノイズ $x_T$から鮮明な画像 $x_0$を生成できることを意味します。したがって、$q(x_{t-1}│x_t )$の具体的な表式を見つけたいわけですが、これは非常に難しい問題です。そこで、逆拡散過程の遷移確率を、学習によって定まるパラメータ $θ$を持つニューラルネットワークの出力 $p_θ (x_{t-1} |x_t)$によって近似します。次節以降では、追跡が容易な拡散過程の遷移確率 $q(x_t│x_{t-1} )$を用いて、最適なパラメータ $θ$を求める手続きを導出します。
2-2. 拡散過程の定式化
上で述べたように、拡散モデルで重要となるのは逆拡散過程ですが、これを直接捉えるのは難しい問題です。一方で、拡散過程は画像にノイズを加えていくだけの過程ですので、比較的簡単に追跡することができます。そこで、まずは拡散過程について具体的な定式化をおこないます。ここでの結果は、逆拡散過程を追跡する際に利用されます。
拡散過程は、元の画像を $x_0$として、これに徐々にガウシアンノイズを付加して $x_1,x_2,⋯,x_T$を生成していく過程です。ここで、$x_T$は純粋なガウシアンノイズです。この過程は漸化式の形で
x_t=\sqrt{1-β_t} x_{t-1} + \sqrt{β_t} \epsilon_t \tag{1} \\
t=1,2,⋯,T
と書くことができます。ここで $\epsilon_t \sim N(0,I)$は標準正規分布に従うノイズ($I$は $x_t$と同じ次元の単位行列)、$\beta_t \in (0,1)$は時刻 $t$で加えるノイズの大きさを表すパラメータで、事前に決めておくパラメータです。(例えばHoら(文献[7])は線形にノイズの大きさを増やす方式を採用: $\beta_1=10^{-4},\beta_T=0.02$。)最終的なノイズ強度がステップ数 $T$に露わに依存しないようにするため(特に $T \rightarrow \infty$で発散しないようにするため)、信号を $\sqrt{1-β_t}$倍に減衰したあとにノイズを加える形をとっています。また、これは条件付確率の形で
q(x_t│x_{t-1} ) = N(x_t;\sqrt{1-\beta_t } x_{t-1},\beta_t I) \tag{2}
と書くこともできます。拡散過程の漸化式(1)を繰り返し利用すると、任意の時刻 $t$における $x_t$は $x_0$を減衰した信号に平均ゼロのガウシアンノイズ $\epsilon_1,\epsilon_2,⋯,\epsilon_t$の線形結合を加えて得られることが分かります。ここで、正規分布に従うノイズの和はまた正規分布に従うという性質($z_1 \sim N(\theta,\sigma_1^2 I),z_2 \sim N(\theta,\sigma_2^2 I$)に対して$z_1 + z_2 \sim N(\theta,(\sigma_1^2 + \sigma_2^2 )I)$)を利用すると、加えられる $\epsilon_1,\epsilon_2,⋯,\epsilon_t$の線形結合はただ一つのガウシアンノイズ $\epsilon \sim N(0,I)$で表現できることが分かります。結果的に、
x_t = \sqrt{\bar{\alpha}_t } x_{0} + \sqrt{1-\bar{α}_t } \epsilon \tag{3}
と単純な形で書くことができます。ここで$\alpha_{t} = 1-\beta_{t}$, $\bar{\alpha}_t = \prod _{s=1} ^{T} \alpha _{s}$です。これは条件付確率の形で書くと、次のようになります:
q(x_t│x_0 )=N(x_t;\sqrt{\bar{α}_{t}}x_0,\sqrt{1-\bar{\alpha}_t} I) \tag{4}
したがって、拡散過程における任意の時刻の信号 $x_t$は、逐次的な遷移を繰り返すことなく初期値 $x_0$から直接算出することができます。式(4)は逆拡散過程の確率分布を求める際に利用されます。
2-3. 条件付き逆拡散過程の定式化
生成モデルの主役である逆拡散過程の遷移確率 $q(x_{t-1}│x_t )$そのものを得ることは難しいですが、ノイズ付与前の画像 $x_0$で条件づけた場合の遷移確率 $q(x_{t-1} |x_t,x_0)$は、先ほど求めた式(4)を利用すれば具体的な表式を得ることが可能です。ここでは、$q(x_{t-1} |x_t,x_0)$の具体的な表式を求めます。ここで求めた結果は損失関数の導出に利用されます。
拡散過程の結果を利用するために、ベイズの定理を用いて逆拡散過程の遷移確率を
q(x_{t-1}│x_t,x_0 )=\frac{q(x_t│x_{t-1},x_0 )q(x_{t-1}│x_0 )}{q(x_t│x_0)}\\
= \frac{q(x_t│x_{t-1} )q(x_{t-1}│x_0 )}{q(x_t│x_0 )} \tag{5}
と書き直します。2番目の等号では、拡散過程におけるマルコフ性: $q(x_t│x_{t-1},x_0 )=q(x_t│x_{t-1} )$を利用しました。ここで、上式右辺に現れる3つの確率分布は全て拡散過程で現れるもので、これらの具体的な表式は全て前節で求めた式(2)と式(4)から分かります。規格化定数の部分を無視すると、それぞれ下記のとおりです。
q(x_t│x_{t-1},x_0 ) \propto \exp \Biggl[-\frac{1}{2} \frac{(x_t- \sqrt{α_t} x_{t-1})^2}{\beta _t} \Biggr]
q(x_{t-1}│x_0 ) \propto \exp \Biggl[-\frac{1}{2} \frac{ (x_{t-1}-\sqrt{\bar{\alpha} _{t-1} } x_0 )^2}{1- \bar{\alpha} _{t-1} } \Biggr]
q(x_t│x_0 ) \propto \exp \Biggl[-\frac{1}{2} \frac{(x_t-\sqrt{\bar{\alpha} _t } x_0 )^2}{1- \bar{\alpha} _t } \Biggr]
式(5)から $x_{t-1}$の条件付き分布を求めるのが目的なので $x_{t-1}$に着目すると、これらはexpの中身が全て二次以下の式になっています。したがって、これらを式(5)に代入すると、条件付き逆拡散過程の遷移確率も正規分布となることが分かります:
q(x_{t-1}│x_t,x_0 ) \propto \exp[-\frac{1}{2} \frac{(x_{t-1} - \tilde{\mu} _t (x_t,x_0 ))^2}{\tilde{β}_t} ] \tag{6}
ここで正規分布の平均値と分散はそれぞれ
\tilde{\mu} _t (x_t,x_0 ) = \frac{ \sqrt{\alpha_t} (1- \bar{\alpha} _{t-1} )}{1 - \bar{\alpha} _t } x_t + \frac{\sqrt{\bar{\alpha} _{t-1}}\beta _t}{1-\bar{\alpha} _t} x_0 \tag{7} \\
\tilde{\beta} _t = \frac{1-\bar{\alpha} _{t-1}}{1- \bar{\alpha} _t }\beta_t \tag{8}
です。つまり、$q(x_{t-1}│x_t,x_0 ) = N(x_{t-1};\tilde{\mu} _t(x_t,x_0 ),\tilde{\beta} _t I)$です。
これで条件付き逆拡散過程の具体的な表式が得られました。更に画像生成時に使われる式を導いておきます。式(3)を $x_0$について解いた式 $x_0 = \frac{1}{\sqrt{\bar{\alpha_t}}}(x_t - \sqrt{1 - \bar{\alpha_t}}\epsilon)$を式(7)に代入すると、
\tilde{\mu} _t = \frac{1}{\sqrt{\alpha}_t } \Biggl( x_t - \frac{\beta_t}{\sqrt{1- \bar{\alpha} _t} } ϵ \Biggr) \tag{9}
とできます。 $\sigma_t^2=\tilde{\beta_t}$とおくと、
x_{t-1} = \tilde{\mu} _t + \tilde{\beta} _t z_t = \frac{1}{\sqrt{\alpha}_t }\Biggl( x_t - \frac{\beta_t}{\sqrt{1- \bar{\alpha} _t} } ϵ_t \Biggr) +\sigma_t^2 z_t \tag{10} \\
z_t \sim N(0,I)
が得られます。拡散モデルを用いて画像を生成する際には、式(10)にしたがって画像のサンプリングが行われます。
2-4. 損失関数の導出
前節までで、逆拡散過程の遷移確率の最適な近似 $p_{\theta} (x_{t-1} |x_t)$を求めるための準備が完了しました。いよいよこの節では、拡散モデルの学習で利用される損失関数を導出します。損失関数を最小化するようにパラメータ $\theta$を決定し、逆拡散過程の遷移確率を求めることができます。
拡散モデルの主役である逆拡散過程を考えます。これは、純粋なノイズ $x_T$から徐々にノイズを除いていって、元の画像 $x_0$を復元する過程です。この過程は $T$が十分大きければ(拡散過程で一回に加えるノイズが十分小さければ)、拡散過程と同様に正規分布を仮定することができます。ニューラルネットワークのパラメータを $\theta$として、
p_{\theta} (x_{t-1}│x_t ) = N(x_{t-1};μ_{\theta} (x_t,t),\Sigma_{\theta} (x_t,t) )
とします。平均 $\mu_{\theta}$、分散 $\Sigma_{\theta}$を学習によって決定することになりますが、ここではHoら(文献[7])に倣って $\mu_{\theta} (x_t,t)$だけを学習するための損失関数を導出します。分散は事前定義した式 $\Sigma_{\theta} (x_t,t)=\sigma_t^2 I=β_t I$とします。($\Sigma_{\theta}$を学習するような研究は文献[11]などがあります。)漸化式の形で書けば、
x_{t-1} = \mu_{\theta} (x_t,t) + \sigma_t^2 z_t \tag{11}
z_t\sim N(0,I)
です。
上の生成過程で生成された画像 $x_0$が自然な画像となることを課すために、生成画像の対数尤度を最大化するように平均 $\mu_θ (x_t,t)$を決定することにします。最小化問題とするため、対数尤度のマイナス1倍が目的関数となります。VAEの損失関数を求めるときと同様、変分下限を最小化する問題に変形し、最終的にノイズの二乗誤差となることを確認します。画像 $x_0$が分布 $q(x_0)$に従って生成されるとき、下記のように変形できます:
\begin{align}
&-\mathbb{E}_{q(x_0 )} [\log{p_{\theta}(x_{0})}]\\
&= - \int dx_0 q(x_0)\log{p_{\theta}(x_{0})} \\
&= - \int dx_0 q(x_0)\log{\Biggl( \int p_{\theta}(x_{0:T})dx_{1:T} \Biggr)} \\
&= - \int dx_0 q(x_0)\log{\Biggl( \int q(x_{1:T}|x_0)\frac{p_\theta (x_{0:T})}{q(x_{1:T}|x_0)}dx_{1:T} \Biggr)} \quad q(x_{1:T}|x_0)を掛けて割った\\
&\leq - \int dx_0 q(x_0)\Biggl( \int q(x_{1:T}|x_0)\log{\frac{p_\theta (x_{0:T})}{q(x_{1:T}|x_0)}dx_{1:T} \Biggr)} \quad {\rm jensen}の不等式\\
&= \mathbb{E}_{q(x_{0:T})} \Biggl[ \log{\frac{q(x_{1:T}|x_0)}{p_\theta (x_{0:T})}} \Biggr] := L_{\rm VLB}
\end{align}
さらに、拡散過程・逆拡散過程のマルコフ性を利用して同時分布を分解していきます:
\begin{align}
L_{\rm VLB} &= \mathbb{E}_{q(x_{0:T})} \Biggl[ \log{\frac{q(x_{1:T}|x_0)}{p_\theta (x_{0:T})}} \Biggr] \\
&= \mathbb{E}_{q(x_{0:T})} \Biggl[ \log{\frac{\prod _{t=1}^{T}q(x_{t}|x_{t-1})}{p_\theta (x_{T})\prod _{t=1}^{T} p_{\theta}(x_{t-1}|x_{t})}} \Biggr]\\
&= \mathbb{E}_{q(x_{0:T})} \Biggl[-\log{p_{\theta}(x_{T})} + \sum _{t=2}^{T} \log{\frac{q(x_{t}|x_{t-1})}{p_{\theta}(x_{t-1}|x_{t})}} + \log{\frac{q(x_{1}|x_{0})}{p_{\theta}(x_{0}|x_{1})}} \Biggr] \\
&= \mathbb{E}_{q(x_{0:T})} \Biggl[-\log{p_{\theta}(x_{T})} +
\sum _{t=2}^{T} \log{
\frac{q(x_{t-1}|x_{t}, x_{0})}{p_{\theta}(x_{t-1}|x_{t})}
\frac{q(x_{t}|x_{0})}{q(x_{t-1}|x_{0})}}
+ \log{ \frac{q(x_{1}|x_{0})}{p _{\theta}(x_{0}|x_{1})} } \Bigr] \ 式(5)を利用\\
&= \mathbb{E}_{q(x_{0:T})} \Biggl[
\log{\frac{q(x_{T}|x_0)}{p_\theta (x_{T})}} +
\sum _{t=2}^{T} \log{
\frac{q(x_{t-1}|x_{t}, x_{0})}{p_{\theta}(x_{t-1}|x_{t})}
}
- \log{p_{\theta}(x_{0}|x_{1})}
\Biggr] \\
&= \mathbb{E}_{q} \Biggl[
D_{\rm KL}(q(x_{T}|x_0) \parallel p_{\theta}(x_T))
+ \sum _{t=2}^{T} D_{\rm KL}( q(x_{t-1}|x_{t}, x_{0}) \parallel p_{\theta}(x_{t-1}|x_{t})) \\
&\quad\quad\quad\ - \log p_{\theta}(x_{0}|x_{1}) \Biggr] \\
&= L_{T} + L_{T-1} + \cdots + L_{0}
\end{align}
ここで
L_T = \mathbb{E}_q [ D_{\rm KL} (q(x_T│x_0 )\parallel p_{\theta} (x_T )] \\
L_t = \mathbb{E}_q [ D_{\rm KL} (q(x_{t-1}│x_t,x_0 )\parallel p_{\theta} (x_{t-1}│x_t )) ]\ \text{for}\
t=1,2,⋯,T-1 \\
L_0 = -\mathbb{E}_q [\log p_{\theta} (x_0│x_1 )]
です。このうち $x_T$が純粋なガウシアンノイズであるため $L_T$は $\theta$に依存しません。また $L_0$も計算可能です(文献[7])。
残った $L_t (t=1,2,⋯,T-1)$を考えると、これらは正規分布同士のKLダイバージェンスなので、解析的に計算できます。つまり、
L_t = \mathbb{E}_q \Biggl[ \frac{1}{2\sigma_t^2 } \parallel \tilde{\mu}_t (x_t,x_0 )- \mu_{\theta} (x_t,t) \parallel^2 \Biggr] + C \tag{12}
です。これを最小化することは、条件付き逆拡散過程の遷移確率の平均値 $\tilde{\mu_t} (x_t,x_0 )$を、モデルの出力 $\mu_{\theta} (x_t,t)$で近似することを意味します。ところで、$\tilde{\mu_t} (x_t,x_0)$とノイズ $\epsilon$の関係は式(9)で与えられます。これに対応して、$\mu_{\theta} (x_t,t)$に対応するノイズ $\epsilon_{\theta}$を
\mu_{\theta} (x_ t,t) = \frac{1}{\sqrt{\alpha_t }} \Biggl( x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t }} \epsilon_{\theta} \Biggr)\tag{13}
で定義し、式(9),(13)を用いて式(12)を書き直すと、
\begin{align}
L_t &= \mathbb{E}_q \Biggl[ \frac{\beta_t^2}{2\alpha_t (1- \bar{\alpha}_t ) \sigma_t ^2 } \parallel \epsilon - \epsilon_{\theta} (x_t,t) \parallel^2 \Bigg] \\
&= \mathbb{E}_q \Biggl[\frac{\beta_t^2}{2\alpha_t(1- \bar{\alpha}_t) \sigma_t^2 } \parallel
\epsilon - \epsilon_{\theta} (\sqrt{\bar{\alpha}_t } x_0 + \sqrt{1-\bar{\alpha}_t } \epsilon_t,t) \parallel^2 \Biggr]
\end{align}
が得られます。Hoら(文献[7])はこれを更に簡略化して、
L_t^{\rm simple} = \mathbb{E}_q [\parallel \epsilon - \epsilon_{\theta} (\sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t } \epsilon_t,t)\parallel^2 ]\tag{14}
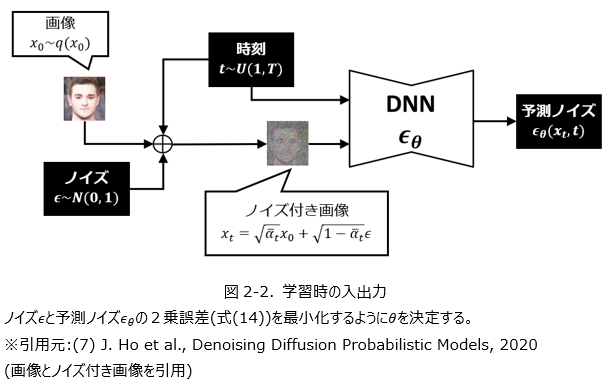
を利用しました。係数を簡略化する理論的根拠は特にないようですが、経験的には簡略化した式(14)で問題なく、後続の研究でもこちらが主に利用されます。以上でDDPMで利用される損失関数の導出ができました。これを用いた最適化の様子は図2-1,2-2で示しています。訓練用サンプル $x_0$と時刻 $t$を変えながら、加えられているノイズを推定するようにモデルが訓練されます。
モデルを学習した後、実際に画像を生成する手続きを示したのが図3です。ここではランダムなガウシアンノイズ $x_T$から出発して、ニューラルネットワークによって推定されたノイズ $\epsilon_{\theta} (x_t,t)$を徐々に除いていき、最終的に鮮明な画像 $x_0$が得られることになります。
2-5. DDIM・推論時間の削減
ここまで、DDPMの推論の過程は式(10)で与えられ、$z_t \sim N(0,I)$が乱数であるため確率的な過程となることを見ました。また、DDPMの損失関数は、式(14)になることを見ました。式(14)の導出においては、式(4) $q(x_t│x_0 ) = N(x_t;\sqrt{\bar{\alpha_t}} x_0,\sqrt{1- \bar{\alpha_t}} I)$が成立することが本質的で、$q(x_{1:T} |x_0)$の形には依存しません。詳細は省略しますが、$\sigma_t$に依存する逆拡散過程:
q_{\sigma} (x_{t-1}│x_t,x_0 )=N \Biggl( x_{t-1};\sqrt{\bar{\alpha}_{t-1}} x_0 +
\sqrt{1-\bar{\alpha}_{t-1} - \sigma_t^2 } \frac{x_t-\sqrt{\bar{\alpha}_t} x_0}
{\sqrt{1-\bar{\alpha}_t} } , \sigma_t^2 I \Biggr)\tag{15}
を考えると、ここから式(4)と同一の形で拡散過程を表すことができます(詳細は文献[10]を参照)。したがって、損失関数も式(14)の形になります。特に、式(8)の $\sigma_t^2 = \tilde{\beta_t}$と定めると、その生成過程はDDPMに帰着します。また、$\sigma_t^2=0$のときには乱数に依存する部分がなくなり、逆拡散過程の推論が確定的になります。この確定的な推論を利用した拡散モデルはDDIM (denoising diffusion implicit model, 文献[10])と呼ばれます。DDIMでは生成が確定的になったことによって、潜在空間上での特徴量を連続的に変化させることにより、画像を徐々に変化させることが可能になります(図5)。
拡散モデルは、GANなどの他の生成モデルと比べると、推論に非常に時間がかかることが課題です。これは、拡散過程ではランダムなノイズから出発して、$x_T,x_{T-1},\cdots,x_0$と徐々にノイズを除去する手続きを経る必要があるためです。
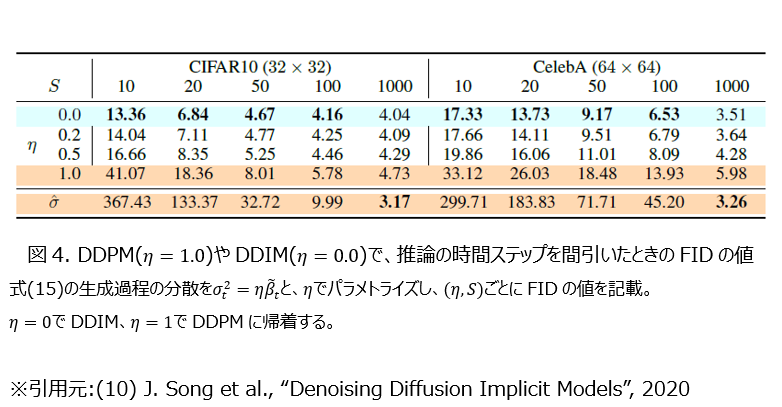
この課題の簡単な解決方法として、生成時の時間間隔を大きくし、$⌈T⁄S⌉$ごとに生成する方法が提案されています(文献[11])。例えば、$S=10,T=1000$のときには $x_{1000},x_{900},⋯,x_{100},x_0$と生成されることになり、10回の推論で最終的な出力が得られることになります。図4はDDIMやDDPMでこの推論方法を採用したときのFID(小さいほど生成される画像の品質が高いことを示す指標)の値を示したものです。DDPM($\eta=1.0$)は小さい $S$ではFIDの値が大きく、生成される画像の品質が大きく落ちることを意味しています。一方で、DDIM($\eta=0.0$)では小さい $S$でもFIDの値はそれほど大きくなることがないことが分かります。
2-6. 条件付けした画像の生成
特定のクラスの画像を選択的に生成したいことがあります。この節では、拡散モデルでこれを実現する方法として、classifier guidance(文献[6])とclassifier-free guidance(文献[22])を紹介します。
(a) Classifier guidance
Classifier guidanceでは、拡散モデルの他にクラス分類器(classifier) $p_{\phi}(c│x_t )$を用意しておく必要があります。画像 $x_t$を入力して、クラス $c$の確率を出力するようなモデルです。拡散過程でノイズが付与された画像に対応できる必要があるため、一般的な分類器では不十分で、新たに用意する必要があります。拡散モデルはクラスを指定しない場合と同様、式(14)の損失関数に従って学習しておきます。クラス指定なしの場合、拡散モデルの出力としてノイズの出力値 $\epsilon_{\theta} (x_t)$が得られますが、これを次のように補正します:
\tilde{\epsilon}_{\theta} (x_t,c) = \epsilon_{\theta}(x_t )-w\sigma_t \bigtriangledown_{x_t} \log{p_{\phi} (c│x_t )}
ここで、$w$は補正項の大きさをコントロールするためのパラメータで、事前に定義しておくものです。$w$が大きいほど生成される画像の多様性は小さくなりますが、品質は高くなります。生成過程で $x_{t-1}$を得る際には、$\epsilon_{\theta}$の代わりに $\tilde{\epsilon_{\theta}}$を利用してデノイズをおこないます。補正項 $\sigma_t \triangledown_{x_t } \log{p_{\phi} (c|x_t)}$によって分類器によるクラス $c$への予測確率が高い画像を生成するようになり、目的の画像が得られることになります。
(b) Classifier-free guidance
Classifier guidanceでは拡散モデルとは別にクラス分類器を用意する必要があり、モデル構築のパイプラインが複雑になってしまいます。そこで、拡散モデルだけで完結する方法として、文献[22]ではClassifier-free guidanceと呼ばれる方法が提案されました。クラス分類モデルを別個で作成する代わりに、拡散モデルに対してクラスラベル $c$を入力できるように変更します: $\epsilon_{\theta} (x_t,c)$。特にクラスを指定しない場合には $c=0$を入力するものと考えます。学習のときに使う損失関数はクラスを指定しない場合の式(14)を利用しますが、ランダムにクラスを指定しない場合($c=0$)とクラスを指定する場合($c\neq 0$)を混成して学習を行います。結果得られるクラス指定拡散モデル $\epsilon_{\theta} (x_t,c)$は、クラス $c$の画像を生成するように学習したことになるので、これを使ってデノイズすればクラス $c$の画像が生成されることが期待されます。生成過程にしたがって画像を生成する際には、クラス指定しない拡散モデル $\epsilon_{\theta} (x_t ) := \epsilon_{\theta} (x_t,c=0) $と線形結合した出力を利用します:
\tilde{\epsilon}_{\theta} (x_t,c) = \epsilon_{\theta}(x_t )+w(\epsilon_{\theta} (x_t,c) - \epsilon_{\theta} (x_t ))
ここで、$w$は事前定義するパラメータで、classifier-guidanceと同様に $w$が大きいほど生成される画像の多様性は小さくなり、個別の画像の品質は向上します。特に大きい $w$を設定した場合には、生成過程の各タイムステップで生成される画像のピクセル値が、想定される範囲(例えば[-1,1])を超えてしまうことが報告されています。これが起きると、最終的に生成される画像が自然なものではなくなってしまったり、時には発散してしまうことが起こり得ます。この問題に対処するため、生成過程の各画像でクリッピング処理をおこなうことが有効です(文献[18])。
3. 最近の拡散モデルの研究事例: Imagen
前節までで拡散モデルの基本について説明しました。ここでは、最近の研究事例として、2022年にGoogle Researchから発表されたImagen [18]を紹介します。
Imagenによる画像の生成結果の例を図6に示します。この例では、状況を表す適当な文章を入力することで、それに対応するような画像が生成されています。例えば、図6の中央の例では、“A cute corgi lives in a house made out of sushi.”という文章が入力されて、実際に寿司で作られた家の中から犬が顔を出した画像が生成されていることが確認できます。テキストから対応する画像を生成するような研究は盛んに行われていて、拡散モデルをベースにしたものも、Imagenの他にGLIDE [16]やDALL-E2 [15]などが知られています。ImagenはこれらのモデルにFIDなどの客観的な指標と、人による主観的な評価の両面で優れた結果を示したと主張しています。ここでは、簡単にImagenの動作原理について説明します。
図7に示すように、Imagenはテキストエンコーダ(Frozen Text Encoder)、テキストから画像を生成する拡散モデル(Text-to-Image Diffusion Model)、および2つの超解像拡散モデル(Super-Resolution Diffusion Model)の、計4つのニューラルネットワークから構成されます。テキストエンコーダは、自然言語で記述されたテキストを、その意味情報を含むような埋め込みベクトルに変換するようなニューラルネットワークです。テキストは抽象的な埋め込みベクトルに変換された後、後続の拡散モデルを通して画像に変換されます。ただし、この時点で生成されるのは64x64の低解像度のものになっています。これに対して超解像拡散モデルを適用し、64x64→256x256→1024x1024と、最終的には高解像度の画像が得られることになります。3つの拡散モデルでは、上述したclassifier-free guidanceを利用することで、テキスト情報に合致した画像の生成を実現しています。テキストエンコーダはテキストのみで学習したものをそのまま利用しており、本タスクのためのチューニングは行われていません。拡散モデルは画像-テキスト8.6億対から成る大量のデータセットを利用して学習しています。論文中ではより詳細な分析(テキストエンコーダや拡散モデルのサイズの探索、DALL-E2などの先行研究との比較など)が行われています。詳しくは論文を参照してください。
4. まとめ
本記事では、近年研究が盛んである拡散モデルの基本事項の説明と、最近の研究事例の紹介を行いました。研究事例としては、テキスト-画像の変換の例を紹介しました。この分野は非常に短いスパンで研究が報告されており、目まぐるしく発展していることが分かります。今回は画像生成に焦点を当てて紹介しましたが、音声合成や自然言語への応用も報告されています。今後もこの分野の発展に注目です。
5. 参考文献
[1] O. Avrahami et al., “Blended Diffusion for Text-driven Editing of Natural Images”, CVPR2022
[2] G. Kim et al., “DiffusionCLIP: Text-Guided Diffusion Models for Robust Image Manipulation”, CVPR2022
[3] R. Gal et al., “StyleGAN-NADA: CLIP-Guided Domain Adaptation of Image Generators”, 2021
[4] O. Patashnik et al.,, “StyleCLIP: Text-Driven Manipulation of StyleGAN Imagery”, 2021
[5] K, Crawson et al., “VQGAN-CLIP: Open Domain Image Generation and Editing with Natural Language Guidance”, 2021
[6] P. Dhariwal et al., “Diffusion models beat gans on image synthesis”, NeurIPS2021
[7] J. Ho et al., “Denoising Diffusion Probabilistic Models”, 2020
[8] C. Saharia et al., “Image Super-Resolution via Iterative Refinement”, 2021
[9] J. Sohl-Dickstein et al., “Deep Unsupervised Learning using Nonequilibrium Thermodynamics”, ICML2015
[10] J. Song et al., “Denoising Diffusion Implicit Models”, 2020
[11] A. Nichol et al., “Improved Denoising Diffusion Probabilistic Models”, 2021
[12] E. Hoogeboom et al., “Argmax Flows and Multinomial Diffusion: Learning Categorical Distributions”, NeurIPS2021
[13] Z. Kong et al., “DiffWave: A Versatile Diffusion Model for Audio Synthesis”, ICLR2021
[14] A. Radford et al., “Learning Transferable Visual Models From Natural Language Supervision”, 2021
[15] A. Ramesh et al., “Hierarchical Text-Conditional Image Generation with CLIP Latents”, 2022
[16] A. Nichol et al., “GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models”, 2022
[17] A. Ramesh et al., “Zero-Shot Text-to-Image Generation”, 2021
[18] C. Saharia et al., “Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding”, 2022
[19] M. Janner et al., “Planning with Diffusion for Flexible Behavior Synthesis”, ICML2022
[20] R. Huang et al., “FastDiff: A Fast Conditional Diffusion Model for High-Quality Speech Synthesis”, 2022
[21] E. Nachmani et al., “Zero-Shot Translation using Diffusion Models”, 2021
[22] J. Ho et al., “Classifier-Free Diffusion Guidance”, NeurIPS2021