はじめに
「ランダムフォレストはバギングの応用」というフワッとした理解から, もう1歩成長したいという人へ向けてこの記事を書きたいと思いました。偉そうにこんなことを言う私も, つい最近までランダムフォレストについては詳しくは知りませんでした。そこで, ランダムフォレストのアルゴリズムについて学習をしました。 ここでは, 私が学習した内容をなるべく丁寧に解説していきたいと思います。また, この記事では理論の説明だけでなく, pythonによる簡単な実装例についてもご説明しますので, もしよろしければ最後までご覧ください。
決定木
ランダムフォレストについて理解するために, まずは決定木を説明します。決定木は大きく分けて「分類木」と「回帰木」の2種類があります。
$x=(x_1, \cdots , x_d)^T$:$d$次元特徴量ベクトル
$y$:目的変数
と以下では表します。複数のデータ点を扱う際には$x^i=(x^i_1, \cdots , x^i_d)$と上付き添え字$i$を用いて, 第$i$データ点を表すこととします。決定木と回帰木の主な違いは$y$が質的な離散変数なのか, 実数値なのかです。質的な離散変数であれば, 分類木となり, 実数値であれば回帰木となります。ただし, いずれも土台となる考え方は変わりません。この記事では, まず分類木について説明していきますが, 回帰木のお話になっても基本は変わらないという事を意識して, 読み進めてもらえるとよいと思います。
まずは, 分類木から見ていきましょう。以下の図でざっくりと決定木のイメージをつかめれば幸いです。
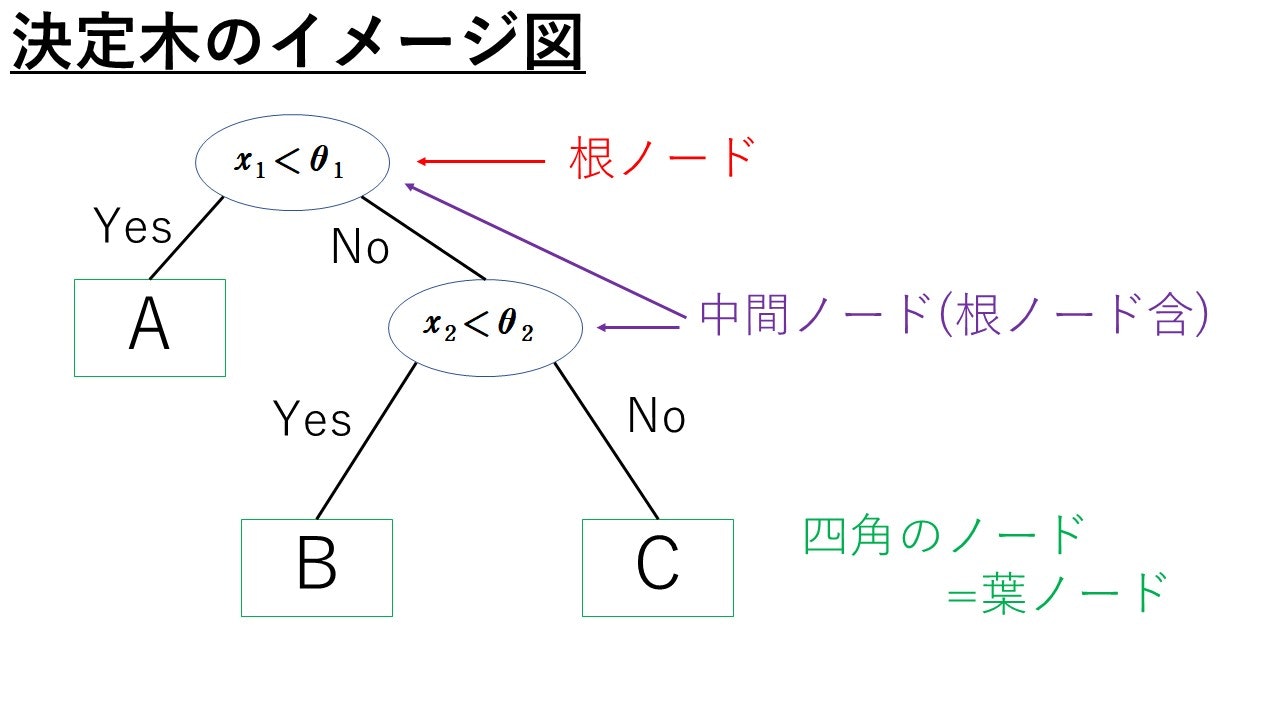
この図の決定木では, 以下の基準で分類を行います。
$A, B, C$という3つのクラスが存在する想定とし, データ点$x=(x_1, x_2) $について($d=2$として説明します),
(i) $x_1$がある定数$\theta _1$より小さければ, $x$はクラス$A$に分類される。
(ii) $x_1$がある定数$\theta _1$以上, かつ, $x_2$がある定数$\theta _2$より小さい, ならば$x$はクラス$B$に分類される。
(iii) $x_1 \ge \theta _1$かつ$x_2 \ge \theta _2$ならば, $x$はクラス$C$に分類される。
用語の紹介をしておきます。上の図において, 楕円と四角のことをノードといいます。特に, 楕円のノードを中間ノード, 四角のノードを葉ノードといいます。また, 一番上にあるノードは根ノードといいます。
ノードとノードを結ぶ線分を枝といいます。任意のノードに対して, そのノードから下に直接枝で結ばれたノードを子ノードといい, 逆に子ノードから見たときに, 元のノードのことを親ノードといいます。
上の例において, (i)~(iii)より$x_1x_2$平面を考えたときに, 決定木が描く決定境界は軸に対して垂直になります。上図の決定木の決定境界は下図のようになります。青いところに属するデータ点は$A$に分類され, 緑のところに属するデータ点は$B$に分類され, オレンジのところに属するデータ点は$C$に分類されます。
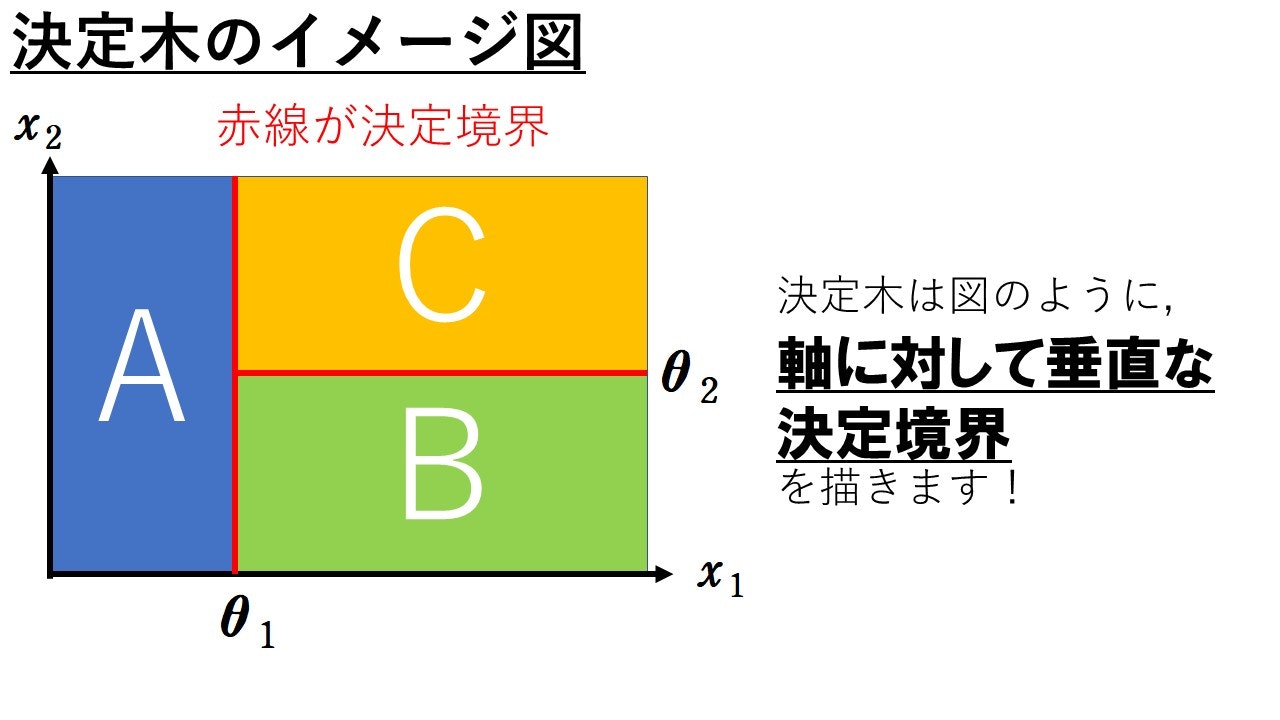
次に回帰木のざっくりとしたイメージをつかんでいきましょう!
とは, いったものの回帰木も分類木とほとんど変わりません。
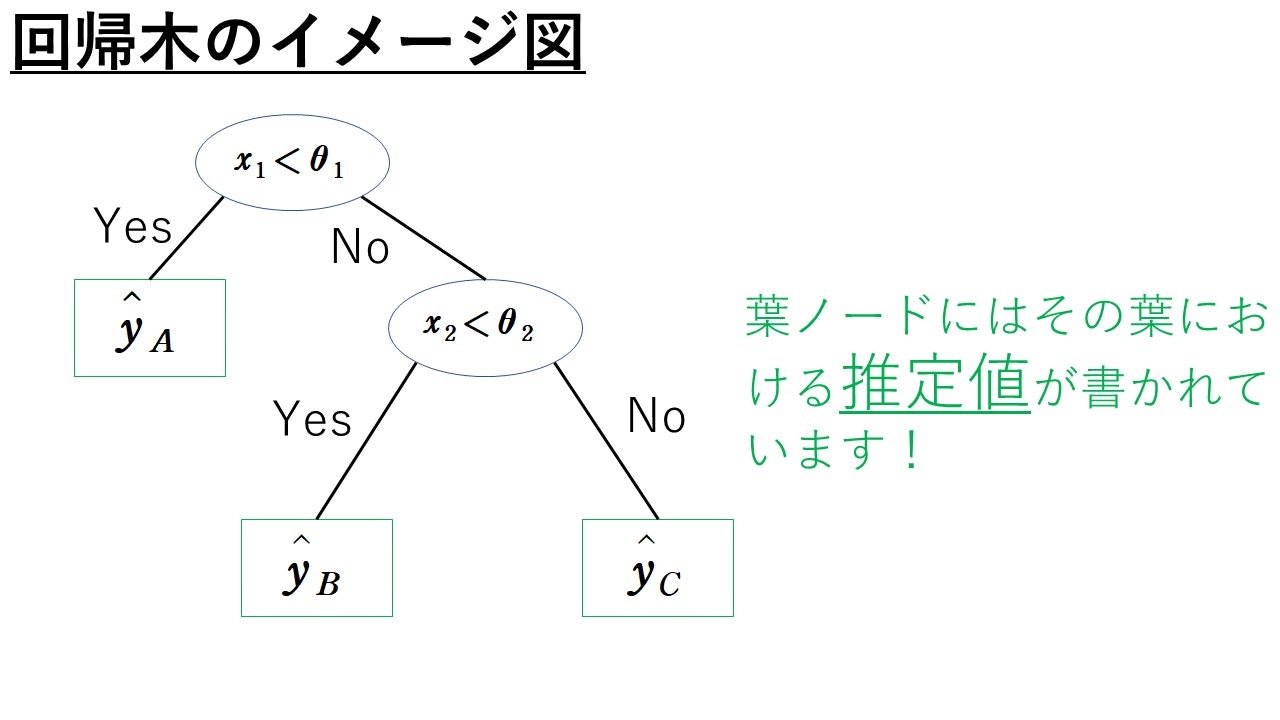
変わったのは, 各葉ノードに入っているのがクラスラベル$A, B, C$ではなく, 推定値$\hat{y}_A, \hat{y}_B, \hat{y}_C$となったことだけです。
決定木の学習
ここからは本格的に決定木の学習方法について説明していきます。決定木の学習にはID3やC4.5と呼ばれるものがありますが, ここではもっとも代表的なCARTと呼ばれる学習方法について紹介します。
(というより, 他の学習方法を学んだことがありませんのでご容赦ください(笑))
分類木の学習
まずは分類木の学習方法について説明します。先に登場する記号や指標の定義を述べ、最後にCART学習アルゴリズムを紹介します。
準備
$n$個の学習データ$(x^1, y^1), \cdots , (x^n, y^n)$が与えられており, 特徴量は$d$種類ある, すなわち, $x_i \in R^d$とします。
$M$種類のクラスラベル$c_1, \cdots , c_M$の集合を$C$で表します。今回は$d$個の特徴量を表現するために, それぞれの特徴量にインデックス番号$j$を振っておきます($j=1, \cdots , d$)。この$j$を属性番号といいます。
以上で, 記号の準備は完了です。ここからの目標は…
(目標1) 第$j$特徴量に対して, しきい値$\theta _j$を設定する。
(目標2) 各葉ノードに対してクラス$y\in C$を割り振る。
です。
各ノードには番号を割り振ることとします。根ノードのノード番号は1とします。ノード番号$r=1, 2, 3, \cdots$に対して, $I_r$を第$r$ノードに属する学習データの添え字集合とします。当然, 根ノードには$n$個すべてのデータ点が入ることになりますので$I_r=${$1, \cdots, n $}となります。今後, 第$r$ノードと$I_r$を同一視して, 第$r$ノードのことを$I_r$と呼びます。また, ノード$I_r$の中に属するデータ点の中で, クラスラベルが$y\in C$であるものの割合を$P(y|I_r)$と定義します。すなわち, $$P(y|I_r)=\frac{|\{i \in I_r:y_i=y\}|}{|I_r|}$$と定義する。ただし, 集合$A$に対して$|A|$は$A$に属する集合の要素の個数を表します。このとき, ノード$I_r$の不純度と呼ばれる指標を$\mathscr{I}(I_r)$で表します。不純度の定義には有名なものがいくつかあります。ここでは3種類ほど紹介します。
- エントロピー$$\mathscr{I}(I_r)=-\sum_{y\in C}P(y|I_r)(\log _2P(y|I_r))$$
- Gini関数$$\mathscr{I}(I_r)=1-\sum _{y\in C}(P(y|I_r))^2$$
-
誤分類率$$\mathscr{I}(I_r)=1-\max _{y\in C}P(y|I_r)$$
いずれの不純度も不純度という言葉から受ける印象通り「ノード内のデータ点のクラスラベルのの混ざり具合」を表す指標となっています。特定のクラスラベルのデータ点ばかりが1つのノードの中にあれば, そのノードの不純度は低くなります(0に近い値になる)。逆に, どのクラスラベルも均等に1つのノードの中にあれば不純度は大きな値をとります。(このことの雰囲気をつかみたければ, クラスが$c_1$と$c_2$のみの2値分類と考えてみましょう。いずれの不純度も「$P(y_1=c_1|I_r)=P(y_1=c_2|I_r)=0.5$のときに最大値をとり, $P(y_1=c_1|I_r)=1, P(y_1=c_2|I_r)=0$のとき0となる」ことを手計算で確認できます。)
さて, 分類木の学習で成し得たいことは, 当然ですが, 正しく分類することです。ということは, 不純度は低いほうが嬉しいわけです。ですので, 実は上で述べた(目標1)は「不純度が最も小さくなるようなしきい値$\theta _j$を探す」という問題に言い換えることができます。そこで, ノード$I_r$と属性番号$j$としきい値$\theta _j$に対して, $P_L(I_r, j, \theta _j)$を次のように定義します。
$$P_L(I_r, j, \theta _j)=\frac{|\{ i\in I_r:x^i_j <\theta _j\}|}{|I_r|}$$これは, ノード$I_r$に属するデータ点のうち「(第$j$特徴量)$<\theta _j$」を満たすものの割合を表しています。これに対して, $I_r$に属するデータ点のうち「(第$j$特徴量)$<\theta _j$」を満たさないものの割合を$P_R(I_r, j, \theta _j)$と定義します。すなわち,
$$P_R(I_r, j, \theta _j)=1-P_L(I_r, j, \theta _j)$$と定義します。(ちなみに, 添え字の$L$はLeft, $R$はrightの略です。ノードが左右に分割されるイメージに由来しているのかと思います。)このとき, 分割指数$G(I_r, j, \theta _j)$を次で定義します。
$$G(I_r, j, \theta _j)=\mathscr{I}(I_r)-P_L(I_r, j, \theta _j)\mathscr{I}(\{i\in I_r:x^i_j<\theta _j\})-P_R(I_r, j, \theta _j)\mathscr{I}(\{i\in I_r:x^i_j\ge\theta _j\})$$右辺の引き算する式
$$P_L(I_r, j, \theta _j)\mathscr{I}(\{i\in I_r:x^i_j<\theta _j\})+P_R(I_r, j, \theta _j)\mathscr{I}(\{i\in I_r:x^i_j\ge\theta _j\})$$は$\theta _j$をしきい値として, ノード$I_r$を分割してできた2つの子ノードの不純度の平均値(期待値)を表しています。そうすると$G(I_r, j, \theta _j)$は「$\theta _j$をしきい値として, ノード$I_r$分割した際の、不純度の平均的な減少量」を表していると解釈できます。したがって, この分割指数$G(I_r, j, \theta _j)$が大きいほど, 不純度が減少するようなしきい値$\theta _j$を選択できている, と捉えることができます。なので, ノード$I_r$に対して,
$$\theta ^*_j = \arg\max _{\theta _j}G(I_r, j, \theta _j)$$と定義し
$$j_r = \arg\max _{j}G(I_r, j, \theta _j^*)$$と定め, さらに
$$G=G(I_r, j_r, \theta _{j_r}^*)$$
と定義します。複雑に見えますが, ざっくり述べると$\theta _j^*$と$j_r$はノード$I_r$における分割指数$G(I_r, j, \theta _j)$を最大にする属性番号としきい値です。ですので, $G$はノード$I_r$における分割指数の最大値といえます。これらを踏まえるとノード$I_r$では, 属性番号$j_r $で,
しきい値$\displaystyle \theta _{j_r}^*$を選べばよいということになります。
これで一件落着…といいたいところですが、まだやることがあります。それはどのノードを分割するかの判断です。直感的には「不純度が高いところを分割すればいいじゃん!」と思うところですが、この考え方だと重要な要素が1つ抜け落ちてしまっています。それは各ノードに所属するデータ点の個数です。極端な例を挙げると、データ点がかなり少なくなっているノード$I_r$とまだデータ点がたっぷり入っているノード$I_s$とで、2つのノードがあったとします。不純度を比較した結果、ほんの少しだけ$I_r$の方が不純度が高かったとします。この状況下で分割を進めたいノードは$I_r$といえるでしょうか。答えはNoですよね。そこで、分岐選択基準$F_r$を以下で定義します。
$$F_r=G_r\frac{|I_r|}{|I_1|}$$これは不純度にデータ点の個数の割合をかけることで, 不純度に重みづけをした指標となっています。この値を用いて分岐するノードの選択を行います。
説明が長くなってしまいましたが、以上を踏まえていよいよCART学習アルゴリズムを紹介します。
CART学習アルゴリズム
$\mathscr{N}_{leaf}$で葉ノードの集合を表すこととします。
- 根ノードの番号を1とし, 初期値として$\mathscr{N}_{leaf}=\{ 1 \} , N=1$とする。学習データ点$x^i (i=1, \cdots , n)$の添字集合を$I_1=\{ 1, \cdots , n \}$と設定する。この上で$\theta _j^*, j_1, G_1 = F_1$を計算する。$F_1$の定義から, $G_1$と一致しますよね!)
- $r$を次のように決定する。$$r=\arg \max_{s\in \mathscr{N}_{leaf}}F_s$$(要するにこれは, 分割最大基準が最大である葉ノードを選んでいる訳です。)このようにして選んだノード$I_r$を以下の性質をもつように2つのノードに分割します。ただし, $r_L=N+1, r_R=N+2$です(この2式は, 新たに生まれるノードに, これまでとかぶりが無いように番号を振っているだけです。混乱しないようにしましょう!)。
$$
I_{r_L}=\{ i\in I_r:x_{ij_r} < \theta ^*_{j_r} \}
$$
$$I_{r_R}=\{ i\in I_r:x_{ij_r} \ge \theta ^*_{j_r} \}$$
また, $N = N+2$と更新する。加えて, $\mathscr{N_{leaf} = (N_{leaf}} {\bigcup} \{r_L, r_R\})\backslash \{r\}$ と更新しておく。
3. $r=r_L$として$\theta^*_j, j_r, G_r, F_r$を計算する。同様に, $r=r_R$でも計算する。
4. もし
$$
\max _{r\in \mathscr{N} _{leaf}}|I_r| \le S _{\min}
$$
が成立すれば分割を終了する。ただし, $S _{\min}$はあらかじめ自分で設定する値である。$S _{\min}$は葉ノードに含まれる最大の要素数である。
5. 各葉ノードに対して予測ラベル$\hat{y} _r \in C$を次のように割り当てる。
$$
\hat{y} _ r = \arg \max _{y\in C} P(y|I_r)
$$
以上がCARTの学習アルゴリズムです!
回帰木の学習
さて、ここからは回帰木について学習を進めていきましょう。いきなり煽るようで申し訳ないですが、ここまで乗り越えたあなたならば回帰木は簡単です!なぜならば、ほとんど分類木と学習方法が変わらないからです。なので、ここでは分類木との変更点に焦点をあてて説明します。
まず, 任意のノード$I_r$における算術平均を$\bar{y}_r$で表します。つまり,
$$
\bar{y}_r = \frac{1}{|I_r|} \sum _{i\in I_r} y_i
$$
このとき, 回帰木における不純度を以下で定義します。
$$
\mathscr{I} (I_r) = \frac{1}{|I_r|} \sum _{i \in I_r} (y_i - \bar{y}_r)^2
$$
そして, 回帰木のノード$I_r$における目的変数の推定値$\hat{y}_r $は
$$
\hat{y}_r = \bar{y}_r
$$
とします。要するに, 回帰木では不純度を平均2乗誤差に変えただけなのです。したがって, この不純度を小さくするように属性番号$j$と$\theta _j$の選択基準を考えることとなります。しかしながら、これは分類木のときと同様に考えれば解決します。もっと具体的に述べると, 分類木のときと同様に$G( I_r, j, \theta _j), G_r, F_r$を定義してあげればよいのです。ちなみに, 平均2乗誤差を不純度に用いた時の$G( I_r, j, \theta _j)$は尤離度と呼ばれています。
以上をまとめると, 分類木からの変更点は以下の2点だけです。
- 不純度を平均2乗誤にする。
- 予測値を$\hat{y}_r = \bar{y}_r$とする。
この2点だけ意識すれば, あとは分類木と同じです。
ランダムフォレスト
いよいよランダムフォレストのアルゴリズムについて解説していきたいと思います。ただし, ランダムフォレストについて学習するためには, ちょっとだけ前提知識が必要です。それは「バギング」です。以下の記事でアンサンブル学習やバギング, アダブーストについて, 数学的に詳しく解説しました。まだ勉強したことがなければ, 先にご覧ください。
【アンサンブル学習を丁寧に解説】バギングとアダブーストの仕組みも解説します!!
ざっくり述べると, ランダムフォレストとは複数個の決定木$T_1, \cdots , T_m$をバギングして学習させるアルゴリズムです。(多分木をたくさん作るからフォレストなんでしょうね(笑))基本的なイメージは以下の図のような感じです。バギングが土台となっています。
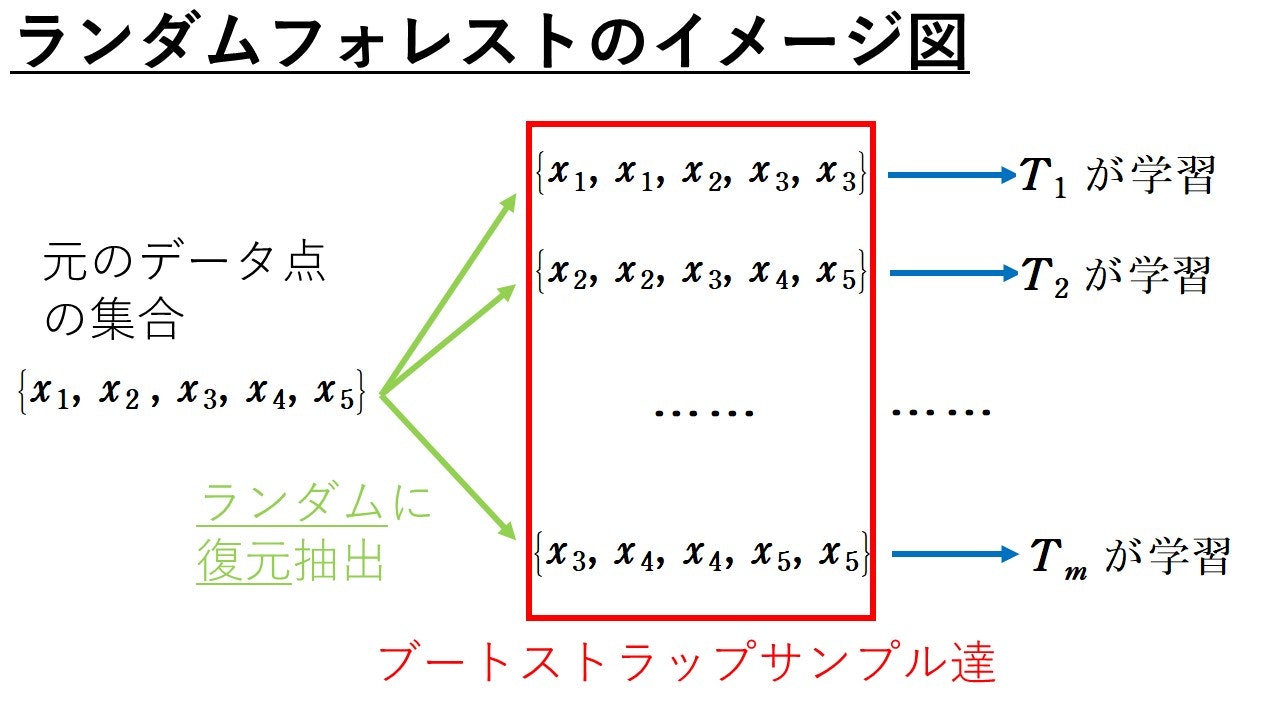
では、何が「ランダム」なのでしょうか。バギングについて学習された方は分かると思いますが、ランダムといわれる所以の1つはブートストラップサンプルを使っていることです。しかし, ランダムと言われる理由はこれだけではありません。もう1つだけランダムに決定するものがあります。それは, 各決定木を成長させるのに用いる属性番号$j$(特徴量)です。ランダムフォレストで用いられる決定木は属性番号$j$をランダムに選択して成長していくのです。それ故, 各々の決定木の成長の仕方が異なるため、過学習が生じないと言われています。
そろそろランダムフォレストのアルゴリズムについて紹介したいところですが, その前に記号使いについて説明しておきます。
$\mathfrak{B_1, \cdots , B_B}$:$B$組のブートストラップサンプル達
$J_r$:ノード$I_r$でランダムに選ばれた$m$個の属性番号の集合
以上を踏まえて, ランダムフォレストの説明をするときは$j_r$を
$$
j_r = \arg \max _{j\in J_r} G(I_r , j, \theta ^* _{j})
$$
と定義し直しておきます。すなわち, " ランダムに選択した "属性番号の中から分割指数を最大にする属性番号を$j_r$としました。
以上の記号使いを踏まえると, ランダムフォレストの学習アルゴリズムは以下のようになります。
ランダムフォレストのアルゴリズム
- $m$の値を設定する。(これはハイパーパラメーターなので自分でチューニングすることになります。絶対的な基準ではないですが, 分類問題では$m=[\sqrt{d}\ ]$, 回帰問題では$m=[\frac{d}{3}]$がよいなどといわれています。あくまで参考までに。)
- $B$組のブートストラップサンプル$\mathfrak{B_1, \cdots , B_B}$を生成する。
- 各$\mathfrak{B_i} \ (i=1, \cdots , B)$に対して, CART学習アルゴリズムを適用し, 決定木を成長させる。ただし, このとき$j_r$は上で再定義したものを用い, 属性番号は$|J_r|=m$となるようにランダムに選択する。
ランダムフォレストの学習アルゴリズムは以上です。では, ランダムフォレストではデータ点$x$に対して, 予測値をどのように求めるのでしょうか。ここからはそのことを説明していきます。
分類問題から説明していきましょう。もっとも単純な方法は各決定木の多数決です。ですが、単なる多数決を改良した方法が存在し、そちらの方がよく用いられていますので、ここではその方法を解説していきます。データ点$x$を決定木$T$に対して入力したときに, クラス$y$の推定確率を$P(y|T, x)$と表すこととします。このとき, $P(y|T, x)$の値を
$$
P(y|T, x)=P(y|I_r)
$$
と定義します。($P(y|I_r)$は決定木の説明で定義したものです。)ただし, $I_r$は決定木$T$に$x$を入力したときに, 最終的にたどり着く葉ノードとします。ランダムフォレストを構成する$B$個の決定木の集合を$\mathscr{T}$で表すこととします。このとき, ランダムフォレストがデータ点$x$のクラスラベルを$y$と推定する確率$P(y|x, \mathscr{T})$を次で定義します。
$$
P(y|x, \mathscr{T} ) = \frac{1}{B} \sum _{i=1}^{B} P(y|T_t, x)
$$
この式を最大にするような$y$を$x$に対する推定クラスとすればよいのです。
次に, 回帰の場合の説明をします… が, 考え方はほとんど分類と同じです。データ点$x$に対する決定木$T$の目的変数の推定値を$\hat{y} (x, T)$と表すこととします。このとき, ランダムフォレストによる目的変数の推定値$\hat{y} (x, \mathscr{T})$を次のように定義すればOKです。
$$
\hat{y} (x, \mathscr{T}) = \frac{1}{B} \sum _{i=1}^{b} \hat{y}(x, T_i)
$$
Out Of Bag(OOB)データを用いた推定誤差の測定
ここからは, 少しお話が変わりましてランダムフォレストの誤差の推定値について説明していきます。ランダムフォレストでは, テスト用のデータを用意しなくても推定誤差を図る方法が存在します。そのために, まずはOOBデータについて説明します。
各ブートストラップサンプル$\mathfrak{B_i}$は$n$組の学習データ$(x_1, y_1), \cdots , (x_n, y_n)$から" 重複を許して "$n$個のデータを" 復元 "抽出して作られています。それ故, $\mathfrak{B_i}$を作るのに利用されていない学習データが存在しますよね。この利用されなかったデータを$\mathfrak{B_i}$のOOBデータといいます。ということは, 決定木$T_i$の性能を確認するために, $\mathfrak{B_i}$のOOBデータを利用することができるわけです。ここで, 各学習データ$(x_k , y_k)$に対して, $A_k$を次のように定義します。
$$
A_k = \{ i \in \{ 1, \cdots , B\} :(x_k, y_k) \notin \mathfrak{B_i} \}
$$
すなわち, 各$k=1, \cdots ,n$に対して$(x_k, y_k)$を含まないブートストラップサンプルの添え字集合を$A_k$と定義しました。この記号を用いて推定誤差の計算を説明します。まずは, 分類問題から説明していきます。$x_k$が与えられたときのクラス$y$に対するOOB推定確率を次式で定義します。
$$
\tilde{P} (y|x_k, \mathscr{T} ) = \frac{1}{|A_k|} \sum _{i \in A_k} P(y|T_i, x_k)
$$
上式は, 各決定木の予測平均ですね。このとき, 学習データ$x_k$に対する予測クラス$\hat{y} (x_k, \mathscr{T} )$を
$$
\hat{y} (x_k, \mathscr{T} ) = \arg \max _{y \in C} \tilde{P} (y|x_k , \mathscr{T})
$$
と定義します。つまり, 各決定木の予測平均が最も高くなるような, クラスラベル$y$を予測値として返します。このことを踏まえると, 分類問題に対するランダムフォレストの推定誤差$\hat{P} _{err}$は次式で定義します。
$$
\hat{P} _{err} = \frac{| \{ k \in \{ 1, \cdots , n \} : y_k \neq \hat{y} (x_k, \mathscr{T} )\} |}{n}
$$
これは誤分類されたデータ点の平均個数ですね。
つぎに, 回帰問題の推定誤差について説明します… がもう予想がついているかと思いますがやはりほとんど同様です(笑)学習データ$x_k$が与えられたときのOOB推定値$\hat{y} (x_k, \mathscr{T} )$は
$$
\hat{y} (x_k, \mathscr{T} ) = \frac{1}{|A_k|} \sum _{i \in A_k} \hat{y} (x_k, T_i)
$$
と定義し, 推定誤差は
$$
\hat{E} _{MSE} = \frac{1}{n} \sum _{k=1}^{n}(y_k -\hat{y} (x_k , \mathscr{T}))^2
$$
と定義します。
特徴量重要度
記号の説明
ランダムフォレストを用いると特徴量重要度なる, 読んで字のごとく特徴量の重要性を表す1つの指標が与えられます。その計算アルゴリズムを説明するために, 登場する記号使いを紹介しておきます。
各決定木$T_i \ (i=1, \cdots , B)$に対して,
$\mathscr{N_{inter}^{i}}$:決定木$T_i$に対する中間ノードのノード番号全体の集合
$F_r ^i$:決定木$T_i$のノード$I_r$における分割選択基準
$D_j$:属性番号が$j$である特徴量の重要度(これから求めたいものです!)
では, $D_j$の算出アルゴリズムをみていきましょう。
特徴量重要度を算出するアルゴリズム
- $j=1, \cdots , d$に対して$D_j = 0$と初期化する。
- すべての$i=1, \cdots ,B$に対して次の計算を行う。
決定木$T_i$におけるすべての$r \in \mathscr{N_{inter}}$に対して, $D_{j_{r}}$を次式で更新していく。
$$
D_{j_{r}}=D_j +F^i_r
$$
(ここで注意してほしいことは, 更新されない($D_j=0$のまま)属性番号$j$も存在することです。どの決定木のどの中間ノードでも$j_r$として選ばれなかった属性番号は重要度が更新されることなく0のままとなります。) - 各$j=1, \cdots , d$に対して, $D_j$を
$$
D_j = \frac{D_j}{B}
$$
で更新し, この値を属性$j$の重要度として出力する。
このアルゴリズムを考察します。最終的に出力される$D_j$は, 各決定木$T_i$とその決定木での分岐選択基準$F^i_r$の総和を$B$で割った値です。そして, 分岐選択基準を定義するために用いられた$G_r$というのは, ノード$I_r$における不純度の減少量でした。ということは, 最終的に出力される特徴量重要度$D_j$とは属性番号が$j$である特徴量が, 不純度の減少に平均的にどれほど寄与したのかを表す値と捉えることができます。なので, 分類問題においては誤分類率の減少, 回帰問題においては平均2乗誤差を小さくするような特徴量はどれなのかということをみる1つの指標となります。
部分依存グラフ
分類問題についてお話しします。ある特徴量に注目したときに, その特徴量が分類にどのように影響を与えるのかを可視化する方法として部分依存グラフというものがあります。グラフは最後の実装のところで, 実際に書いたものをお見せします。まず先にどんな関数のグラフを書くのかを説明しちゃいます。各学習データ$x^{i}$に対して, 属性番号が$j$である特徴量の値を変数$t$で置き換えた学習データ点を$x^{i,j}(t)$と表すこととします。クラスラベル$y_0\in C$に対して, 関数$f^{y_0,\ j}(t)$を次で定義します。
$$
f^{y_0,\ j}(t) = \sum _{i=1}^n \{ \log P(y_0|x^{i,j}(t), \mathscr{T}) -\frac{1}{|C|} \sum _{y\in C} \log P(y|x^{i,j}(t), \mathscr{T}) \}
$$
この関数の$i$に関する和の中身の式は, よーく見ると, $\log P(y|x^{i, j}(t), \mathscr{T})$の$y_0 \in C$に関する偏差となっています。なので, この偏差が大きくなればなるほど$y_0$に分類される確率が高いと捉えることができるわけです。そして, この偏差を$i$について和をとっているため, 各データ点の$y_0$への分類のされやすさの合計と捉えることができます。以上を踏まえたうえで意識してほしいことは, この関数の変数は$t$であることです。ということは, $f^{y_0,\ j}(t)$は変数$t$を動かしたときに(属性番号が$j$の特徴量が変化したときに), $y_0$への分類のされやすさの変化を表現した関数と捉えることができます。
ランダムフォレストの簡単な実装例
ランダムフォレストの理論に関する説明は以上で完了となります。ここからは, 簡単な実装例について紹介したいと思います。
扱うデータはコチラです。
https://www.kaggle.com/kemical/kickstarter-projects
ざっくり述べると様々なプロジェクトに関するデータが入っており, それらのプロジェクトは成功したのか失敗したのか、はたまたその他の事情なのか, などを分類する問題です。
前処理の内容
ここでは, ランダムフォレストの実装に焦点をあてたいので前処理についてはざっくりとだけ説明しておきます。目的変数であるstateについては何種類かありますが, 説明のしやすさのために成功, 失敗の2つにしぼり2値分類問題にしています。プロジェクト名については単に文字数や単語数に変換して, 数値データになおしています。日付データに関しては, 少しだけいじってプロジェクトが実施された日数、月、四半期などの特徴量を作っております。皆さん色々試してくださいませ(笑)1つだけ指摘しておきますと, backerなどはプロジェクトが完了してから集計される値なので, 実際の分析では利用できません。こういった特徴量は抜いて挑戦すると面白いかもです。
いよいよ実装
from sklearn.ensemble import RandomForestClassifier
# testデータとtrainデータの作成
X = df.drop(columns=['state'], inplace=False)
y = df['state']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# ランダムフォレスト分類器の学習と予測
RFC = RandomForestClassifier(n_estimators=100, oob_score=True, random_state=0)
RFC.fit(X_train, y_train)
y_pred = RFC.predict(X_test)
ooc = RFC.oob_score_
これでランダムフォレストの予測は完了です。RandomeForestの引数のn_astimatorsは決定木の個数を指定しています。ooc_scoreはデフォルトがFalseなのですが, 上のようにTrueにしてあげればOOBデータを用いた推定誤差を計算することが可能になります。他にも様々な引数があります。各決定木の最大ノード数を指定するmax_leaf_nodes, 上で説明した$S_{min}$に対応するmin_samples_splitなどもあります。以下で分かりやすくまとめてくれているのでぜひ見てみてください!
https://data-science.gr.jp/implementation/iml_sklearn_random_forest.html
また, OOBデータを用いた推定誤差は上のようにoob_score_で計算できます。
from sklearn.metrics import roc_auc_score
from sklearn.metrics import accuracy_score
print('ooc_score', ooc)
print('accuracy:' , accuracy_score(y_true=y_test, y_pred=y_pred)*100)
print('roc_auc: ', roc_auc_score(y_true=y_test, y_score=RFC.predict_proba(X_test)[:,1]))
上のコードでそれぞれスコアを確認してみます。実行結果は以下の通りです。
ooc_score 0.6783634546801509
accuracy: 68.56376189662623
roc_auc: 0.7390866098486356
まぁまぁですね(笑)
特徴量重要度
以下のコードで特徴量重要度を可視化できます。
feature_name = X.columns
importances = RFC.feature_importances_
indices = np.argsort(importances[:10])
plt.barh(np.array(feature_name)[indices], importances[indices],
color='r', align='center')
plt.show()
上のコードでは重要度が高いものtop10を表示しています。
実行結果は以下の通りです。
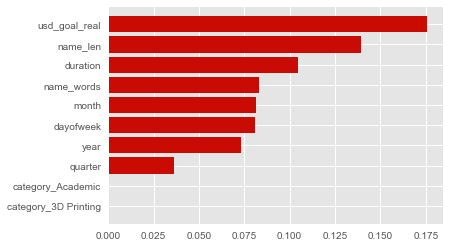
部分依存グラフを書く
def pdplot(model, df, feature, target=1):
"""
部分依存グラフ(Partial dependence plots))を書く!
model:モデル、今回はもちろん上で作成したRFC
df:利用するデータフレーム
feature:横軸に利用したいカラム名
target:注目したい目的変数と対応するindex番号(以下のコードを見た方が分かるかも)
"""
df_ = df.copy()
x = list()
y = list()
# 対象の特徴量の最小値から最大値までに0.1刻みのnumpy配列を作成
seq_list = np.arange(np.min(df[feature]), np.max(df[feature]), 0.1)
for seq in seq_list:
# 対象の特徴量の値を書き換える
df_.loc[:, feature] = seq
# 各データ点に対する所属確率を計算して, その対数を計算
# クラス所属確率が0の場合にエラーがでちゃうのでlog1pを使用
pred_list = np.log1p(model.predict_proba(df_))
sum_pred_prob = 0
# このfor文でiに関するシグマを計算します
for pred in pred_list:
# クラス所属確率の対数の和
# 今回は2値分類なのでlen(pred)=2
sum_log_prob = np.sum([pred[k] for k in range(len(pred))])/len(pred)
#ここでtargetを利用。今回の場合は, デフォルトのtarget=1にすれば, successと対応する確率に注目する
sum_pred_prob += (pred[target] - sum_log_prob)
x.append(seq)
y.append(sum_pred_prob)
plt.plot(x, y)
plt.xlabel(feature)
plt.ylabel('partial dependence')
plt.title('Partial dependence plots')
このような関数を定義すると部分依存グラフが書けます!
ちなみにですが…
実は, sklearnにも部分依存グラフを書くためのライブラリが入っているようです。
https://scikit-learn.org/stable/modules/partial_dependence.html
私も実力不足なところがありsklearnの中身を完璧に理解しているわけではないのですが, 本記事でご紹介したものとは計算方法が少し違う印象です。ですので, pdplot関数を上のように定義して, 本記事で紹介した部分依存グラフの定義に従ってグラフを書いてみました。
では, 以下のコードを実行して部分依存グラフを作成してみましょう。
df_pdplot = pd.DataFrame(X_train, columns=X_train.columns)
pdplot(RFC, df_pdplot, 'name_len', target=1)
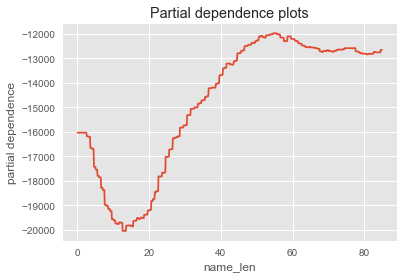
name_lenというのはプロジェクト名の文字数です。このグラフを見るとあまりにもプロジェクト名が短いと(特に20文字を下回ると)失敗に分類される確率が高まるようですね。だからといって, 多ければよいと分析するのも安直ではありますが(笑)
とにかく!このようにして, 部分依存グラフはデータ分析に役立てることも可能です。
終わりに
かなり長い記事となってしまいましたが最後まで読んでくださりありがとうございました!
皆さんの勉強にお役立ちできたのであれば幸いです。
参考文献
平井有三 著「はじめてのパターン認識」
後藤正幸, 小林学 共著「入門 パターン認識と機械学習」