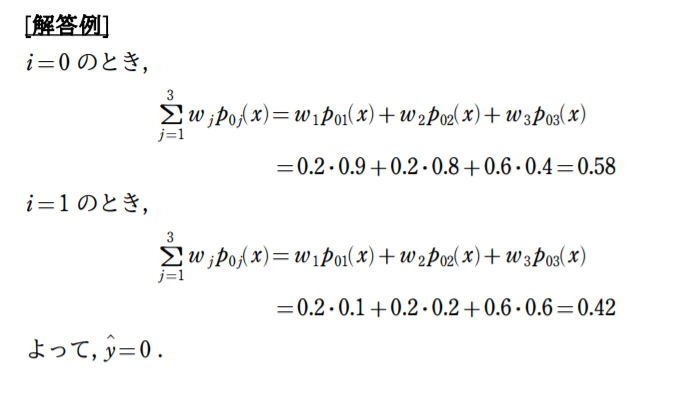この記事について
アンサンブル学習について「弱学習機を組み合わせることで、より優秀な学習機をつくるんだ!」ということは'何となく'分かっていました。ですが, アンサンブル学習をすると何がどう嬉しいのかということの理解が曖昧でした。そこで, アンサンブル学習がどのように嬉しいのかということを'数式で'理解したくなり勉強しました。本記事ではアンサンブル学習について数学的に理解したことをまとめたいと思います!
アンサンブルの基本
アンサンブル学習について以下の段階を追って話していこうと思います。
- シンプルな多数決アンサンブル
- 確率を考慮した多数決アンサンブル
- 重み付きシンプル多数決アンサンブル
- 重み付き確率を考慮した多数決アンサンブル
これらの話が終わった後に, バギングとアダブーストについてはお話ししします。
シンプルな多数決アンサンブル
分類問題を前提にお話を進めます。

これは一番シンプルなアンサンブル学習です。$mode$というのは最頻値を表します。要するに{ }の中身の数で一番個数が多いものを返す関数です。 $m$個の分類器を$C_1 , C_2, \cdots , C_m$とし、あるデータ点を$x$とします。各分類器が予測した$x$のクラスラベルを$C_i(x) \ (i=1, 2, \cdots , m)$で表すこととします。
一番シンプルな多数決アンサンブルでは$x$のクラスラベルを, 上の画像のように予測します…
とはいえ, これだけでは意味が分かりにくいと思いますので, 以下に具体例を用意しました。

この画像では, 3つの分類器$C_1, C_2, C_3$が$x$のクラスラベルを順に$1, -1, 1$と予測しています。この場合1が2票, $-1$が1票です。したがって, 3つの分類器をシンプルな多数決アンサンブルした結果$x$のクラスラベルの予測値$\hat{y}$は, 最も得票数の多い1となります。
確率を考慮した多数決アンサンブル
次は, 各分類器$C_1 , C_2, \cdots , C_n$が予測した'クラスラベル'ではなく'所属確率'を返す場合を考えます。例えば, 0か1かの2値分類をするタスクを考えるのであれば, データ$x$に対して,
$$C_1(x)=(0.3, 0.7)$$
のように各クラスに所属する確率を返します。(上の例だと$x$は0.3の確率でクラスラベルが0, 0.7の確率でクラスラベルが1と予測)この場合のアンサンブルの誤分類率は以下のように計算します。

ここで$k$は分類器の個数$n$が偶数であれば$k=\frac{n}{2}$, 奇数であれば$k=\frac{n+1}{2}$とします。(分かりにくく見えますが、シグマの中身は高校数学で習う「反復試行の確率」ですね)要するに上の式は, 半分以上の分類器が間違えちゃう確率を計算しています。ensembleの綴りが間違っている事には目をつむってください(笑)
ここで, 各分類器は互いに独立という仮定を設けていますが, これは説明のために設けただけです。独立でなければ上の式は成り立ちませんよね。実際に, 複数のモデルをアンサンブルするときに, すべてが完全に独立ということはそうそう起こらないと思います。同様にすべての分類器の誤分類率が$\epsilon$と等しくなっているのも, 説明の為に設けた過程でしかありません。実際は, そうはならないでしょう。
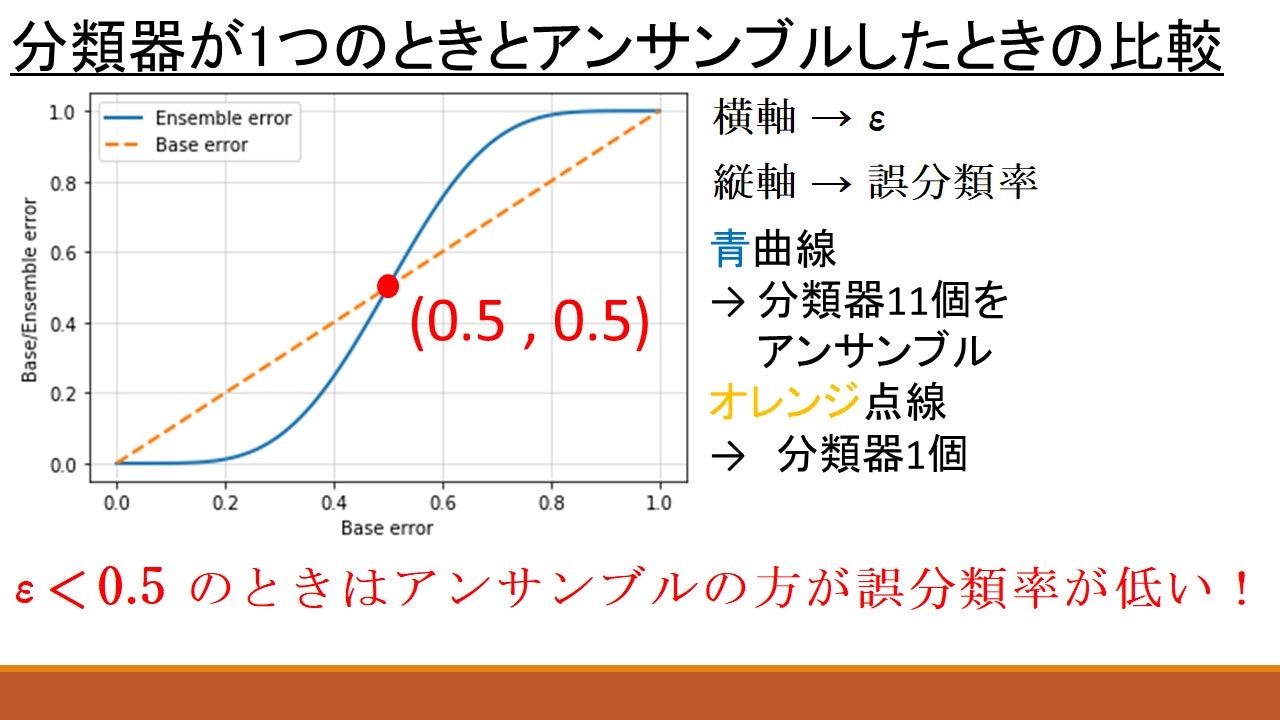
かなり都合の良い仮定を設けはしましたが, この仮定の下で上のグラフを見るとアンサンブルの良さが少しつかめるのではないでしょうか。上の青い曲線は, 誤分類率$\epsilon$の分類器を11個アンサンブルしたときの誤分類率$\epsilon _{ensemble}$の変化を表しています。オレンジの曲線は分類器が1つの場合の誤分類率を表しています。すると$\epsilon < 0.5$の範囲では, 常に青い曲線の方が下にあります。つまり, 数学的にはアンサンブルした方が誤分類する確率が低いということです。
重み付きアンサンブル~シンプル多数決編~

ここで, $A$はクラスラベルの集合です。$\chi$と$argmax$の意味を説明したいと思います。

まずは$argmax$です。これは上の画像で書いたように[ ]の中身を最大にするような$i$を返す関数です。上の例だと, $i^2+1$に$i=1$を代入すると$i^2+1=2$で, $i^2+1$に$i=-2$を代入すると$i^2+1=5$です。2と5の大小関係を比較すると, 大きいのは当然5なので, 対応する指数$i=-2$が返されています。

続いて, 特性関数の定義を紹介します。ざっくり述べると, ( )の中身が正しければ1, 正しくなければ0を返す関数です。(個人的にはLebesgue積分の構成でよくみる関数です。)$A$はクラスラベル全体の集合です。2値分類なら$A$の要素の個数は2個です。$A$の存在意義が薄く感じるかもしれませんが, 「$i$は$i \in A$を動く」ということが分かるように明示的に$A$が添え字に使われています。上の画像は, 分類器$C_1$があるデータ点$x$のクラスラベルを0と予測しているときの例を紹介しています。このとき, $C_1(x)=0$は正しいので, $\chi _A(C_1(x)=0)$は1となります。一方, $\chi _A(C_1(x)=1)$は, いま$C_1$は$x$のラベルを$0$と予測しているのにも関わらず( )の中身は$C_1(x)=1$になっています。それ故, ( )の中身が正しくないので$\chi _A(C_1(x)=1)=0$となります。
さて, 登場する記号をすべて紹介しましたので, 以下の問題に挑戦してみてください!
雰囲気をつかんでもらえると嬉しいです。
【解答例】
$i=0$のとき,
$$\sum _{j=1}^3w_j\chi _A(C_j(x)=0)=0.2\cdot1+0.2\cdot1+0.6\cdot0=0.4$$
$i=1$のとき,
$$\sum _{j=1}^3w_j\chi _A(C_j(x)=1)=0.2\cdot0+0.2\cdot0+0.6\cdot1=0.6$$
よって, $\hat{y} = 1$である。
解くことはできたでしょうか。この問題で計算のしくみをつかんでくれると嬉しいです。さて, 問題の結果を少し考察していきましょう。一番初めに紹介した, 重みを考慮しないシンプルな多数決の仕組みであれば, 問題の舞台設定だと$C_1(x)=0, C_2(x)=0, C_3(x)=1$で, 0が2票, 1が1票なので予測値は$\hat{y}=0$となっていたはずです。ところが, $(w_1, w_2, w_3)=(0.2, 0.2, 0.6)$という重みを各分類器に課したことで, 今回の問題では$\hat{y}=1$となりました。これが重みの影響です。$C_1$と$C_2$にかけられる重みが0.2であるのに対し, $C_3$には0.6もの重みがかけられています。0.2の3倍が0.6ですので, $C_1, C_2$に対して, 3倍も$C_3$の予測が強く影響するという事です。
確率を考慮した重み付きアンサンブル
ここまでくれば, 上の画像を見てどんな計算を行いたいのか分かるかと思います。各分類器が予測したクラスラベルではなく, 確率を返す場合を考えます。(上で説明した「確率を考慮した多数決アンサンブル」と同じ状況です)上の例の表の見方は, 分類器$C_1$があるデータ点$x$を「0.8の確率でラベルは0であり, 0.2の確率でラベルは1である」と予測したことを表しています。同様に, 分類器$C_2$についても, あるデータ点$s$を「0.6の確率でラベルは0であり, 0.4の確率でラベルは1である」と予測したことを表しています。
もう意味不明な記号は無いはずです。いきなりですが, 次の問題に挑戦してみましょう!
計算の仕組みをつかめるはずです。
問題を解くことはできたでしょうか。この問題においても, 先の問題と同様に重みが作用していますね。要するに, $C_3$の予測が$C_1, C_2$の予測よりも3倍影響しているということです。
以上で
- シンプルな多数決アンサンブル
- 確率を考慮した多数決アンサンブル
- 重み付きシンプル多数決アンサンブル
- 重み付き確率を考慮した多数決アンサンブル
の基本4パターンのアンサンブル学習の解説は終了です。次は, バギングとアダブーストの説明に移っていきます!
バギング
バギングと呼ばれるアンサンブル手法の1種を紹介していきます。バギングとはブートストラップサンプルなるデータを用いて, 複数の分類器を「並列的に」学習させる手法のことです。予測はこれらの分類器の多数決で行います。
ブートストラップサンプルとは何かを説明します。
以下の図のように, データ点の集合からランダムに復元抽出を行うことで, 新たに作り出したサンプルデータのことを指します。
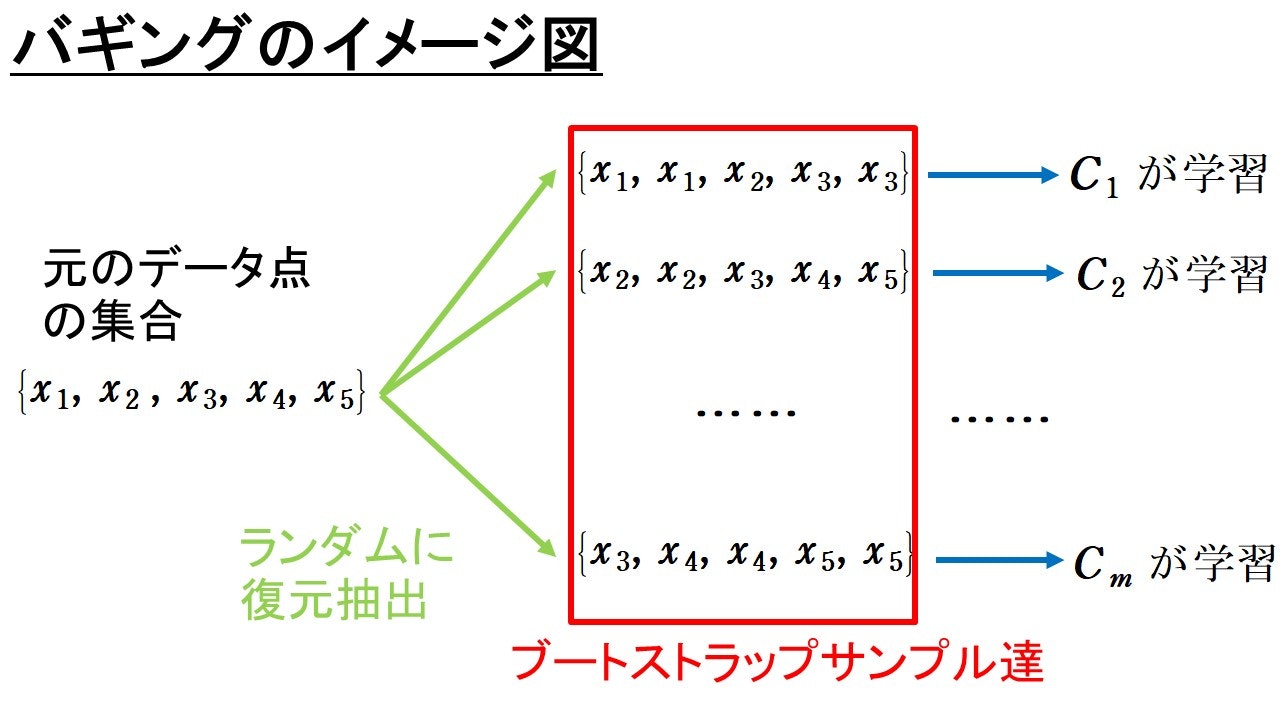
上図のようにして, 作り出したブートストラップサンプル達を使ってそれぞれの分類器を並列して学習させます。このようにして学習させた分類器達を多数決アンサンブルさせて予測値を求めるのが, バギングという手法になります。各分類器の学習に使われるサンプルが異なるため, 過学習を防ぎ, 未知のデータへの汎化性能の向上が期待されます。バギングの有名な応用例がランダムフォレストです。この記事では紹介しませんが併せて勉強してみてもよいかもしれません。
アダブースト
最後にアダブースト(adaptive boosting)について紹介します。それなりに数式が登場するので, 数学に苦手意識がある人は難しく感じるかもしれません。頑張りましょう!
まず, アダブーストについてざっくりと概要を述べます。アダブーストでは複数個の分類器$C_1, \dots ,C_m$を「直列的に」学習させます。ここでいう直列的とは, まず$C_1$の学習を行い, 各データ点に対応する重みを更新してから, 次の分類器$C_2$の学習を行うということです。この操作を繰り返すことで, 各分類器の学習を行うことを, 直列的と表現しています。( バギングは「並列的」と言いましたが, バギングではそれぞれの分類器が独立して学習を行っていましたよね。) アダブーストでは, 重みの更新の仕方が特徴的です。どのように更新するかというと, 誤った分類をされたデータ点と対応する重みの更新を大きく行い, 正しく分類されたデータ点と対応する重みの更新を小さく行います。
アダブーストの学習アルゴリズム
いよいよ数式による説明に移っていきます。上で説明したざっくりとしたイメージを大事にして読み進めてください。その方が理解がスムーズになると思います。
基本的にアダブーストは2値分類を行う際に利用する学習アルゴリズムです。もし, 多クラス分類に応用するのであれば, 1対他の分類器を作成する必要があります。
これからアダブーストの学習アルゴリズムを紹介しますが, 記号使いは以下の通りです。
$C_m:$異なる$M$個の分類器($m=1, 2, \cdots , M$)
$x_i:$異なる$N$個のデータ点($i=1, 2, \cdots , N$)
$y_i:$データ点$x_i$のクラスラベル。$1$か$-1$となる。
$w^m_i:$データ点$x_i$と対応する重み。$m$は何回目の更新かが分かるように書かれた添え字(累乗ではありません)
$\chi(\cdot):$特性関数, ()の中身が正しければ1, 正しくなければ0を返す関数
$sgn(\cdot):$符号関数, ()の中身が負ならば-1, 0ならば0, 正ならば1を返す関数
細かい説明は後で行いますが, まずは以下の学習アルゴリズムを考えながら読んでみてください。

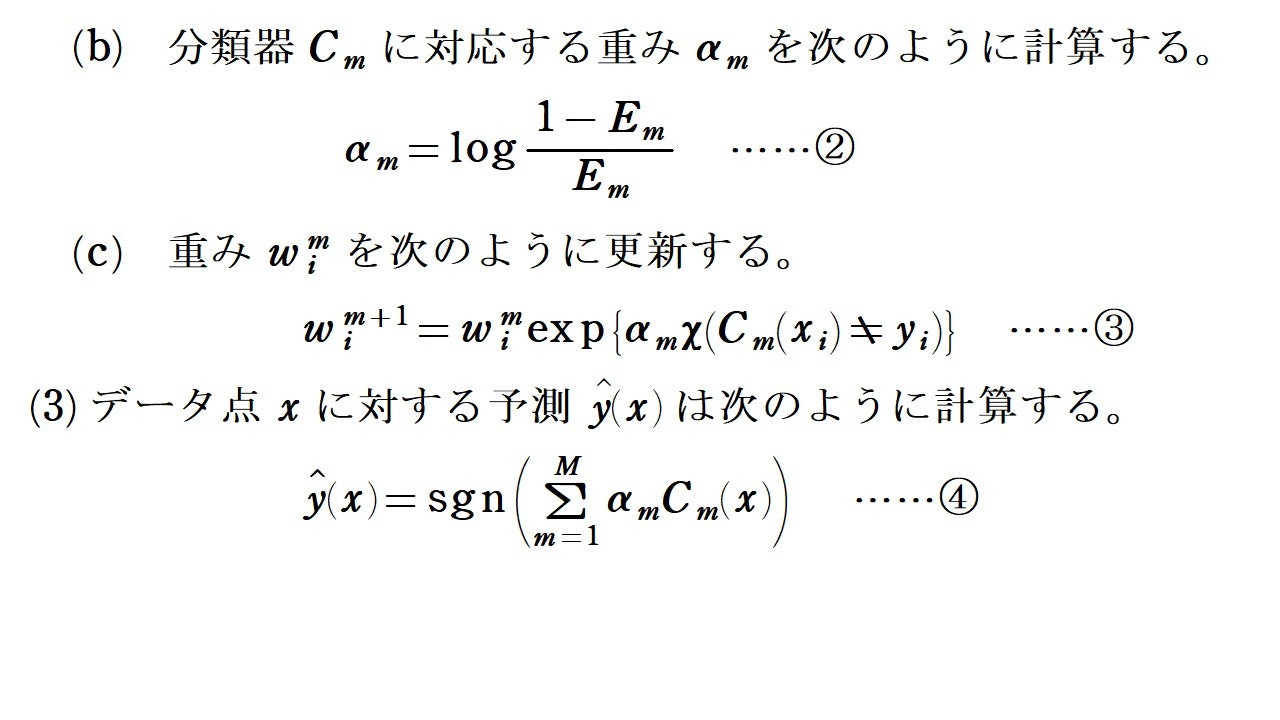
$E_m$については, 定義から0以上1以下ですが, 各分類器の誤分類率が$\frac{1}{2}$より小さければ(1つ1つの分類器の精度が低かったとしても半分以上間違うことはないという想定), $E_m<\frac{1}{2}$となることに注意してください。したがって, $$\frac{1-E_m}{E_m}=\frac{1}{E_m}-1>1$$なので, ②より, $\alpha _m>0$となります。また, 上の式から$\frac{1-E_m}{E_m}$は$E_m$が小さいほど大きくなることが分かります。故に②から, $\alpha _m$は, $E_m$が小さいほど大きくなるようになっています。
③と$\alpha _m >0$から, 重みの更新は各$i=1, 2, \cdots ,N$に対して, データ点$x_i$の予測を$C_m$が誤っていたとき(すなわち, $C_m(x_i)\neq y_i$のとき), $w_i^m<w_i^{m+1}$となるように更新されることが分かります。つまり, 分類器$C_m$が$x_i$の予測を誤ったとき, $x_i$に対応する重みが大きくなるように更新されることが分かります。誤っていないデータ点に関しては, $\chi (C_m(x_i)\neq y_i)=0$となり, 重みは全く変化しません。加えて, 手順(c)が完了し, 再び手順(a)へ戻るたびに, 式①により$E_m$が正規化されるので, 正しく分類されたデータ点に対する重みは「相対的に」小さくなっていくことに注意しましょう。
データ点$x$のラベルの予測方法は, ④の通り, 重みを考慮したシンプルな多数決となっています。分類器の個数$M$が大きすぎると過学習が生じ, 汎化性能が低下することもあるので, (調整が難しいところではありますが,)気を付ける必要があります。
アダブーストの学習アルゴリズムの導出
アダブーストの学習アルゴリズムは, 次で定義される指数誤差関数$E$を最小化するという考えのもと導出されます。
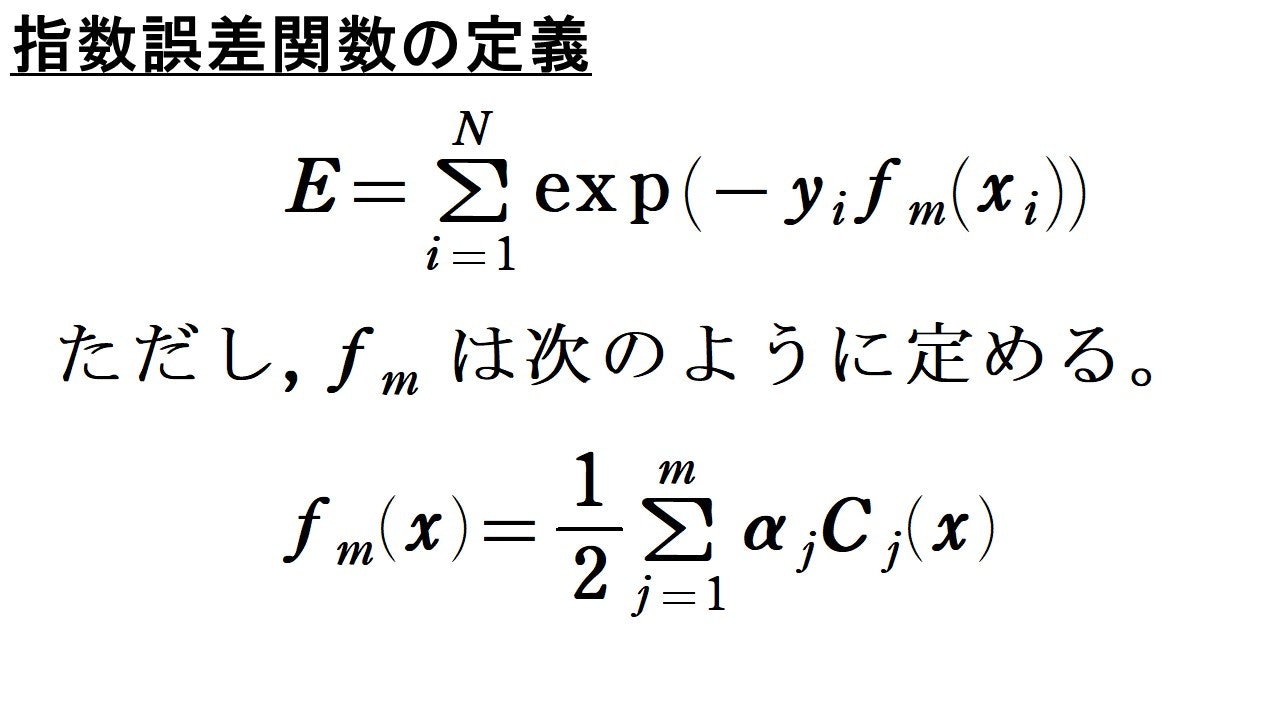
$E$について説明します。$f_m(x_i)$は$f_m$の定義から, 分類器$C_1, \cdots , C_m$が予測した$x_i$のクラスラベル$C_m(x_i)$の線形結合となっています。それ故, 誤分類した分類器の個数が多ければ, $-y_if_m(x_i)$の値が大きくなります。それ故, $E$を最小にするということを考えます。
$E$を最小化するとは言いましたが, 最小化は「逐次的に」行われるということに注意してください。逐次的とはどういうことか説明します。上の記号使いでは分かりにくいのですが$E$は$m$の値に依存して変化します。(このことは, $f_m$の定義を見れば分かります。)なので, $m=1$のときから$m=M$のときまで, 順に最小化していきます。このことを指して「逐次的」といっています。
それでは, 逐次的な$E$の最小化を考えていきましょう。
目的を見失わないようにしてください。逐次的に最小化を考えるので, 各$i=1, 2, \cdots , n$に対して, $C_1(x_i), C_2(x_i), \cdots , C_{m-1}(x_i)$と$\alpha _1, \alpha _2, \cdots , \alpha _{m-1}$の値は既に定まっているものとして考えます。この前提の下で, $C_m(x_i)$と$\alpha _m$の最適化を考えていきます。
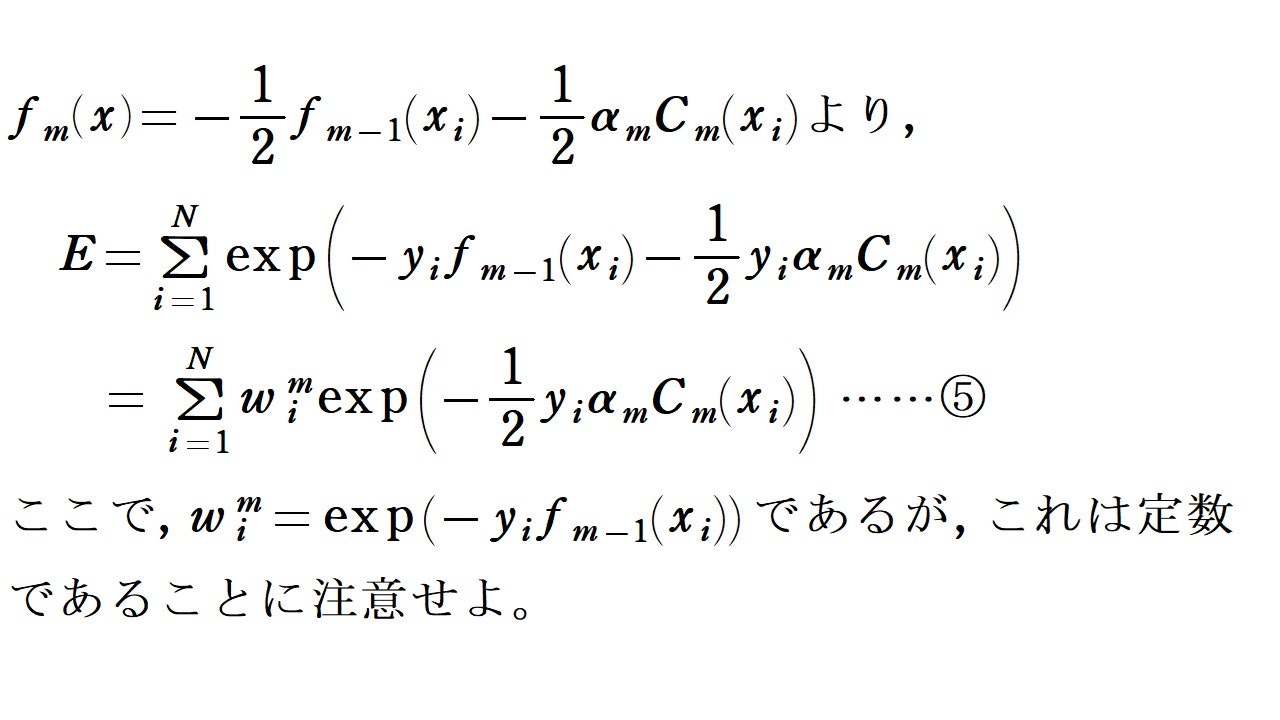
まず, 上の計算のように$E$を変形しました。逐次的に考えているので, ここでは$w_i^m$は定数です。
次に, $C_m$によって正しく分類されたデータ点の添字集合を$T_c$, 誤って分類されたデータ点の添字集合を$T_e$と表します。$y_iC_m(x_i)$の値は, $C_m$が$x_i$を正しく分類できていれば$1$, 誤分類していれば$-1$となることに注意すると, 以下のように計算できます。
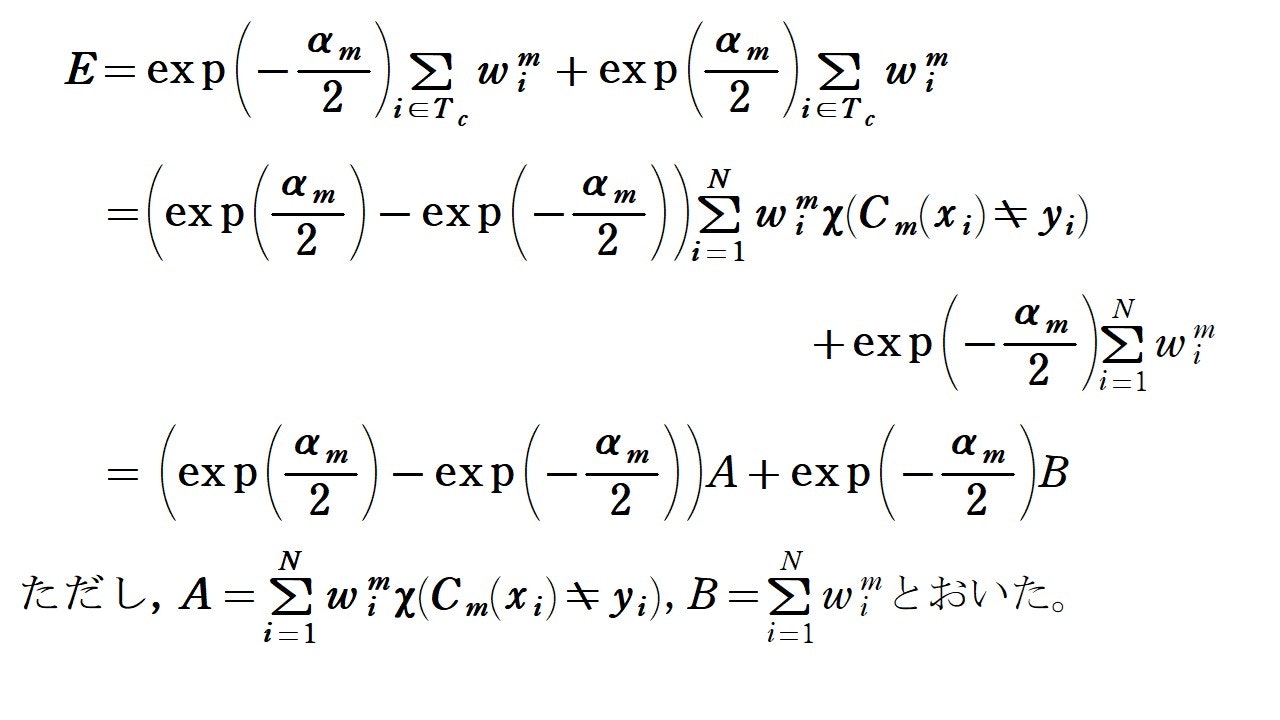
上の計算結果から, $y_m(x)$に関する$E$の最小化は, $B$が定数であることに注意すれば, ①の最小化と同値ということが分かります。なので, 後は$\alpha _m$に関する$E$の最小化を考えればOKです。ということで, $E$を$\alpha _m$で偏微分していきましょう。
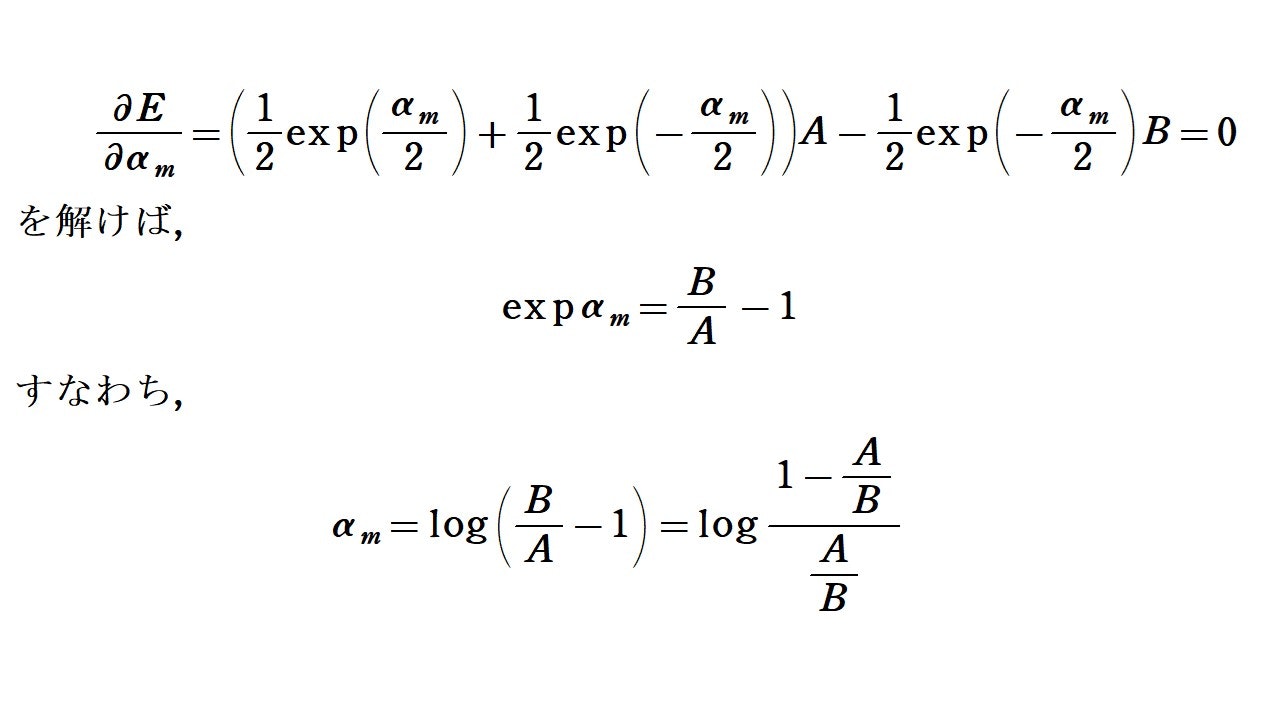
$\frac{A}{B}=E_m$ということに注意すれば, ①と②が得られました。
最後に, 重みの更新についてお話しします。⑤の計算式から各$x_i$と対応する重みの更新は,
$$w_i^{m+1}=w_i^m\exp (-\frac{1}{2}y_i\alpha _mC_m(x_i))$$
で行われることが分かります。この式の$y_iC_m(x_i)$の部分は,
$$y_iC_m(x_i) = 1-2\chi (C_m(x_i)\neq y_i)$$
と表すことができますので, 結局重みの更新式は
$$w_i^{m+1}=w_i^m\exp(-\frac{m}{2})\exp(\alpha _m \chi (C_m(x_i)\neq y_i))$$
となります。③と比較すると$\exp(-\frac{m}{2})$という余計な式が出ているように見えます。しかし, この項は式①で正規化をすると, 約分されて消えてしまいます。ですから, 重みの更新式③を導出することもできました。
長くなりましたが, 以上でアダブーストに関するお話しが完了です。
最後まで読んでいただき誠にありがとうございました。
参考文献
Sebastian Raschka/Vahid Mirjalili著「Python機械学習プログラミング~達人データサイエンティストによる理論と実践~」
平井有三 著「はじめてのパターン認識」