Delphi で２地点間の距離と方位角を求める

はじめに

keisan.casio.jp に２地点間の距離と方位角を求める記事がありまして、

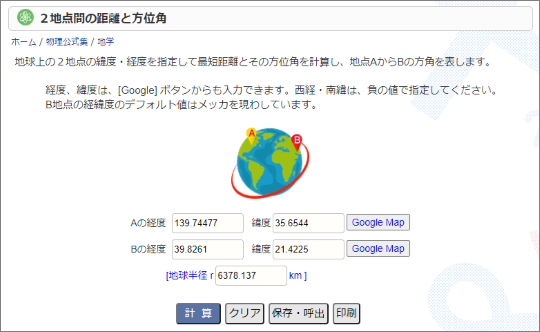
これを Delphi で書いてみようという趣旨となります。

• ２地点間の距離と方位角 (keisan.casio.jp)

なお、地球を楕円体として正確に計算するアルゴリズムは国土地理院のサイトに掲載されていますので、興味のある方はそちらも参照してみてください。

See also:

• 距離と方位角の計算 (国土地理院)

コード

Delphi の持つ数値計算ルーチン

数値計算ルーチンは割と豊富に揃っていますので、アルゴリズムの記述に困る事はないと思います。

• 数値計算ルーチン (DocWiki)

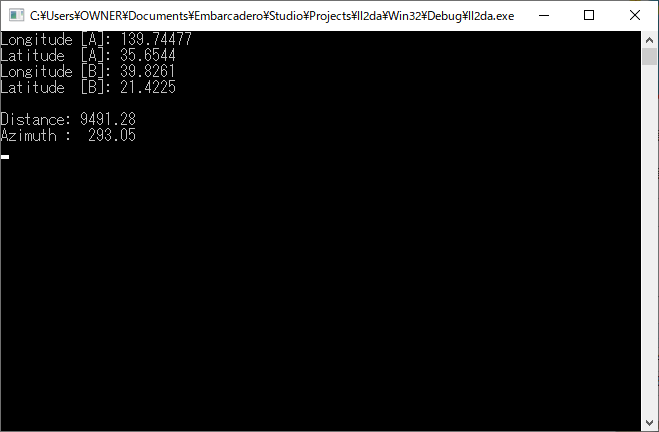
Delphi で書いてみたコード

先のサイトにある計算式をコードにしてみるとこんな感じでしょうか？

ll2da.dpr

program ll2da;
{$APPTYPE CONSOLE}
uses
  System.Math;

const
  r = 6378.137;
var
  x1, y1, x2, y2: Double;
begin
  Write('Longitude [A]: '); Readln(x1); x1 := DegToRad(x1);
  Write('Latitude  [A]: '); Readln(y1); y1 := DegToRad(y1);
  Write('Longitude [B]: '); Readln(x2); x2 := DegToRad(x2);
  Write('Latitude  [B]: '); Readln(y2); y2 := DegToRad(y2);
  Writeln;
  var dx := x2 - x1;
  var dst := r * ArcCos(Sin(y1) * Sin(y2) + Cos(y1) * Cos(y2) * Cos(dx));
  var phi := FMod(360 + 90 - RadToDeg(ArcTan2(Cos(y1) * Tan(y2) - Sin(y1) * Cos(dx), Sin(dx))), 360);
  Writeln('Distance:', dst:10:2);
  Writeln('Azimuth :', phi:10:2);
end.

XE8 以降には実数の剰余を求める事ができる FMod() なんていう関数があります ¹。FMod() を使わず、従来の数値計算ルーチンだけで記述すると次のようになるかと思います。

  var phi := 360 + 90 - RadToDeg(ArcTan2(Cos(y1) * Tan(y2) - Sin(y1) * Cos(dx), Sin(dx)));
  phi := Trunc(phi) mod 360 + Frac(phi);

剰余を求める部分は次のようにも書けるのですが、

  phi := phi - Trunc(phi / 360) * 360;

実数除算する事に (なんとなく) 抵抗があり、先のコードのように整数部と小数部を分けて計算する方が個人的には好きです。

See also:

• System.Math.FMod (DocWiki)

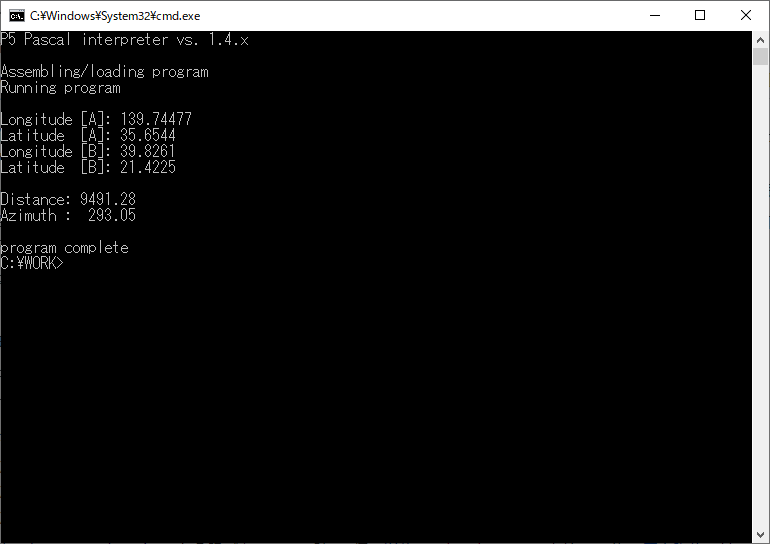
標準 Pascal で書いてみたコード

標準 Pascal の算術関数には Tan() も ArcCos() もないけど、Pascal 50 周年だから書いてみるしかないね！(？)

ll2da.pas

program ll2da(Input, Output);

const
  Pi = 3.1415926535;
  r = 6378.137;
var
  x1, y1, x2, y2, dx, dst, phi: Real;
  function ArcTan2(Y, X: Real): Real; Forward;
  function ArcCos(X: Real): Real;
  begin
    ArcCos := ArcTan2(Sqrt((1 + X) * (1 - X)), X);
  end; { ArcCos }
  function ArcTan2;
  var
    v: Real; 
  begin
    if X = 0 then
      begin
        if Y > 0 then
          ArcTan2 :=  Pi / 2
        else if Y < 0 then
          ArcTan2 := -Pi / 2
        else 
          ArcTan2 := 0;
      end  
    else 
      begin
        v := ArcTan(Y / X);
        if X > 0 then
          ArcTan2 := v
        else  
          begin
            if Y < 0 then
              ArcTan2 := v - Pi
            else  
              ArcTan2 := v + Pi;
          end;
      end;  
  end; { ArcTan2 }
  function DegToRad(Degrees: Real): Real;
  begin
    DegToRad := Degrees * Pi / 180;
  end; { DegToRad }
  function Frac(X: Real): Real;
  begin
    Frac := X - Trunc(X);
  end; { Frac }
  function RadToDeg(Radians: Real): Real;
  begin
    RadToDeg := Radians * 180 / Pi;
  end; { RadToDeg }
  function Tan(X: Real): Real;
  begin
    Tan := Sin(X) / Cos(X);
  end; { Tan } 
begin
  Write('Longitude [A]: '); Readln(x1); x1 := DegToRad(x1);
  Write('Latitude  [A]: '); Readln(y1); y1 := DegToRad(y1);
  Write('Longitude [B]: '); Readln(x2); x2 := DegToRad(x2);
  Write('Latitude  [B]: '); Readln(y2); y2 := DegToRad(y2);
  Writeln;
  dx := x2 - x1;
  dst := r * ArcCos(Sin(y1) * Sin(y2) + Cos(y1) * Cos(y2) * Cos(dx));
  phi := 360 + 90 - RadToDeg(ArcTan2(Cos(y1) * Tan(y2) - Sin(y1) * Cos(dx), Sin(dx)));
  phi := Trunc(phi) mod 360 + Frac(phi);
  Writeln('Distance:', dst:10:2);
  Writeln('Azimuth :', phi:10:2);
end.

ちょっと長くなりましたね。コードの 4 割位を ArcTan2() ² 関数が占めています (w

おわりに

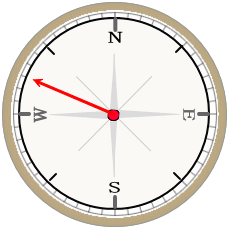
参考にしたサイトの入力ボックスにデフォルトで設定されている２地点は東京とメッカなのですが、

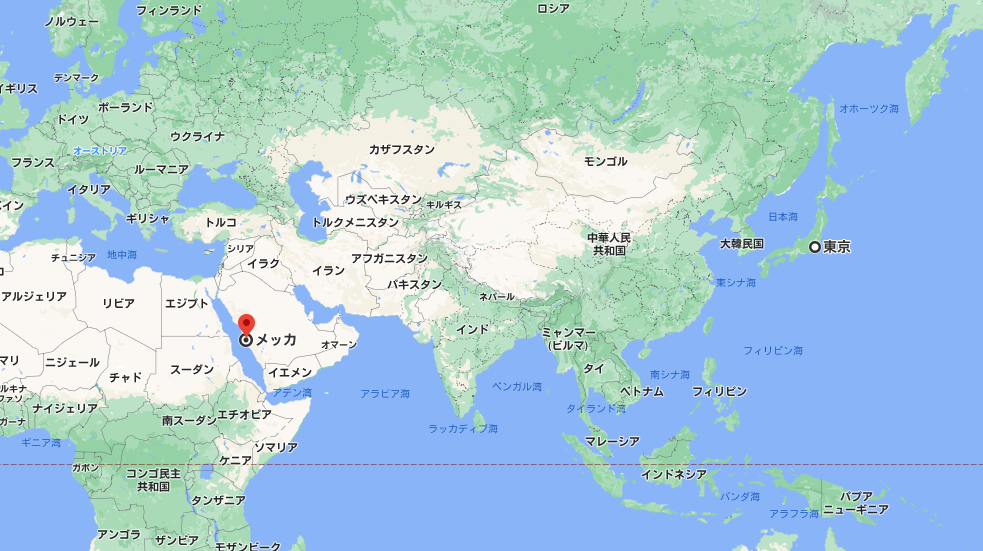
方位角は、世界地図を見た時の直感とは異なる方向を指していますよね。

1. System.Math には他にも見慣れない関数が...いつの間に？ ↩

2. ArcTan2() がアルゴリズム的にこれでいいのかは要検証。Delphi の System.Math にある ArcTan2() はルックアップテーブルを使って値を求めている。恐らくこちらの方が高速に動作するアルゴリズムなのだろう。 ↩