Delphi と複素数

はじめに

先日、標準 Pascal と数 という記事を書きました。自然数 / 整数 / 有理数 / 実数に関するものだったのですが、複素数については触れていませんでした。

複素数

複素数そのものについては数学の話になるので、軽く触れるだけにしておきます。

一般

加算	減算	乗算	除算
〇	〇	〇	〇

• 2 つの実数 a, b と虚数単位 i を使って z = a + bi と表せる数
• b=0 なら実数、b≠0 なら虚数 (さらに a=0 なら純虚数)
• 記号は ℂ
• つまり ℕ⊂ℤ⊂ℚ⊂ℝ⊂ℂ
• 複素数同士の四則演算はすべて完全に可能
• コンピュータでは様々な方法で実装されている

Pascal

• 標準 Pascal には複素数をサポートする機能がありません
• 『コンピュータアルゴリズム辞典』には複素数を計算するアルゴリズムが掲載されています

C 言語ですと ISO/IEC 9899:1999 (C99) にて複素数計算に必要なデータ型や関数の定義が追加されています。

See also:

• 複素数 (Wikipedia)

Delphi と複素数

2001 年発売の Delphi 6 以降、RTL に複素数計算のための VarCmplx というユニットが追加されています。

Delphi での複素数型は カスタム Variant で実装されています。実態はクラスなのですが、ただの Variant 型のように使う事ができます。

カスタム Variant

カスタム Variant を作るには、TCustomVariantType クラスを継承して、新しい Variant 型をインスタンス化します。RTL には複素数のカスタム Variant の他に、ConvUtils に含まれる度量衡計算のためのカスタム Variant があります。

See also:

• System.Variants.TCustomVariantType (DocWiki)
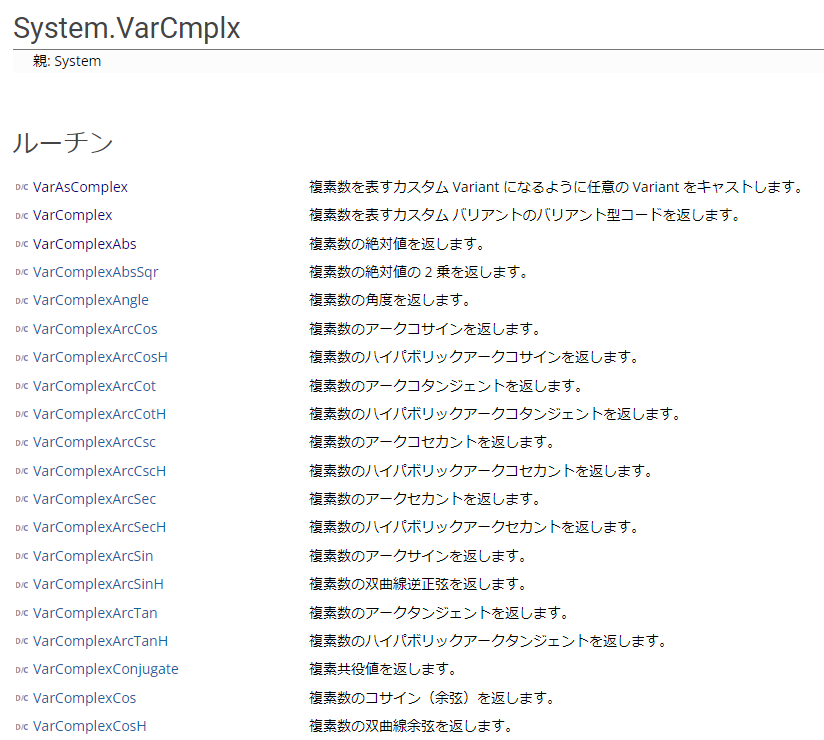
• System.VarCmplx (DocWiki)
• System.ConvUtils (DocWiki)
• 度量衡計算を行うには？ (Delphi 6 以降) (ht-deko.com)

複素数型カスタム Variant の使い方

複素数型カスタム Variant を使うには、VarComplexCreate() を用います。

CmplxTest.dpr

program CmplxTest;
{$APPTYPE CONSOLE}
uses
  System.SysUtils, System.VarCmplx;
var
  a, b: Double;
  z: Variant;
begin
  a := 2;
  b := 3;
  z := VarComplexCreate(a, b); // z = 2 + 3i;
  Writeln(z);                  // Text: 2 + 3i
end.

オーバーロードされた関数を使えば、文字列から複素数型カスタム Variant を生成できます。

CmplxTest2.dpr

program CmplxTest2;
{$APPTYPE CONSOLE}
uses
  System.SysUtils, System.VarCmplx;
var
  z: Variant;
begin
  z := VarComplexCreate('2 + 3i'); // z = 2 + 3i;
  Writeln(z);                      // Text: 2 + 3i
end.

プロパティを使って実部と虚部を取り出す事もできます。

CmplxTest3.dpr

program CmplxTest3;
{$APPTYPE CONSOLE}
uses
  System.SysUtils, System.VarCmplx;
var
  z: Variant;
  a, b: Double;
begin
  z := VarComplexCreate('2 + 3i'); // z = 2 + 3i;
  a := z.Real;                     // z の実部
  b := z.Imaginary;                // z の虚部
  Writeln(a:8:2);                  // a = 2.00
  Writeln(b:8:2);                  // b = 3.00
end.

プロパティ	説明	ルーチン
Real	複素数の実部
Imaginary	複素数の虚部
Radius	複素数平面上の絶対値 (半径)	VarComplexAbs()
Theta	複素数平面上の偏角	VarComplexAngle()
FixedTheta	複素数平面上の偏角 (-π..π)

演算子のオーバーロードがあるため、複素数型カスタム Variant 同士の四則演算 (及び否定) はそのまま可能です。

CmplxTest4.dpr

program CmplxTest4;
{$APPTYPE CONSOLE}
uses
  System.SysUtils, System.VarCmplx;

begin
  var z := VarComplexCreate('2+3i'); // z = 2+3i
  var y := VarComplexCreate('5-1i'); // y = 5-i
  var x := z * y;                    // x = (2+3i)(5-i)
  Writeln(x);                        // 13 + 13i
end.

その他の計算については専用のルーチンが用意されています。

See also:

• System.VarCmplx.VarComplexCreate (DocWiki)
• System.Math.RadToDeg (DocWiki)
• 複素数の偏角 (Wikipedia)

複素数レコード TComplex

サンプルプログラムフォルダ Object Pascal/RTL には、ComplexNumbers というプロジェクトが含まれています。これは Hallvard Vassbotn 氏による複素数レコード TComplex を使うサンプルプログラムとなっています。

• /Object Pascal/RTL/ComplexNumbers/ - RAD Studio 11 Demos (Github)

サンプルプログラム ComplexNumbers は Delphi 2006 から (?) 含まれています。TComplex は高度なレコード型 (Advanced Record) なので、Delphi 2005 以前の環境では使えません。

TComplex レコードを使うには Vassbotn.Vcl.Complex.pas だけあればよく、uses に Vassbotn.Vcl.Complex を追加して使います。

このユニットは名前に vcl と入っていますが、RTL サンプルフォルダ内ですし、プラットフォームに依存するものは特になさそうです。

また、複素数カスタム Variant を使うよりも TComplex レコードを使った方がパフォーマンスは良いようです。

CmplxTest5.dpr

program CmplxTest5;
{$APPTYPE CONSOLE}
uses
  System.SysUtils, Vassbotn.Vcl.Complex;
var
  z: TComplex;
begin
  z := TComplex.From(2, 3); // z = 2+3i
  Writeln(z.ToString);
end.

サンプルプログラム ComplexNumbers は残念な事に Delphi 12 Athens にて削除されています。Delphi 12 Athens において、浮動小数点例外がデフォルトで無効になっているのが削除の理由だと思われます。

See also:

• RAD Studio 12.0 Athens の新機能 (DocWiki)
• Floating Point Operation Exception Masks (DocWiki: en)

複素数レコード TComplex (その 2)

『コンピュータアルゴリズム辞典』PP.117-121 にあるアルゴリズムを高度なレコード型で実装してみました。四則演算と絶対値、極座標変換が使えます。

uComplex.pas

unit uComplex;

interface

uses
  System.SysUtils, System.Math;

type
  TComplex = record
  private
    FImaginary: Double;
    FReal: Double;
    procedure ConvertToPolar(c: TComplex; var R, Th: Double);
    function GetFixedTheta: Double;
    function GetRadius: Double;
    function GetTheta: Double;
    procedure SetImaginary(const Value: Double);
    procedure SetReal(const Value: Double);
  public
    constructor Create(r, i: Double);
    class operator Add(a, b: TComplex): TComplex;                  // +
    class operator Divide(a, b: TComplex): TComplex;               // /
    class operator Equal(a, b: TComplex): Boolean;                 // =
    class operator Multiply(a, b: TComplex): TComplex;             // *
    class operator NotEqual(a, b: TComplex): Boolean;              // <>
    class operator Subtract(a, b: TComplex): TComplex;             // -
    procedure ToPolar(var R, Th: Double);
    function ToString: string; overload;
    property FixedTheta: Double read GetFixedTheta;                // 偏角 (-π..π)
    property Imaginary: Double read FImaginary write SetImaginary; // 虚部
    property Radius: Double read GetRadius;                        // 絶対値
    property Real: Double read FReal write SetReal;                // 実部
    property Theta: Double read GetTheta;                          // 偏角
  end;

implementation

{ TComplex }

class operator TComplex.Add(a, b: TComplex): TComplex;
begin
  result.Real := a.Real + b.Real;
  result.Imaginary := a.Imaginary + b.Imaginary;
end;

procedure TComplex.ConvertToPolar(c: TComplex; var R, Th: Double);
var
  T: Double;
begin
  if c.Real < 0 then
  begin
    if c.Imaginary >= 0 then
      Th := Pi
    else
      Th := - Pi;
    c.Real := - c.Real;
    c.Imaginary := - c.Imaginary
  end
  else
    Th := 0;
  if c.Imaginary > c.Real then
  begin
    T := c.Real;
    c.Real := c.Imaginary;
    c.Imaginary := - T;
    Th := Th + Pi / 2
  end
  else if c.Imaginary < - c.Real then
  begin
    T := c.Real;
    c.Real := - c.Imaginary;
    c.Imaginary := T;
    Th := Th - Pi / 2
  end;
  if c.Real > 0 then
  begin
    R := Sqrt(Sqr(c.Imaginary / c.Real) + 1) * c.Real;
    Th := ArcTan(c.Imaginary / c.Real) + Th
  end
  else
  begin
    R := 0;
    Th := 0 (* 本当は Th は不定 *)
  end
end;

constructor TComplex.Create(r, i: Double);
begin
  FReal := r;
  FImaginary := i;
end;

class operator TComplex.Divide(a, b: TComplex): TComplex;
var
  T, U: Double;
begin
  if (b.Real = 0) and (b.Imaginary = 0) then
    raise EDivByZero.Create('０では割れません')
  else if Abs(b.Real) >= Abs(b.Imaginary) then
  begin
    T := b.Imaginary / b.Real;
    U := b.Real + b.Imaginary * T;
    Result.Real := (a.Real + a.Imaginary * T) / U;
    Result.Imaginary := (a.Imaginary - a.Real * T) / U
  end
  else
  begin
    T := b.Real / b.Imaginary;
    U := b.Real * T + b.Imaginary;
    Result.Real := (a.Real * T + a.Imaginary) / U;
    Result.Imaginary := (a.Imaginary * T - a.Real) / U
  end
end;

class operator TComplex.Equal(a, b: TComplex): Boolean;
begin
  Result := SameValue(a.Real, b.Real) and
            SameValue(a.Imaginary, b.Imaginary);
end;

function TComplex.GetFixedTheta: Double;
begin
  Result := System.Math.ArcTan2(Self.Imaginary, Self.Real);
end;

function TComplex.GetRadius: Double;
begin
  if Self.Real = 0 then
    Result := Abs(Self.Imaginary)
  else if Self.Imaginary = 0 then
    Result := Abs(Self.Real)
  else if Abs(Self.Imaginary) > Abs(Self.Real) then
    Result := Abs(Self.Imaginary) * Sqrt(1 + Sqr(Self.Real / Self.Imaginary))
  else
    Result := Abs(Self.Real) * Sqrt(1 + Sqr(Self.Imaginary / Self.Real))
end;

function TComplex.GetTheta: Double;
begin
  Result := System.ArcTan(Self.Imaginary / Self.Real);
end;

class operator TComplex.Multiply(a, b: TComplex): TComplex;
begin
  Result.Real := a.Real * b.Real - a.Imaginary * b.Imaginary;
  Result.Imaginary := a.Real * b.Imaginary + a.Imaginary * b.Real;
end;

class operator TComplex.NotEqual(a, b: TComplex): Boolean;
begin
  Result := not (a = b);
end;

procedure TComplex.SetImaginary(const Value: Double);
begin
  FImaginary := Value;
end;

procedure TComplex.SetReal(const Value: Double);
begin
  FReal := Value;
end;

class operator TComplex.Subtract(a, b: TComplex): TComplex;
begin
  result.Real := a.Real - b.Real;
  result.Imaginary := a.Imaginary - b.Imaginary;
end;

procedure TComplex.ToPolar(var R, Th: Double);
begin
  ConvertToPolar(Self, R, Th);
end;

function TComplex.ToString: string;
const
  SignChar: array [Boolean] of Char = ('-', '+');
var
  RStr, IStr: string;
begin
  RStr := FloatToStr(Self.Real);
  IStr := FloatToStr(System.Abs(Self.Imaginary));
  Result := Format('%s %s %s%s', [RStr, SignChar[Self.Imaginary >= 0], IStr, 'i']);
end;
end.

次のような使い方になります。

CmplxTest6.dpr

program CmplxTest6;
{$APPTYPE CONSOLE}
uses
  System.SysUtils, uComplex;

begin
  var z := TComplex.Create(-1, 6); // z = -1 + 6i;
  var y := TComplex.Create(4, -3); // y = 4 - 3i;
  var x := z * y;
  Writeln(x.ToString);             // x = 14 + 27i
  Writeln(x.Real:8:2);
  Writeln(x.Imaginary:8:2);
end.

実行結果は次のようになります。

14 + 27i
   14.00
   27.00

See also:

• 『コンピュータ・アルゴリズム事典』サポートページ

複素数レコード TComplex (その 3)

『コンピュータアルゴリズム辞典』には改訂版とも言うべき『C 言語による最新アルゴリズム辞典』があります。こちらには複素数関係のアルゴリズムが複素数ライブラリ (complex.c) という形で収録されています。

折角なので、このライブラリを Delphi に移植してみる事にしました。高度なレコード型を使っているので、メソッド名は Delphi が持つ数値計算ルーチンに準拠させてあります。オリジナルは c_sin() のようなルーチンですが、TComplex.Sin() のようにして使う事ができます。

uComplex.pas

unit uComplex;
// https://github.com/okumuralab/algo-c/blob/main/src/complex.c

interface

uses
  System.SysUtils, System.Math;

type
  TComplex = record
  private
    FImaginary: Double;
    FReal: Double;
    procedure ConvertToPolar(c: TComplex; var R, Th: Double);
    function GetFixedTheta: Double;
    function GetRadius: Double;
    function GetTheta: Double;
    procedure SetImaginary(const Value: Double);
    procedure SetReal(const Value: Double);
  public
    constructor Create(r, i: Double);
    class operator Add(a, b: TComplex): TComplex;                  // +
    class operator Divide(a, b: TComplex): TComplex;               // /
    class operator Equal(a, b: TComplex): Boolean;                 // =
    class operator Multiply(a, b: TComplex): TComplex;             // *
    class operator NotEqual(a, b: TComplex): Boolean;              // <>
    class operator Subtract(a, b: TComplex): TComplex;             // -
    class function Abs(const c: TComplex): Double; static;         // 絶対値
    class function Conjugate(const c: TComplex): TComplex; static; // 共役複素数
    class function Cos(const c: TComplex): TComplex; static;       // Cos: 余弦
    class function Cosh(const c: TComplex): TComplex; static;      // Cosh: 双曲線余弦
    class function Exp(const c: TComplex): TComplex; static;       // Exp: 指数関数
    class function Ln(const c: TComplex): TComplex; static;        // Ln: 自然対数
    class function Power(const x, y: TComplex): TComplex; static;  // Power: 累乗
    class function Sin(const c: TComplex): TComplex; static;       // Sin: 正弦
    class function Sinh(const c: TComplex): TComplex; static;      // Sinh: 双曲線正弦
    class function Sqrt(const c: TComplex): TComplex; static;      // Sqrt: 平方根
    class function Tan(const c: TComplex): TComplex; static;       // Tan: 正接
    class function Tanh(const c: TComplex): TComplex; static;      // Tanh: 双曲線正接
    procedure ToPolar(var R, Th: Double);
    function ToString: string; overload;
    property FixedTheta: Double read GetFixedTheta;                // 偏角 (-π..π)
    property Imaginary: Double read FImaginary write SetImaginary; // 虚部
    property Radius: Double read GetRadius;                        // 絶対値
    property Real: Double read FReal write SetReal;                // 実部
    property Theta: Double read GetTheta;                          // 偏角
  end;

implementation

{ TComplex }

class function TComplex.Abs(const c: TComplex): Double;
begin
  if c.Real = 0 then
    Result := System.Abs(c.Imaginary)
  else if c.Imaginary = 0 then
    Result := System.Abs(c.Real)
  else if System.Abs(c.Imaginary) > System.Abs(c.Real) then
    Result := System.Abs(c.Imaginary) * System.Sqrt(1 + System.Sqr(c.Real / c.Imaginary))
  else
    Result := System.Abs(c.Real) * System.Sqrt(1 + System.Sqr(c.Imaginary / c.Real))
end;

class operator TComplex.Add(a, b: TComplex): TComplex;
begin
  Result.Real      := a.Real + b.Real;
  Result.Imaginary := a.Imaginary + b.Imaginary;
end;

class function TComplex.Conjugate(const c: TComplex): TComplex;
begin
  Result.Imaginary := - c.Imaginary;
end;

procedure TComplex.ConvertToPolar(c: TComplex; var R, Th: Double);
var
  T: Double;
begin
  if c.Real < 0 then
  begin
    if c.Imaginary >= 0 then
      Th := Pi
    else
      Th := - Pi;
    c.Real := - c.Real;
    c.Imaginary := - c.Imaginary
  end
  else
    Th := 0;
  if c.Imaginary > c.Real then
  begin
    T := c.Real;
    c.Real := c.Imaginary;
    c.Imaginary := - T;
    Th := Th + Pi / 2
  end
  else
  if c.Imaginary < - c.Real then
  begin
    T := c.Real;
    c.Real := - c.Imaginary;
    c.Imaginary := T;
    Th := Th - Pi / 2
  end;
  if c.Real > 0 then
  begin
    R := System.Sqrt(System.Sqr(c.Imaginary / c.Real) + 1) * c.Real;
    Th := System.ArcTan(c.Imaginary / c.Real) + Th
  end
  else
  begin
    R := 0;
    Th := 0 (* 本当は Th は不定 *)
  end
end;

class function TComplex.Cos(const c: TComplex): TComplex;
var
  e, f: Double;
begin
  e := System.Exp(c.Imaginary);
  f := 1 / e;
  Result.Imaginary := 0.5 * System.Sin(c.Real) * (f - e);
  Result.Real      := 0.5 * System.Cos(c.Real) * (f + e);
end;

class function TComplex.Cosh(const c: TComplex): TComplex;
var
  e, f: Double;
begin
  e := System.Exp(c.Real);
  f := 1 / e;
  Result.Real      := 0.5 * (e + f) * System.Cos(c.Imaginary);
  Result.Imaginary := 0.5 * (e - f) * System.Sin(c.Imaginary);
end;

constructor TComplex.Create(r, i: Double);
begin
  FReal      := r;
  FImaginary := i;
end;

class operator TComplex.Divide(a, b: TComplex): TComplex;
var
  T, U: Double;
begin
  if System.Abs(b.Real) >= System.Abs(b.Imaginary) then
  begin
    T := b.Imaginary / b.Real;
    U := b.Real + b.Imaginary * T;
    Result.Real      := (a.Real + a.Imaginary * T) / U;
    Result.Imaginary := (a.Imaginary - a.Real * T) / U
  end
  else
  begin
    T := b.Real / b.Imaginary;
    U := b.Real * T + b.Imaginary;
    Result.Real      := (a.Real * T + a.Imaginary) / U;
    Result.Imaginary := (a.Imaginary * T - a.Real) / U
  end
end;

class operator TComplex.Equal(a, b: TComplex): Boolean;
begin
  Result := SameValue(a.Real, b.Real) and
            SameValue(a.Imaginary, b.Imaginary);
end;

class function TComplex.Exp(const c: TComplex): TComplex;
var
  a: Double;
begin
  a := System.Exp(c.Real);
  Result.Real      := a * System.Cos(c.Imaginary);
  Result.Imaginary := System.Sin(c.Imaginary);
end;

function TComplex.GetFixedTheta: Double;
begin
  Result := System.Math.ArcTan2(Self.Imaginary, Self.Real);
end;

function TComplex.GetRadius: Double;
begin
  Result := TComplex.Abs(Self);
end;

function TComplex.GetTheta: Double;
begin
  Result := System.ArcTan(Self.Imaginary / Self.Real);
end;

class function TComplex.Ln(const c: TComplex): TComplex;
begin
  Result.Real      := 0.5 * System.Ln(c.Real * c.Real + c.Imaginary * c.Imaginary);
  Result.Imaginary := System.Math.ArcTan2(c.Imaginary, c.Real);
end;

class operator TComplex.Multiply(a, b: TComplex): TComplex;
begin
  Result.Real      := a.Real * b.Real - a.Imaginary * b.Imaginary;
  Result.Imaginary := a.Real * b.Imaginary + a.Imaginary * b.Real;
end;

class operator TComplex.NotEqual(a, b: TComplex): Boolean;
begin
  Result := not (a = b);
end;

class function TComplex.Power(const x, y: TComplex): TComplex;
begin
  Result := TComplex.Exp(y * TComplex.Ln(x));
end;

procedure TComplex.SetImaginary(const Value: Double);
begin
  FImaginary := Value;
end;

procedure TComplex.SetReal(const Value: Double);
begin
  FReal := Value;
end;

class function TComplex.Sin(const c: TComplex): TComplex;
var
  e, f: Double;
begin
  e := System.Exp(c.Imaginary);
  f := 1 / e;
  Result.Imaginary := 0.5 * System.Cos(c.Real) * (e - f);
  Result.Real      := 0.5 * System.Sin(c.Real) * (e + f);
end;

class function TComplex.Sinh(const c: TComplex): TComplex;
var
  e, f: Double;
begin
  e := System.Exp(c.Real);
  f := 1 / e;
  Result.Real      := 0.5 * (e - f) * System.Cos(c.Imaginary);
  Result.Imaginary := 0.5 * (e + f) * System.Sin(c.Imaginary);
end;

class function TComplex.Sqrt(const c: TComplex): TComplex;
const
  SQRT05 = 0.707106781186547524;
var
  r, w: Double;
begin
  r := TComplex.Abs(c);
  w := System.Sqrt(r + System.Abs(c.Real));
  if c.real >= 0 then
  begin
    Result.Real      := SQRT05 * w;
    Result.Imaginary := SQRT05 * c.Imaginary / w;
  end
  else
  begin
    Result.Real      := SQRT05 * System.Abs(c.Imaginary) / w;
    if c.Imaginary >= 0 then
      Result.Imaginary :=  SQRT05 * w
    else
      Result.Imaginary := -SQRT05 * w;
  end;
end;

class operator TComplex.Subtract(a, b: TComplex): TComplex;
begin
  Result.Real      := a.Real - b.Real;
  Result.Imaginary := a.Imaginary - b.Imaginary;
end;

class function TComplex.Tan(const c: TComplex): TComplex;
var
  e, f, d: Double;
begin
  e := System.Exp(2 * c.Imaginary);
  f := 1 / e;
  d := System.Cos(2 * c.Real) + 0.5 * (e + f);
  Result.Real      := System.Sin(2 * c.Real) / d;
  Result.Imaginary := 0.5 * (e - f) / d;
end;

class function TComplex.Tanh(const c: TComplex): TComplex;
var
  e, f, d: Double;
begin
  e := System.Exp(2 * c.Real);
  f := 1 / e;
  d := 0.5 * (e + f) * System.Cos(2 * c.Imaginary);
  Result.Real      := 0.5 * (e - f) / d;
  Result.Imaginary := System.Sin(2 * c.Imaginary) / d;
end;

procedure TComplex.ToPolar(var R, Th: Double);
begin
  ConvertToPolar(Self, R, Th);
end;

function TComplex.ToString: string;
const
  SignChar: array [Boolean] of Char = ('-', '+');
var
  RStr, IStr: string;
begin
  RStr := FloatToStr(Self.Real);
  IStr := FloatToStr(System.Abs(Self.Imaginary));
  Result := Format('%s %s %s%s', [RStr, SignChar[Self.Imaginary >= 0], IStr, 'i']);
end;
end.

See also:

• C言語による最新アルゴリズム事典 (技術評論社)
• C言語による最新アルゴリズム事典 サポートページ
• ［改訂新版］C言語による標準アルゴリズム事典 (技術評論社)
• ［改訂新版］C言語による標準アルゴリズム事典 サポートページ

おわりに

Delphi で複素数の計算を行う方法についてでした。

Vassbotn.Vcl.Complex の TComplex レコードを Delphi 12 Athens で試したみたのですが、軽く触った程度では問題は発生しませんでした。