Section1 勾配消失問題
誤差逆伝播法で下位層に進んでいくにつれて
勾配がどんどん緩やかになっていく
そのため、勾配降下法による、更新では下位層のパラメータは
ほとんど変わらず訓練は最適地に収束しなくなる
活性化関数
シグモイド関数
大きな値では出力が微小なため、勾配消失問題を引き起こす可能性がある
シグモイド関数の微分の最大値は0.25でありこれをかけていくことになるので勾配が0に近いていくことがわかる
ReLU
勾配消失問題の回避に関してよい成果をもたらしている
ある閾値を超えたらそのままの値を返す関数なので勾配消失が起きにくい
スパース化という観点でもメリットがある
精度の面でも担保されている
初期値の設定方法
Xavierの初期値を設定する際の活性化関数
- relu
- シグモイド
- 双曲線正接関数
重みの要素を前の層のノード数の平方根で除算した値
self.params['W1'] = np.random.randn(input_size, hidden_size) / nq.sqrt(input_layer_size)
self.params['W2'] = np.random.randn(hidden_size, output_size) / nq.sqrt(hidden_layer_size)
Heの初期値を設定する際の活性化関数
- Relu
重みの要素を前の層のノード数の平方根で除算した値に対して$\sqrt2$を掛け合わせたもの
self.params['W1'] = np.random.randn(input_size, hidden_size) / nq.sqrt(input_layer_size)*np.sqrt(2)
self.params['W2'] = np.random.randn(hidden_size, output_size) / nq.sqrt(hidden_layer_size)*np.sqrt(2)
バッチ正規化
ミニバッチ単位で、入力値のデータの偏りを抑制する手法
活性化関数に値を渡す前後に、バッチ正規化の処理を孕んだ層を加える
Section2 学習率最適化手法
初期の学習率の設定方法の方針
-
初期の学習率を大きく設定し徐々に学習率を小さくしていく
-
パラメータごとに学習率を可変させる
-
学習率最適化手法を使用して学習率を最適化
モメンタム
誤差をパラメータで微分したものを学習率の積を減算した後、現在の重みを前回の重みに減算した値と感性の積を加算する
数式
$$
V_t = \mu V_{t-1}-\epsilon \Delta E
$$
$$
W^{(t+1)}=w^{(t)}+V_t
$$
$$\text{慣性:}\mu$$
メリット
- 局所的最適解にならず、大域的最適解となる
- 谷間についてから最も低い位置に行くまで時間が早い
AdaGrad
誤差をパラメータで微分したものと再定義した学習率の席を減算する
数式
h_o = \theta \\
h_t = h_(t-1) + (\Delta E)^2 \\
w^(t+1)=w^(t)-\epsilon \frac{1}{\sqrt{h_t}+\theta}\Delta E
メリット
- 勾配の緩やかな斜面に対して最適値に近づける
デメリット
- 学習率が徐々に小さくなるので鞍点問題を引き起こすことがあった
RMSProp
誤差をパラメータで微分したものと再定義した学習率の席を減算する
AdaGrad のデメリット解消する
数式
h_o = \theta \\
h_t = ah_(t-1) + (1-a)(\Delta E)^2 \\
w^(t+1)=w^(t)-\epsilon \frac{1}{\sqrt{h_t}+\theta}\Delta E
メリット
- 局所的最適解にはならず、大域的最適解となる。
- ハイパーパラメータの調整が必要な場合が少ない
Adam
モメンタムの過去の勾配の指数関数的減衰移動平均
RMSPropの過去の勾配の二乗の指数関数的減衰移動平均
上記二つの孕んだ最適化アルゴリズム
メリット
モメンタムとRMSPropのメリットを孕んだアルゴリズム
Section3
Weight Decay (荷重減衰)
大きいということは、重要な特徴量を表現している可能性があるが、重みが大きすぎるということは、過学習の可能性がある。
誤差(関数)に対して、正則化項を加算することで、重みを抑制する。
L1正則化、L2正則化
正則化とは
ネットワークの自由度に対してルールを加え、一定の方向に制限を行う
数式
En(w)+\frac{1}{pλ}||x||p\\
||x||_p=(|x_1|^p + \dots+|x_n|^p)^{\frac{1}{p}}
p=1 の場合、L1正規化と呼ぶ。
p=2 の場合、L2正規化と呼ぶ。
ドロップアウト
ランダムにノードを削除して学習させること
メリット
データ量を変化せずに異なるモデルを学習させていると解釈できる
Section4
CNN
主に画像に関するモデルを作成することに用いられる。
畳み込み層とプーリング層、全結合層から構成される。
畳み込み層
縦・横・チャンネルの3次元のデータをそのまま学習し、次に伝えることができる
フィルター
全結合でいう重み
バディング
入力画像の辺に入力値を追加することで、画像のサイズを可変すること
ゼロで埋める場合 → ゼロパディングと呼ぶ。( 学習に影響を与えにくい )
ストライド
フィルターで順次抽出する際の、 x および y に対する移動量をストライドという
チャンネル
奥行きの部分。層の数=チャンネル数
例(RGB)
プーリング層
マックスプーリング
畳み込み層の出力を入力とし、そのうちの最大値を出力する。
アベレージプーリング
畳み込み層の出力を入力とし、それらの入力の平均値を出力する。
Section5
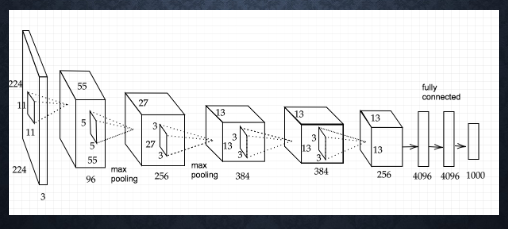
AlexNet
2012年の ILSVRC で優勝
5層の畳み込み層およびプーリング層など、それに続く3層の全結合層から構成される
サイズ4096の全結合層の出力にドロップアウトを使用している
確認テスト
連鎖律の原理を使い、dz/dxを求めよ
$$
z = t^2
$$
$$
t = x + y
$$
解答
$$\frac{dz}{dt}=2t$$
$$\frac{dt}{dx}=1$$
$$\frac{dz}{dx}= \frac{dz}{dt}\frac{dt}{dx}$$
$$\frac{dz}{dx}=2t=2(x + y)$$
シグモイド関数を微分した時、入力値が0の時に最大値をとる。その値 として正しいものを選択肢から選べ。
(1) 0.15
(2) 0.25
(3) 0.35
(4) 0.45
解答
シグモイド関数の微分は以下のようになる
$ (1- sigmoid(x))・sigmoid(x)$
0.5の時最大なので
(1-0.5)・(0.5)=0.25
(2)
重みの初期値に0を設定すると、どのような問題が発生するか。簡潔に説明せよ
解答
全ての値が同じ値で伝わるためパラメータのチューニングが行われなくなる
一般的に考えられるバッチ正規化の効果を2点挙げよ
解答
- 計算時間が短縮される。
- 勾配消失が起きづらくなる。
モメンタム・AdaGrad・RMSPropの特徴をそれぞれ簡潔に説明せよ
解答
モメンタム
- 局所的最適解ではなく、大域的最適解が得られやすい。
AdaGrad
- なだらかな部分でも最適地に収束しやすい
RMSProp
- パラメータの調整が少なくて済む
機械学習で使われる線形モデル(線形回帰、主成分分析・・・etc)の正則化は、モデルの重みを制限することで可能となる。 前述の線形モデルの正則化手法の中にリッジ回帰という手法があり、その特徴として正しいものを選択しなさい。
(a) ハイパーパラメータを大きな値に設定すると、すべての重みが限りなく0に近づく
(b) パイパーパラメータを 0 に設定すると、非線形回帰となる
(c) バイアス項についても、正則化される
(d) リッジ回帰の場合、隠れ層に対して正則化項を加える
解答
(a)
(a) リッジ回帰(L2正則化)
(b) 正則化を行っても、線形回帰が非線形回帰にならない
(c) バイアスに関しては正則化されない
(d) 正則化に関しては誤差関数に対して正則化項を加える
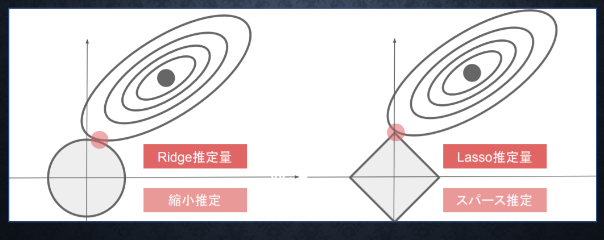
下図について、L1正則化を表しているグラフはどちらか答えよ。
解答
左側 L2 正則化
右側 L1正則化
サイズ6×6の入力画像を、サイズ2×2のフィルタで畳み込んだ時の出力画像のサイズを答えよ。なおストライドとパディングは1とする。
解答
7×7
実践演習
勾配消失問題の解決実装
結果
https://github.com/Tomo-Horiuchi/rabbit/blob/master/part2/2Day/2_2_1_vanishing_gradient.ipynb
https://github.com/Tomo-Horiuchi/rabbit/blob/master/part2/2Day/2_4_optimizer.ipynb
https://github.com/Tomo-Horiuchi/rabbit/blob/master/part2/2Day/2_5_overfiting.ipynb
https://github.com/Tomo-Horiuchi/rabbit/blob/master/part2/2Day/2_6_simple_convolution_network.ipynb
考察
活性化関数をシグモイドからReLUに変える変えることで勾配消失問題の改善が見られた
重みの初期化についてはXavierではreluとシグモイド両方で勾配消失問題の改善が見られた
Heの場合はReLUのみ勾配消失の改善が見られた
今回の結果より勾配消失問題は重みの初期値や活性化関数の調節で改善できることが分かった
学習率によって学習する速度や精度が変化することが分かった
学習率最適化手法を使用する事によって学習が進むようになったりした。
正則化の強度が大きいと精度があがらない 小さいと過学習が抑えられない
ドロップアウトによって過学習が抑えられていることがわかる
im2colによって画像を二次元配列になるということを確認できた
im2colとim2colの整合性はない
CNNを利用することにより画像データの学習が進められることが確認できた
畳み込みの計算などPCのスペックが必要であるということを感じた