GDSC Japan Advent Calender 2023 11日目をGDSC UTからお届けします。
これはなに
機械学習の研究✨をやっているので「なんか研究の話して」って振られ、ネタに困っていたところに
(なんか近い論文を最近読んだし乗るしかない!)ということで[Lebedev et al. ICLR 2015.]の紹介です!
実装→NVIDIAの強い研究者のGitHubにあるJupyterNotebook
この記事の主題
「GPUで訓練した深層学習モデルをCPU上で動かしてアプリケーションに組み込みたい......」
「高精度で画像認識できる巨大な事前学習済み畳み込みニューラルネットワーク(CNN)を、一体どうすれば精度を落とさずに軽量化できるか?」
といった問いに対し、シンプルな線形代数の延長にある手法で答えます💪
興味を持ってもらえると幸いです!
畳み込み層の定式化
4x4の画像(青)を、3x3のカーネルを使用して畳み込むと、2x2の出力(緑)を得ます。
カーネル幅が3x3だと、入力の画像が縦横に2ずつ小さくなりますね。
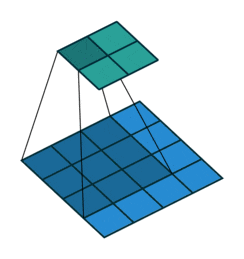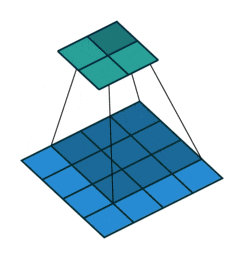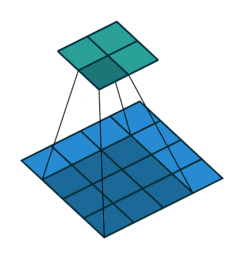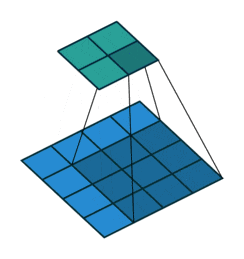
https://github.com/vdumoulin/conv_arithmetic/blob/master/gif/no_padding_no_strides.gif
だだし現実の状況では、画像の各ピクセルはRGBの3チャネルあるので、
256x256x3の画像(青)を、3x3x3のカーネルを使用して畳み込み、254x254の出力(緑)を得ます。
T個のカーネルを使うと出力はTチャネルでサイズは254x254xTになり、これを次の畳み込み層に入力すると254x254xTの画像が......を繰り返します。
以上の畳み込み層での計算を式にします。
入力:$U \in \mathbb{R}^{W \times W \times S}$
カーネル:$K \in \mathbb{R}^{3 \times 3 \times S \times T}$
出力:$V \in \mathbb{R}^{(W-2) \times (W-2) \times T}$
として$V$の各成分は
$$
V_{xyt} = \sum_{-1\le i,j\le 1} \sum_{s=1}^S K_{ijst} U_{(x+i)(y+j)s}
$$
見るだけでも痛々しい式です。
$V$は3次元テンソル(三次元配列)で$1 \le x,y \le W-2, \ 1 \le t \le T$で$V_{xyt}$をすべて計算しろというわけですね。
画像のサイズは$W = 256$から始まってプーリング層を通すと128, 64と小さくなりますが、
$S,T$は64や512などCNNを複雑にすればするほど大きな値を取ります。
テンソルの低ランク近似
カーネルは画像の特徴を捉えていて、例えば先ほどの3x3のカーネルでは、
K=
\begin{bmatrix}
0 & 0 & 0 \\
1 & 1 & 1 \\
0 & 0 & 0
\end{bmatrix}
は画像中の横方向に伸びる線の特徴抽出ができます。ここで、
K=
\begin{bmatrix}
0 \\
1 \\
0
\end{bmatrix}
\begin{bmatrix}
1 & 1 & 1
\end{bmatrix}
なので
\beta_1 =
\begin{bmatrix}
0 \\
1 \\
0
\end{bmatrix}, \
\beta_2 =
\begin{bmatrix}
1 \\
1 \\
1
\end{bmatrix}
, \ \
K = \beta_1 \otimes \beta_2 , \ \ K(i,j) = \beta_1(i) \beta_2(j)
となります。つまり、2次元配列(行列)$K$が1次元ベクトル2つ($\beta_1, \beta_2$)のテンソル積で書けて、$K$の$(i,j)$成分は$\beta_1$の$i$番目の要素と$\beta_2$の$j$番目の要素を掛け算です。
これは$K$がランク1の行列であることを表します。
また、一般にランク$R$の行列は
K = \sum_{r=1}^R \beta_1^{r} \otimes \beta_2^{r}, \ K(i,j) = \sum_{r=1}^R \beta_1^{r}(i) \beta_2^{r}(j)
で書けます。
さて、実際の畳み込み層のカーネル$K \in \mathbb{R}^{3 \times 3 \times S \times T}$に話を戻すと、ここでもカーネルが画像の特徴を捉えているならば、そう複雑にはならないため、ランク$R$テンソルでの低ランク近似を行います。
K \in \mathbb{R}^{3 \times 3 \times S \times T}, \ \ K \fallingdotseq \sum_{r=1}^R \beta_1^{r} \otimes \beta_2^{r} \otimes \beta_3^{r} \otimes \beta_4^{r}
$
\beta_1^r \in \mathbb{R}^3, \beta_2^r \in \mathbb{R}^3, \beta_3^r \in \mathbb{R}^S, \beta_4^r \in \mathbb{R}^T \ (r = 1...R)
$として、$K$の各要素は
$$
K(i,j,s,t) = \sum_{r = 1}^R \beta_1^{r}(i) \ \beta_2^{r}(j) \ \beta_3^{r}(s) \ \beta_4^{r}(t)
$$
のようにベクトル$\beta_1^r...\beta_4^r$の中の要素を1つずつ選んで掛け算して得られます。
ここで嬉しいお知らせがあって、元々の$K$のパラメータ数は$3 \times 3 \times S \times T$ でしたが、低ランク近似後の$K$のパラメータ数は$R \times (3 + 3 + S + T)$に落ちます。非常に省メモリですね。
畳み込み層の軽量化
このままだと
「結局計算するには$\beta_1^r...\beta_4^r$から$K$を復元して大きな畳み込み層を計算する必要があるのか?」
という状態ですが、ここも解決されています。
元の畳み込み層の式に低ランク近似の式を代入すると
$$
V_{xyt} = \sum_{-1\le i,j\le 1} \sum_{s=1}^S \sum_{r = 1}^R \beta_1^{r}(i) \ \beta_2^{r}(j) \ \beta_3^{r}(s) \ \beta_4^{r}(t) U_{(x+i)(y+j)s}
$$
この計算順序を並び替えると
$$
V_{xyt} = \sum_{r = 1}^R\beta_4^{r}(t) \sum_{-1\le i \le 1}\beta_1^{r}(i) \sum_{-1\le j \le 1} \beta_2^{r}(j) \
\sum_{s=1}^S \beta_3^{r}(s)\ U_{(x+i)(y+j)s}
$$
この式を後ろから解いていきます。
-
まず$U$は2次元の画像を$S$チャネル重ねたものですが、各チャネルを$\beta_3^{r}(s)$で重み付けした和を計算して2次元の画像にします。(1x1xSのカーネルを用いた畳み込み)
-
この2次元の画像を$\beta_2^{r}$という1x3のカーネルで畳み込み、その後$\beta_1^{r}$という1x3のカーネルで畳み込みます。
-
これを$r=1 ... R$で繰り返し、最後にそのR個の出力を$\beta_3^{r}(t)$で重み付けした和を計算して出力します。(1x1xRのカーネルを用いた畳み込み)
これを出力チャネル分$t=1...T$で計算すると元の畳み込み層で得たい出力が得られます。
畳み込み層の計算の実装はこれまで数々の先人たちが色々効率化してくれていますが、元々3x3xSxTのカーネルで畳み込む必要があったことに比べると、より小さいカーネルを用いた畳み込みで計算でき、CPUにもやさしい計算になっています。
実際の挙動
論文内の結果をまとめます
- カーネルを低ランク近似しているので、劣化します
- ただし、分類問題を解くには出力層で確率最大のラベルを選べばよいので、全体の精度はあまり落ちません
- 36クラス分類では、正解率を90%から91%の悪化に留めて8.5倍の高速化
- AlexNetを用いたImageNetの画像分類では2層目の畳み込み層の置換しtop-5 accuracyを1%の悪化で4倍の高速化
人生そう美味しい話はなく、速さと精度はどちらかしか選べないようですね。
終わりに
テンソル分解を用いた畳み込み層のカーネルの低ランク近似により、CNNの省メモリ・高速化が行えます。
ここでは2次元の畳み込み層を扱いましたが、全く同様にして3次元の畳み込み層にも拡張ができ、パラメータを削減できます。
また、記事内で用いた$K$のテンソル分解はCP分解で、Tucker分解という別のテンソル分解でも似たように畳み込み層の効率化が可能で[Kim et al. ICLR 2016]、こちらも前述のJupyterNotebookで動かせます。
テンソル分解と機械学習については冒頭で引用した方のスライドが参考になります!
高精度ながら莫大な電気を食う深層学習を、どうアルゴリズム上の工夫で省エネ化するかは重要な技術で、今後も発展が期待されます👀