はじめに
時系列データの扱いに特化したディープラーニングのモデルであるリカレントニューラルネットワーク(Recurrent Neural Networks:RNN)に関する学習をしても,結局はTensorflowやKeras,Pytorchといったライブラリに頼った実装がほとんどです.
これらのライブラリを使用した実装は簡単ですが,実際にどのような計算が行われているのかは数式などを眺めることでしか理解できません.
そこで,今回はこれらのライブラリを利用せず,numpyのみで実装を行おうと考えました.
あくまでも,理解を深めるためにNumpyでRNNを実装しているだけなので,「理論が知りたい!」,「どうやったら精度が良くなるの?」という方にはお勧めしません.
「NumpyでRNN実装しようと思っているんだけど,参考になるサイトないかな〜」って人におすすめです.
目次
- RNNの理論
- Pytorchでの実装
- Numpyでの実装
- まとめ
1. RNNの理論
正直,理論面にそこまで詳しくないので,細かい式の導出だったりは専門書にお任せするとして,ここでは実装に必要となるものに限って記載をしたいと思います.
視覚的に捉える
RNNを視覚的に捉えるために,以下の図を載せます.
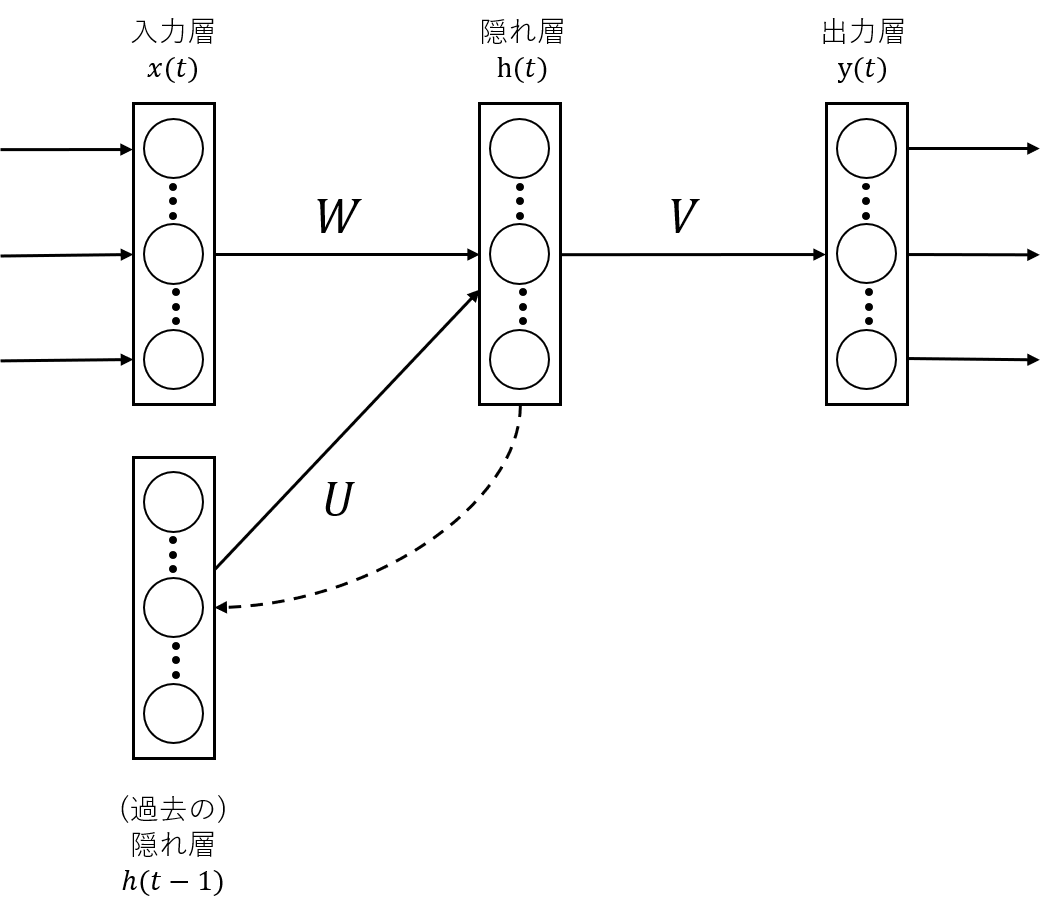
RNNは通常のNNの入力層に過去の隠れ層が増えているだけのシンプルな構造です.
つまりは,$t$時点の入力$x(t)$を隠れ層に伝搬させる際に,$t-1$時点の隠れ層$h(t-1)$も一緒に入力として扱う感じです.
上記の図で見ると,毎回出力している形に見えますが,ここは問題によって調整していくんだと思います.
数学的に捉える
各層での出力を考えてみます.
$t$時点での隠れ層の出力$h(t)$は,
h(t) = f(Wx(t) + Uh(t-1) + \boldsymbol{b})
ここで,$f$は活性化関数,$W$と$U$は重み,$\boldsymbol{b}$はバイアスベクトルです.
次に出力層での出力は,$h(t)$を用いて,
y(t) = g(Vh(t) + \boldsymbol{c})
となる.ここで,$g$は活性化関数,$V$は重み,$\boldsymbol{c}$はバイアスベクトルです.
ここで,誤差関数を$E:=E(W, U, V, \boldsymbol{b}, \boldsymbol{c})$として,それぞれのパラメータに対する勾配を考える.
隠れ層,出力層の活性化前までの値を$\boldsymbol{p}(t)$, $\boldsymbol{q}(t)$で定義する.
\displaylines{
\boldsymbol{p}(t) := Wx(t) + Uh(t-1) + \boldsymbol{b} \\
\boldsymbol{q}(t) := Vh(t) + \boldsymbol{c}
}
すると,隠れ層,出力層における誤差項
\displaylines{
\boldsymbol{e}_h(t) := \frac{\partial E}{\partial \boldsymbol{p}(t)} \\
\boldsymbol{e}_o(t) := \frac{\partial E}{\partial \boldsymbol{q}(t)}
}
に対して,
\displaylines{
\frac{\partial E}{\partial W} = \frac{\partial E}{\partial \boldsymbol{p}(t)}(\frac{\partial \boldsymbol{p}(t)}{\partial W})^T = \boldsymbol{e}_{h(t)} \boldsymbol{x}(t)^T \\
\frac{\partial E}{\partial V} = \frac{\partial E}{\partial \boldsymbol{q}(t)}(\frac{\partial \boldsymbol{q}(t)}{\partial V})^T = \boldsymbol{e}_{o(t)} \boldsymbol{h}(t)^T \\
\frac{\partial E}{\partial U} = \frac{\partial E}{\partial \boldsymbol{p}(t)}(\frac{\partial \boldsymbol{p}(t)}{\partial U})^T = \boldsymbol{e}_{h(t)} \boldsymbol{h}(t-1)^T
}
\displaylines{
\frac{\partial E}{\partial \boldsymbol{b}} = \frac{\partial E}{\partial \boldsymbol{p}(t)}\frac{\partial \boldsymbol{p}(t)}{\partial \boldsymbol{b}} = \boldsymbol{e}_h(t)\\
\frac{\partial E}{\partial \boldsymbol{c}} = \frac{\partial E}{\partial \boldsymbol{q}(t)}\frac{\partial \boldsymbol{p}(t)}{\partial \boldsymbol{c}} = \boldsymbol{e}_o(t)
}
が求まり,$\boldsymbol{e}_h(t)$と$\boldsymbol{e}_o(t)$の誤差項のみを考えれば良いことがわかります.
RNNの誤差を求める際,ネットワークの順伝播で時刻$t-1$における隠れ層の出力$h(t-1)$を考えたため,逆伝播の際も$t-1$における誤差を考える必要がある点に注意する必要があります.
BPTT(Backpropagation Through Time) という手法を使うと$\boldsymbol{e}_h(t-1)$を$\boldsymbol{e}_h(t)$で表すことができます.
(こちらの細かいところについては,ちょっとここでは触れずに,パラメータの更新式だけもらいます)
\displaylines{
W(t + 1) = W(t) - \eta \sum_{z=0}^{\tau}\boldsymbol{e}_h(t-z)\boldsymbol{x}(t-z)^T \\
U(t + 1) = U(t) - \eta \sum_{z=0}^{\tau}\boldsymbol{e}_h(t-z)\boldsymbol{h}(t-z-1)^T \\
V(t + 1) = V(t) - \eta \boldsymbol{e}_o(t) \boldsymbol{h}(t)^T \\
\boldsymbol{b}(t+1) = \boldsymbol{b} - \eta \sum_{z=0}^{\tau}\boldsymbol{e}_h(t-z) \\
\boldsymbol{c}(t+1) = \boldsymbol{c} - \eta \boldsymbol{e}_o (t)
}
2. Pytorchでの実装
Pytorchでの実装は詳解ディープラーニング 第2版 ~TensorFlow/Keras・PyTorchによる時系列データ処理を参考にしています.
(Pytorchでの実装は,こちらの記事の主なる内容ではないの簡潔に記載させていただきます.)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.utils import shuffle
import torch
import torch.nn as nn
import torch.optim as optimizers
# from keras.callbacks import EarlyStopping
class EarlyStopping:
"""earlystoppingクラス"""
def __init__(self, patience=5, verbose=False, path='checkpoint_model.pth'):
"""引数:最小値の非更新数カウンタ、表示設定、モデル格納path"""
self.patience = patience #設定ストップカウンタ
self.verbose = verbose #表示の有無
self.counter = 0 #現在のカウンタ値
self.best_score = None #ベストスコア
self.early_stop = False #ストップフラグ
self.val_loss_min = np.Inf #前回のベストスコア記憶用
self.path = path #ベストモデル格納path
def __call__(self, val_loss, model):
"""
特殊(call)メソッド
実際に学習ループ内で最小lossを更新したか否かを計算させる部分
"""
score = -val_loss
if self.best_score is None: #1Epoch目の処理
self.best_score = score #1Epoch目はそのままベストスコアとして記録する
self.checkpoint(val_loss, model) #記録後にモデルを保存してスコア表示する
elif score < self.best_score: # ベストスコアを更新できなかった場合
self.counter += 1 #ストップカウンタを+1
if self.verbose: #表示を有効にした場合は経過を表示
print(f'EarlyStopping counter: {self.counter} out of {self.patience}') #現在のカウンタを表示する
if self.counter >= self.patience: #設定カウントを上回ったらストップフラグをTrueに変更
self.early_stop = True
else: #ベストスコアを更新した場合
self.best_score = score #ベストスコアを上書き
self.checkpoint(val_loss, model) #モデルを保存してスコア表示
self.counter = 0 #ストップカウンタリセット
def checkpoint(self, val_loss, model):
'''ベストスコア更新時に実行されるチェックポイント関数'''
if self.verbose: #表示を有効にした場合は、前回のベストスコアからどれだけ更新したか?を表示
print(f'Validation loss decreased ({self.val_loss_min:.6f} --> {val_loss:.6f}). Saving model ...')
torch.save(model.state_dict(), self.path) #ベストモデルを指定したpathに保存
self.val_loss_min = val_loss #その時のlossを記録する
class RNN(nn.Module):
def __init__(self, hidden_dim):
super().__init__()
self.l1 = nn.RNN(1, hidden_dim,
nonlinearity="tanh",
batch_first=True)
self.l2 = nn.Linear(hidden_dim, 1)
nn.init.xavier_normal_(self.l1.weight_ih_l0)
nn.init.orthogonal_(self.l1.weight_hh_l0)
def forward(self, x):
h, _ = self.l1(x)
y = self.l2(h[:, -1])
return y
if __name__ == '__main__':
np.random.seed(123)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
"""
1. データの準備
"""
def sin(x, T=100):
return np.sin(2.0 * np.pi * x / T)
def toy_problem(T=100, ampl=0.05):
x = np.arange(0, 2*T + 1)
noise = ampl * np.random.uniform(low=-1.0, high=1.0, size=len(x))
return sin(x) + noise
T = 100
f = toy_problem(T).astype(np.float32)
length_of_sequences = len(f)
maxlen = 25
x = []
t = []
for i in range(length_of_sequences - maxlen):
x.append((f[i:i+maxlen]))
t.append(f[i+maxlen])
x = np.array(x).reshape(-1, maxlen, 1)
t = np.array(t).reshape(-1, 1)
x_train, x_val, t_train, t_val = train_test_split(x, t, test_size=0.2, shuffle=False)
"""
2. モデルの構築
"""
model = RNN(50).to(device)
"""
3. モデルの学習
"""
criterion = nn.MSELoss(reduction="mean")
optimizer = optimizers.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.009), amsgrad=True)
def compute_loss(t, y):
return criterion(y, t)
def train_step(x, t):
x = torch.Tensor(x).to(device)
t = torch.Tensor(t).to(device)
model.train()
preds = model(x)
loss = compute_loss(t, preds)
optimizer.zero_grad()
loss.backward()
optimizer.step()
return loss, preds
def val_step(x, t):
x = torch.Tensor(x).to(device)
t = torch.Tensor(t).to(device)
model.eval()
preds = model(x)
loss = criterion(preds, t)
return loss, preds
epochs = 1000
batch_size = 100
n_batches_train = x_train.shape[0] // batch_size + 1
n_batches_val = x_val.shape[0] // batch_size + 1
hist = {"loss": [], "val_loss": []}
es = EarlyStopping(patience=10, verbose=True)
for epoch in range(epochs):
train_loss = 0.
val_loss = 0.
x_, t_ = shuffle(x_train, t_train)
for batch in range(n_batches_train):
start = batch * batch_size
end = start + batch_size
loss, _ = train_step(x_[start:end], t_[start:end])
train_loss += loss.item()
for batch in range(n_batches_val):
start = batch * batch_size
end = start + batch_size
loss, _ = val_step(x_val[start:end], t_val[start:end])
val_loss += loss.item()
train_loss /= n_batches_train
val_loss /= n_batches_val
hist["loss"].append(train_loss)
hist["val_loss"].append(val_loss)
print("epoch: {}, loss: {:.3f}, val_loss: {:.3f}".format(epoch+1, train_loss, val_loss))
if es(val_loss, model):
break
"""
4. モデルの評価
"""
model.eval()
sin = toy_problem(T, ampl=0.)
gen = [None for i in range(maxlen)]
z = x[:1]
for i in range(length_of_sequences - maxlen):
z_ = torch.Tensor(z[-1:]).to(device)
preds = model(z_).data.cpu().numpy()
z = np.append(z, preds)[1:]
z = z.reshape(-1, maxlen, 1)
gen.append(preds[0, 0])
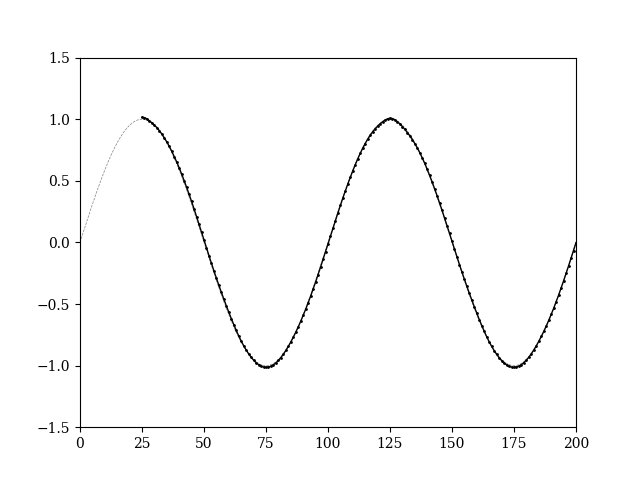
# 予測値を可視化
fig = plt.figure()
plt.rc("font", family="serif")
plt.xlim([0, 2*T])
plt.ylim([-1.5, 1.5])
plt.plot(range(len(f)), sin, color="gray", linestyle="--", linewidth=0.5)
plt.plot(range(len(f)), gen, color="black", linewidth=1, marker="o", markersize=1, markerfacecolor="black", markeredgecolor="black")
plt.show()
この中でRNNを定義しているのは,たったこれだけですね
class RNN(nn.Module):
def __init__(self, hidden_dim):
super().__init__()
self.l1 = nn.RNN(1, hidden_dim,
nonlinearity="tanh",
batch_first=True)
self.l2 = nn.Linear(hidden_dim, 1)
nn.init.xavier_normal_(self.l1.weight_ih_l0)
nn.init.orthogonal_(self.l1.weight_hh_l0)
def forward(self, x):
h, _ = self.l1(x)
y = self.l2(h[:, -1])
return y
そして,どんな計算がなされているのか全くわからない...
ということでNumpyで実装する訳ですね.
ちなみに学習させたモデルで,新たに$sin$を予測させると
良きですね.
3. Numpyでの実装
Numpyでの実装についてはhttps://github.com/Javicadserres/quantdare_postsを参考にしています.
モデルの定義
パラメータの初期化を行います.
class RNN:
def __init__(self, input_dim, output_dim, hidden_dim):
self.input_dim = input_dim
self.output_dim = output_dim
self.hidden_dim = hidden_dim
params = self._initialize_params(input_dim, output_dim, hidden_dim)
self.V = params[0]
self.W = params[1]
self.U = params[2]
self.c = params[3]
self.b = params[4]
self.activation = Activation()
self.oparams = None
def _initialize_params(self, input_dim, output_dim, hidden_dim):
den = np.sqrt(hidden_dim)
weights_V = np.random.randn(output_dim, hidden_dim) / den
bias_c = np.zeros((output_dim, 1))
weights_W = np.random.randn(hidden_dim, input_dim) / den
weights_U = np.random.randn(hidden_dim, hidden_dim) / den
bias_b = np.zeros((hidden_dim, 1))
return [weights_V, weights_W, weights_U, bias_c, bias_b]
次に順伝播を記載します.
def foward(self, x):
self.x = x
self.layers_tanh = [Tanh() for _ in x]
hidden = np.zeros((self.hidden_dim, 1))
self.hidden_list = [hidden]
self.y_preds = []
for input_x, layer_tanh in zip(x, self.layers_tanh):
input_tanh = np.dot(self.W, input_x) + np.dot(self.U, hidden) + self.b
hidden = layer_tanh.forward(input_tanh)
self.hidden_list.append(hidden)
input_activation = np.dot(self.V, hidden) + self.c
y_pred = self.activation.forward(input_activation)
self.y_preds.append(y_pred)
return self.y_preds
$h(t) = f(Wx(t) + Uh(t-1) + \boldsymbol{b})$,$y(t) = g(Vh(t) + \boldsymbol{c})$の計算をそれぞれ
input_tanh = np.dot(self.W, input_x) + np.dot(self.U, hidden) + self.b
と
input_activation = np.dot(self.V, hidden) + self.c
で行っています.
誤差の計算をします.ここでは2乗誤差関数を用いました.
E := \frac{1}{2} \sum_{t=1}^{T} || y(t) - t(t) || ^2
def loss(self, Y):
"""
SSE
:param Y:
:return:
"""
self.Y = Y
self.layers_loss = [SSE() for _ in Y]
cost = 0
for y_pred, y, layer in zip(self.y_preds, self.Y, self.layers_loss):
cost += layer.forward(y_pred, y)
return cost
逆伝播の記載をしていきます.
def backward(self):
"""
backward propagation
:return:
"""
gradients = self._define_gradients()
self.dW, self.dU, self.dV, self.db, self.dc, dhidden_next = gradients
for index, layer_loss in reversed(list(enumerate(self.layers_loss))):
dy = layer_loss.backward()
# hidden actual
hidden = self.hidden_list[index + 1]
hidden_prev = self.hidden_list[index]
# gradients y
self.dV += np.dot(dy, hidden.T)
self.dc += dy
dhidden = np.dot(self.V.T, dy) + dhidden_next
# gradients a
dtanh = self.layers_tanh[index].backward(dhidden)
self.db += dtanh
self.dW += np.dot(dtanh, self.x[index].T)
self.dU += np.dot(dtanh, hidden_prev.T)
dhidden_next = np.dot(self.U.T, dtanh)
def _define_gradients(self):
dW = np.zeros_like(self.W)
dU = np.zeros_like(self.U)
dV = np.zeros_like(self.V)
db = np.zeros_like(self.b)
dc = np.zeros_like(self.c)
da_next = np.zeros_like(self.hidden_list[0])
return dW, dU, dV, db, dc, da_next
sin波の学習
モデルを定義したところで,実際にsin波の学習をするコードを記述していきます.
まずは,おまじないをします.
if __name__ == '__main__':
"""
0. 初期化
"""
np.random.seed(1)
続いてデータの準備を行います.今回はsin波にノイズを加えたものを使用します.(pytorchでの実装に使用したものと同じ定義をします)
"""
1. データの準備
"""
def sin(x, T=100):
return np.sin(2.0 * np.pi * x / T)
def add_noise(T=100, noise_level=0.01):
x = np.arange(0, 2*T + 1)
noise = noise_level * np.random.uniform(low=-1.0, high=1.0, size=len(x))
return sin(x) + noise
T = 100
f = add_noise(T).astype(np.float32)
length = len(f)
どれだけ過去を振り返るか,今回は$5$にしておきましょう.
maxlen = 5
次に,データを分けていきます.
x = []
t = []
for i in range(length - maxlen):
x.append((f[i:i+maxlen]))
t.append(f[i+maxlen])
x = np.array(x).reshape(-1, maxlen, 1)
t = np.array(t).reshape(-1, 1)
target_length = len(t)
軽く例をあげて解説すると,次のような時系列データがあったとします.
1, 4, 9, 16, 25, 36, 49
この時,先程のプログラムを実行させると,次のような配列が出来上がります.
\displaylines{
x:[1, 4, 9, 16, 25], \ t:[36] \ (index=1) \\
x:[4, 9, 16, 25, 36], \ t:[49] \ (index=2)
}
$5$時点分のデータと.その次にくるデータを表すことができます.
(日本語不自由ですね,すみません)
データセットを作成したので,trainデータとtestデータに分割していきます.
(癖で分割してしまいましたが,今回は精度を極めるのではなく,学習さえできていればいいので,testデータは使いません)
# trainデータとtestデータに分割
x_train, x_val, t_train, t_val = train_test_split(x, t, test_size=0.2, shuffle=False)
次にモデルの構築を行います.
"""
2. モデル構築
"""
input_dim = 1
output_dim = 1
hidden_dim = 50
model = RNN(input_dim, output_dim, hidden_dim)
optim = SGD(lr=0.01)
optimizerとしてSGDを使います.
では,実際にモデルの学習を行っていきましょう.
"""
3. モデルの学習
"""
epochs = 1000
hist = []
for epoch in range(epochs):
index = epoch % len(x_train)
X = x_train[index]
Y = t_train[index]
X = X.reshape(len(X), 1, -1)
y_preds = model.foward(X)
cost = model.loss(Y)
model.backward()
# optimize
model.optimize(optim)
print("Cost after iteration %d: %f" % (epoch, cost))
hist.append(cost)
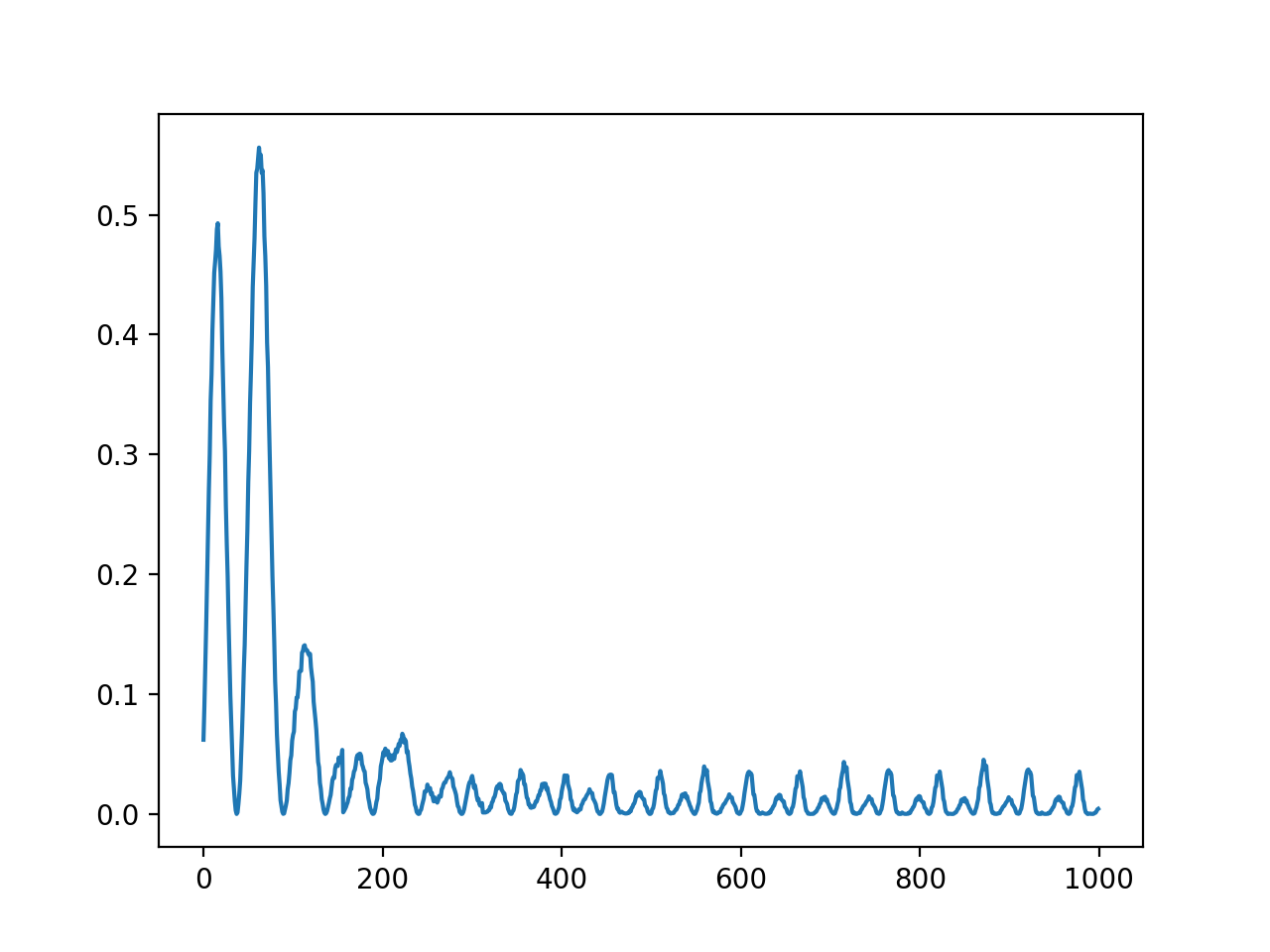
plt.plot([i for i in range(len(hist))], hist)
plt.show()
誤差をグラフで表すと,良い感じに$0$に近づいている感じがしますね.
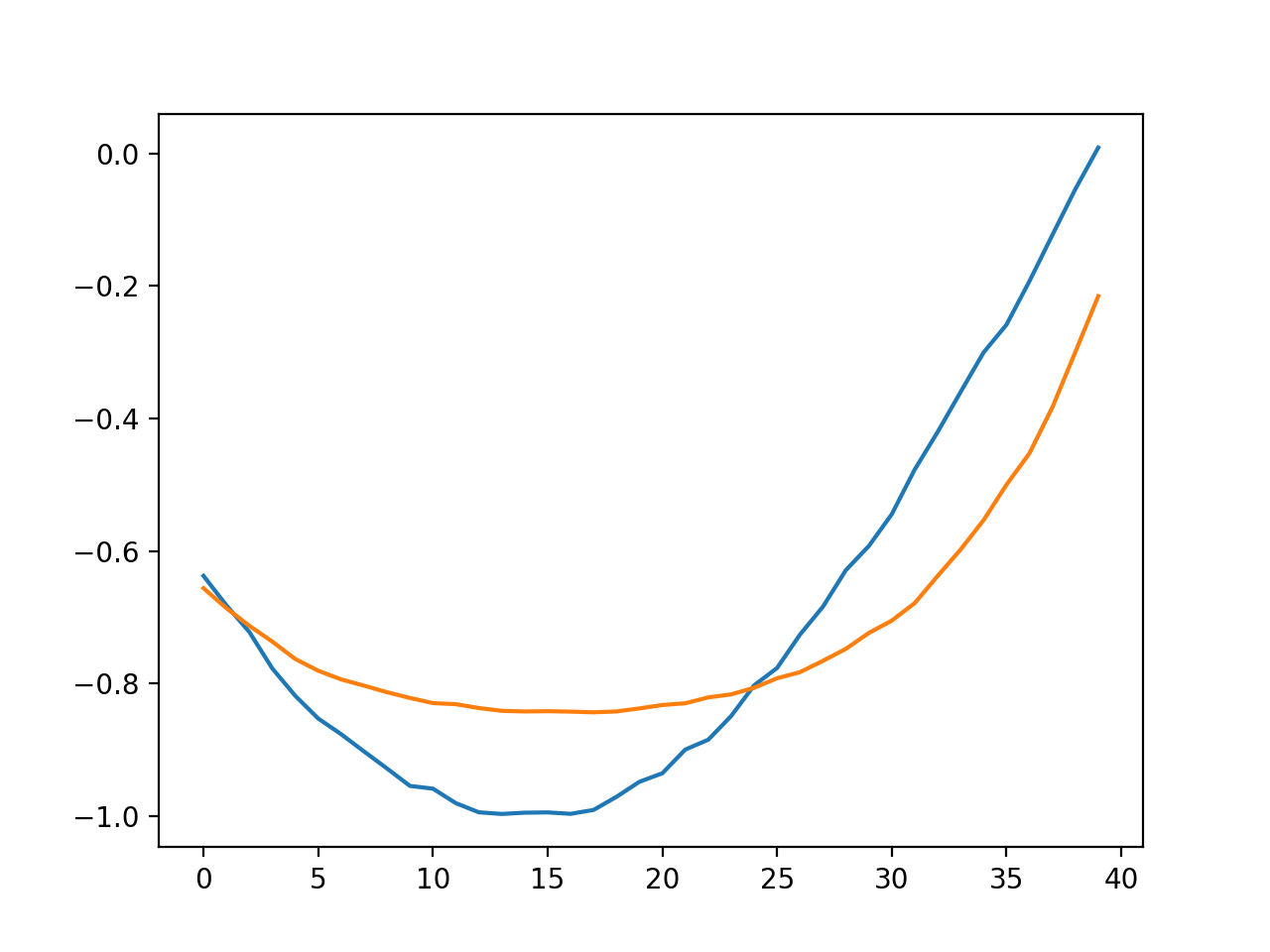
一応,データをtrainとtestに分けていたので,testデータを使って予測してみました.
青が実際の値で,オレンジが学習させたモデルを使って出した予測ですね.
一応予測できてるかな?って感じだと思います.
4. まとめ
かなり緩く,数学的なところもかなり省略しましたが,当初の目標であるNumpyでRNNを実装するというのは達成されました.
色々と指摘はあると思うのですが,あくまでも「NumpyでRNNを実装する」というのが目標なので,細かいところは気にしないでください...