LoginSignup
33
41

More than 3 years have passed since last update.

@hotaru_77(Kei Takamoto)

量子コンピュータによる機械学習に載っている機械学習手法を実装してみました

Last updated at Posted at 2021-02-13

目次

  1. はじめに
  2. ベイジアンネットワーク
  3. 隠れマルコフモデル
  4. カーネル密度推定
  5. k近傍法
  6. サポートベクターマシーン
  7. まとめ

はじめに

機械学習の勉強を始めようと参考書を開くと様々な手法が次々と紹介されていて，少々困惑してしまいました．そこでそれぞれの手法を実際に実装しながら調べたりすることで理解を深めようと思いました．正直pythonのライブラリを使った実装なので細かい理論までは追えていませんがそこは追々ということにしておきます．

ベイジアンネットワーク

ベイジアンネットワークとは条件つき独立性を仮定した確率モデルであり，$p(s)$の扱いを平易にする．

細かい理論については置いておいて，この記事では実装することを目標にpgmpyを用いて実装していきます．

問題設定

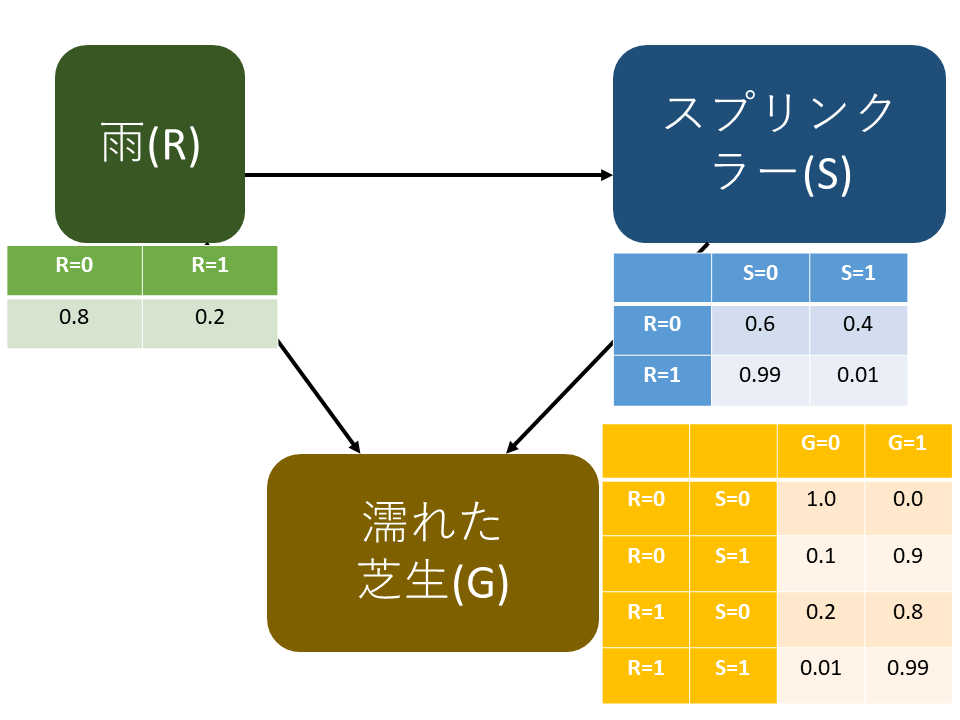
上記のような問題を考えます．
緑の表での$R=0$は雨が降らない確率を，$R=1$は雨が降る確率を表しています．
青の表ではスプリンクラーが作動しない確率$S=0$と作動する確率$S=1$を$R=0$の時，$R=1$の時で別々で与えたいます．黄色の表に関しても同様です．

ベイジアンネットワークの実装

では実際に上記の図をベイジアンネットワークで作成していきます．

Bayesian.py
# ライブラリのimport
from pgmpy.factors.discrete import TabularCPD
from pgmpy.models import BayesianModel
from pgmpy.inference import VariableElimination


## ベイジアンネットワークの構造
model = BayesianModel([
    # ('親ノード', '子ノード')
    ('rain', 'sprinkler'),
    ('rain', 'grass'),
    ('sprinkler', 'grass'),
])

rain_cpd = TabularCPD(
    variable='rain',
    variable_card=2,
    values=[[.8], [.2]])

sprinkler_cpd = TabularCPD(
    variable='sprinkler',
    variable_card=2,
    values=[[.6, 0.99], [.4, 0.01]],
    evidence=['rain'],
    evidence_card=[2])

grass_cpd = TabularCPD(
    variable='grass',
    variable_card=2,
    values=[[1.0, 0.1, 0.2, 0.01], [0.0, 0.9, 0.8, 0.99]],
    evidence=['rain', 'sprinkler'],
    evidence_card=[2, 2])

model.add_cpds(rain_cpd, sprinkler_cpd, grass_cpd)

ベイジアンネットワークで推論

実装したベイジアンネットワークを使って推論を行ってみます．
ここでは芝生が濡れていないときの雨が降っていない確率と降っている確率を求めます．

model_infer = VariableElimination(model)
rain0_given_grass1 = model_infer.query(variables=['rain'], evidence={'grass': 0})
print(rain0_sprinkler1_given_grass1)

結果は

+---------+-------------+
| rain    |   phi(rain) |
+=========+=============+
| rain(0) |      0.9282 |
+---------+-------------+
| rain(1) |      0.0718 |
+---------+-------------+

となりました．

ここではベイジアンネットワークを作成し，推論を行いましたが，

実際にベイジアンネットワークを推定することは，一般的に難しい問題とされている．

隠れマルコフモデル

隠れマルコフモデルは，「連鎖したイベント」のシーケンスを表すという点でベイジアンネットワークと性質が多少異なるグラフィカルモデルである．

こちらも細かい理論については置いておいて，この記事では実装することを目標にhmmlearnを用いて実装していきます．

モデルの構築

隠れマルコフモデルには三つのパラメータがあります．

  1. 初期状態確率$\pi$
  2. 遷移確率$A$
  3. 出力確率$B$

これらのパラメータは学習で推定することができるが，明示的に指定してモデルを構築することもできる．

hmm1.py
from hmmlearn import hmm
import numpy as np


model = hmm.GaussianHMM(n_components=5, covariance_type='full')

# 初期状態確率π（q_iが初期状態である確率）
model.startprob_ = np.array([0.1, 0.1, 0.7, 0.0, 0.1])

# 状態遷移確率
model.transmat_ = np.array([[0.9, 0.1, 0.0, 0.0, 0.0],
                           [0.4, 0.3, 0.3, 0.0, 0.0],
                           [0.1, 0.2, 0.4, 0.3, 0.0],
                           [0.0, 0.1, 0.3, 0.3, 0.3],
                           [0.0, 0.0, 0.3, 0.1, 0.6]])

# 出力確率の平均と共分散（正規分布に従うと仮定している）
model.means_ = np.array([[1.0, 1.0],
                         [2.0, 2.0],
                         [3.0, 3.0],
                         [4.0, 4.0],
                         [5.0, 5.0]])

model.covars_ = 0.1 * np.tile(np.identity(2), (5, 1, 1))

観測系列のサンプルを得ます．

X, Z = model.sample(10)

# （観測系列，状態系列）
print(X)
print(Z)

[[2.71618377 2.78799886]
 [0.68544061 0.98482839]
 [1.00413618 0.67011749]
 [1.48194136 0.40049633]
 [0.99204692 0.56744503]
 [1.22996837 1.54221408]
 [0.96063165 0.7236326 ]
 [1.09050931 1.02022522]
 [0.62496655 1.79905732]
 [2.16068752 2.01486085]]
[2 0 0 0 0 0 0 0 0 1]

モデルの推定

未知のモデルから観測結果$X$が得られたときのモデルのパラメータ推定を行います．
今回は先ほど得られたXを用いてモデルを推定するので先ほど設定したパラメータと近い結果が出ればよしとなります．

# 未知のモデルから観測結果xが得られたときのモデルのパラメータ推定
remodel = hmm.GaussianHMM(n_components=5, covariance_type='full', n_iter=100)

# 10個じゃ足りないので
X, Z = model.sample(100000)
remodel.fit(X)
print(remodel.transmat_)
print(remodel.means_)

[[8.62112104e-001 1.40414272e-043 4.53692486e-002 9.25186472e-002 4.32192981e-210]
 [9.47989464e-002 3.86113456e-001 1.21180890e-002 2.01738550e-001 3.05230958e-001]
 [7.35799070e-001 1.74156909e-023 6.10442576e-002 2.03156672e-001 5.34486884e-141]
 [3.78574551e-001 2.95087807e-001 2.57058086e-002 3.00631833e-001 3.48102550e-037]
 [4.78719535e-072 2.59776988e-001 6.40756512e-040 5.38660770e-002 6.86356935e-001]]
[[0.99491185 0.99964309]
 [2.98617434 2.99500088]
 [1.08849405 1.04527434]
 [2.00120936 2.00125902]
 [4.37461666 4.36637911]]

正解に近いパラメータが推定できていることが確認できる．パラメータ内のベクトルの並び順はランダムなので注意．

カーネル密度推定

カーネル密度推定(kernel density estimation）は，統計学において，確率変数の確率密度関数を推定する．

データの作成

今回は使用するデータとして2020年横浜市の最高気温のデータを使用します．

kde.py
import numpy as np
from scipy.stats import gaussian_kde
import matplotlib.pyplot as plt

# データの読み込み（今回は2020年横浜市の最高気温のデータを使用）
f = open('data/Yokohama_tmp.txt', 'r')
lines = f.readlines()
data = []
for line in lines:
    data.append(float(line))

# ヒストグラムで表してみます．
plt.hist(data, bins=30, range=(6, 37), color='orange')
plt.xlabel('temperature')
plt.ylabel('days')
plt.show()

kde_hist.png

推定

このデータを用いて推定を行っていきます．

# gaussian_kdeのインスタンスを作成
kde = gaussian_kde(data)

# 6〜37で密度推定
estimate = kde(np.linspace(6, 37, num=32), bw_method=0.2![kde.png]
# グラフで表示
plt.plot([x for x in range(6, 38)], estimate)
plt.xlabel('temperature')
plt.ylabel('kde')
plt.show()

kde.png

k近傍法

k近傍法(K-Nearest Neighbor)は，k個の近傍点を囲むある半径を持った一定値のカーネルによるカーネル密度推定として捉えることができる．

つまりは特徴空間において近くにあるk個のオブジェクトのうち最も一般的なクラスに分類します．
kの値が小さいとノイズの影響を受けやすくなり，kの値が大きいと精度が落ちる．

実装

分類するデータとしてアヤメの花を使用します．
kを変えながら精度を確認していきます．

knn.py
import matplotlib.pyplot as plt

from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier

# アヤメデータセット読み込み
from sklearn.datasets import load_iris
iris = load_iris()

# 特徴量
X = iris.data
# 目的変数
Y = iris.target

# データ分割
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=0)

list_knn = []
scores = []
for k in range(1, 31):
    # K-NN
    knc = KNeighborsClassifier(n_neighbors=k)
    knc.fit(X_train, Y_train)
    # 予測　
    Y_pred = knc.predict(X_test)
    score = knc.score(X_test, Y_test)
    print("[%d] score: {:.2f}".format(score) % k)

    list_knn.append(k)
    scores.append(score)

# プロット
plt.ylim(0.9, 1.0)
plt.xlabel("n_neighbors")
plt.ylabel("score")
plt.plot(list_knn, scores)
plt.show()

knn.png

kが20を超えたあたりから精度が落ちているのがわかります．

サポートベクターマシーン

サポートベクターマシンは，教師あり学習を用いるパターン認識モデルの一つであり，分類や回帰へ適用できる．現在知られている手法の中でも認識性能が優れた学習モデルの一つである．

ここでもsklearnを使用して実装を行っていきます．

実装

今回使用するデータもアヤメの花です．

svm.py
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC

iris = load_iris()

# 説明変数
X = iris.data
# 目的変数
Y = iris.target

# データの分割
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.5, random_state=0)

# モデルを構築
model = SVC(gamma='scale')
model.fit(X_train, Y_train)

# 予測
print(model.score(X_test, Y_test))
"0.9466666666666667"

sklearnを用いて実装するとさっぱりしすぎな気もしますね...

まとめ

それぞれのアルゴリズムが何に用いられるのか．何が難点なのかをまとめてみました．

  • ベイジアンネットワーク

    • 複数の事象間の因果関係をグラフ構造で表現することができる．
    • 既知の情報を元に未知の情報を確率的に知ることができる．
    • ベイジアンネットワークの推定は一般的に難しい．

  • 隠れマルコフモデル

    • 時系列のパターン認識に用いられる．（株価変動の予測，音声認識など）
    • 観測された記号系列の背後に存在する状態の遷移系列を推測する．
    • ニューラルネットワークに隠れマルコフモデルの役割が奪われつつあるが，出力結果の導出過程がわかるという利点もある．

  • カーネル密度推定

    • いくつかの標本から全体の分布を推定することができる．

  • k近傍法

    • クラス判別用の手法．
    • パラメータkに結果が左右される．

  • サポートベクターマシーン

    • パターン認識に用いられる．
    • 分類や回帰に用いられる．
    • 2つのグループに分けるのには優れているが3つ以上のグループに分けるものにはそのまま適用できず計算量が多くなってしまう．

軽くまとめてみました．それぞれの手法がどのような手法であるかに加えてどのような場面に適用できて，どのような利点があるのかを知っておくのは良いことだと思います．

コードはこちらに掲載しています．Github

33
41
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
33
41