統計を学ぶ上で避けて通れない最尤推定とMAP(事後確率最大)推定。
ベイズ推定の土台にもなる重要な推定法です。
それぞれの推定法の違いは理解できた(たぶん)のですが、いざそれぞれの推定方法で計算してみろ!と言われるとまだ固まってしまいます。
そこでその状態から脱するために、各推定のプロセスをPythonで書いてみました。
既に先人の方たちが色んな形で解説してくれているのですが、私はそれらの神ブログと参考書片手にやっと理解できましたw
詳しい解説をしようとすると数式だらけになるので、自分含めた初学者理解の助けにもなる様、意訳を挟みつつ書いてみます。
環境
Ubuntu16.04(Windows10 Bash on Windows)
Python3.6.3(Anaconda5.0.1)
題材
別記事でも書いている「StanとRでベイズ統計モデリング」の5節から例題のデータセットを拝借します。
そしてそのデータをn次多項式で曲線フィッティングしてみましょう。
※本ではやってませんw
※別記事
Pythonで「StanとRでベイズ統計モデリング」の4節をやってみた(PyStan)
【PythonとStanで重回帰】「StanとRでベイズ統計モデリング」の5.1節をやってみた(PyStan)
Github
データの準備&中身チェック
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
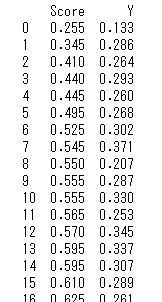
data = pd.read_csv('RStanBook/chap05/input/data-attendance-1.txt') # データセットを読み込む
data.Score /= 200 # スケーリングして絶対値を揃える
# ソート&見やすいデータに絞る(大人の事情)
data = data.sort_values(by='Score')[data.A != 1]
data = data.reset_index().drop('index', axis=1)[['Score', 'Y']]
print(data)
sns.set_style("whitegrid")
sns.set(font_scale=1)
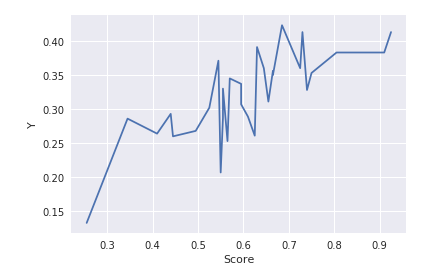
plt.plot(data['Score'], data['Y'])
plt.xlabel('Score')
plt.ylabel('Y')
相関のありそうな曲線(というか折れ線)が得られました。
一部フィッティングむりぽな気がしますが気にせず進めましょう。
※後で知ったのですが、折れ線へのフィッティングは解析的な関数よりも最適化関数などがよいそうですねw
今回はとりあえず3次多項式でフィッティングを目指しますので、n次多項式は下記の通りです。
$y(x,w)=w_0+w_1x^1+w_2x^2+w_3x^3$
簡単に言うと、$Score=x$が与えられた時の$y$を、最適な係数$w0, w1, w2, w3$を求めてフィッティングしていきます。
$y(x,w)$が上の青の曲線にできるだけ重なる様、係数を求めるわけです。
最尤推定
まずは基本中の基本で統計学でもおなじみの最尤推定からやってみます。(基本のキは最小二乗法ですが、途中で出てくるのでそこで触れています)
最尤推定の基本となる式は下記の通り。(βは後に出てくる正規分布の分散)
$argmax$ $p(t|x,w,β)$
$p(t_n|x_n,w,β)$の累積が最大となる$w$が真のパラメータであるとして、$w$の値を決定します。
説明しやすい様にコードをブツ切りにしているので、実行する時は適当に合体させてください。
# 最尤推定
import numpy as np
def main():
x = np.array(data['Score'])
y = np.array(data['Y'])
n = len(x)
# 多項式の係数を推定
w = estimate(x, y)
~中略~
if __name__ == '__main__':
D = 3 # n次多項式の次数
main()
x軸をスコアデータ、y軸を評価データとして変数に格納して推定していきましょう。
まずは観測データから3次多項式の各係数$w$を求めます。
最尤推定では、「得られたデータ = 真のパラメータをもった確率分布からもっとも高い確率で得られるもの」と考えて計算を進めます。
日本語がわかりにくいですが、例えば6回サイコロを振って(1,2,3,6,6,6)が得られたとします。この場合、最尤推定においてそのサイコロは、2分の1の確率で6の目がでて6分の1の確率で1,2,3が出るサイコロと考えます。なぜなら、そのデータは真の確率分布から得られたデータなので、そのデータをもっとも得やすいサイコロこそが真の確率分布だと決めるからです。違和感があると思いますが、そういうものとしておきましょう。
ただ、真の確率分布から得られたデータだとしても誤差が含まれている可能性は否定できない為、その誤差も踏まえて真のパラメータを求めにいきます。その誤差は平均0、分散$β$の正規分布に従っていると仮定すると、観測データの一つ一つは
$y(x_n,w) + ε_n (~ N(0, β))$
で推定できるとします。すなわち
N( y(x,w), β) = \frac{1}{\sqrt{2π}β}exp(-\frac{(y(x,w)−Y)^2}{2β})
から真のパラメータ$w$と$β$が求められることになります。
最尤推定では、上記の式に各値を入れた時の累積確率が最も大きくなるパラメータを真とします(最大尤度)。計算は上記式の対数をとって計算しやすくしてから、各パラメータについて偏微分をして0とおくことで、連立方程式を立て解くことができます。
尚、偏微分の一歩手前(対数をとった後)に出てくるのが下記式なのですが、
lnp(t|x,w,σ)=−\frac{1}{2β}\sum_{k=1}^N \{y(x_n,w) - Y_n\}^2 + \frac{N}{2}ln\frac{1}{β} - \frac{N}{2}ln(2π)
$w$で偏微分を行うと2項目と3項目は定数で消えるので、残るのは最小二乗法と同じ式になります($β$も定数とみなせるので関係なし)。
これはパラメータを求める上で、誤差が平均0の正規分布に従うと仮定した最尤推定と最小二乗法は、やってる計算が同じということです。なので、今回の場合は求まるパラメータ$w$が最小二乗法でも同じものになります。
※誤差を考慮した結果を示せる部分のみ違います
偏微分の結果得られた連立方程式を行列計算にしているのが下記のコードです。
# 観測データから多項式の係数を推定
def estimate(x, y):
# 対数尤度の式を各係数で編微分し、その結果得られる方程式の係数行列を作成
# 係数行列を対称行列へ変形する仮定と同じ(数学知ってる人は偏微分せずこれでもいける)
Sym = []
for i in range(D+1):
for j in range(D+1):
Sym.append((x**(i+j)).sum())
Sym = np.array(Sym).reshape(D+1, D+1)
# 右辺の列ベクトルを作成
R = []
N = len(y)
for i in range(D+1):
tmp = 0
for j in range(N):
tmp += y[j] * x[j]**i
R.append(tmp)
R = np.array(R).T # 行ベクトルから列ベクトルに直さなくても計算はできる
# R = Sym * 変数ベクトル⇒これを求める
W = np.linalg.solve(Sym, R)
return W
これでパラメータ$w$を求めることができました。
後はこのパラメータを使って$Y$の推定値を出し、描画をしてあげれば一旦曲線フィッティングの完了です。
def Y(x, W):
N = len(x)
P = []
# 多項式を計算してるだけ
for i in range(N):
tmp = 0
for j in range(D+1):
tmp += (x[i]**(j)) * W[j]
P.append(tmp)
return np.array(P)
def main():
~中略~
# 推定した係数から予測値を求める
p = Y(x, w)
# 予測値の標準偏差を求める
beta = np.sqrt(((p-y)**2).sum() / n)
print('標準偏差'.format(beta))
# 95%信頼区間
up = p + 1.96*beta
low = p - 1.96*beta
$β$は方程式を$β$で偏微分してあげても良いですし、上記の様に分散の公式に入れてあげても求まります。
最後に描画です。
def main():
~中略~
# 描画
sns.set_style("whitegrid")
sns.set(font_scale=1)
plt.title('{} dimensions'.format(D))
plt.plot(x, y, 'g--', label='observation') # 観測データ
plt.plot(x, p, 'b-' , label='prediction') # 予測データ
plt.plot(x, up, 'y--')
plt.plot(x, low, 'y--')
plt.legend() # ラベルを表示
plt.xlabel('Score')
plt.ylabel('Prediction')
plt.show()
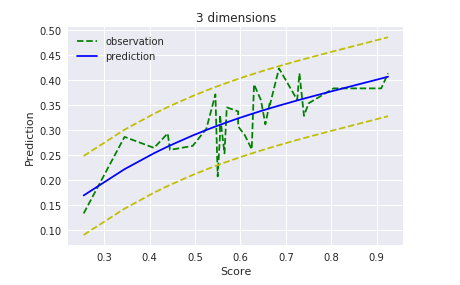
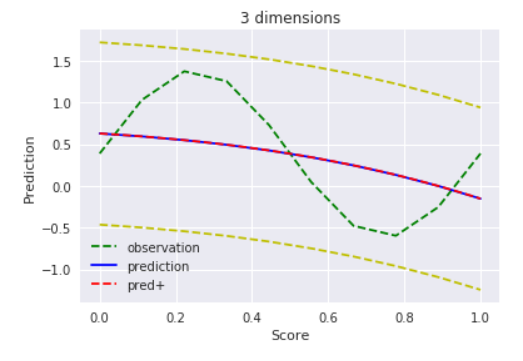
当初の予想通り、細かい部分はフィッティングできてませんが、95%信頼区間には概ね収まっているし、こんなもんでしょう。
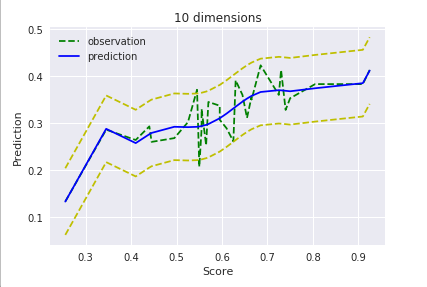
ちなみに次元を増やすとこんな感じ。
$D=10$
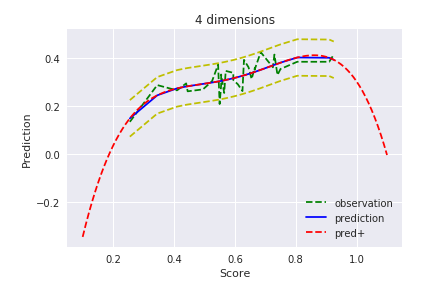
ただ、観測データ範囲外のデータを入れてみるとこうなります。
xp = np.linspace(0.0,1.2,200)
yp = Y(xp, w)
plt.plot(xp, yp, 'r--', label='pred+') # 外挿チェック
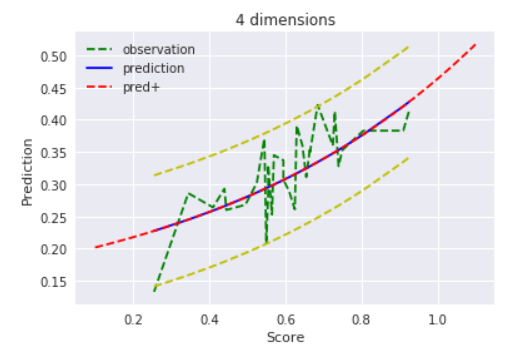
$D=4$
明らかに過学習(観測データのみにフィット)しています。まあ範囲外のデータにフィットさせるのが目的ではないので、使い方が間違っているとも言えますが、それっぽい曲線にはなってほしいですよね。これは後ほどMAP推定でどうなるか見てみましょう。
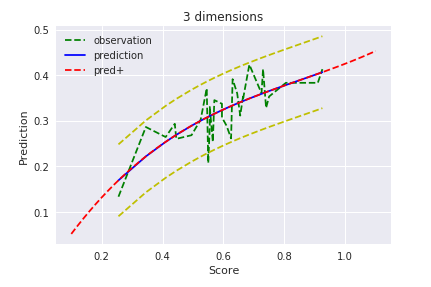
$D = 3$
過学習しない前提で考えると、今回の最尤推定において次数は3が限界かな?
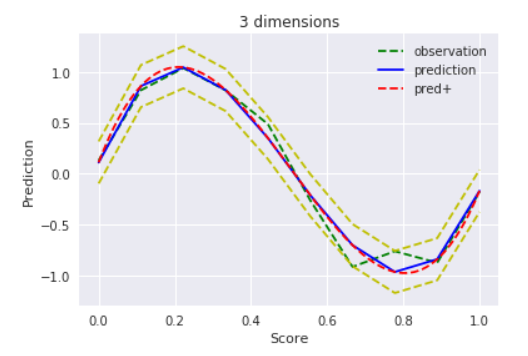
ちなみに同じコードでsin波にフィットさせようとするとこんな感じ
$D = 3$
ええ感じ。
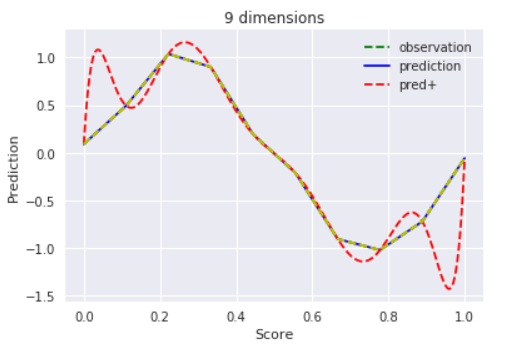
$D = 9$
過学習気味。
以上で最尤推定は完了です。使ってる数式は少ないので、シンプルといえばシンプル。
ただその分、観測データに依存した結果になるので、過学習は避けられなさそうです。必要なデータ量が十分に得られているなら、問題はないんでしょうけどね。
MAP推定
お次は最大事後確率(MAP)推定。
MAP推定を意訳すると、現実を数式でモデリングする際、このパラメータは大体こんな値をとるだろう、ということがわかっていることもありますよね(今回は$w$について)。そうした経験則(主観確率)を事前分布としてパラメータに盛り込むことが可能になるのがMAP推定です。この主観確率が曲者なのですが。。
それではPythonでMAP推定をやってみます。MAP推定の基本となる式は下記の通り。
$p(w|x,t,α,β)∝$ $argmax$ $p(t|x,w,β)p(w|α)$
最尤推定の形と比較して、パラメータ$α$とパラメータ$w$の事前確立$p(w|α)$が追加されています。まずは先で述べた様に$w$の事前分布$=p(w|a)$を決めた上で、事後確率の最大化を行っていきます。
ただ、自分はここで疑問が生まれました。最尤推定では尤度の最大化(実際の観測データが得られる確率が最大となる$w$を求める)と呼んでいたものが、MAP推定では事後確率の最大化に変わります。この2つは何がどう変わったのか、なぜ呼び方が変わったのか?それについて簡単に説明しておきます。
MAP推定では$w$を確率分布として定義して、それを尤度関数(上記の最尤推定だと正規分布の式)にかけます。つまり、尤度が最大となる$w$が求まったら、その$w$が実際に得られる確率もかけ合わせてあげる訳です。重み付けみたいなもんですね。意訳すると、その$w$が実際に発生する確率は何%です!と事前確率が難癖(補足)をつけるんですね。尤度は最大化できるけど現実離れした$w$は、この難癖によって評価が下げられてしまう、とでもいいますか。
これによって、尤度をより大きくするだけでなく、実際に起こりやすい$w$の評価が最も大きくなり、それを真の値として採用するのがMAP推定です。
(わかりにくいかな?w)
MAP推定の式(対数変換済み)を見ると、最尤推定で使っていた尤度の関数に正則化の項を$w$の関数として追加した形になっています。
lnp(t|x,w,β, α)=−\frac{1}{2β}\sum_{k=1}^N \{y(x_n,w) - Y_n\}^2 + \frac{N}{2}lnβ - \frac{N}{2}ln(2π) - \frac{1}{2α}|w|^2
正則化は最小二乗法などで過学習を防ぐ方法の一つです。詳しい説明は割愛しますが、その正則化の役割を最尤推定に追加したのがMAP推定だということが式からわかります。
これをPythonで書くと、先ほどの最尤推定のコードとほとんど変わりません。
$w$を求める連立方程式を行列で表す段階で、行列の対角成分に$\frac{1}{2α}$を足してあげるだけです。なぜそうなるかは、上記の式を$w$で偏微分していくと求まります。
大部分は同様のコードなので、MAP推定の為に追加した部分のみ抜粋します。
# 観測データから多項式の係数を推定
def estimate(x, y, alpha):
# 対数尤度の式を各係数で編微分し、その結果得られる方程式の係数行列を作成
# 係数行列を対称行列へ変形する仮定と同じ(数学知ってる人は偏微分せずこれでもいける)
Sym = []
for i in range(D+1):
for j in range(D+1):
Sym.append((x**(i+j)).sum())
Sym = np.array(Sym).reshape(D+1, D+1)
# *****************追加部分*****************
# 事前分布の行列を作成(対角行列)
Rgl = []
for i in range(D+1):
tmp = np.zeros(D+1)
tmp[i] = 1/alpha
Rgl.append(tmp)
Rgl = np.array(Rgl).reshape(D+1, D+1)
A = Sym+Rgl # ここがMAP推定によって値が変わる部分
# *****************追加部分fin*****************
# 右辺の列ベクトルを作成
R = []
N = len(y)
for i in range(D+1):
tmp = 0
for j in range(N):
tmp += y[j] * x[j]**i
R.append(tmp)
R = np.array(R).T # 行ベクトルから列ベクトルに直さなくても計算はできる
# R = Sym * 変数ベクトル⇒これを求める
W = np.linalg.solve(A, R)
return W
def main():
x = np.array(data['Score'])
y = np.array(data['Y'])
n = len(x)
# *****************追加部分*****************
alpha = 1 # wの事前分布の分散
# 多項式の係数を推定
w = estimate(x, y, alpha)
変更点は$w$の事前分布の分散である$α$を加算しているところです。
計算を見るとわかりますが、分散が大きいほど$w$がとり得る値の範囲が大きくなるので、正則化の値は0に近くなり、最尤推定の結果とほとんど変わらなくなります。逆に、分散が小さいほど$w$のとり得る値の範囲は狭くなるので、正則化の値は大きくなり、$w$は事前分布の平均に収束していきます。
その様子を見てみましょう。
$D=4$ , $alpha=1$
最尤推定では4次元で過学習を起こしてるっぽかったですが、$α=1$のMAP推定だとそこは大丈夫そうですね!
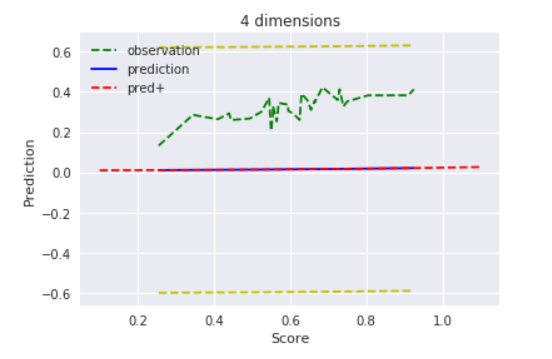
$D=4$ , $alpha=0.001$
$alpha=0.001$の時は分散がかなり小さいので、値はほぼ平均$0$とと考えて良いでしょう。その為、観測データすら無視して平均に収束しています。
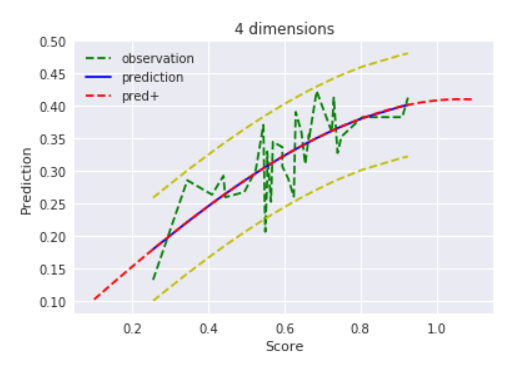
$D=4$ , $alpha=1000$
逆に$alpha=1000$の時は分散が大きいので、正則化がないに等しい=最尤推定と同様の結果になる、、と思ったのですが、そうでもありませんね。
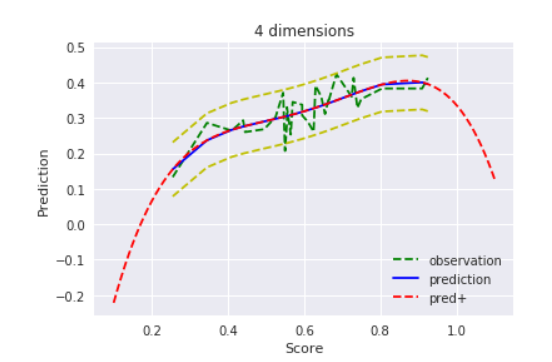
$D=4$ , $alpha=1000000$
事前分布の分散を100万まで上げて、やっと最尤推定と同じような結果になってくれました。
MAP推定、ないし正則化の力は確かですね!
ただ、、、本末転倒ですがそもそも元のデータが曲線フィッティングに適していないんじゃないかと思い、ここでも念のためsin波で試してみましたw
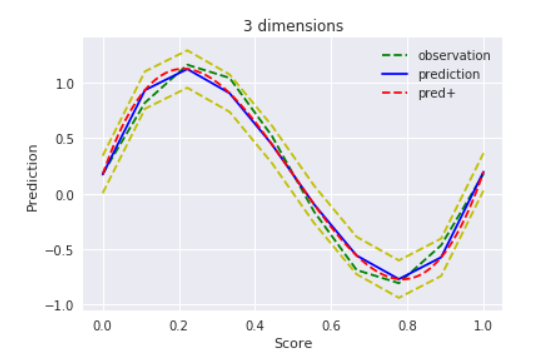
$D=3$ , $alpha=1$
どうやら、$α=1$だと正則化が強すぎるみたいですね。。$α=100$でもまだフィッティングしてくれず、
$D=3$ , $alpha=10000$
$α=10000$でやっとフィッティングしてくれました。
MAP推定を使う時は、事前分布の値を適切に与えてあげないと、おかしな結果になってしまいますね。ここは試行錯誤するしかないな。
ベイズ推定
ベイズ推定は現在別記事でPyStanを使い実施中なので、興味あったら見てみてください。
Python(PyStan)で「StanとRでベイズ統計モデリング」の4節をやってみた
【PythonとStanで重回帰】「StanとRでベイズ統計モデリング」の5.1節をやってみた(PyStan)
以上です。冗長な部分が多いかもしれませんが、参考になれば。
間違いやご指摘などありましたらご遠慮なくコメント頂けますと幸いです。