活性化関数ReLUについてとReLU一族【追記あり】

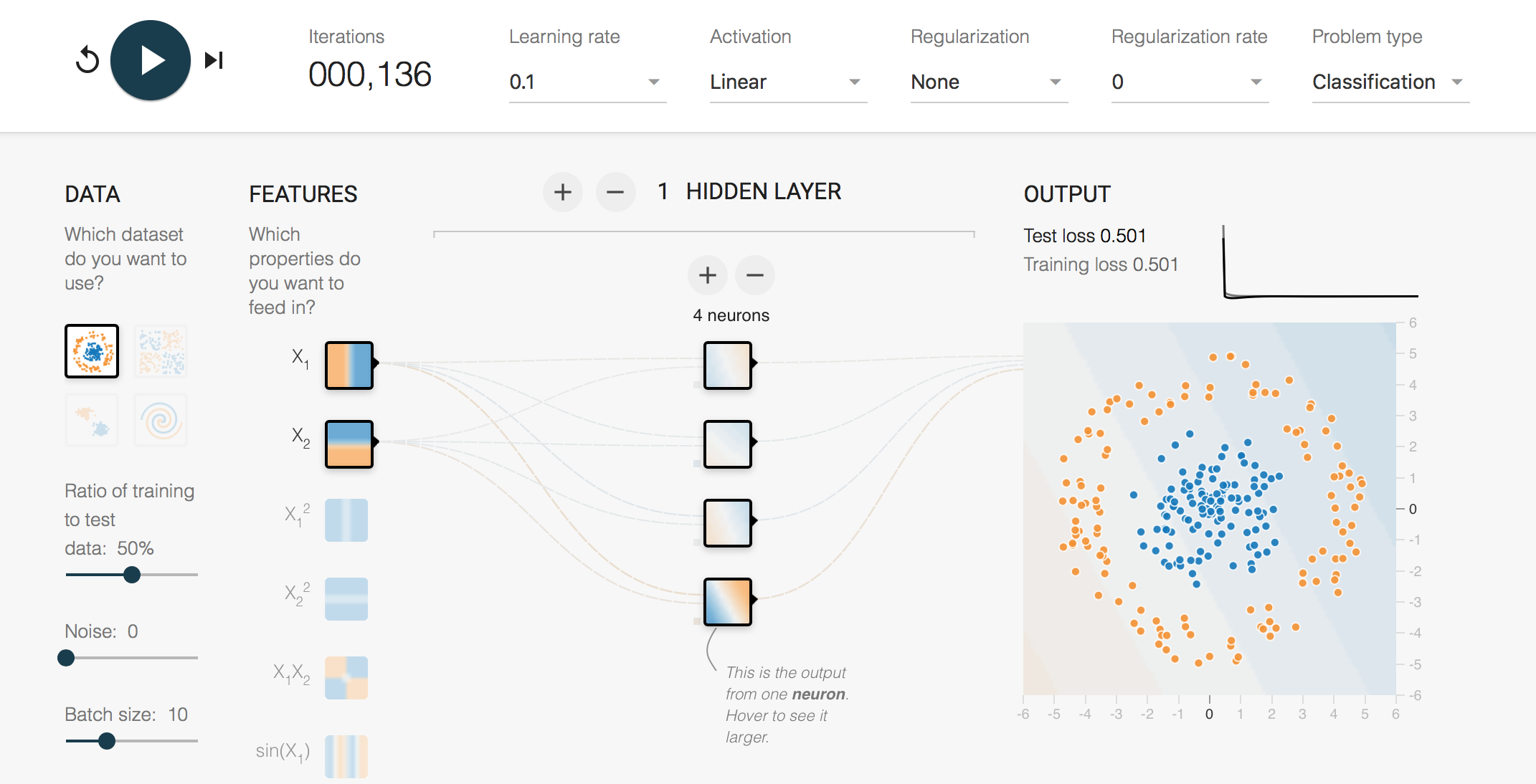
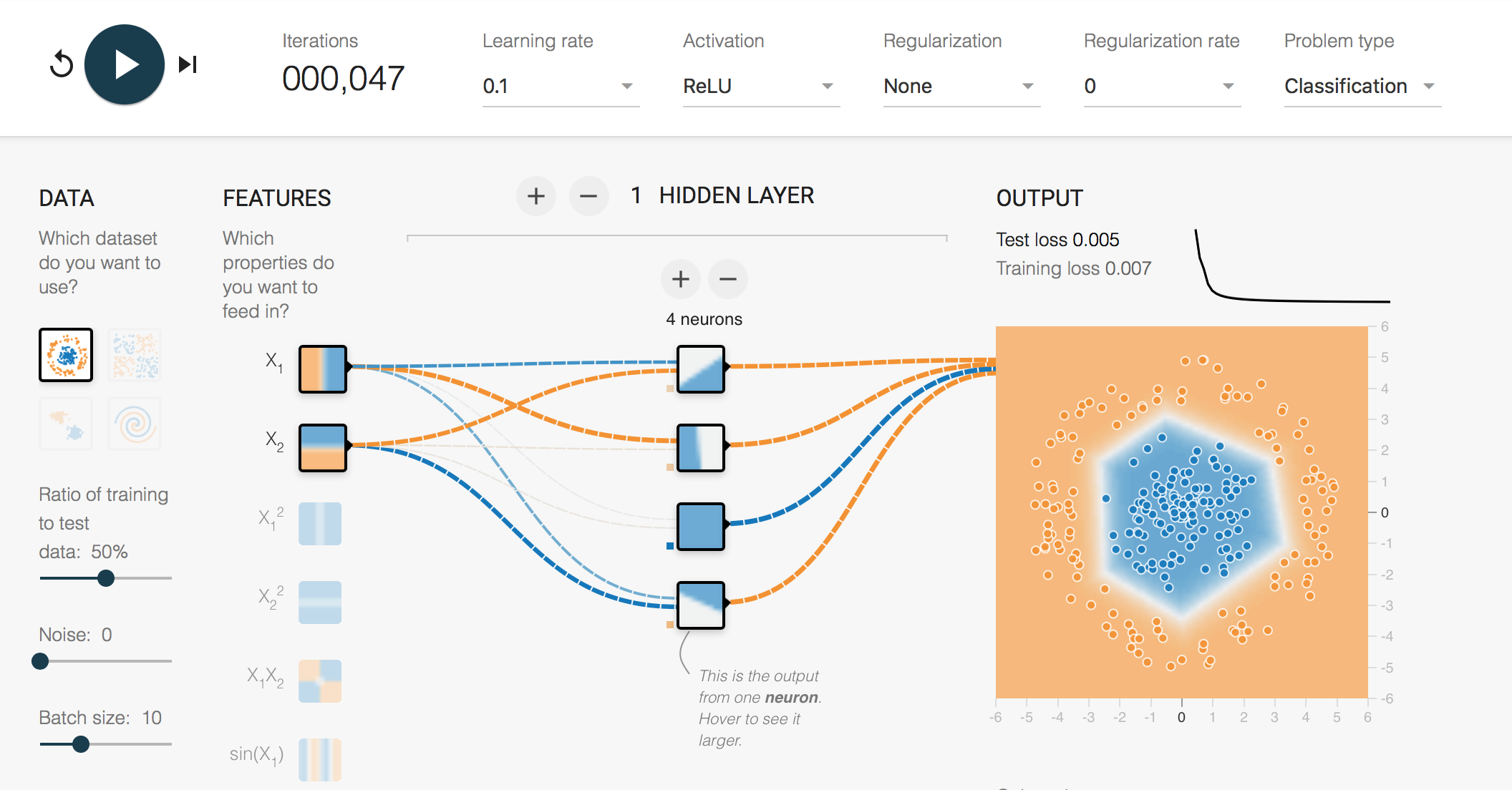
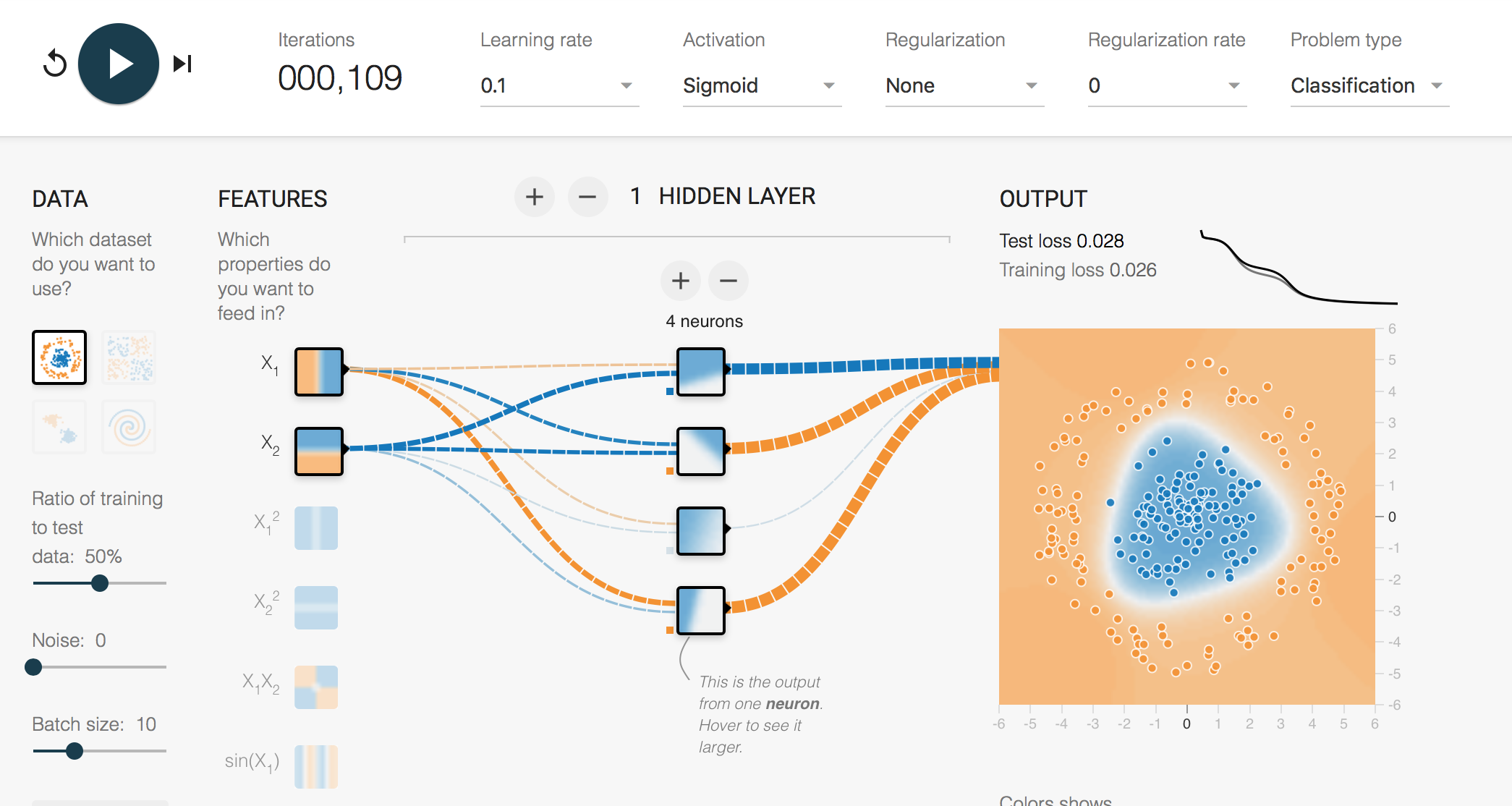
(追記)活性化関数が学習に及ぼす影響

下記記事にて実験&解説を実施。興味があれば是非。

【ReLU, PReLU, シグモイド etc...】ニューラルネットでよく使う活性化関数の効果をKerasで調べてみた

ReLUの良さ

• $\max(0,x)$は単純ゆえに早い
• 0を作る→スパース性につながる
• $x>0$の部分では微分値が常に1であるため勾配消失の心配はない

ReLUが活性化関数になれる理由

折れ線のようなグラフで近似ができる

wikipediaの最後に，$y=x^2$の近似が載ってる

[wikipedia 活性化関数] (https://ja.wikipedia.org/wiki/活性化関数)

\phi=\max(0,x)

y\simeq$2\phi(-x - 2) + 2\phi(-x - 1) + \phi(-x) + \phi(x) + 2\phi(x - 1) + 2\phi(x - 2)

google play groundで見ると面白い Link

中間層からの振る舞いを見ると面白い

確かにReLUは折れ線を組み合わせている感じ．

多分各層の数の積の多角形が作れる

• Linear
  

• ReLU
  

• sigmoid
  

ReLU一族

ReLU

$$f = \max(0,x)$$

• 参考(PFN得居さんの資料) : 最適化から見たディープラーニングの考え方

近似関数

$$f = log(1+e^x)$$

Leaky ReLU

最近よく使われている(wikipedia曰く無意味らしいが...)

(wikipedia)
2013年に max(0.01x, x) が LReL (leaky rectified linear) と命名された。ただし、命名者はこの活性化関数を使う意味はなかったと報告している。

f = \begin{cases}
    x & (x>0) 
    \\
    0.01x  & (x<=0)
  \end{cases}

Parametric ReLU

ReLUの傾きをparametricにした

f = \begin{cases}
    x & (x>0) 
    \\
    ax  & (x<=0)
  \end{cases}

• 参考(原著) : Delving Deep into Rectifiers:Surpassing Human-Level Performance on ImageNet Classification

Exponential Linear Units

f = \begin{cases}
    x & (x>0) 
    \\
    e^x -1  & (x<=0)
  \end{cases}

• 参考(原著) : Fast and Accurate Deep Network Learning by Exponential Linear Units

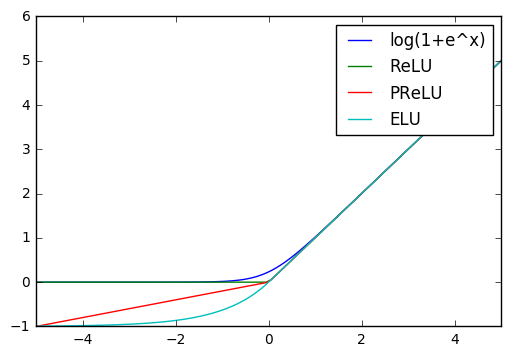
図示

ReLU一族図示

0付近が微妙に異なる模様