はじめに
最近は今までライブラリに頼ってブラックボックス化していたものを、一つずつでもなくせるように色々と実装しています。前回はSGDによるロジスティック回帰を、今回は正則化・近接勾配法を実装したので備忘録程度にまとめました。
近接勾配法
機械学習などでは目的関数を最小化する作業があります。そして、関数の最小化と言えば「微分」です。もし、目的関数が微分可能であれば勾配降下法(SGDなど)が使用できます。しかし、(部分的に)微分できない目的関数も存在します。そのような時は近接勾配法が利用できます。近接勾配法は式の導入こそややこしくはありますが、実際にプログラムするところは簡単で、勾配降下法の更新式にProximal Operatorという項を掛け合わせるだけです。
再度、ロジスティック回帰を例にあげながら説明します。
- 目的関数L=f(w)が微分可能であるとき
ロジスティック回帰で言うところのF(w)は、以下のようになります。
L = f(w) = - \sum_{n=1}^{N}\ln\{s(x_n)^{y_n}(1 - s(x_n))^{1-y_n}\}\\
s() : シグモイド関数\\
x : 説明変数\\
y : 正解ラベル(0, 1)
この場合の重みwの更新式は勾配降下法により以下のようになります。
w \leftarrow w - \eta\frac{\partial L}{\partial w}
- 目的関数L=f(w)+g(w)が(部分的に)微分できないとき
例えば、以下に示すようなL1正則化ロジスティック回帰の目的関数です。
L = f(w) + g(w)\\
= - \sum_{n=1}^{N}\ln\{s(x_n)^{y_n}(1 - s(x_n))^{1-y_n}\} + \lambda \| w \|_1\\
※ g(w) = \lambda \| w \|_1\\
L1正則化の罰則項であるg(w)はw=0のところで連続ではないので微分できません
このように、目的関数の中に(部分的に)微分できないg(w)のような項を含む場合は近接勾配法を利用します。
近接勾配法による重みwの更新式は以下のようになります。
w \leftarrow prox_{\gamma g}(w - \eta\frac{\partial L}{\partial w})\\
※ prox_{\gamma g} : Proximal Operator
勾配降下法との違いは勾配にProximal Operatorという変数が掛け合わされているだけです。Proximal Operatorについては次章で紹介します。
ここまでで一旦、近接勾配法によるロジスティック回帰の枠組みをプログラムします。
# 近接勾配法
def proximal_gradient(grad_f, prox, gamma, objective, init_w, tol = 1e-6):
w = init_w
result = objective(w)
while 1:
w_new = prox(w - gamma * grad_f(w), gamma)
result_new = objective(w_new)
# 停止条件を説明変数差分のノルムに
if np.linalg.norm(w_new - w, 2) < tol:
break;
w = w_new
result = result_new
return w_new, result_new
# X:学習用データベクトルを列ベクトルとして並べた行列
# y:ラベルを並べたベクトル
def LogisticRegression(X, y, lam):
# ロジスティック回帰内部の計算
sigma = lambda a : 1.0/(1.0+np.exp(-a))
p=lambda Z, w:sigma(np.dot(Z.T, w))
X=np.concatenate((np.ones((1,np.size(X,1))), X), 0) #バイアス項の追加
# 勾配
grad_E = lambda w: np.dot(X, p(X, w) - y)
(u, l, v) = np.linalg.svd(X)
gamma = 1.0/max(l.real*l.real)
# 目的関数
objective = lambda w: - np.sum( y * np.log(p(X, w)) + \
(1 - y) *np.log(( 1 - p(X, w)))) + \
l1_norm(lam, w) # <= 正則化手法に応じて変更(次の章で紹介)
# l1_norm(lam, w)
# l2_norm(lam, w)
# elastic_norm(lam, w)
# group_norm(lam, w)
# proximal operator
prox = lambda w, gamma:prox_l1(w, gamma, lam) # <= 正則化手法に応じて変更(次の章で紹介)
# prox_l1(w, gamma, lam)
# prox_l2(w, gamma, lam)
# prox_elastic(w, gamma, lam)
# prox_group(w, gamma, lam)
# 近接勾配法
w_init = np.zeros(X.shape[0])
(w_hat, result) = proximal_gradient(grad_E, prox, gamma, objective, w_init, 1e-6)
return w_hat, result
各種Proximal Operator
Proximal Operatorは正則化項のようなg(x)を使って計算されるパラメータで、式による導入が可能です(詳細)。以下に、一般的に使用される正則化項g(w)とそのProximal Operatorを紹介します。加えて、それらを計算する関数も載せています。
L1正則化
L1正則化は意味のない説明変数の重みwがゼロになりやすいという特徴を持ち、過学習を抑える。よって、「不要なパラメータを削りたい」・「変数選択したい」という時によく使われる。なお、L1正則化はLassoとも呼ばれる。
g(w) = \lambda \| w \|_1\\
prox_{\gamma g}(w) = S_{\gamma \lambda}(w) = \left\{
\begin{array}{ll}
w_i - \gamma \lambda & (w_i \geq \gamma \lambda) \\
0 & (- \gamma \lambda \lt 0 \lt \gamma \lambda) \\
w_i + \gamma \lambda & (w_i \leq \gamma \lambda)
\end{array}
\right.
def l1_norm(lam, w):
penalty = lam * np.sum(np.abs(w))
return penalty
def prox_l1(w, gamma, lam):
prox = np.zeros(w.shape[0])
thresh = gamma * lam
prox[w >= thresh] = w[w >= thresh] - thresh
prox[w <= -thresh] = w[w <= -thresh] + thresh
return prox
L2正則化
L2正則化はL1正則化ほど極端ではないが(重みwがゼロになりやすいわけではないが)、過学習を抑えて汎化された滑らかなモデルを得やすくなる。なお、L2正則化はRidgeとも呼ばれる。
g(w) = \lambda \| w \|_2 \\
prox_{\gamma g}(w) = \frac{1}{1 + 2 \gamma \lambda}w
def l2_norm(lam, w):
penalty = lam * np.sum(np.abs(w**2))
return penalty
def prox_l2(w, gamma, lam):
prox = w/(1+2*gamma*lam)
return prox
Elastic Net
Elastic NetはL1正則化とL2正則化を組み合わせた正則化手法です。
g(w) = \lambda_1 \| w \|_1 + \lambda_2 \| w \|_2 \\
prox_{\gamma g}(w) = \frac{1}{1 + 2 \gamma \lambda_2}S_{\gamma \lambda_1}(w)
def elastic_norm(lam, w):
lam1 = lam[0]
lam2 = lam[1]
penalty = l1_norm(lam1, w) + l2_norm(lam2, w)
return penalty
def prox_elastic(w, gamma, lam):
lam1 = lam[0]
lam2 = lam[1]
Sv = prox_l1(w, gamma, lam1)
prox = Sv/(1+2*gamma*lam2)
return prox
Group Lasso(重複あり)
Group Lassoは説明変数がいくつかのグループに分けられる時に、グループごとに正則化を行う手法です(重みベクトルwのうちグループgに属する変数を並べたのがwg)。これにより、グループごとにスパースになる・ならないが決まります。そして、以下はグループ間で説明変数の重複がない場合です。
g(w) = \lambda \sum_{g \in G} \| w_g \|_2 \\
prox_{\gamma g}(w) = \left\{
\begin{array}{ll}
w_g - \gamma \lambda \frac{w_g}{\| w_g \|_2} & (\| w_g \|_2 \geq \gamma \lambda) \\
0 & (\| w_g \|_2 \leq \gamma \lambda)
\end{array}
\right.
def group_norm(lam, w):
penalty = 0
for i in group_list:
group_index = np.where(group_ids == i)
penalty += np.sum(np.abs(w[group_index]**2))
return lam * penalty
def prox_group(w, gamma, lam):
# group_ids と group_list は事前に定義して、
# グローバル変数として使っています。
prox = np.zeros(w.shape[0])
thresh = gamma * lam
for i in group_list:
group_index = np.where(group_ids == i)
group_l2 = np.sum(np.abs(w[group_index]**2))
if group_l2 > thresh:
prox[group_index] = w[group_index] - gamma*lam*w[group_index]/group_l2
return prox
ちなみに、グループ間で重複がある場合のGroup Lassoも提案されているようですがまだ追えていません。だれか、Proximal Operatorを求めていないでしょうか???
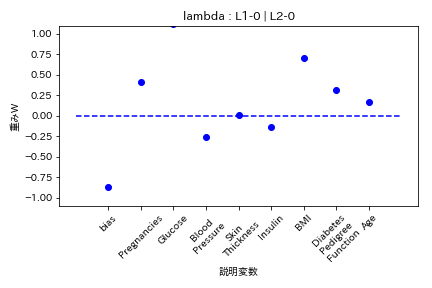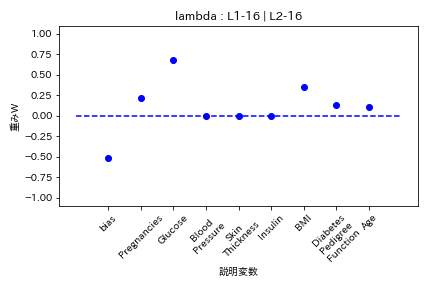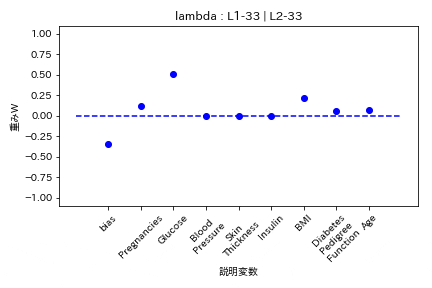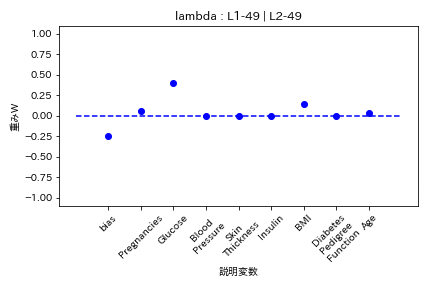
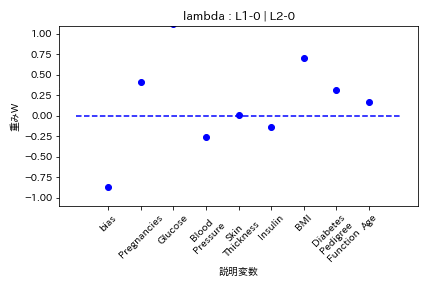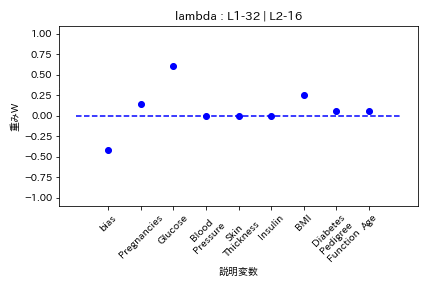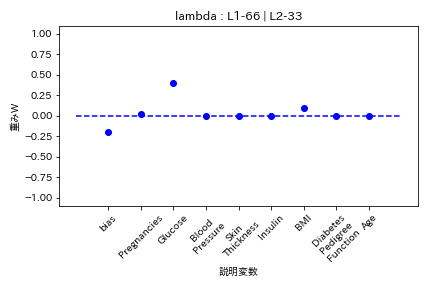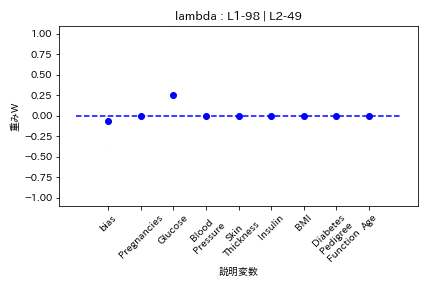
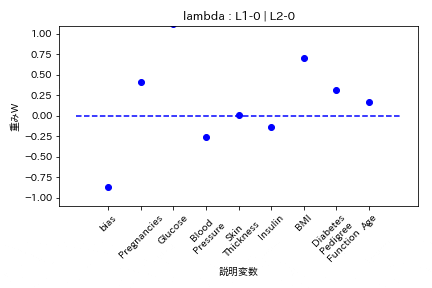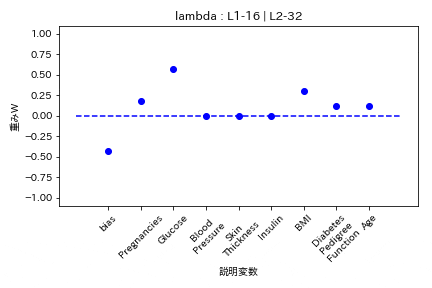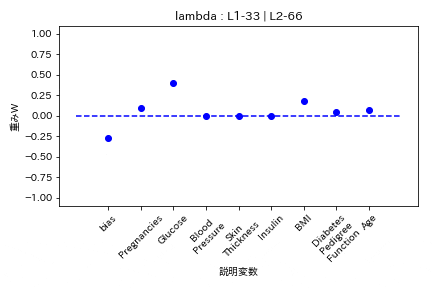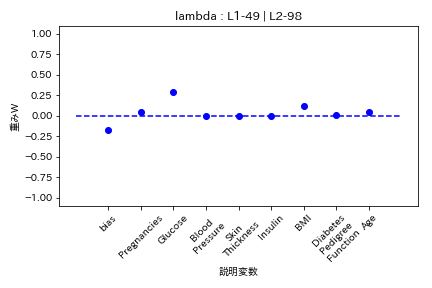
実験結果
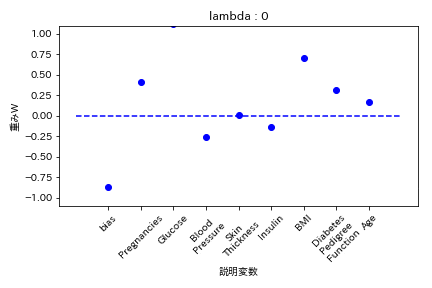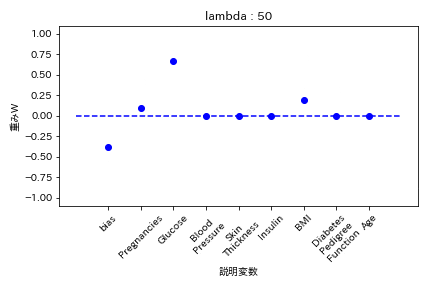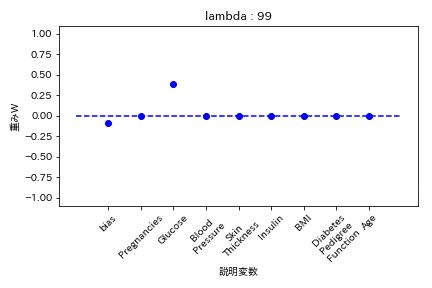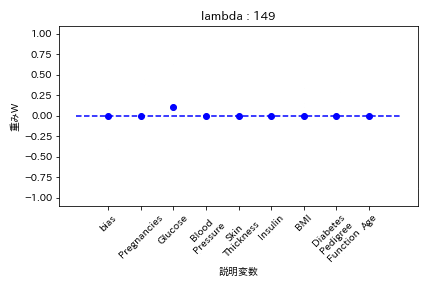
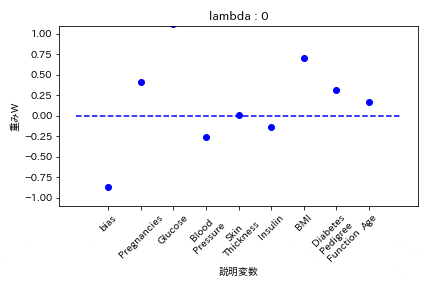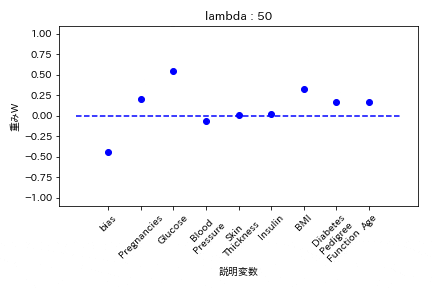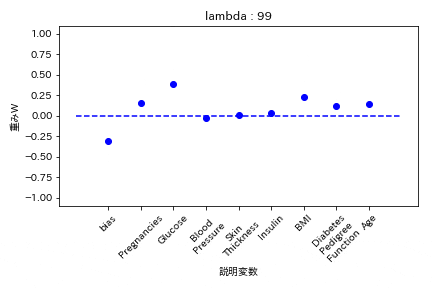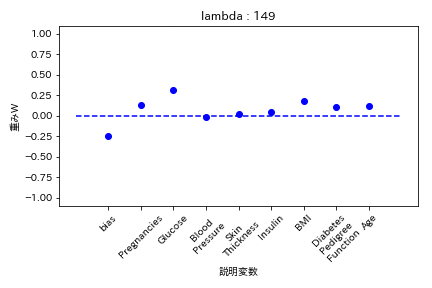
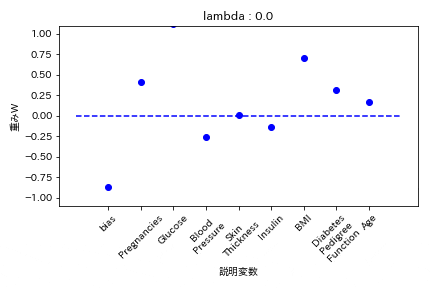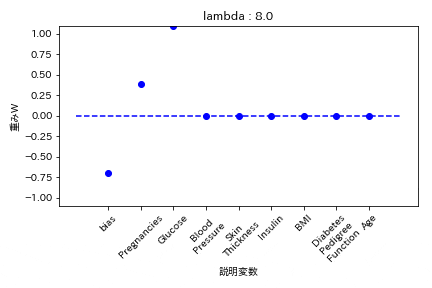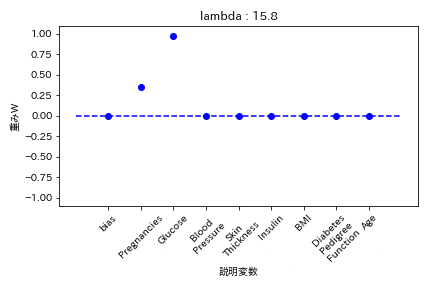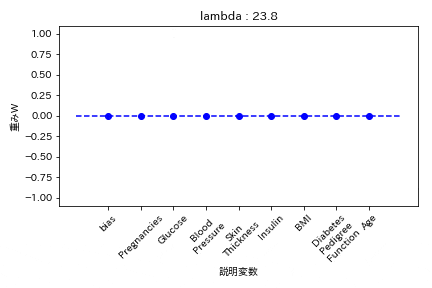
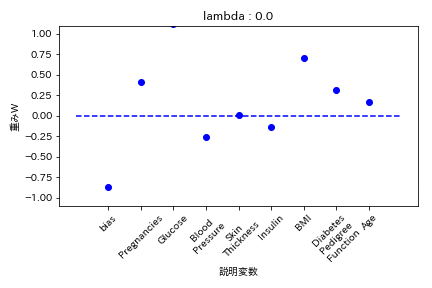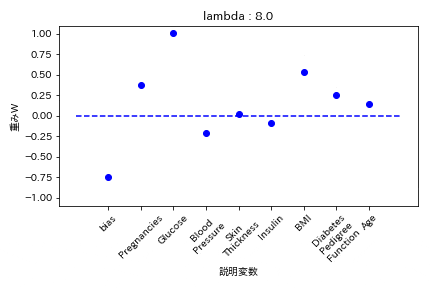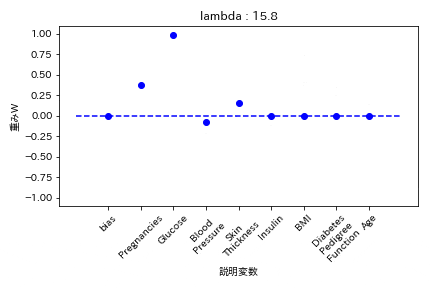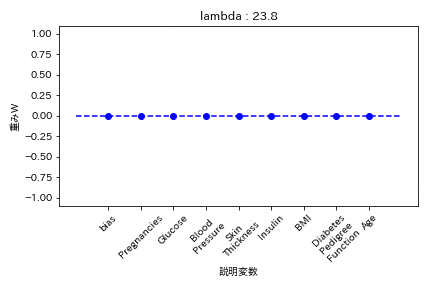
糖尿病患者のデータセットを用いて糖尿病かどうかを学習する際の重みWの挙動を可視化した。
- Regularization-ProximalOperator : 一連のプログラム
L1正則化
重みが完全に0になる。
L2正則化
L1ほど重みが0になりにくい。
Elastic Net
- L1ラムダとL2ラムダが同じ割合
- L1ラムダがL2ラムダの2倍
L1の方が強く効くので重みがゼロになりやすい。
- L2ラムダがL1ラムダの2倍
L2の方が強く効く。
Group Lasso
グループごとに重みがゼロになる。
- グループの分け方
- [bias]
- [Pregnancies, Glucose]
- [Blood~, Skin~]
- [Insulin, BMI]
- [Diabetes~, Age]
- グループの分け方
- [bias]
- [Pregnancies, Glucose, Blood~, Skin~]
- [Insulin, BMI, Diabetes~, Age]